ГИДРОСТАТИКА Гидростатическое давление и его свойство Гидростатикой

ГИДРОСТАТИКА Гидростатическое давление и его свойство

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практические приложения. Жидкости практически не способны сопротивляться растяжению, а в неподвижных жидкостях не действуют касательные силы. Поэтому на неподвижную жидкость из поверхностных сил могут действовать только силы давления; причем на внешней поверхности рассматриваемого объема жидкости силы давления всегда направлены по нормали внутрь объема жидкости и, следовательно, являются сжимающими.

Под внешней поверхностью жидкости понимают не только поверхность раздела жидкости с газообразной средой пли твердыми стенками, но и поверхность объема, мысленно выделяемого из общего объема жидкости. Таким образом, в неподвижной жидкости возможен лишь один вид напряжения — напряжение сжатия, т. е. гидростатическое давление.

Основное свойство гидростатического давления: в любой точке жидкости гидростатическое давление не зависит от ориентировки площадки, на которую оно действует, т. е. от углов ее наклона по отношению к координатным осям.

Рис. Схема для доказательства свойства гидростатического давления

Для доказательства выделим в неподвижной жидкости элементарный объем в форме тетраэдра с ребрами, параллельными координатным осям и соответственно равными dx, dy и dz (рис. ). Пусть внутри выделенного объема на жидкость действует единичная массовая сила, составляющие которой равны X, Y и Z. Обозначим через рх гидростатическое давление, действующее на грань, нормальную к оси Ох, через ру — давление на грань, нормальную к оси Оy, и т. д. Гидростатическое давление, действующее на наклонную грань, обозначим через рп, а

Cоставим уравнение равновесия выделенного объема жидкости в направлении оси Ох, учитывая, что все силы направлены по нормалям к соответствующим площадкам внутрь объема жидкости. Проекция сил давления на ось Ох pxdydz/2 – pпd. S cos (п, x). Масса жидкости в тетраэдре равна произведению ее объема на плотность, т. е. dxdydz ρ/6, следовательно, массовая сила, действующая на тетраэдр вдоль оси Ох, составляет dx dy dzρX/6.

Уравнение равновесия тетраэдра: dy dz px/2 - рп d. S cos (n, x)+ +dx dy dz ρX/6= 0. Разделив это уравнение на площадь dydz/2, которая равна площади проекции наклонной грани d. S на плоскость y. Oz, т. е. dydz/2 = d. S cos (n, x ), получим px - pп + dx. Xρ/3 =0.

При стремлении размеров тетраэдра к нулю последний член уравнения (dx. Xρ/3) содержащий множитель dx, также стремится к нулю, а давления рх и рп остаются величинами конечными. Следовательно, в пределе получим px - pп = 0 или px = pп.

Аналогично из уравнений равновесия вдоль осей Оу и Oz, находится py = pп , pz = pп или px=py=pz=pп. (1. 21) Так как размеры тетраэдра dx, dy и dz взяты произвольно, то и наклон площадки d. S произволен и, следовательно, в пределе при стягивании тетраэдра в точку давление в этой точке по всем направлениям будет одинаково.

Основное уравнение гидростатики– уравнение для нахождения гидростатического давления в любой точке рассматриваемого объема жидкости. Рассмотрим частный случай равновесия жидкости: на нее действует одна массовая сила — сила тяжести. Если объем жидкости весьма мал по сравнению с объемом Земли, то свободную поверхность жидкости можно считать горизонтальной плоскостью.

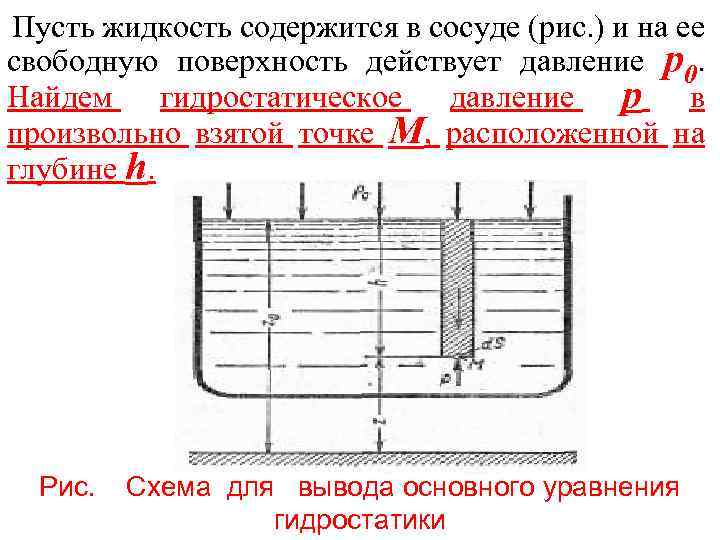Пусть жидкость содержится в сосуде (рис. ) и на ее свободную поверхность действует давление р0. Найдем гидростатическое давление р в произвольно взятой точке М, расположенной на глубине h. Рис. Схема для вывода основного уравнения гидростатики

Выделим около точки М элементарную горизонтальную площадку d. S и построим на ней вертикальный цилиндрический объем высотой h. Условие равновесия этого объема жидкости. Сумма сил, действующих на рассматриваемый объем в проекции на вертикаль: pd. S - p 0 d. S - ρgh d. S = 0. (Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т. е. вверх. ) Последний член уравнения (ρgh d. S ) представляет собой вес жидкости в указанном объеме. Силы давления по боковой поверхности цилиндра в уравнение не входят, так как они нормальны к вертикали. Сократив выражение на d. S и перегруппировав члены, получим р = р0 + hρg = p 0 + hγ. (1. 22)

Уравнение (р=р0+hρg=p 0+hγ) - основное уравнение гидростатики - по нему можно подсчитать давление в любой точке покоящейся жидкости. Это давление складывается из: давления р0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости. Величина p 0 является одинаковой для всех точек объема жидкости, поэтому, учитывая свойство гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково. Это закон Паскаля. Давление жидкости по формуле (1. 22), возрастает с увеличением глубины по закону прямой и на данной глубине есть величина постоянная.

Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня. В данном случае поверхностями уровня являются горизонтальные плоскости, а свободная поверхность является одной из поверхностей уровня.

Обозначив через z координату точки М, через z 0 — координату свободной поверхности жидкости и заменив в уравнении (1. 20 - р = р0 + hρg = p 0 + hγ) h на z 0 - z, получим z+p/(ρg)=z 0+p 0/(ρg). (1. 23) Так как точка М взята произвольно, то и для всего рассматриваемого неподвижного объема жидкости z + p/(ρg) = const.

Координата z - геометрическая высота (имеет линейную размерность). Величина p/(ρg) - пьезометрическая высота (имеет линейную размерность). z+p/(ρg) - гидростатический напор (имеет линейную размерность). Таким образец, гидростатический напор есть величина постоянная для всего объема неподвижной жидкости. Те же результаты можно получить путем интегрирования дифференциальных уравнений равновесия жидкости.