Гидромеханика проф. , д. ф. м. н. С. А. Ермаков
Литература: - Войткунский Я. И. , Фаддеев Ю. И. , Федяевский К. К. Гидромеханика. 1982 г. - Альтшуль А. Д. , Животовский Л. С. , Иванов Л. П. Гидравлика и аэродинамика. М. Стройиздат. 1987 г. - Луговский В. В. Гидромеханика. Учебное пособие. 1990 г. - Фейнман Р. , Лейтон Р. Сэндс М. Фейнмановские лекции по физике. Т. 7. гл. 40, 41. - Алферьев М. Я. Гидромеханика. 1961 г. - Справочник по теории корабля. Войткунский Я. И. 1985 т. 1.
Описание состояния жидкости Описание состояния и движения жидкости (газа) основано на модели сплошной среды: - вещество непрерывным образом распределено в жидкости - все характеристики среды описываются непрерывными функциями координат в пространстве. Состояние жидкости описывается полями - вектора скорости u=u(x, y, z, t)=(ux, uy, uz)=(u, υ, w) - давления p=p(x, y, z, t) - плотности ρ=ρ(x, y, z, t)
Силы, действующие в жидкости 1. Массовые (объемные) силы- это силы, приложенные к жидкой частице и пропорциональные ее массе - массовая сила, действующая на жидкость в объеме V напряжение массовых сил, т. е. сила, действующая на единицу массы жидкости. - Пример массовой силы – сила тяжести
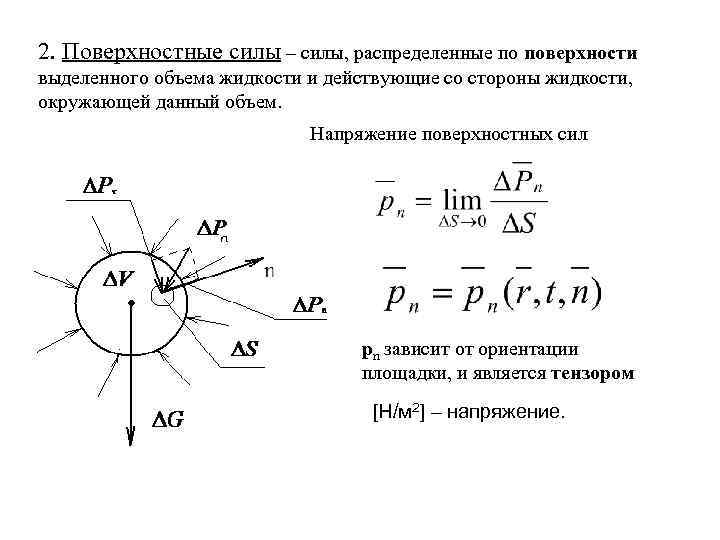2. Поверхностные силы – силы, распределенные по поверхности выделенного объема жидкости и действующие со стороны жидкости, окружающей данный объем. Напряжение поверхностных сил pn зависит от ориентации площадки, и является тензором [Н/м 2] – напряжение.
Тензор поверхностных напряжений в жидкости z k i x j y pij – напряжение, действующее на площадку оси i в направлении оси j
Тангенциальные напряжения в жидкости Тангенциальные напряжения возникают в вязкой движущейся жидкости Сила трения при плоско-параллельном течении согласно гипотезе Ньютона: µ – коэффициент динамической вязкости - градиент скорости или скорость угловой деформации
Общий вид тензора тангенциальных напряжений (несжимаемая жидкость) Почему? Данная форма напряжений удовлетворяет условию ij=0 при равномерном вращении жидкости как целого. Доказательство. (2 -мерное движение жидкости) y u r z water t θ=ωt x
Нормальные напряжения в вязкой жидкости Нормальные напряжения представляем в виде давления в невязкой жидкости и слагаемых с вязкостью, при этом полагаем их зависящими только от производной скорости по соотв. нормальным координатам Среднее от нормальных напряжений по 3 направлениям в несжимаемой жидкости равно давлению в невязкой жидкости.
