Гидродинамика Солнца Лекция 1 Солнечная грануляция granulation

Гидродинамика Солнца Лекция 1

Солнечная грануляция (granulation)

Солнечный ветер и корональные выбросы массы

Корональный выброс массы (coronal mass ejection)

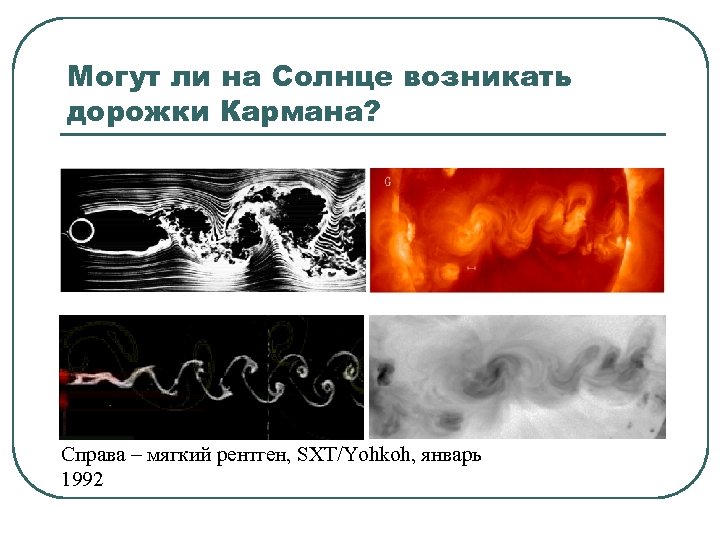Могут ли на Солнце возникать дорожки Кармана? Справа – мягкий рентген, SXT/Yohkoh, январь 1992

Основные характеристики Солнца Спектр. класс G 2 1 а. е. = 1. 496 × 1013 см = = 214. 9 r m = 1. 989 × 1033 г Угл. радиус = 959. 63″ 1″ в центре диска соответствует 710– 734 км r = 6. 96 × 1010 см = = 109 r. E g = 2. 74 × 104 см/с2 (на поверхности) L = 3. 84 × 1033 эрг/с M = 4. 74 m (10 пс) Teff = 5780 K Tc = 1. 6 × 107 K

Основные характеристики Солнца Состав (%% полной массы): водород ― 68%, гелий ― 30%, остальные элементы ― 2% Средняя плотность вещества 1. 41 г/см 3, в центре 1. 6 × 102 г/см 3

Основные черты внутреннего строения Солнца

Термоядерные реакции в центральной части Солнца: водородный и углеродно-азотный циклы

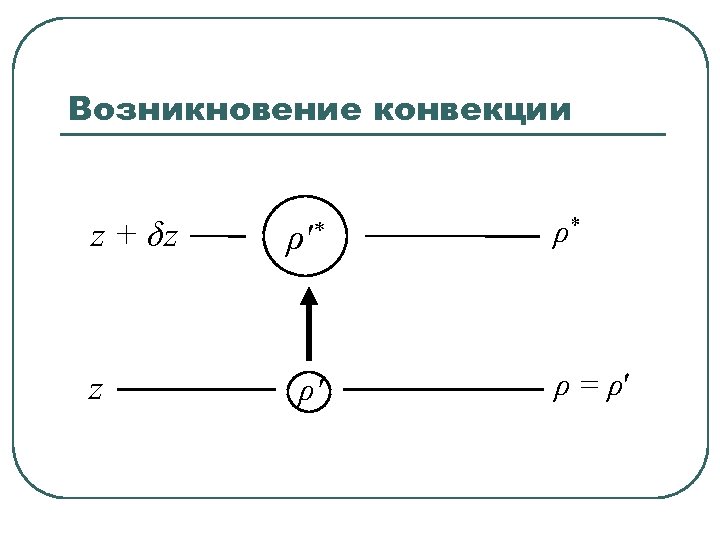Возникновение конвекции z + δz z ρ′* ρ′ ρ* ρ = ρ′

Возникновение конвекции Условие неустойчивости: или Уравнение состояния: При условии баланса давлений (p′* = p*) и μ = const:

Возникновение конвекции Условие (критерий) К. Шварцшильда (1906): Показать самостоятельно, что вариации μ не влияют на вид условия Шварцшильда

(Необходимое) условие конвективной неустойчивости Обозначим Поскольку где ― высота однородной атмосферы (шкала высот ― scale height) для давления ( ), то Другая запись условия Шварцшильда: Ñ > Ñad

Безразмерный изэнтропический градиент температуры Адиабатический процесс:

Лучистая теплопроводность (radiative thermal conductivity) (κ – усредненный по Росселанду коэффициент поглощения на единицу массы) Лучистая температуропроводность (radiative thermal diffusivity):

Двоякая роль частичной ионизации l увеличение теплоемкости, уменьшение γ и cp cv γ l уменьшение прозрачности и χR, увеличение Области частичной ионизации конвективно наиболее неустойчивы

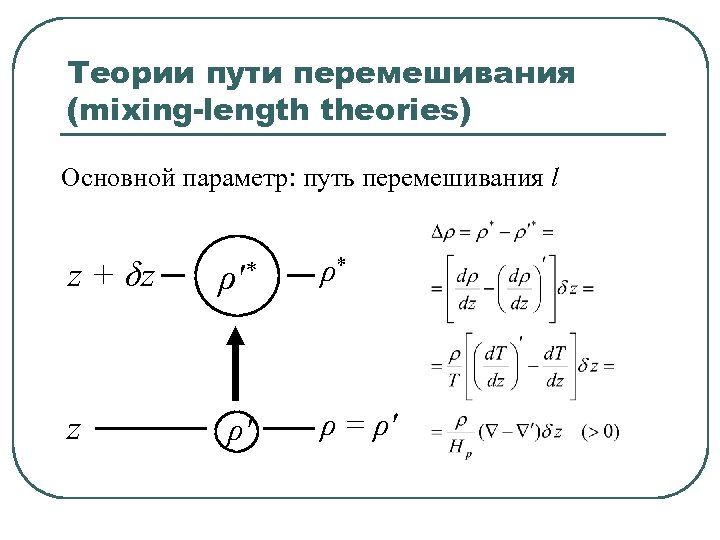Теории пути перемешивания (mixing-length theories) Основной параметр: путь перемешивания l z + δz ρ′* ρ* z ρ′ ρ = ρ′

Вычисление скорости элемента (parcel) в конце пути перемешивания В верхней точке отрезка (z, z + δz):

Вычисление средней конвективной скорости Учет потерь на трение: множитель Полагаем для среднего v (по многим элементам) Стандартное допущение: l = αHp

Конвективный поток энергии (convective energy flux) Принимаем Конвективный поток:

Уравнение сохранения полного потока энергии FR + FC = L /4πr 2 = Лучистый поток (в приближении лучистой теплопроводности – radiative heat conduction): [χR – лучистая температуропроводность (radiative thermal diffusivity); κ – коэффициент поглощения (opacity coefficient), рассчитанный на единичную массу] Конвективный поток:

Учет неадиабатичности теплового режима всплывающего объема Считаем, что конвективный поток энергии уменьшен по сравнению со случаем адиабатичности на величину отдачи тепла всплывающими элементами окружающей среде Плотность лучистого потока через поверхность всплывающего объема (d – его линейный размер):

Учет неадиабатичности теплового режима всплывающего объема Представляем конвективный поток в виде Приравниваем f. R S = ΔFC q (S – площадь поверхности объема, q – его поперечное сечение):

Учет неадиабатичности теплового режима всплывающего объема

Уравнения модели конвективной зоны L /4πr 2 – известные функции T и ρ)

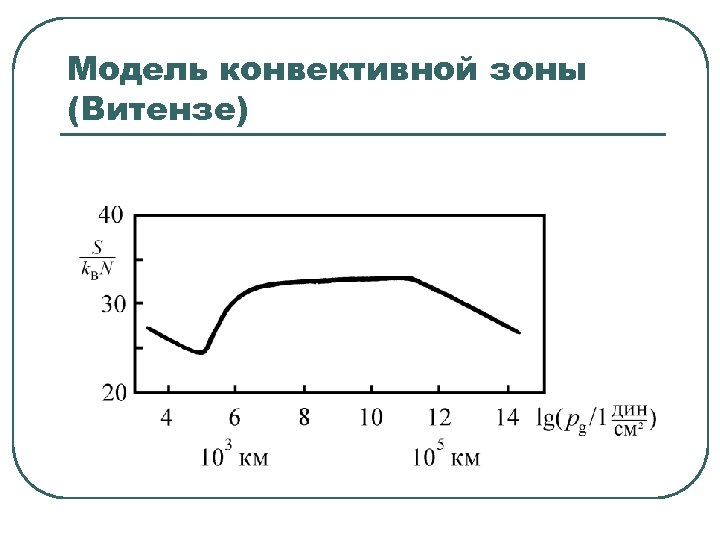Модель конвективной зоны (Витензе)

Структурная организация солнечной конвекции

Солнечная грануляция

Солнечная грануляция Открыта Гершелем (Herschel) в 1801 г. Обнаружение многоугольной формы ячеек – Strebel (1933) Unsöld (1930) связал грануляцию с конвекцией Две альтернативные интерпретации: l Siedentopf (1933) – горячие газовые объемы l Plaskett (1936) – конвективные ячейки

Хромосферная сетка – отпечаток супергрануляционной структуры

Допплерограмма, выявляющая супергрануляционную структуру

Супергрануляция Обнаружение: Leighton et al. (1962), метод допплеровской спектрогелиографии Горизонтальный размер супергранул ~ 30 Мм Гелиосейсмологические данные (MDI на SOHO): супергрануляционные течения тянутся вглубь на 8 Мм Горизонтальные скорости 200– 500 м/с Скорости восходящих течений в центре 50– 100 м/с, нисходящих по краям 100– 200 м/с Время жизни: у большинства 15– 30 ч, иногда 2 сут и более ― до 4 сут

Мезогрануляция Обнаружение: November et al. (1981), метод допплеровской спектрогелиографии Дальнейшее подтверждение: метод локального корреляционного трассирования (local correlation tracking)

Гигантские ячейки Simon & Weiss (1968) теоретически предсказали существование 3 или 4 масштабов ячеек (реально наблюдались 2) Bumba с конца 60 -х гг. неоднократно отмечал признаки гигантских ячеек в распределении фоновых магнитных полей Первые прямые наблюдения ― Beck et al. (1998): размеры ячеек 40– 50° долготы и < 10° широты

Литература l M. Stix. The Sun. An Introduction. 2 nd Ed. Berlin: Springer, 2002. l С. А. Каплан, С. Б. Пикельнер, В. Н. Цытович. Физика плазмы солнечной атмосферы. М. : Физматлит, 1977. l P. N. Brandt. Solar Photosphere: Granulation. Encycl. Astron. Astrophys. , 2001. l R. Stein. Solar Photosphere: Mesogranulation. Encycl. Astron. Astrophys. , 2001. l G. Simon. Solar Photosphere: Supergranulation. Encycl. Astron. Astrophys. , 2001.

Александр Владимирович Гетлинг Тел. дом. ≡ раб. : 433 -74 -45 моб: 8 (903) 505 -18 -46 Эл. почта: A. Getling@mail. ru Веб-страница: www. magnetosphere. ru/~avg