Гидравлика специальность АДи А Пояснение к решению задач

Гидравлика (специальность АДи. А) Пояснение к решению задач по равномерному и неравномерному движению

Тема: Истечение жидкости через насадки Насадком называют короткую трубу, присоединённую к отверстию в тонкой стенке. Длина насадка равна трём – пяти диаметрам отверстия. По форме насадок может быть: внешним цилиндрическим, внутренним цилиндрическим, коническим сходящимся, коническим расходящимся, коноидальным.

Наиболее частыми задачами при расчётах истечения жидкости из насадков являются : 1. Определение скорости истечения жидкости где φ –коэффициент скорости 2. Определение расхода жидкости где µ –коэффициент расхода (зависит от формы насадка)

μ = 0. 82 μ = 0. 71 Коноидальный μ = 0. 94 Конический расходящийся Конический сходящийся Внутренний цилиндрический Внешний цилиндрический Виды насадков и их коэффициенты расхода μ = 0. 5 μ = 0. 98

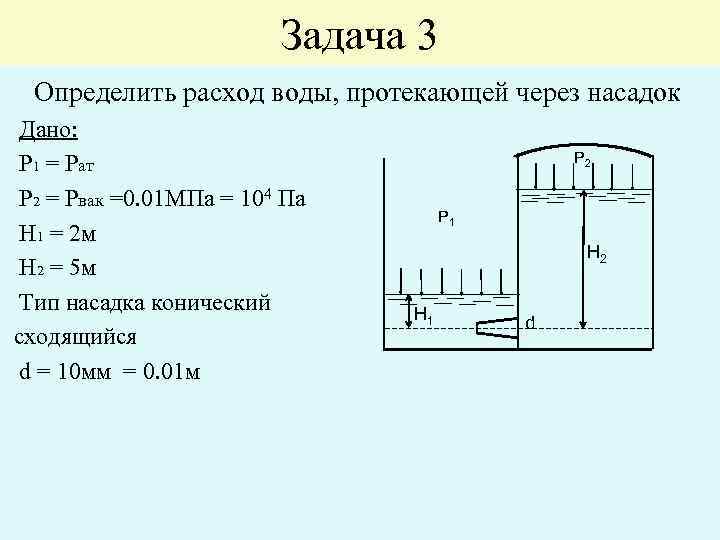Задача 3 Определить расход воды, протекающей через насадок Дано: Р 1 = Рат Р 2 = Рвак =0. 01 МПа = 104 Па Н 1 = 2 м Н 2 = 5 м Тип насадка конический сходящийся d = 10 мм = 0. 01 м Р 2 Р 1 Н 2 Н 1 d

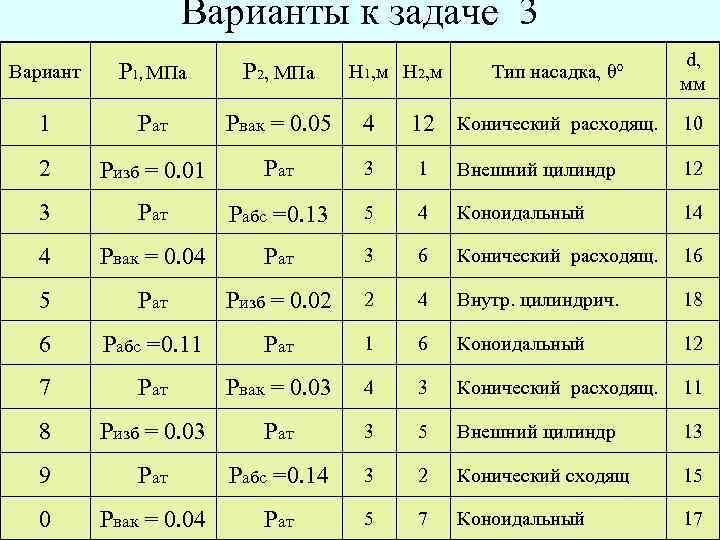Варианты к задаче 3 d, мм Вариант Р 1, МПа Р 2, МПа 1 Рат Рвак = 0. 05 4 2 Ризб = 0. 01 Рат 3 1 Внешний цилиндр 12 3 Рат Рабс =0. 13 5 4 Коноидальный 14 4 Рвак = 0. 04 Рат 3 6 Конический расходящ. 16 5 Рат Ризб = 0. 02 2 4 Внутр. цилиндрич. 18 6 Рабс =0. 11 Рат 1 6 Коноидальный 12 7 Рат Рвак = 0. 03 4 3 Конический расходящ. 11 8 Ризб = 0. 03 Рат 3 5 Внешний цилиндр 13 9 Рат Рабс =0. 14 3 2 Конический сходящ 15 0 Рвак = 0. 04 Рат 5 7 Коноидальный 17 Н 1, м Н 2, м Тип насадка, θ° 12 Конический расходящ. 10

Расход воды через насадок при постоянном напоре находят по формуле: [м 3/с] где - коэффициент расхода, принимается в зависимости от варианта насадка для конического сходящегося насадка = 0. 94. - площадь насадка, определяется по формуле: d - диаметр насадка; Hпр - приведенный напор, обеспечивающий истечение через насадок; Hпр определяется как результирующий напор слева и справа с учетом давления на свободную поверхность.

Р 1 = атмосферному давлению, что соответствует 105 Па; γ – удельный вес, γ = ρ ·g; ρ – плотность жидкости = 1000 кг/м 3 g – ускорение свободного падения. В этой задаче для более точного соответствия приведенной зависимости ускорение свободного падения g допускается принимать равным 10 м/с2. Рвак переводим в абсолютное давление. По определению вакуумметрическое давление – это давление, недостающее до атмосферного. Следовательно, абсолютное значение Рвак = 104 Па будет: 105 - 1· 104 = 0. 9 · 105 Па.

Знак " - " означает, что жидкость движется из правого резервуара в левый. Ответ: Q = 0. 00047 м 3/сек = 0. 47 л/сек.

Задача 4 Каким должен быть уклон лотка трапецеидального сечения, чтобы при глубине h пропустить заданный расход Q. Ширина лотка по низу b, коэффициент заложения откосов m, эквивалентная шероховатость стенок лотка n. Исходные данные принимать по варианту.

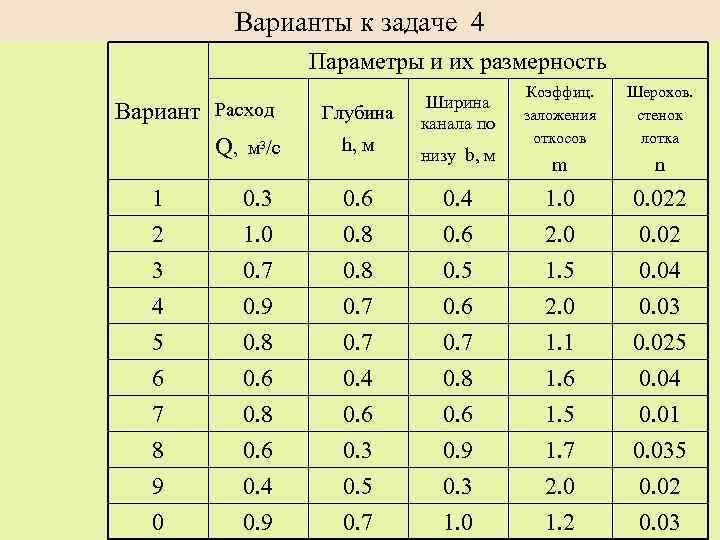Варианты к задаче 4 Параметры и их размерность Вариант Расход Q, м 3/с 1 2 3 4 5 6 7 8 9 0 0. 3 1. 0 0. 7 0. 9 0. 8 0. 6 0. 4 0. 9 Глубина h, м 0. 6 0. 8 0. 7 0. 4 0. 6 0. 3 0. 5 0. 7 Ширина канала по низу b, м 0. 4 0. 6 0. 5 0. 6 0. 7 0. 8 0. 6 0. 9 0. 3 1. 0 Коэффиц. заложения откосов Шерохов. стенок лотка m n 1. 0 2. 0 1. 5 2. 0 1. 1 1. 6 1. 5 1. 7 2. 0 1. 2 0. 02 0. 04 0. 03 0. 025 0. 04 0. 01 0. 035 0. 02 0. 03

Продольный уклон лотка i определяется из формулы Шези: где V - скорость движения жидкости; R - гидравлический радиус; C - коэффициент Шези. При заданном расходе Q и размере трапецеидального канала можно найти скорость: где - площадь живого сечения; для трапецеидального канала =(b+mh) × h м 2 ,

где b – ширина низа канала; m - коэффициент заложения откосов стенок канала; h - высота воды в канале. Гидравлический радиус: R = ω /χ где χ - смоченный периметр; для трапеции Коэффициент Шези C можно определить по формуле Маннинга где n – коэффициент шероховатости стенок русла.

Задача 4 а В каком режиме будет двигаться вода с температурой tº по каналу трапецеидального сечения при глубине h и ширина лотка по низу b, если заданный расход Q, а коэффициент заложения откосов m, Исходные данные принимать по варианту.

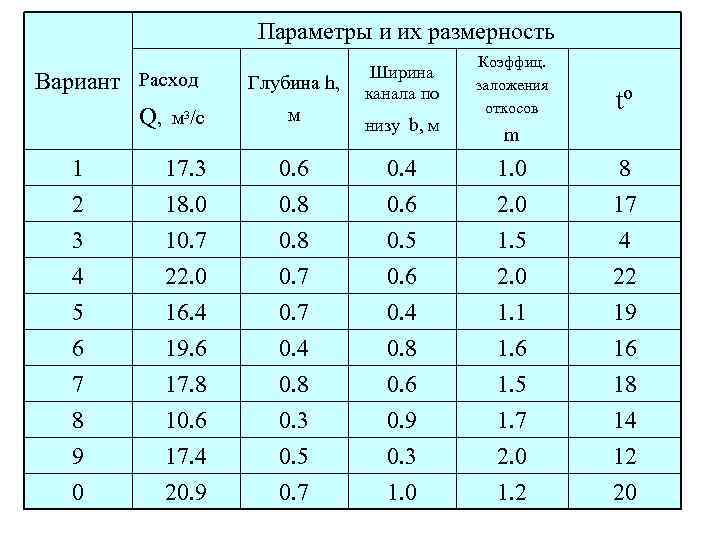Параметры и их размерность Вариант Расход Q, м 3/с 1 2 3 4 5 6 7 8 9 0 17. 3 18. 0 10. 7 22. 0 16. 4 19. 6 17. 8 10. 6 17. 4 20. 9 Глубина h, м 0. 6 0. 8 0. 7 0. 4 0. 8 0. 3 0. 5 0. 7 Ширина канала по низу b, м 0. 4 0. 6 0. 5 0. 6 0. 4 0. 8 0. 6 0. 9 0. 3 1. 0 Коэффиц. заложения откосов tº m 1. 0 2. 0 1. 5 2. 0 1. 1 1. 6 1. 5 1. 7 2. 0 1. 2 8 17 4 22 19 16 18 14 12 20

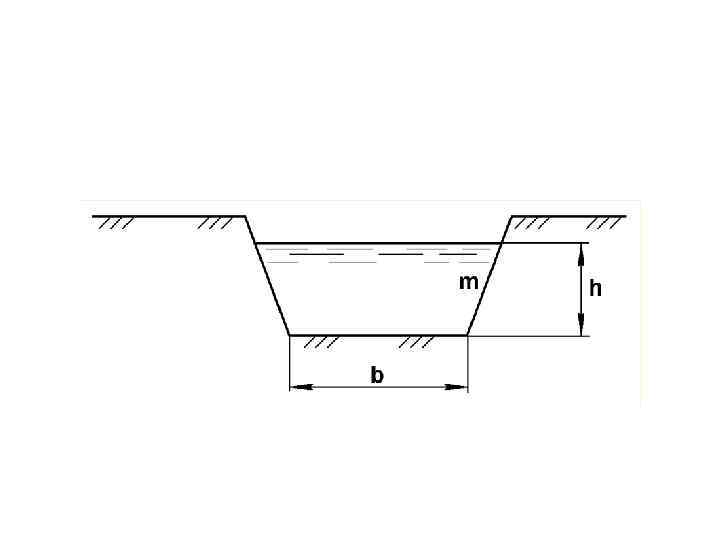
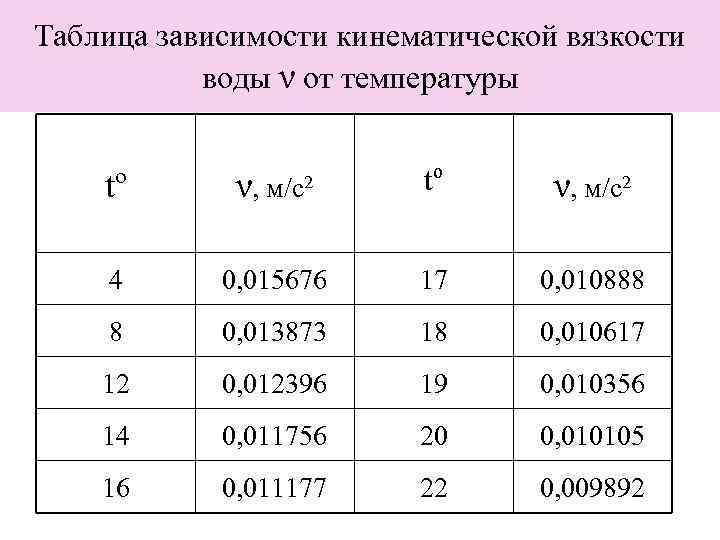Таблица зависимости кинематической вязкости воды ν от температуры tº ν, м/с2 4 0, 015676 17 0, 010888 8 0, 013873 18 0, 010617 12 0, 012396 19 0, 010356 14 0, 011756 20 0, 010105 16 0, 011177 22 0, 009892

Режимы движения жидкости в открытых руслах Движение жидкости может осуществляться в ламинарном либо в турбулентном режиме. Критерием режима движения служит число Рейнольдса Re. Для открытых русел при Re < 580 наблюдается ламинарный режим при Re > 580 турбулентный.

Как определить число Рейнольдса? Для открытых русел число Рейнольдса находят по формуле: Re = V· R / υ где V – скорость движения потока, м/с R – гидравлический радиус, м; R= ω/χ ω – площадь сечения потока, м ω = (b + m·h)·h χ – смоченный периметр, м χ = b + 2 h·√ 1+ m 2

Задача 5 Определить нормальную h 0, м и критическую h. К, м глубину, а также критический уклон i. К, если известны расход Q м 3/с, коэффициент шероховатости стенок канала n и ширина канала прямоугольного сечения b, м Дано: Q= 16 м 3/с , b= 8 м , n= 0, 025 , i= 0, 002

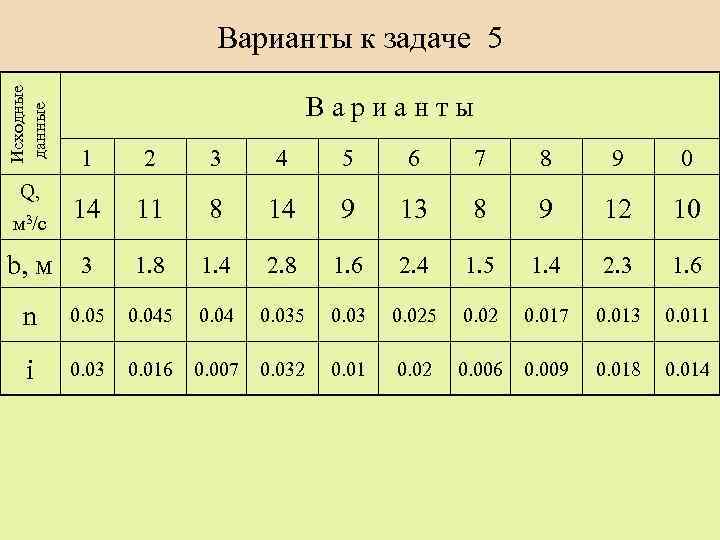Исходные данные Варианты к задаче 5 Варианты 1 2 3 4 5 6 7 8 9 0 14 11 8 14 9 13 8 9 12 10 b, м 3 1. 8 1. 4 2. 8 1. 6 2. 4 1. 5 1. 4 2. 3 1. 6 n 0. 05 0. 04 0. 035 0. 03 0. 025 0. 02 0. 017 0. 013 0. 011 i 0. 03 0. 016 0. 007 0. 032 0. 01 0. 02 0. 006 0. 009 0. 018 0. 014 Q, м 3/с

Нормальной называется глубина h 0, м, которая устанавливается при заданном расходе Q м 3/с в условиях равномерного движения. Найти ее можно из уравнения равномерного движения: Если собрать все величины уравнения, зависящие от глубины потока h в расходной характеристике (К): то уравнение примет вид: Эта расходная характеристика будет соответствовать нормальной глубине h 0, которая находится методом подбора или по графику.

Подбор заключается в том, чтобы задаваясь разными глубинами h получить расходную характеристику, вычисленную для равномерного движения. Удобнее это выполнять в виде таблицы. Коэффициент Шези С определяют по формуле: Подставляя данные величины вычисляем К

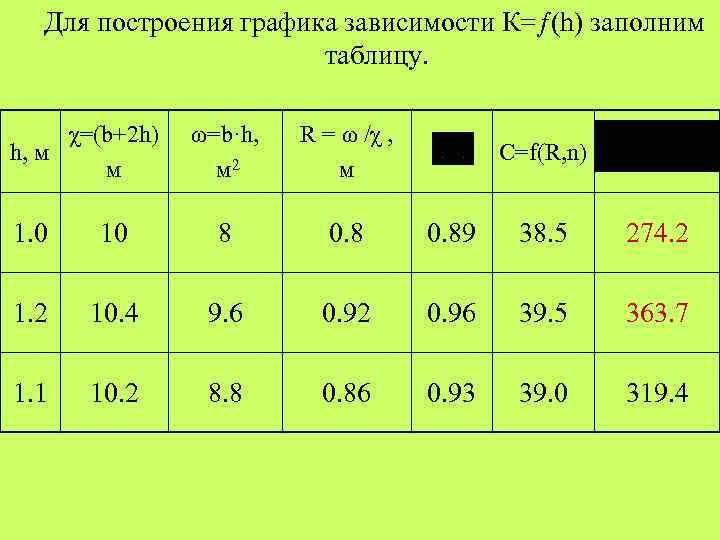Для построения графика зависимости К=ƒ(h) заполним таблицу. χ=(b+2 h) h, м м ω=b·h, м 2 R = ω /χ , м C=f(R, n) 1. 0 10 8 0. 89 38. 5 274. 2 10. 4 9. 6 0. 92 0. 96 39. 5 363. 7 1. 1 10. 2 8. 8 0. 86 0. 93 39. 0 319. 4

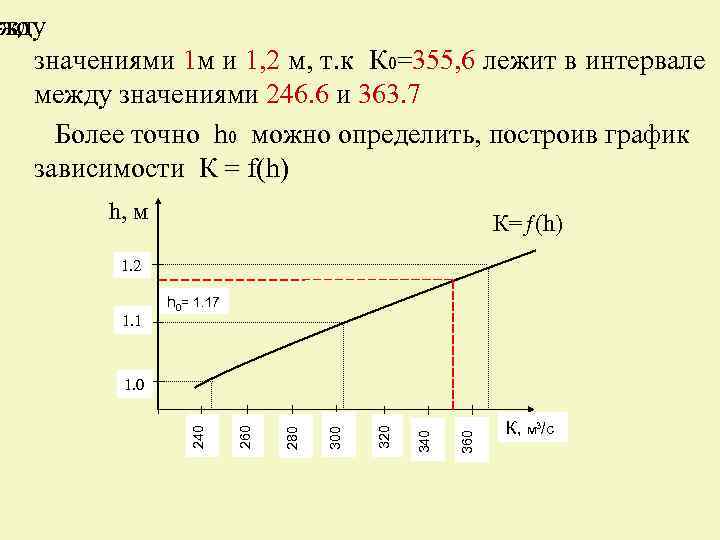ть -то жду значениями 1 м и 1, 2 м, т. к К 0=355, 6 лежит в интервале между значениями 246. 6 и 363. 7 Более точно h 0 можно определить, построив график зависимости К = f(h) h, м К=ƒ(h) 1. 2 1. 1 h 0= 1. 17 360 340 320 300 280 260 240 1. 0 К, м 3/с

Критическая глубина hk, устанавливается при критическом состоянии потока, когда он обладает минимальной энергией. hk можно найти из уравнения критического состояния потока: где a – коэффициент кинетической энергии равный 1. 1; g – ускорение свободного падения 9, 81 м/с2; k – площадь сечения потока при его критическом состоянии, т. е когда h = hk; b – ширина потока по свободной поверхности.

В нашем случае прямоугольного сечения канала hk можно выразить: Критический уклон ik – это уклон, при котором равномерное движении происходит с критической глубиной. Его можно найти по формуле: где k , Ck , Rk найдем при hk

h, м 0. 76 K=ω·C·√R, C=f(R, n) м 3/с χ=(b+2 h), ω=b·h, R = ω /χ , м м 2 м 9. 52 6. 08 0. 64 0. 8 37. 1 180. 45

Задача 6 Определить глубину потока в сжатом сечении за перепадом P и сопряженную с ней глубину. Значения расхода Q м 3/с; ширины потока b, м критической глубины hk, м взять из предыдущей задачи. Коэффициент скорости принять равным 0, 9. Высота перепада Р=1, 4 м.

Величины и зависят от запаса энергии, которой обладает поток и высоты перепада P, м. Энергию находят по формуле: где a - коэффициент кинетической энергии, равен 1; hk - принимаем по предыдущей задаче, равная 0, 76 м; Q - расход потока из предыдущей задачи, принимаем равным ; b – ширина потока принимается по ширине канала из предыдущей задачи равным 8 м.

Находим величину По этой величине и по коэффициенту скорости =0, 9 находим по графику значения коэффициентов c=0, 46 и С помощью этих коэффициентов по зависимостям: и находим: и

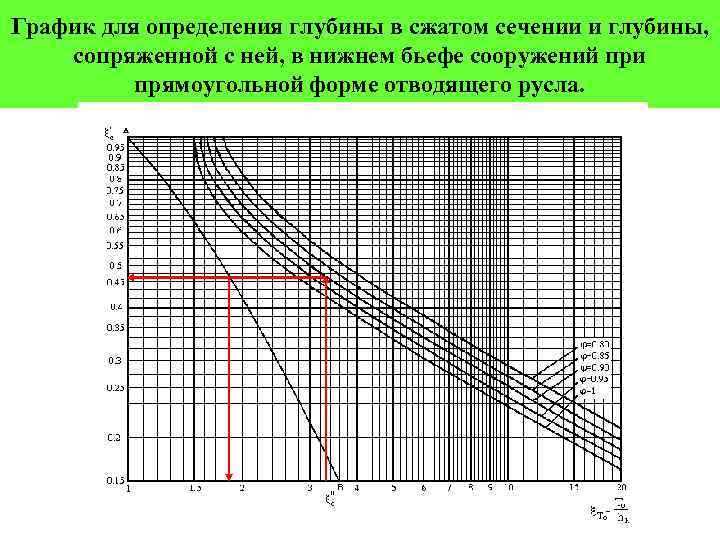График для определения глубины в сжатом сечении и глубины, сопряженной с ней, в нижнем бьефе сооружений при прямоугольной форме отводящего русла.

Задача 7 Рассчитать малый мост при расходе =13 м 3/с Принять нормальную h 0 и критическую глубину hk по результатам, полученным в 5 задаче. По значению нормальной глубины h 0 принимаем бытовую глубину hб. Определяем условия протекания потока под мостом Если - hкр > hб, то протекание свободное (незатопленное). Если - hкр < hб, то протекание несвободное (затопленное). Протекание несвободное (h 0 = 1. 17 м. , hк = 0. 76 м. т. е. hкр < hб)

Дано: Q = 13 м 3/с; h 0 = 1. 17 м При расчёте малого моста определяют: 1. Отверстие моста 2. Напор перед мостом Отверстие моста b по формуле: где hб - глубина потока под мостом. В условиях несвободного протекания hб принимают равным hо (1. 17 м). Vм - скорость потока под мостом находят из уравнения:

Согласно действующим нормам и стандартам расстояния в свету между опорами моста (отверстиями) принимаются: 2, 3, 4, 5, 6, 7. 5, 10 м В соответствии с этими нормами принимаем отверстие равное 4 метрам. Напор перед мостом Hм находим из формулы:

φ- где коэффициент скорости, который находят по формуле: - коэффициент сжатия, принимают в зависимости от характера входного отверстия по таблице. (Примем ε = 0. 8) Напор перед мостом :

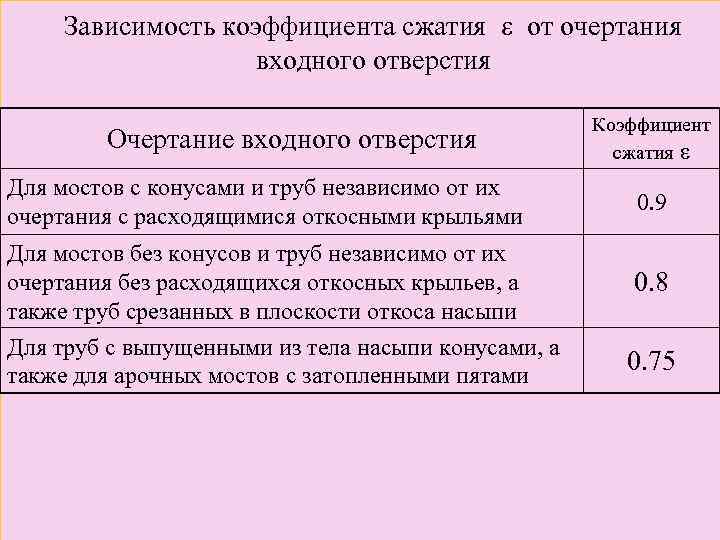Зависимость коэффициента сжатия от очертания входного отверстия Очертание входного отверстия Коэффициент сжатия ε Для мостов с конусами и труб независимо от их очертания с расходящимися откосными крыльями 0. 9 Для мостов без конусов и труб независимо от их очертания без расходящихся откосных крыльев, а также труб срезанных в плоскости откоса насыпи 0. 8 Для труб с выпущенными из тела насыпи конусами, а также для арочных мостов с затопленными пятами 0. 75

Протекание незатопленное (hкр > h 0. ) Дано: Q = 13 м 3/с; hкр = 1, 9 м; h 0 = 1, 17 м К hб Находим отверстие моста по формуле: где hм - глубина под мостом, принимаемая по значению hк=1, 3 м

Скорость под мостом определяем по формуле: Найдём отверстие под мостом Согласно действующим нормам и стандартам расстояния в свету между опорами моста (отверстиями) принимаются: 2, 3, 4, 5, 6, 7. 5, 10 м В соответствии с этими нормами принимаем ближайшее стандартное отверстие равное 3 метрам. Напор перед мостом Hм находим из формулы:

μ – коэффициент расхода, зависит от типа устоев моста. Тип устоев моста μ Облегчённый тип Славинского 1. 42 С откосыми крыльями 1. 55 С обратными стенками 1. 6