Гидравлика Наука о законах равновесия и движения жидкостей

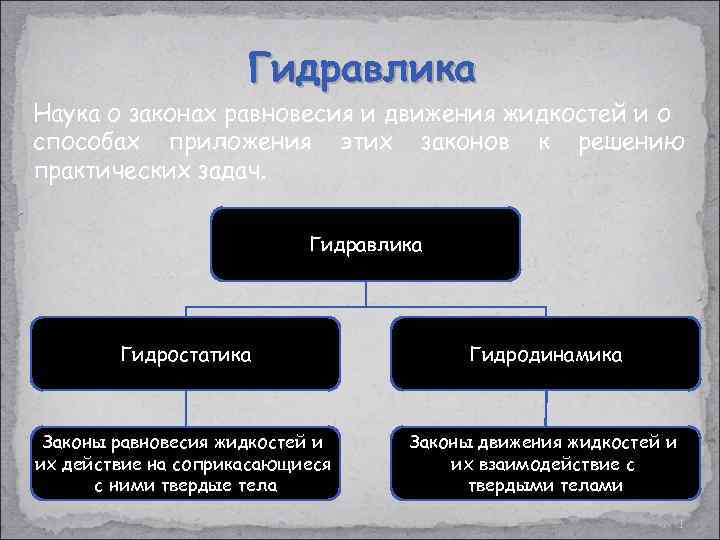Гидравлика Наука о законах равновесия и движения жидкостей и о способах приложения этих законов к решению практических задач. Гидравлика Гидростатика Гидродинамика Законы равновесия жидкостей и их действие на соприкасающиеся с ними твердые тела Законы движения жидкостей и их взаимодействие с твердыми телами 1

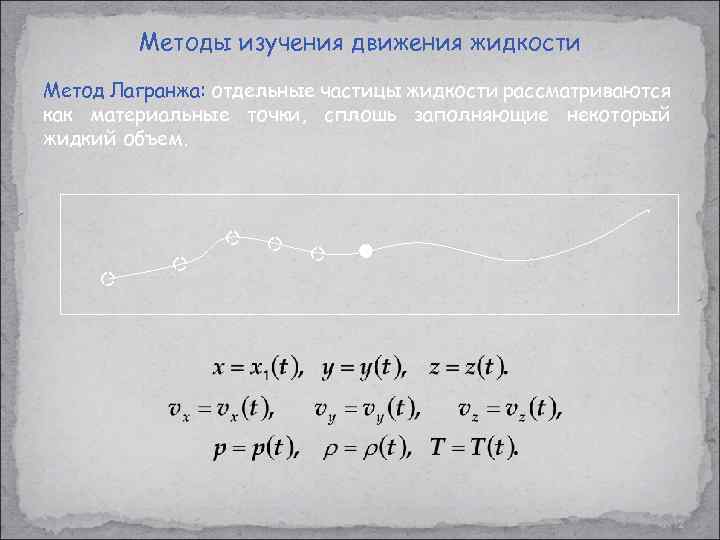Методы изучения движения жидкости Метод Лагранжа: отдельные частицы жидкости рассматриваются как материальные точки, сплошь заполняющие некоторый жидкий объем. 2

Методы изучения движения жидкости Метод Эйлера: наблюдается изменение параметров движения частиц жидкости, проходящих через данную фиксированную точку пространства, с течением времени. 3

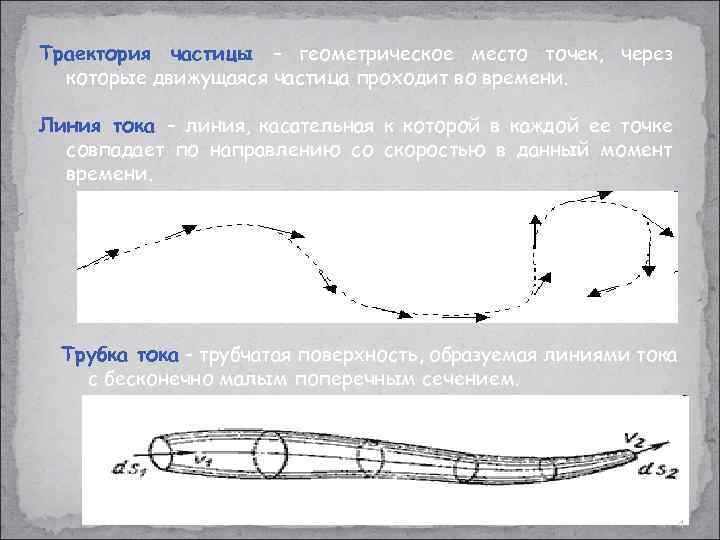Траектория частицы – геометрическое место точек, через которые движущаяся частица проходит во времени. Линия тока – линия, касательная к которой в каждой ее точке совпадает по направлению со скоростью в данный момент времени. Трубка тока - трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. 4

Стационарное (установившееся) течение – в каждой фиксированной точке пространства все гидродинамические величины не зависят от времени. (21) Нестационарное (неустановившееся) течение – параметры меняются по времени. (22) 5

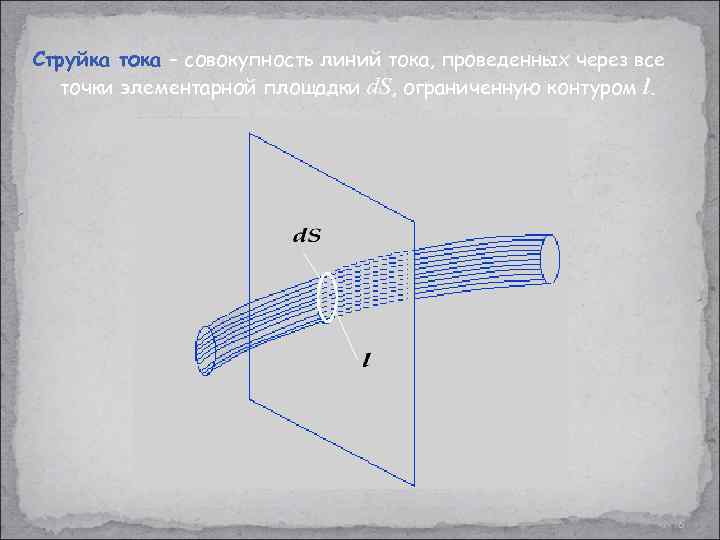Струйка тока – совокупность линий тока, проведенных через все точки элементарной площадки d. S, ограниченную контуром l. 6

Объемный расход – объем жидкости, протекающий в единицу времени через данную поверхность. Элементарный расход Полный расход (23) Живое сечение - площадь поперечного сечения потока, перпендикулярное к направлению течения. 7

Смоченный периметр - часть периметра живого сечения, ограниченное твердыми стенками. Гидравлический радиус - отношение живого сечения потока к смоченному периметру. (24) 8

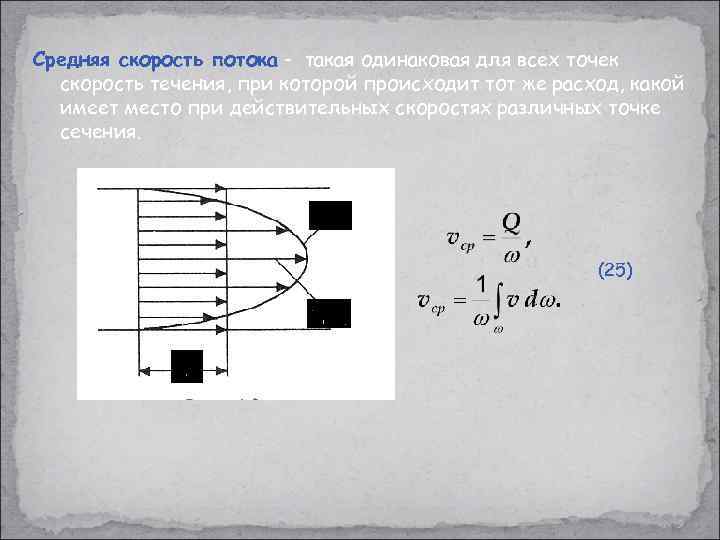Средняя скорость потока - такая одинаковая для всех точек скорость течения, при которой происходит тот же расход, какой имеет место при действительных скоростях различных точке сечения. (25) 9

Закон сохранения массы (уравнение неразрывности) Расход массы – количество жидкости, которое протекает через поперечное сечение (S) за единицу времени. Объемный расход, Массовый расход, (26) (27) 10

Закон сохранения массы (уравнение неразрывности) (28) (29) (30) (29’) 11

Закон сохранения массы (31) (32) Полная производная – производная, вычисленная вдоль траектории движения частицы, показывает изменение параметра движущейся частицы жидкости. 12

Закон сохранения массы (частные случаи) (29) Установившееся течение: Течение несжимаемой жидкости (ρ=const): Одномерное течение в канале переменного сечения (29’) 13

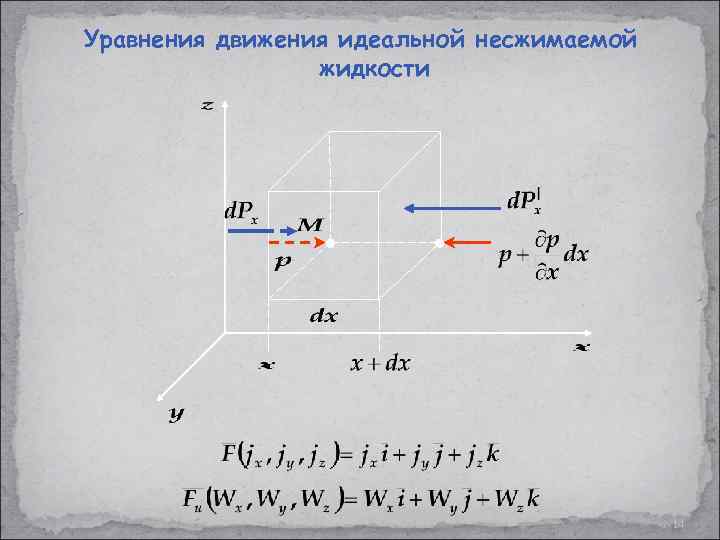Уравнения движения идеальной несжимаемой жидкости 14

Уравнения движения идеальной несжимаемой жидкости Система дифференциальных уравнений Эйлера (33) 15

Уравнения движения вязкой несжимаемой жидкости Система дифф. уравнений Навье-Стокса (34) - кинематический коэффициент вязкости, [м 2/с] - динамический коэффициент вязкости, [Па с] Закон Ньютона (35) (36) 16

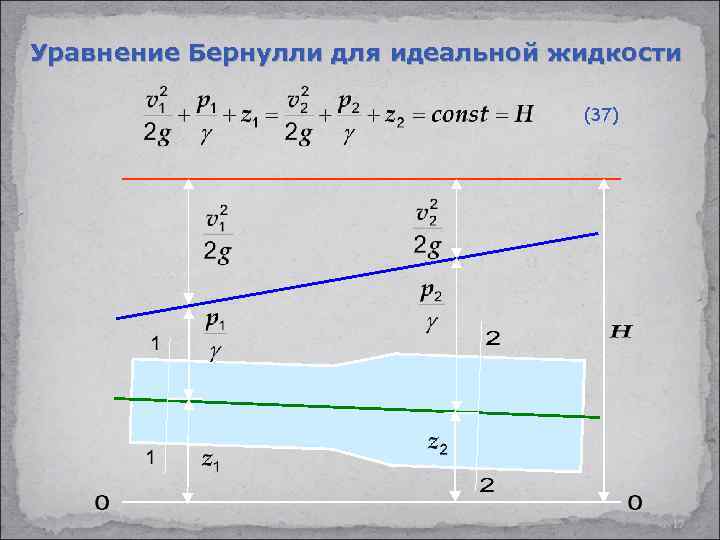Уравнение Бернулли для идеальной жидкости (37) 17

Уравнение Бернулли для идеальной жидкости - удельная потенциальная энергия положения частицы жидкости (энергия, отнесенная к единице веса) - удельная потенциальная энергия давления частицы жидкости (энергия, отнесенная к единице веса) - удельная кинетическая энергия частицы жидкости (энергия, отнесенная к единице веса) 18

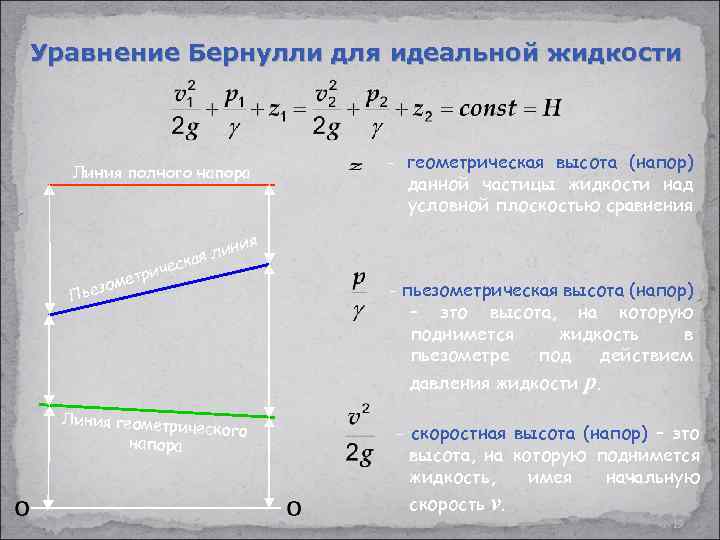Уравнение Бернулли для идеальной жидкости Линия полного напора - геометрическая высота (напор) данной частицы жидкости над условной плоскостью сравнения ия лин кая чес три оме ьез П - пьезометрическая высота (напор) – это высота, на которую поднимется жидкость в пьезометре под действием давления жидкости p. Линия геометр ического напора - скоростная высота (напор) – это высота, на которую поднимется жидкость, имея начальную скорость v. 19

Уравнение Бернулли для реальной жидкости (38) Гидравлический уклон – характеризует относительное изменение полного напора на единицу длины (39) Пьезометрический уклон 20

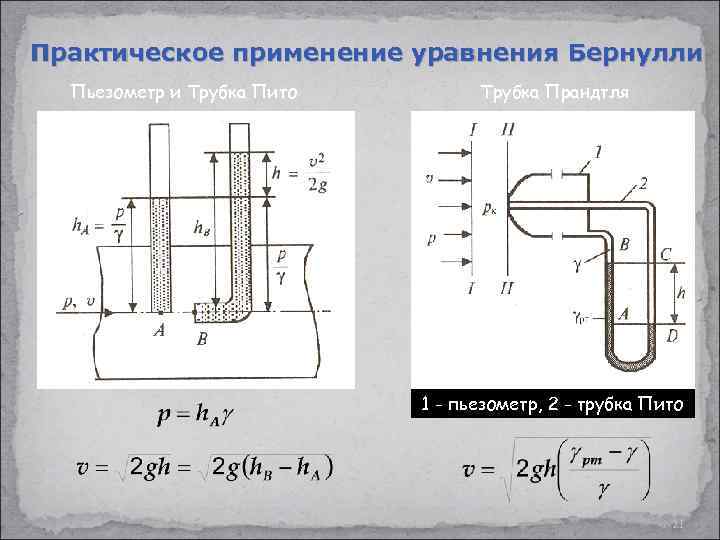Практическое применение уравнения Бернулли Пьезометр и Трубка Пито Трубка Прандтля 1 - пьезометр, 2 - трубка Пито 21

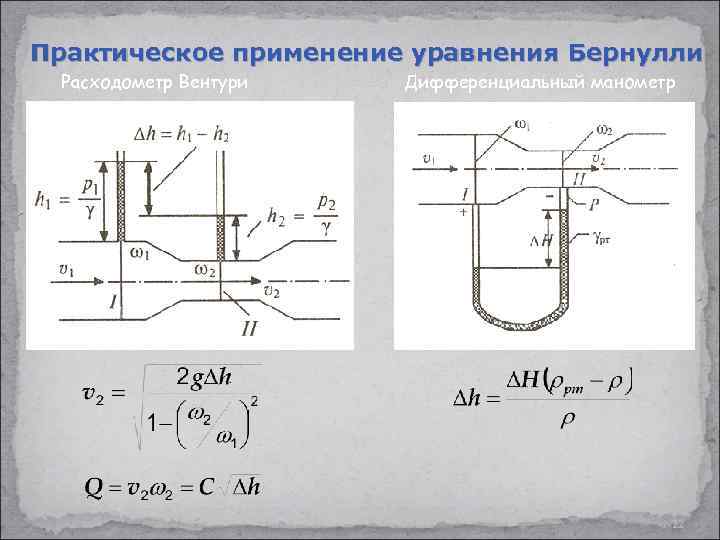Практическое применение уравнения Бернулли Расходометр Вентури Дифференциальный манометр 22

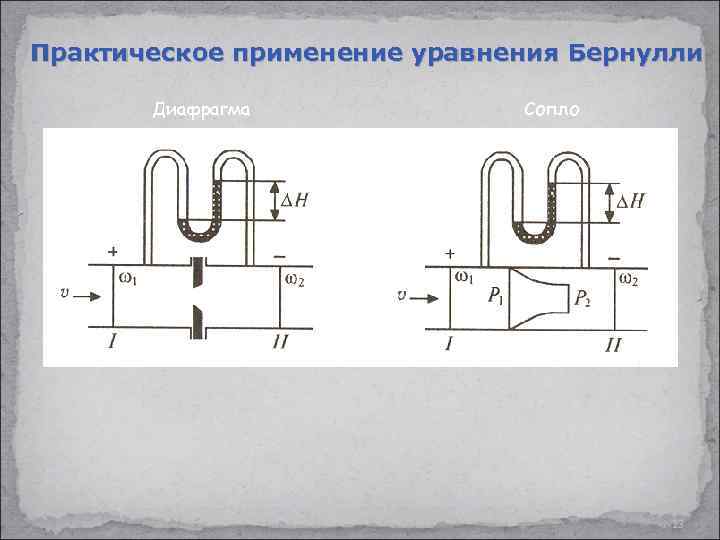Практическое применение уравнения Бернулли Диафрагма Сопло 23

Задачи 5. Определить расход Q воды в трубопроводе диаметром D, плавно сужающимся до диаметра d, если показания пьезометров до сужения h 1 и после сужения h 2. Рассмотреть течение идеальной жидкости. Решение: Запишем уравнение (37) для данного трубопровода. Из уравнения неразрывности (29’) найдем скорость потока в узкой трубе И подставим в уравнение Бернулли 24

Задачи 6. Решить задачу обратную задаче 5. Дан расход жидкости Q, диаметры труб D и d, задано давление в трубопроводе большего диаметра p 1. Определить давление в трубе меньшего диаметра (жидкость – вода). 25

Основы теории гидродинамического подобия (32) (35) Геометрическое подобие Динамическое подобие Кинематическое подобие – это подобие тех поверхностей, которые ограничивают потоки. – все силы, вызывающие движение в образце должны изменяться в соответствии с изменениями аналогичных сил в модели. – это подобие скоростей, ускорений и перемещений потоков. 26

Основы теории гидродинамического подобия Образец Модель - константа геометрического подобия 27

Основы теории гидродинамического подобия Образец Модель - константа динамического подобия 28

Основы критерии подобия - число Рейнольдса: характеризует отношение сил инерции к силам вязкости - число Эйлера: характеризует отношение сил давления к силам инерции - число Фруда: характеризует отношение сил тяжести к силам инерции - число Прандтля: характеризует отношение теплового потока, обусловленного работой сил трения, к конвективному тепловому потоку - число Струхаля: процесса характеризует нестационарность 29

- число Грасгофа: характеризует подъемную силу, возникающую в жидкости вследствие разности плотности из-за изменения температуры - диффузионное число Архимеда: характеризует подъемную силу, которая обусловлена составом жидкости (примеси …) - число Вебера: характеризует отношение сил инерции к силам поверхностного натяжения - число Пекле: характеризует отношение конвективного тепла (потока тепла, переносимого жидкостью) к потоку тепла, обусловленного теплопроводностью - число Фурье: характеризует быстроту влияния изменения тепловых условий в окружающей среде на изменение температуры внутри среды 30

Задачи 7. Определить скорость потока в трубе диаметром 3 см, при которой число Рейнольдса будет равно 3230. Рассмотреть 3 вида сред: вода, глицерин и воздух. Решение: вода глицерин воздух 8. Определить число Рейнольса в трубе диаметром 300 мм, если протекающий в ней расход составляет 0. 136 м 3/с. (вода) 31

Гидравлические сопротивления Потери энергии (уменьшение гидравлического напора) возникают в движущейся жидкости как на сравнительно длинных участках, так и на коротких. Линейные потери - потери напора распределяются (иногда равномерно) по длине трубопровода. Местные потери – потери напора сосредоточены на очень коротких участках, длиной которых можно пренебречь (вентили, всевозможные закругления, сужения, расширения и т. д). Источником потерь во всех случаях является вязкость жидкости. (40) (41) 32

Линейные потери – это потери напора на трение на прямых участках трубопроводов. Формула Вейсбаха-Дарси (42) - коэффициент гидравлического сопротивления (коэффициент трения) – безразмерная величина - внутренний диаметр и длина участка трубопровода - средняя скорость потока в трубопроводе 33

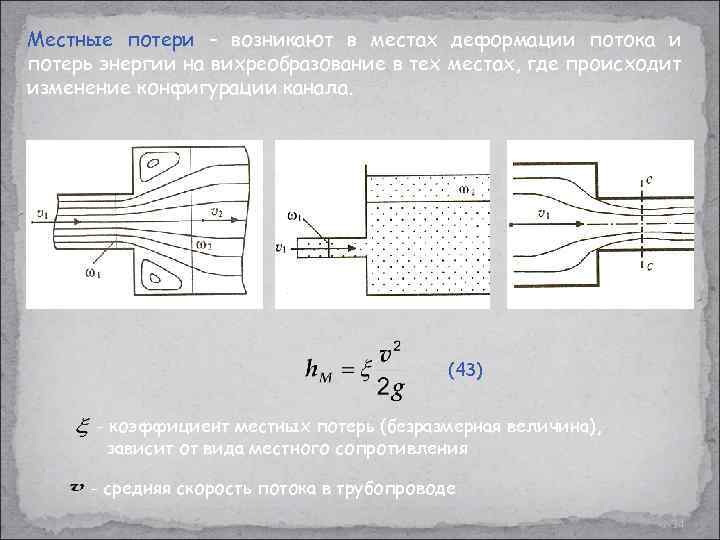Местные потери – возникают в местах деформации потока и потерь энергии на вихреобразование в тех местах, где происходит изменение конфигурации канала. (43) - коэффициент местных потерь (безразмерная величина), зависит от вида местного сопротивления - средняя скорость потока в трубопроводе 34

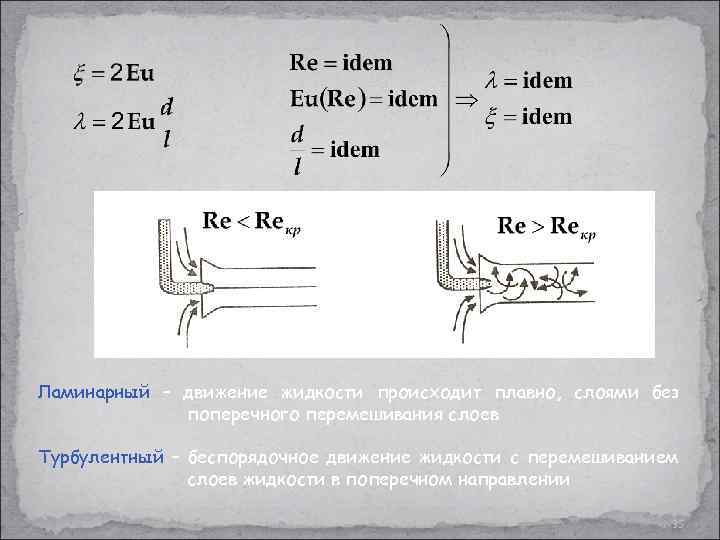Ламинарный – движение жидкости происходит плавно, слоями без поперечного перемешивания слоев Турбулентный – беспорядочное движение жидкости с перемешиванием слоев жидкости в поперечном направлении 35

Равномерное движение жидкости I – участок стабилизации ламинарного течения II – участок стабилизированного (равномерного) течения 36

Вдоль равномерного потока уменьшается только потенциальная энергия, которая расходуется на потери напора. 37

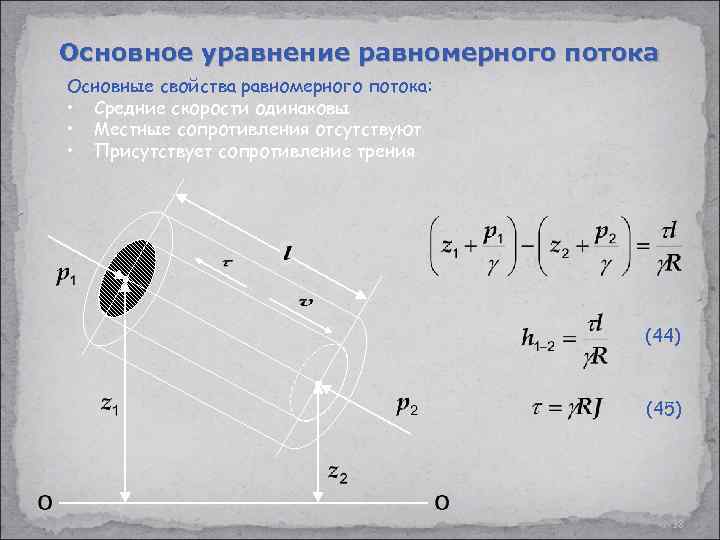Основное уравнение равномерного потока Основные свойства равномерного потока: • Средние скорости одинаковы • Местные сопротивления отсутствуют • Присутствует сопротивление трения (44) (45) 38

Ламинарное движение жидкости Закон Ньютона (46) (47) (48) (49) 39

Ламинарное движение жидкости (50) (51) Формулы Гагена-Пуазейля (52) 40

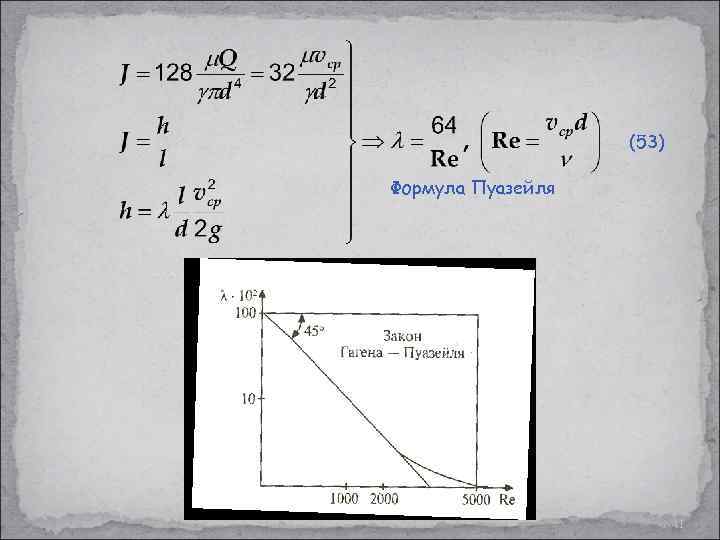(53) Формула Пуазейля 41

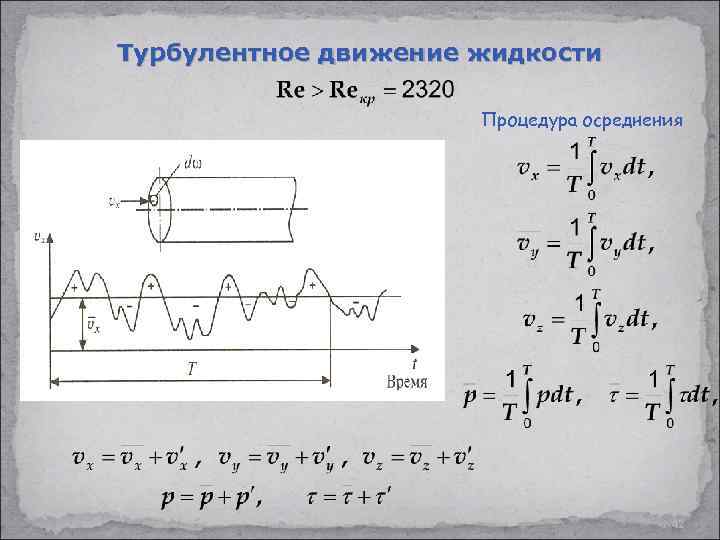Турбулентное движение жидкости Процедура осреднения 42

Структура турбулентного потока Динамическая скорость (54) 43

Турбулентное движение жидкости (55) (56) 44

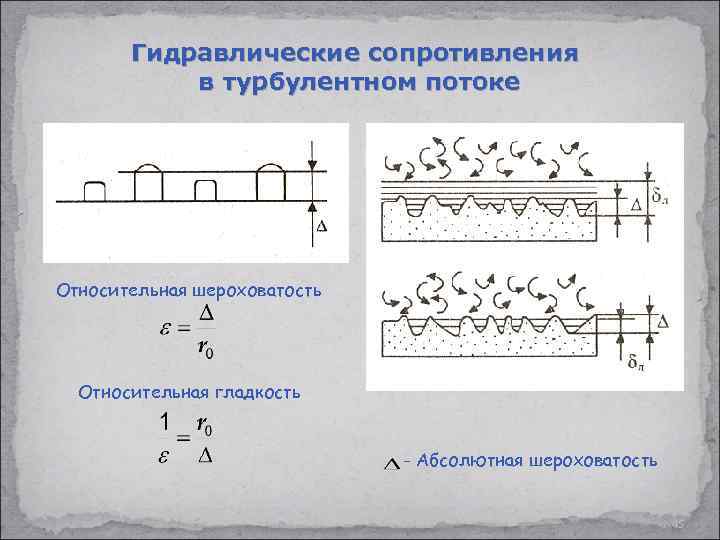Гидравлические сопротивления в турбулентном потоке Относительная шероховатость Относительная гладкость - Абсолютная шероховатость 45

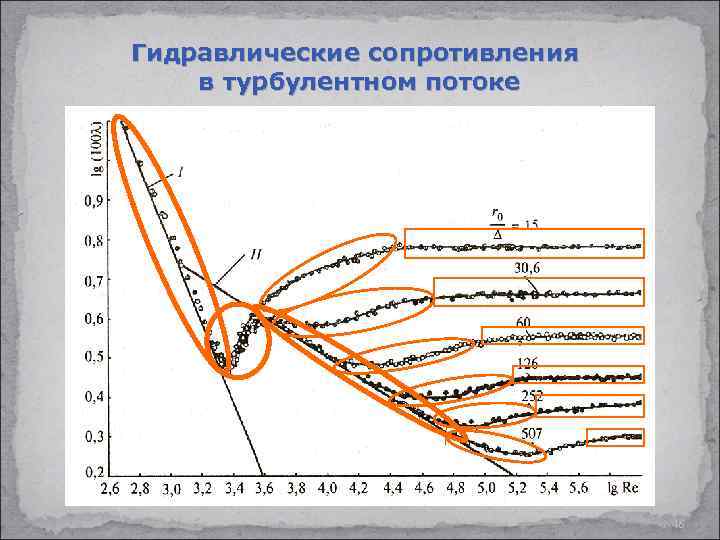Гидравлические сопротивления в турбулентном потоке 46

Зона ламинарного режима Переходная зона Зона гидравлически гладких труб Зона шероховатых труб Зона вполне шероховатых труб 47

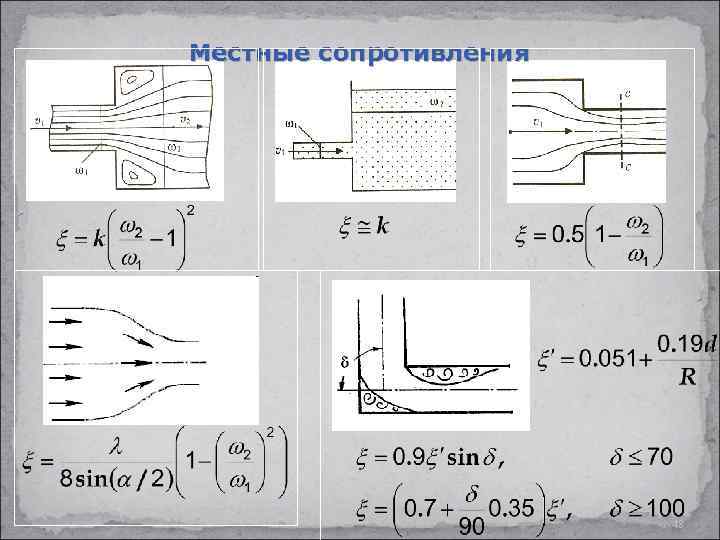Местные сопротивления 48

Задачи 9. По трубопроводу диаметром d и длиной l движется жидкость (коэффициент вязкости 10 -6 м 2/с). Определить потурю напора h, при которой происходит смена ламинарного режима течения на турбулентный. Исходные данные: Решение: Потери напора определим по формуле Вейсбаха-Дарси (42) Коэффициент линейных потерь найдем по формуле Пуазейля (53) Скорость найдем из числа Рейнольдса тогда 10. Решить задачу 9 при условии, что жидкость в трубопроводе – керосин 49

Коэффициент сопротивления системы (57) (57’) 50

Формулы для определения потерь напора Формула Шези Формула Павловского Вторая водопроводная формула 51

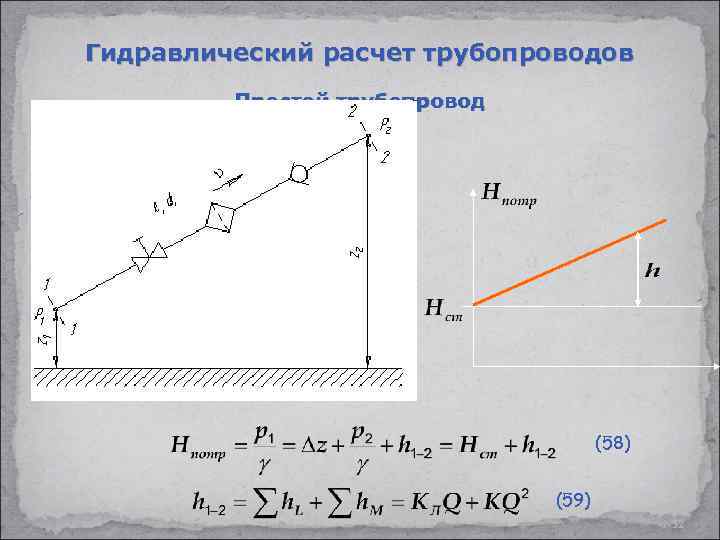Гидравлический расчет трубопроводов Простой трубопровод (58) (59) 52

Сложный трубопровод 53

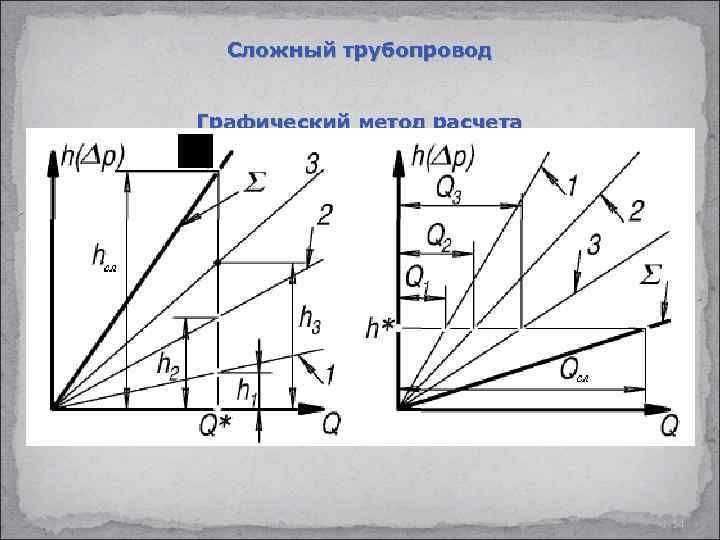Сложный трубопровод Графический метод расчета 54

Задачи 11. Найти потери в двух последовательно соединенных трубопроводов, работающих в зоне вполне шероховатых труб при следующих исходных данных: Решение: В зоне вполне шероховатых труб Найдем скорость Определим потери по формуле (57) 12. Решить задачу 11 графическим методом. 55

Гидравлический удар в трубах Резкое изменение давления в трубопроводе вследствие резкого изменения в нем скорости движения. Резкое закрытие крана приводит к остановке жидкости и росту давления в трубе (стенки трубы расширяются). Область повышенного давления распространяется на всю трубу. Затем жидкость начинает вытекать обратно в резервуар (стенки трубы возвращаются в первоначальное состояние) Жидкость приобретает ту же скорость, направленную в обратную сторону. Жидкость пытается оторваться от крана, создавая отрицательную ударную волну от крана к резервуару (стенки трубы сжимаются). Область пониженного давления распространяется на всю трубу. Под действием перепада давления жидкость снова начинает втекать в трубу. Процесс повторяется. 56

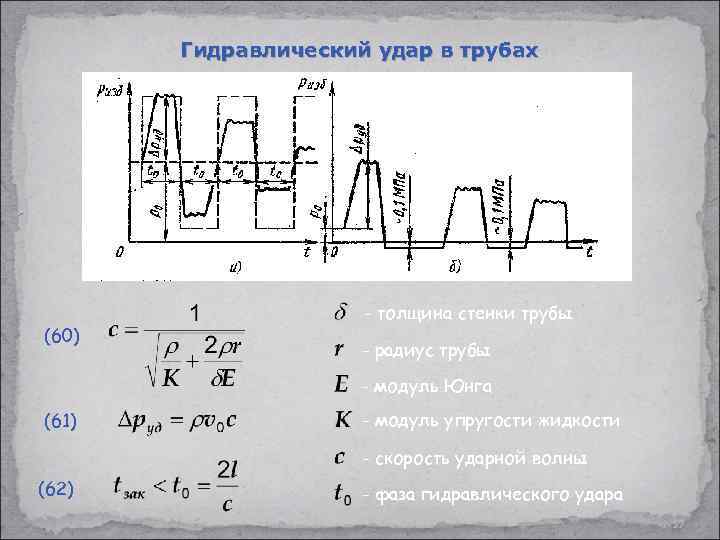Гидравлический удар в трубах (60) - толщина стенки трубы - радиус трубы - модуль Юнга (61) - модуль упругости жидкости - скорость ударной волны (62) - фаза гидравлического удара 57

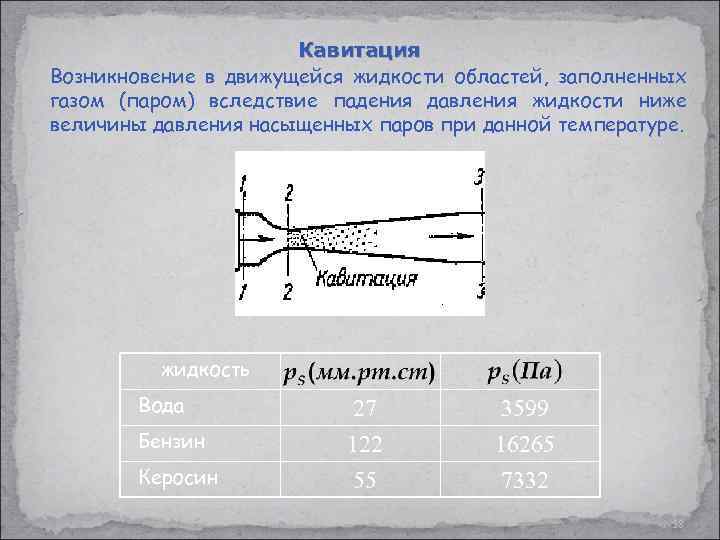Кавитация Возникновение в движущейся жидкости областей, заполненных газом (паром) вследствие падения давления жидкости ниже величины давления насыщенных паров при данной температуре. жидкость Вода Бензин Керосин 27 122 55 3599 16265 7332 58

Неньютоновские жидкости Закон Ньютона Ньютоновские жидкости (35) (63) Неньютоновские жидкости 4 1 2 3 59

Неньютоновские жидкости (основные понятия) Неньютоновские (аномальные) жидкости – это жидкости, которые не подчиняются основному закону внутреннего трения Ньютона. Кривые течения (реологические кривые) – это кривые, изображающие графически зависимость между градиентом скорости течения и возникающим в ней касательным напряжением. Различают: 1 – Дилатантная неньютоновская жидкость (при течении загустевают: мокрый песок, крахмальное молочко, карамель); 2 – Обычная ньютоновская жидкость (вода, масла, ацетон, водные растворы); 3 – Псевдопластичная неньютоновская жидкость (при течении разжижаются: лава, кетчуп, кровь, краски и лак для ногтей); 4 – Вязко-пластичная неньютоновская жидкость (буровые растворы, сточные грязи, масляные краски, зубная паста, глинистые и цементные растворы, парафинистые нефти). 60

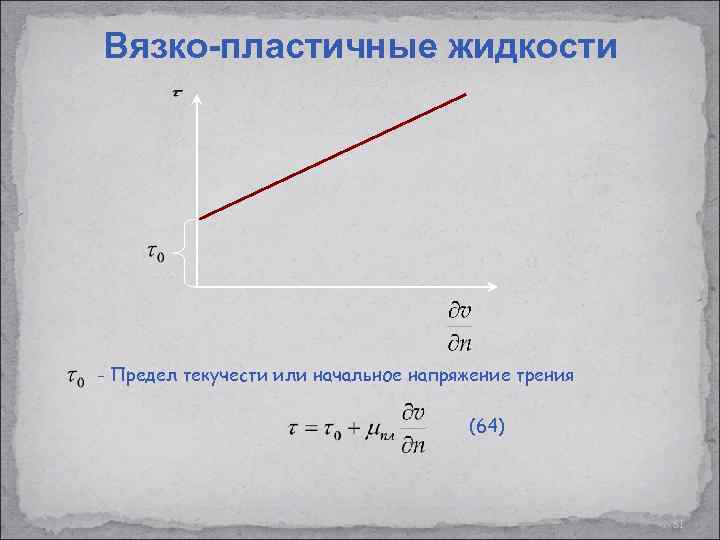Вязко-пластичные жидкости - Предел текучести или начальное напряжение трения (64) 61

Статика вязко-пластичных жидкостей Сообщающиеся сосуды (65) 62

Статика вязко-пластичных жидкостей Наклонная плоскость (66) 63

Движение вязко-пластичных жидкостей по трубам 1 2 Условие начала движения вязко-пластичной жидкости в трубопроводе: (67) 64

Движение вязко-пластичных жидкостей по трубам Центральное ядро (68) (69) формула Букингема Обобщенный критерий Рейнольдса 65

Задачи 13. В горизонтальном трубопроводе длиной l, диаметром d находится нефть, характеризующаяся свойствами вязко-пластичной жидкости. Её начальное напряжение сдвига, плотность и вязкость известны. Насос может создать разность давлений по концам трубопровода ∆р. Необходимо определить будет ли при этом нефть перемещаться в трубопроводе. Решение: Определим будет ли выполняться условие начала движения вязко-пластичной жидкости в трубопроводе (67): Действующая разность напоров 48, 01 м превышает разность напоров, соответствующую началу движения жидкости 24, 01. Поэтому нефть в трубопроводе будет двигаться. 14. Для задачи 13 определить расход с которым будет перемещаться нефть по трубопроводу и обобщенный критерий Рейнольдса. 66