Гетероскедастичность и автокоррелированность случайного члена патология МНК

Гетероскедастичность и автокоррелированность случайного члена (патология МНК)

Гетероскедастичность и ее последствия • Гомоскедастичность – дисперсия Var(ui) одинакова для всех наблюдений (т. е. одинаковый разброс). • Важность гомоскедастичности: – коэффициенты регрессии имеют наименьшую дисперсию среди несмещенных оценок – при нарушении гомоскедастичности оценки стандартных ошибок коэффициентов регрессии неверны

Обнаружение гетероскедастичности • Тест ранговой корреляции Спирмена – абсолютные величины остатков и значения x коррелированы – Коэффициент ранговой корреляции где Di – разность между рангом x и рангом остатка e Теорема Если коэффициент корреляции для генеральной совокупности равен нулю, то тестовая статистика имеет нормальное распределение N(0, 1). Замечание В множественной регрессии проверка гипотезы выполняется с использованием любой переменной.

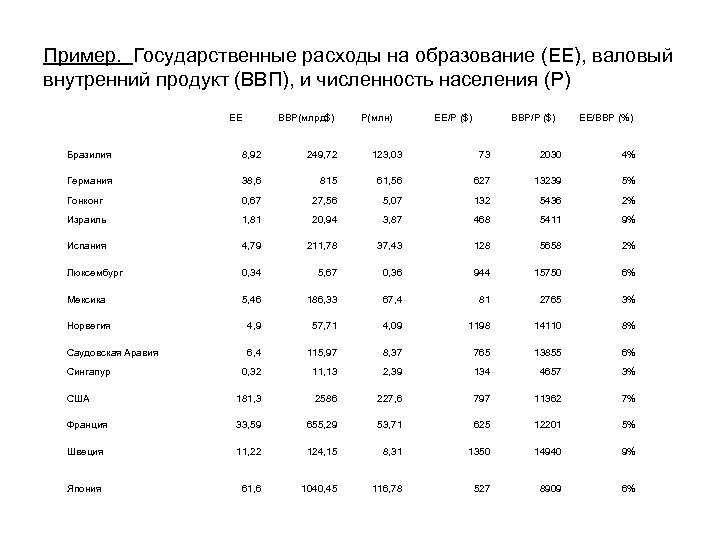Пример. Государственные расходы на образование (EE), валовый внутренний продукт (ВВП), и численность населения (P) EE BBP(млрд$) P(млн) EE/P ($) BBP/P ($) EE/BBP (%) Бразилия 8, 92 249, 72 123, 03 73 2030 4% Германия 38, 6 815 61, 56 627 13239 5% Гонконг 0, 67 27, 56 5, 07 132 5436 2% Израиль 1, 81 20, 94 3, 87 468 5411 9% Испания 4, 79 211, 78 37, 43 128 5658 2% Люксембург 0, 34 5, 67 0, 36 944 15750 6% Мексика 5, 46 186, 33 67, 4 81 2765 3% Норвегия 4, 9 57, 71 4, 09 1198 14110 8% Саудовская Аравия 6, 4 115, 97 8, 37 765 13855 6% 0, 32 11, 13 2, 39 134 4657 3% США 181, 3 2586 227, 6 797 11362 7% Франция 33, 59 655, 29 53, 71 625 12201 5% Швеция 11, 22 124, 15 8, 31 1350 14940 9% Япония 61, 6 1040, 45 116, 78 527 8909 6% Сингапур

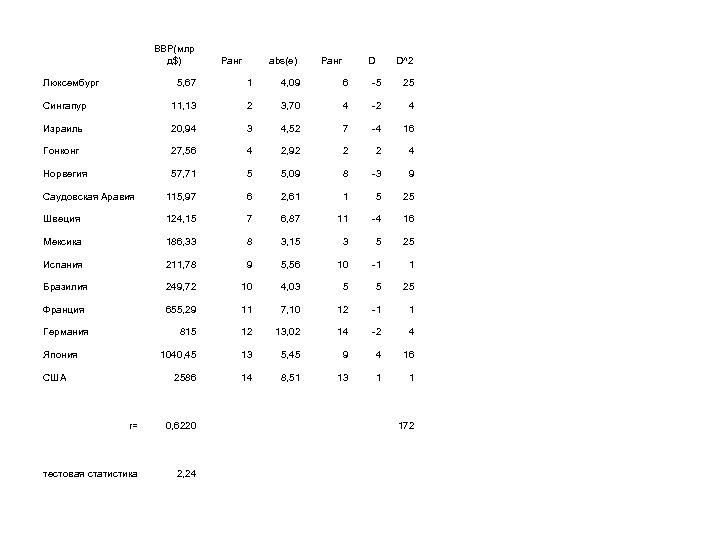BBP(млр д$) Люксембург Ранг abs(e) Ранг D D^2 5, 67 1 4, 09 6 -5 25 Сингапур 11, 13 2 3, 70 4 -2 4 Израиль 20, 94 3 4, 52 7 -4 16 Гонконг 27, 56 4 2, 92 2 2 4 Норвегия 57, 71 5 5, 09 8 -3 9 Саудовская Аравия 115, 97 6 2, 61 1 5 25 Швеция 124, 15 7 6, 87 11 -4 16 Мексика 186, 33 8 3, 15 3 5 25 Испания 211, 78 9 5, 56 10 -1 1 Бразилия 249, 72 10 4, 03 5 5 25 Франция 655, 29 11 7, 10 12 -1 1 815 12 13, 02 14 -2 4 1040, 45 13 5, 45 9 4 16 2586 14 8, 51 13 1 1 Германия Япония США r= 0, 6220 тестовая статистика 2, 24 172

Обнаружение гетероскедастичности (продолжение) • Тест Голфелда-Квандта Предположения: 1) стандартное отклонение распределения ui пропорционально значению x в этом наблюдении 2) случайный член распределен нормально 3) в случайном члене отсутствует автокорреляция Алгоритм: наблюдения упорядочиваются по величине средние (n-2 n/) отбрасываются для первых n/ и для последних n/ оценивается регрессия RSS 2/RSS 1 имеет F-распределение с (n-n/ -2 p): 2 и (n-n/ -2 p): 2 степенями свободы Условия применимости: (n- n/ ): 2>k, если n=30, то n/ порядка 11 если n=60, то n/ порядка 22

Обобщенный МНК • Пусть • Модель примет вид • Перейдем к модели

• Или • (*) • где новая переменная • Теорема Уравнение (*) дает более эффективные оценки, чем исходное уравнение. • Замечание В ОМНК минимизируется взвешенная сумма квадратов • Проблема: нам неизвестны Ki • Возможные пути решения: – приблизительно пропорционально x в парной регрессии или одной из переменных в множественной регрессии

Пример Пусть y-издержки производства, x 1 - объем продукции, x 2 – основные производственные фонды, x 3 – численность работников • Модель издержек производства с объемными факторами y=a+b 1 x 1+b 2 x 2+. . . b 3 x 3+U 1) Если предположим, что пропорциональна квадрату численности работников x 3, то получим в качестве результативного признака затраты на одного работника, а в качестве факторов показатели: производительность труда, фондовооруженность труда. Модель:

2) Если предположим, что пропорциональна квадрату объема производства x 1, то получим в качестве результативного признака затраты на единицу (или на 1 рубль) продукциии, а в качестве факторов показатели: фондоемкость продукции, трудоемкость продукции. Модель: