Georgetown University Last Time Ø The Analytics

Georgetown University

Last Time Ø The Analytics of Profit maximizing Prices Ø The economics of cost pass-throughs

Review Why study pricing? Ø In a market economy, what factors determine prices, in general? Ø In a consideration of prices what is the role of costs? Ø What is the Inverse Elasticity Rule? Ø How does the production of substitutes (complements) affect optimal pricing? Ø In a world in which you control price, how does one determine optimal cost pass-through rates? Ø

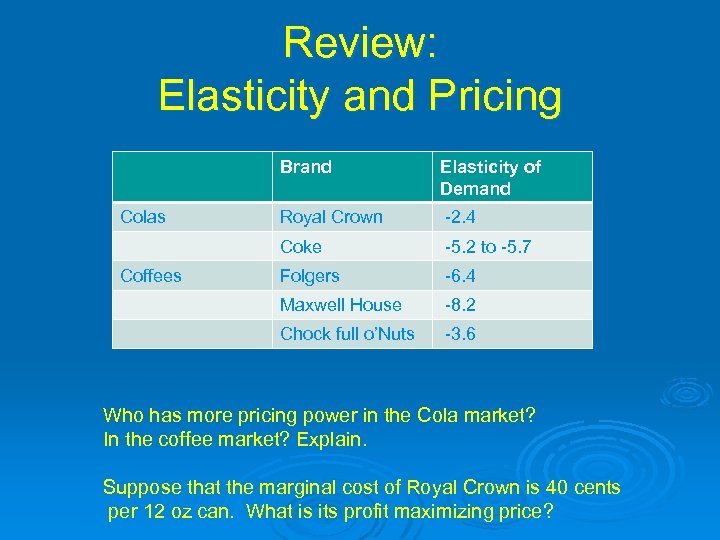Review: Elasticity and Pricing Brand -2. 4 -5. 2 to -5. 7 Folgers -6. 4 Maxwell House -8. 2 Chock full o’Nuts Coffees Royal Crown Coke Colas Elasticity of Demand -3. 6 Who has more pricing power in the Cola market? In the coffee market? Explain. Suppose that the marginal cost of Royal Crown is 40 cents per 12 oz can. What is its profit maximizing price?

How does Coke’s pricing change if it buys Royal Crown? (Pi - ∂C/ ∂qi)/Pi = 1/ εii – [(pj- ∂C/ ∂qj)Qj εij] / Ri εii. 1. 2. 3. 4. 5. The higher is the RC PCM, the higher the price increase The higher are RC volumes, the higher the price increase The higher the cross-price elasticity, the higher the price increase The higher the volume of Coke sales, the lower the price increase The higher the Coke own-price elasticity, the lower the price increase

Coffee bean prices have risen… What should Maxwell House do?

TAKE AWAY ON COST-PASS THROUGH If constant elasticity of demand If linear demand If semi-log demand dp/d. MC = [ε/(1+ ε)] dp/d. MC = ½ dp/d. MC = 1

A Pint-Sized Problem What has been the reaction of beer suppliers to rising input prices?

A Pint-Sized Problem?

The Role of Industrial Organization on Pricing Ø Competition v. Monopoly Ø Strategic Interactions Among Competitors l Oligopoly (Few competitors; Barriers to entry) l Possible reactions to price changes: • Competitors match price decreases, but not price increases l Models: Sweezy oligopoly • Price is determined by market output. Each competitors set output to maximize profit given the output of rivals l Model: Cournot Oligopoly • Firms constantly seek to undercut competitors’ prices l Model: Bertrand oligopoly • Price leadership (One or more firm calls out price and others follow) l Ø Model: Dominant Firm-Competitive fringe Models rely upon Nash equilibrium concept

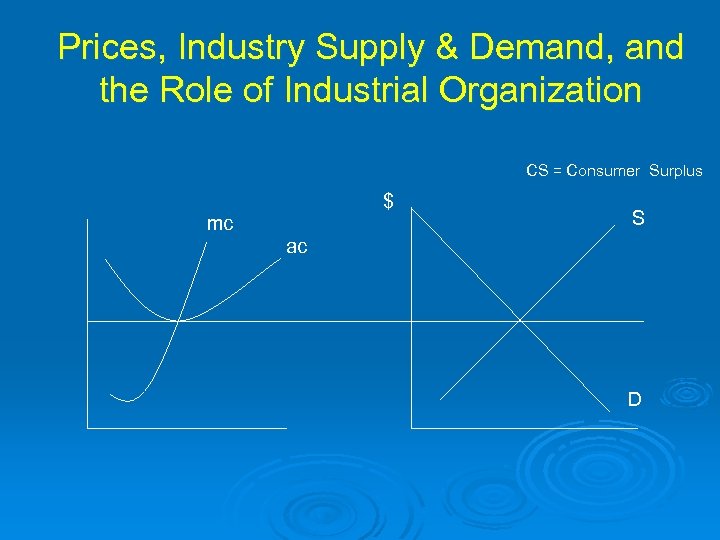Prices, Industry Supply & Demand, and the Role of Industrial Organization CS = Consumer Surplus $ mc S ac D

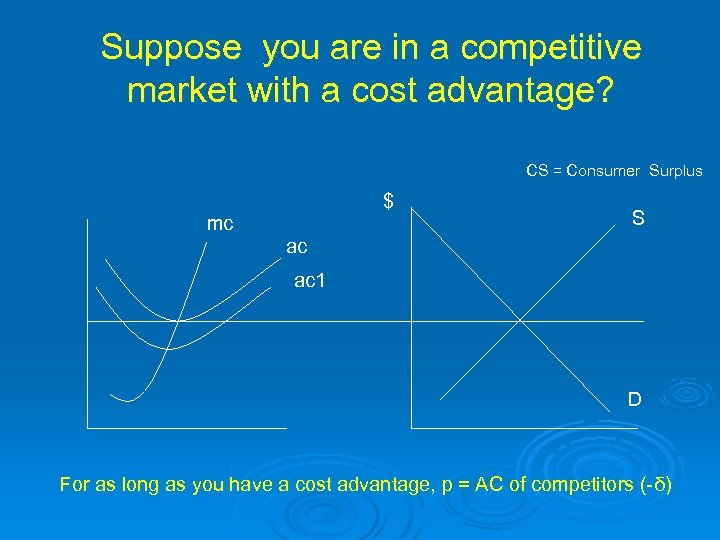Suppose you are in a competitive market with a cost advantage? CS = Consumer Surplus $ mc S ac ac 1 D For as long as you have a cost advantage, p = AC of competitors (-δ)

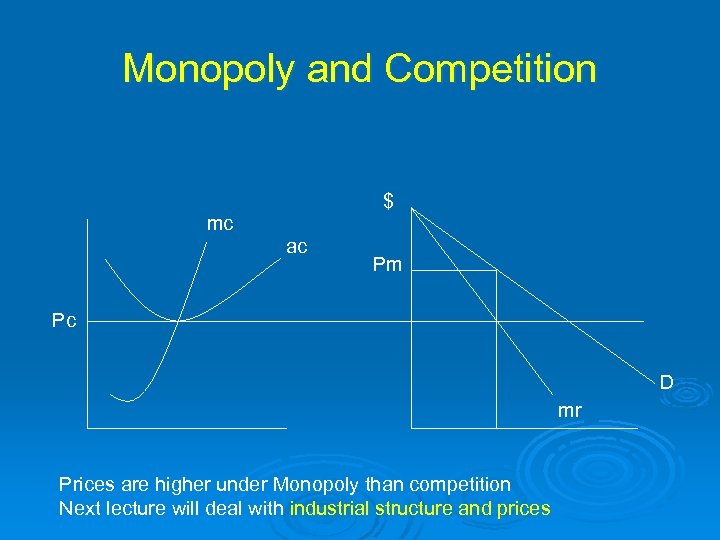Monopoly and Competition $ mc ac Pm Pc D mr Prices are higher under Monopoly than competition Next lecture will deal with industrial structure and prices

The Role of Market Structure in Pricing Ø Suppose that: l l Market Demand Q=1000 -1000 P MC = $. 28 Ø How do optimal prices compare depending on Market Structure and the nature of competition?

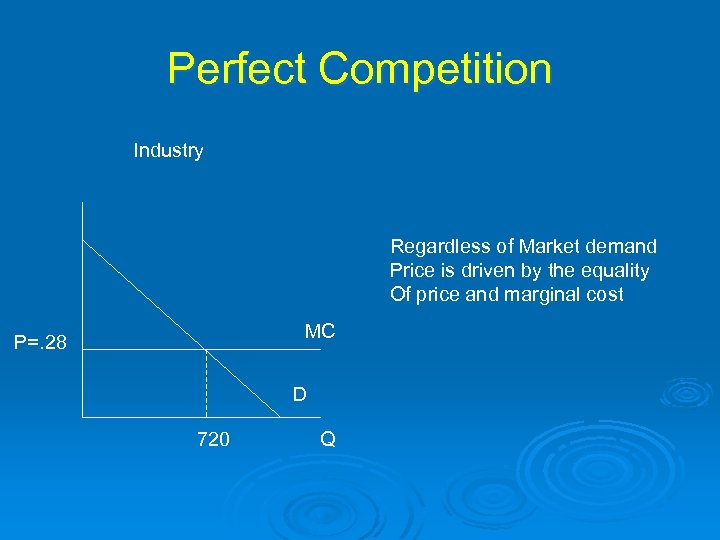Perfect Competition Industry Regardless of Market demand Price is driven by the equality Of price and marginal cost MC P=. 28 D 720 Q

Monopoly Firm π = PQ -. 28 Q π = [1 – (1/1000 Q)]Q -. 28 Q π = Q -. 001 Q 2 -. 28 Q So, taking the first derivative And setting equal to 0: P=. 64 MC P=. 28 D mr 360 720 Dπ/d. Q = 1 -. 002 Q -. 28 =0 Q = 360 Q Plugging into the demand function P=. 64.

The Role of Industrial Organization on Pricing Ø Competition v. Monopoly Ø Strategic Interactions Among Competitors l l l Oligopoly (Few competitors; Barriers to entry) If considering a price change …must consider rivals’ reaction… Possible reactions to price changes: • Competitors match price decreases, but not price increases l Model: Sweezy oligopoly • Price is determined by market output. Each competitors set output to maximize profit given the output of rivals l Model: Cournot Oligopoly • Firms constantly seek to undercut competitors’ prices l Model: Bertrand oligopoly • Price leadership (One or more firm calls out price and others follow) l Model: Dominant Firm-Competitive fringe • Dynamic Pricing: Tit-for Tat Ø Models rely upon Nash equilibrium concept

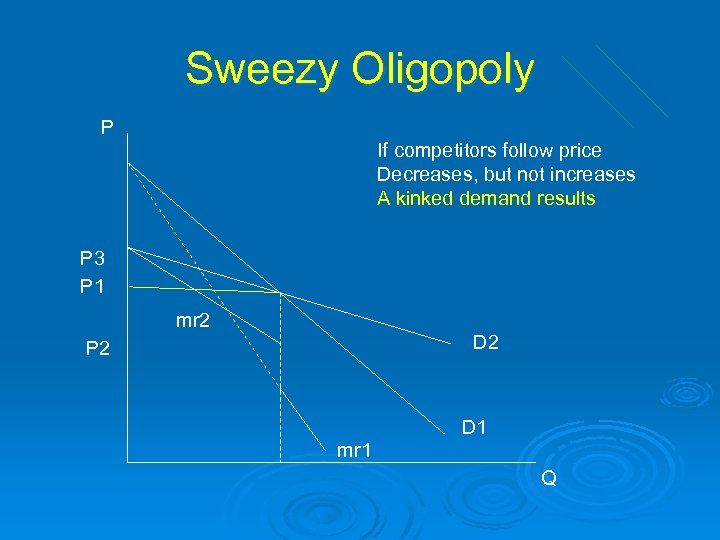Sweezy Oligopoly P If competitors follow price Decreases, but not increases A kinked demand results P 3 P 1 mr 2 D 2 P 2 D 1 mr 1 Q

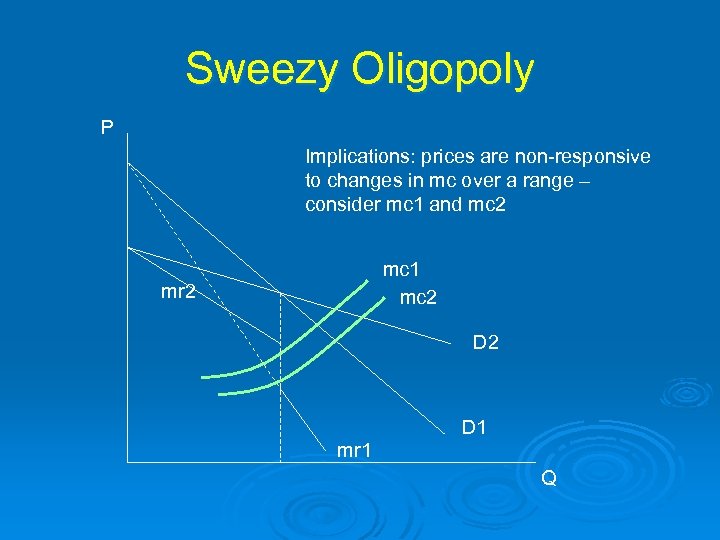Sweezy Oligopoly P Implications: prices are non-responsive to changes in mc over a range – consider mc 1 and mc 2 mc 1 mc 2 mr 2 D 1 mr 1 Q

Nash equilibrium In a Nash equilibrium, each firm is optimizing, given the behavior of other firms John Nash 1994 Nobel Laureate

Cournot Oligopoly Ø Price is determined by total market output (relative to demand) Ø So my strategy must account for the output of rivals l l If duopoly: Q 1* =r 1(Q 2) and Q 2* = r 2(Q 1)

Cournot Model: Nash equilibrium as number of firms changes With an initial equilibrium of Qm, Pm, consider the output of a second firm. The second firm takes the output of Firm 1 as given, then optimizes on the Residual demand curve (the lower Half of the original demand) Pm The result is P 2 What is Firm 1’s reaction? D 1 Qm mr 1 mr 2

Cournot Model: Nash equilibrium as number of firms changes The result is P 2. What is Firm 1’s reaction? Firm 1, then takes the output of firm 2 as given and reduces its output. Why? Because firm 2 has taken ¼ of market. Pm P 2 D 1 mr 2

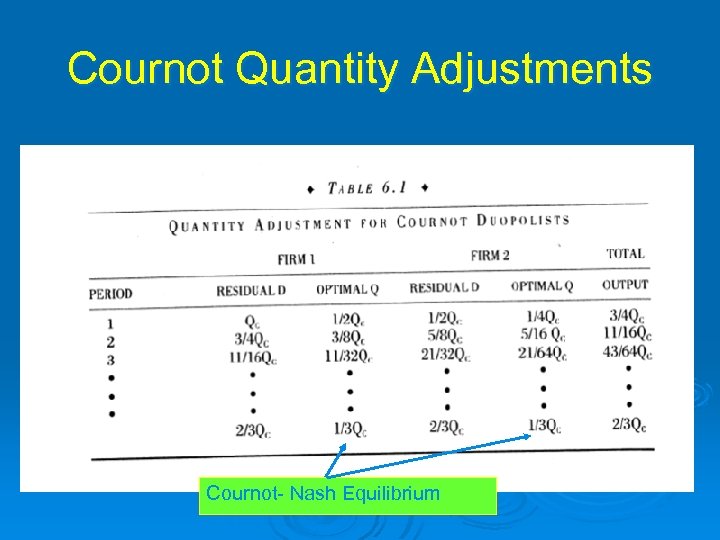Cournot Quantity Adjustments Cournot- Nash Equilibrium

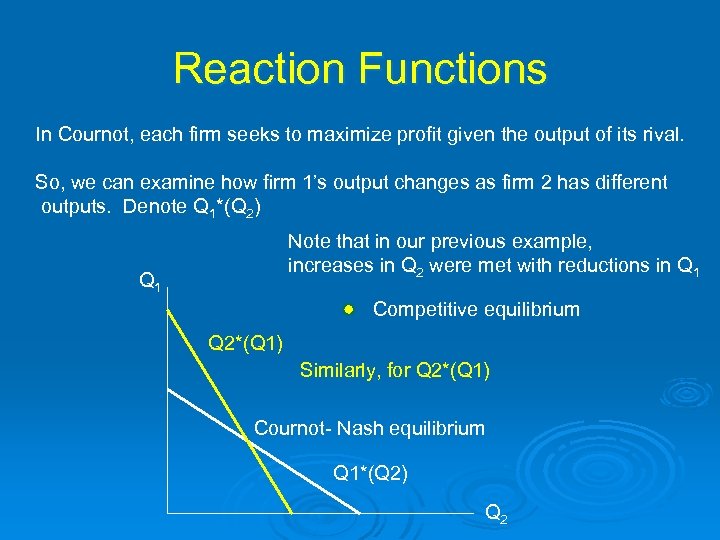Reaction Functions In Cournot, each firm seeks to maximize profit given the output of its rival. So, we can examine how firm 1’s output changes as firm 2 has different outputs. Denote Q 1*(Q 2) Note that in our previous example, increases in Q 2 were met with reductions in Q 1 Competitive equilibrium Q 2*(Q 1) Similarly, for Q 2*(Q 1) Cournot- Nash equilibrium Q 1*(Q 2) Q 2

Cournot: A linear demand example Suppose that market demand is P= 30 -Q and MC 1=MC 2 = 0. What is firm 1’s reaction function? Revenue for firm 1 = PQ 1 = (30 -Q)Q 1 = (30 – Q 1 - Q 2)Q 1 = 30 Q 1 – Q 12 – Q 1 Q 2 Thus, MR = 30 -2 Q 1 -Q 2 Set MR=MC and solve for Q 1: Q 1 = 15 - 1/2 Q 2 Similarly, Q 2 = 15 -1/2 Q 1

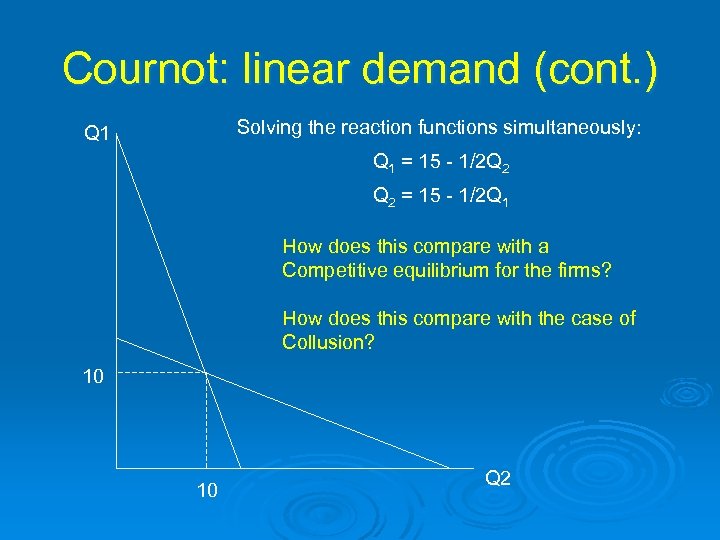Cournot: linear demand (cont. ) Solving the reaction functions simultaneously: Q 1 = 15 - 1/2 Q 2 = 15 - 1/2 Q 1 How does this compare with a Competitive equilibrium for the firms? How does this compare with the case of Collusion? 10 10 Q 2

Price Determination in Cournot Oligopolies Cournot oligopoly (P-MC)/P = s/ε Pricing (where s is market share) Cournot oligopoly w/ Identical frims (P – MC)/P = 1/(nε) Take-aways: 1. Each firm has some market power 2. Cournot prices are “in-between” competitive and monopoly prices 3. Greater elasticity reduces prices 4. Mark-ups are higher for higher market shares (if differentiated) 5. As the number of competitors grows, prices approach competitive levels

Bertrand Oligopoly Ø Assume that firms compete against each other through prices l Homogeneous • Suppose that P= 30 -Q and mc 1 = mc 2 = 3 • Nash Equilibrium? Ø Differentiated Joseph Bertrand

Bertrand Oligopoly Ø Assume that firms compete against each other through prices l Homogeneous • Suppose that P= 30 -Q and mc 1 = mc 2 = 3 • Nash Equilibrium? Ø Differentiated Joseph Bertrand

Differentiated Bertrand Ø Suppose 2 firms each with fixed costs of 20. l l Q 1 = 12 - 2 P 1 +P 2 (demand facing firm 1) Q 2 = 12 – P 2 +P 1 (demand facing firm 2) Find π = P 1 (12 -2 P 1 +P 2 ) Set ∂dπ/ ∂ p 1 = 0, to get firm 1’s reaction function: • P 1 = 3 + 1/4 P 2, and similarly for firm 2, • P 2 = 3 + 1/4 P 1

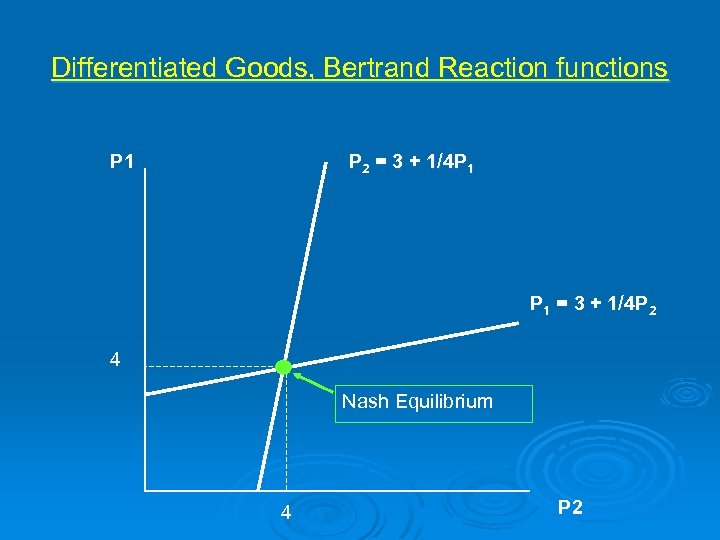Differentiated Goods, Bertrand Reaction functions P 1 P 2 = 3 + 1/4 P 1 = 3 + 1/4 P 2 4 Nash Equilibrium 4 P 2

Cola Wars: Coke and Pepsi Ø Bertrand competition in prices with a differentiated product Ø Rival’s prices do affect the firm’s demand function, but because products are differentiated a lower price does not steal the entire market Ø Each firm has a Bertrand profit-maximizing “best response function” for the price to charge in response to the price its rival charges

Cola Wars: Coke and Pepsi Ø Demand equations estimated from detailed monthly price data: Ø q. C(PC, PP) = 63. 42 – 3. 98 PC + 2. 25 PP Ø q. P(PC, PP) = 49. 52 – 5. 48 PP + 1. 40 PC Ø Unit Cost. C Ø = 4. 96 Unit Cost. P = 3. 96 Unit is a 10 cases of 24 12 oz cans. Source: “Econometric Analysis of Collusive Behavior in a Soft-Drink Market” by Gasmi, Laffont and Vuong in Journal of Economics & Management Strategy, 1992, vol. 1, issue 2, pp. 277 -311

Cola Wars: Coke and Pepsi Ø How should Coke and Pepsi price in response to their rival? Ø Need to find Best Response Function for each cola producer Ø Solve for profit-maximizing PRICE (in a Bertrand game price is the choice variable)

Cola Wars: Coke and Pepsi Ø How do we find profit-maximizing price? Set MR = MC!! Ø Solve for MR (in terms of change in PC): Ø TRC = PC * q. C(PC, PP) Ø TRC = PC * (63. 42 – 3. 98 PC + 2. 25 PP) Ø MRC(PC, PP) = 63. 42 – (2)* 3. 98 PC + 2. 25 PP Ø MRC = 63. 42 – 7. 96 PC + 2. 25 PP Ø

Cola Wars: Coke and Pepsi Ø How do we find profit-maximizing price? Set MR = MC!! Ø Solve for MR (in terms of change in PC): Ø TRC = PC * q. C(PC, PP) Ø TRC = PC * (63. 42 – 3. 98 PC + 2. 25 PP) Ø MRC(PC, PP) = 63. 42 – (2)* 3. 98 PC + 2. 25 PP Ø MRC = 63. 42 – 7. 96 PC + 2. 25 PP Ø

Cola Wars: Coke and Pepsi Ø Solve for MC (again, in terms of PC): Ø TCC = UCC * q. C(PC, PP) Ø TCC = 4. 96 * (63. 42 – 3. 98 PC + 2. 25 PP) Ø MCC(PC, PP) = -19. 74 (MC with respect to PRICE – if price goes up, quantity goes down)

Cola Wars: Coke and Pepsi Ø Profit maximizing price is where MR = MC Ø MRC = 63. 42 – 7. 96 PC + 2. 25 PP Ø MCC = -19. 74 Ø MRC = MCC Ø 63. 42 – 7. 96 PC + 2. 25 PP = -19. 74 Ø PC(PP) = 10. 44 + 0. 2826 PP Ø “Best Response Function”

Cola Wars: Coke and Pepsi Ø Can do the same thing for Pepsi -Ø Best Response Function for Pepsi Ø PP(PC) = 6. 49 + 0. 1277 PC Ø PC(PP) = 10. 44 + 0. 2826 PP Ø 2 equations and 2 unknowns: Ø PC(PP) = 10. 44 + 0. 2826 *(6. 49 + 0. 1277 PC) Ø PC(PP) = 12. 73; PP(PC) = 8. 11 Ø Actual average prices over this period: C=12. 96, P=8. 16

Price Determination Competitive P=MC Competitive w/ cost advantage P=MC(competitors) - δ Monopoly Pricing: (P-MC)/P = 1/ε Cournot oligopoly (P-MC)/P = s/ε Pricing (where s is market share) Cournot oligopoly w/ Identical firms (P – MC)/P = 1/(nε) Bertrand (identical product) P=MC Bertrand Differentiated P> MC

Price Leadership The Dominant Firm Model a. Assumes a single “dominant” firm facing a competitive “fringe” b. The dominant firm calls out a price c. The competitive fringe responds as a price taker setting its output

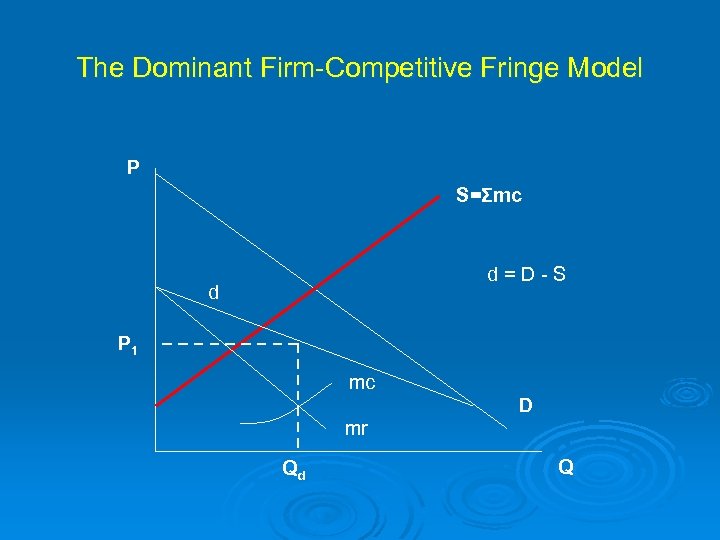The Dominant Firm-Competitive Fringe Model P S=Σmc d=D-S d P 1 mc D mr Qd Q

Pricing in a Dominant Firm Competitive Fringe Industry (P-MC)/P = S/[ηm + (1 -S)ef] 1. Market share (S) 2. Elasticity of Market demand (ηm) 3. Elasticity of Supply of the fringe firms (ef) Suppose S=. 8, ηm = 2, and ef = 2, What is the value of the price cost mark up?

Collusion

Price Collusion “People of the same trade seldom meet together even for merriment and diversion, but the conversation ends in a conspiracy against the public, or in some contrivance to raise prices. ” Adam Smith The Wealth of Nations

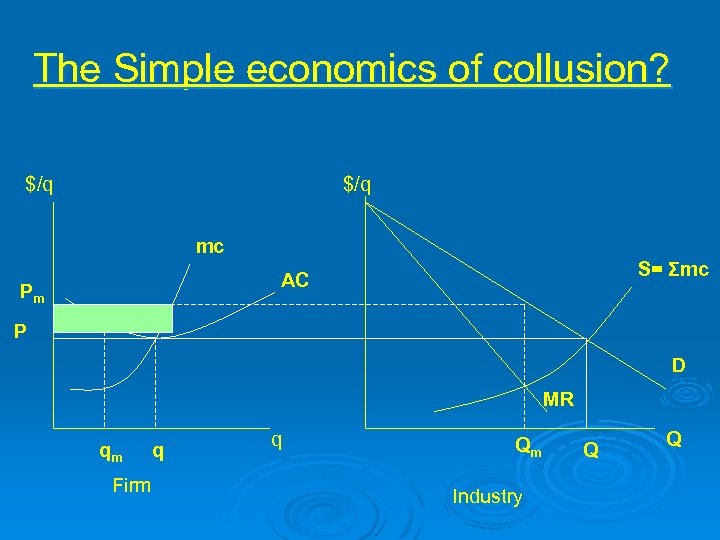The Simple economics of collusion? $/q mc S= Σmc AC Pm P D MR qm q Firm q Qm Industry Q Q

Competition (? ) in the Airline Industry Crandall: I think it's dumb as hell. . . to sit here and pound the (deleted) out of each other and neither one of us making a (deleted) dime. . We can both live here [Dallas] and there ain't no room for Delta. But there's, ah, no reason that I can see, all right, to put both companies out of business. Putnam: Do you have a suggestion for me? Crandall: yes, I have a suggestion for you. raise your goddamn fares twenty percent. I'll raise mine the next morning. . You'll make more money, and I will too. Putnam: We can't talk about pricing. Crandall: Oh (deleted), Howard. We can talk about any goddamn thing we want to talk about.

Economic conditions conducive to and destructive of Collusion Ø Number of firms (market concentration) Ø Barriers to entry Ø Product homogeneity Ø Elasticity of market demand Ø Ability to detect cheating Ø Cost symmetry/asymmetry Economic research indicates that despite obstacles, economic barriers to successful collusion can often be overcome

Rebates in Real Estate Commissions “If we give rebates and inducements, it would get out of control and all clients would be wanting something. The present law keeps it under control. ” Ø “This would turn into a bidding war, lessen our profits and cheapen our ‘so-called’ profession. ” Ø “If inducements were allowed, they could lead to competitive behavior, which would make us look unprofessional in the eyes of the public. ” Ø “I think this would just take money right out of our pocket. ” Ø http: //www. usdoj. gov/atr/public/real_estate/rebates. htm