Geometry Ms Toney Orientation Student Information Sheet

Geometry Ms. Toney

Orientation Student Information Sheet n Classroom Rules n Classroom Policies n Calendar n

What you will learn today: n n Identify and model points, lines, and planes. Identify collinear and coplanar points and intersecting lines and planes in space.

Geometry in the Real – World? n n Where are there points, lines, and/or planes in this classroom? What about outside the classroom, like in nature?

Some Important Definitions n Point ¨A location ¨ Drawn as a dot ¨ Named by a capital letter ¨ Has no shape and no size ¨ Example:

Some Important Definitions n Line ¨ Made up of points, has no thickness or width ¨ Drawn with arrowhead at each end ¨ Named by the letters representing two points on the line or a lower case script letter ¨ There is exactly one line through any two points ¨ Example: n Collinear ¨ Points on the same line

Some Important Definitions n Plane ¨ A flat surface made up of ¨ Has no depth and extends points infinitely in all directions ¨ Drawn as a shaded figure ¨ Named by a capital script letter or by the letter naming the three noncollinear points ¨ There is exactly one plane through any three noncollinear points ¨ Points are often used to name lines and planes ¨ Example: n Coplanar ¨ Points that lie on the same plane

Example n Use the figure to name each of the following ¨A line containing point D ¨ A plane containing point B

You Do It n Use the following figure to name each of the following ¨A line containing point K ¨ A plane containing point L

Real – World Examples

Undefined Terms n Point, line and plane are undefined terms ¨ Have only been explained using examples and descriptions ¨ We can still use these to define other geometric terms and properties Two lines intersect at a point n Lines can intersect planes n Planes can also intersect each other n

Example n Draw and label a figure for each relationship Lines GH and JK intersect at L for G(-1, -3), H(2, 3), J(-3, 2), and K(2, -3) on a coordinate plane. Point M is coplanar with these point but not collinear with lines GH or JK. ¨ Line TU lies in a plane Q and contains point R ¨

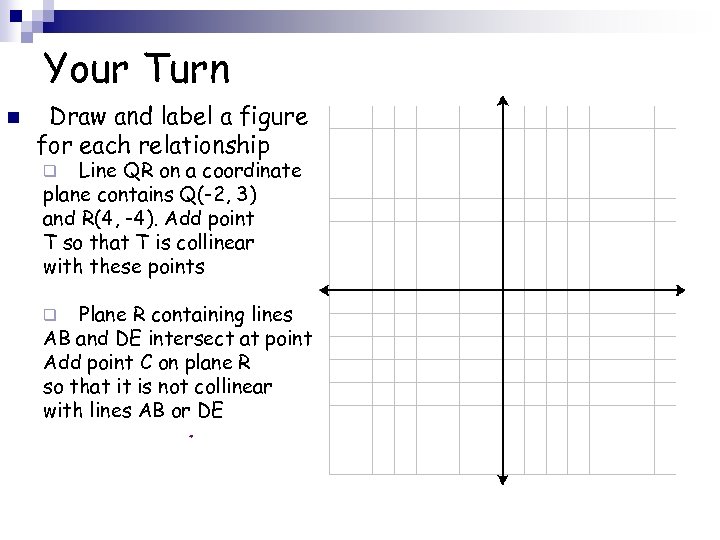Your Turn n Draw and label a figure for each relationship Line QR on a coordinate plane contains Q(-2, 3) and R(4, -4). Add point T so that T is collinear with these points q Plane R containing lines AB and DE intersect at point Add point C on plane R so that it is not collinear with lines AB or DE q

Space A boundless, three – dimensional set of all points n Can contain lines and planes n

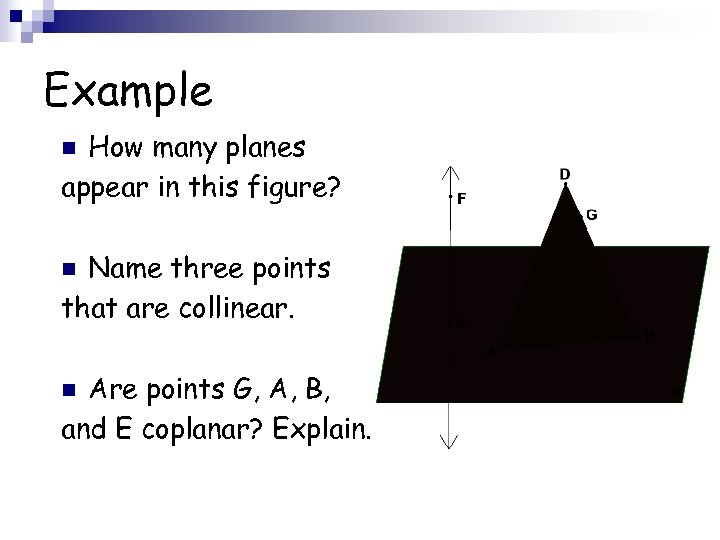Example How many planes appear in this figure? n Name three points that are collinear. n Are points G, A, B, and E coplanar? Explain. n

Example How many planes appear in this figure? n Name three points that are collinear. n n Are points A, B, C, and D coplanar? Explain.

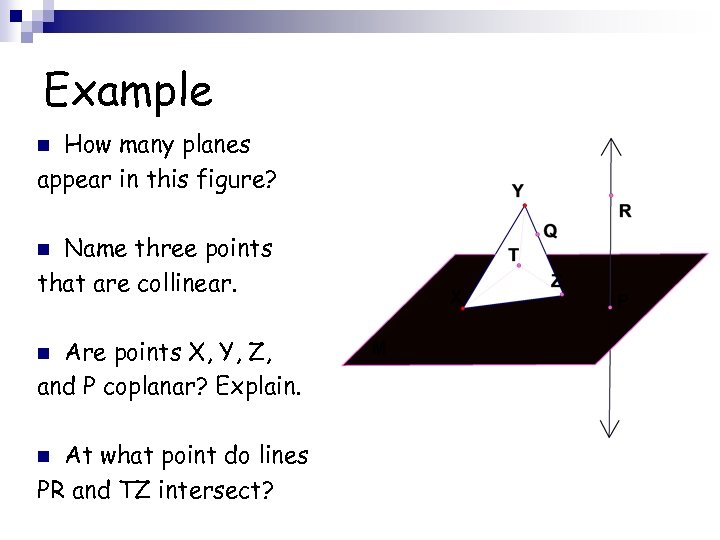Example How many planes appear in this figure? n Name three points that are collinear. n Are points X, Y, Z, and P coplanar? Explain. n At what point do lines PR and TZ intersect? n

Classwork n Worksheet

Homework n Workbook

What you will learn today: n Measure segments. n Find the distance between two points. n Find the midpoint of a segment.

Units of Measure n When you see this sign, what unit of measure do you believe is being used?

Units of Measure Actually in Australia, the unit of measure is kilometers. n Units of measure give us points of reference when evaluating the sizes of objects. n

Measure Line Segments n Line Segment ¨ Also called a segment ¨ Can be measured because it has two endpoints ¨ Named: ¨ The length or measure of is AB. ¨ The length of a segment is only as precise as the smallest unit on the measuring device.

Example n Find AC. n Find DE. n Find y and PQ if P is between Q and R, PQ = 2 y, QR = 3 y + 1, and PR = 21.

Your Turn n Find LM. n Find XZ. n Find x and ST if T is between S and U, ST = 7 x, SU = 45, and TU = 5 x – 3.

More Terms n Congruent ¨ When two segments have the same measure ¨ Segments and angles are congruent ¨ Distant and measures are equal

End of 1. 2

Distance n Is always positive ¨ Because n you use whole numbers Ways to find distance: ¨ Number line ¨ Pythagorean n Theorem c 2 = a 2 + b 2 ¨ Distance Formula

Example n Use the number lines to find the following:

Example

Example

Your Turn

Midpoint n The point halfway between the endpoints of a segment ¨ If B is the midpoint of ¨ Two formulas: n Number Line n Coordinate Plane the AB = BC

Example n n n The coordinates on a number line of J and K are -12 and 16, respectively. Find the coordinate of the midpoint of G(8, -6) and H(-14, 12). for A is an endpoint and B is the midpoint located at A(3, 4) and B(-2, 1). Find the other endpoint C.

Your Turn n n Find coordinates of D if E(-6, 4) is the midpoint of and F has coordinates -5, -3). What is the measure of midpoint of ? if Q is the (

Segment Bisector n A segment, line or plane that intersects a segment at its midpoint

Quiz Time n n Please clear off your desk You will have 20 – 25 minutes to complete your quiz When you are finished turn your quiz in and sit quietly in your sit until everyone has finished We will begin today’s lesson after the quiz

Angle Measure n Ray: ¨ Part of a line ¨ Has one endpoint and extends indefinitely in one direction ¨ Named stating the endpoint first and then any other point on the ray

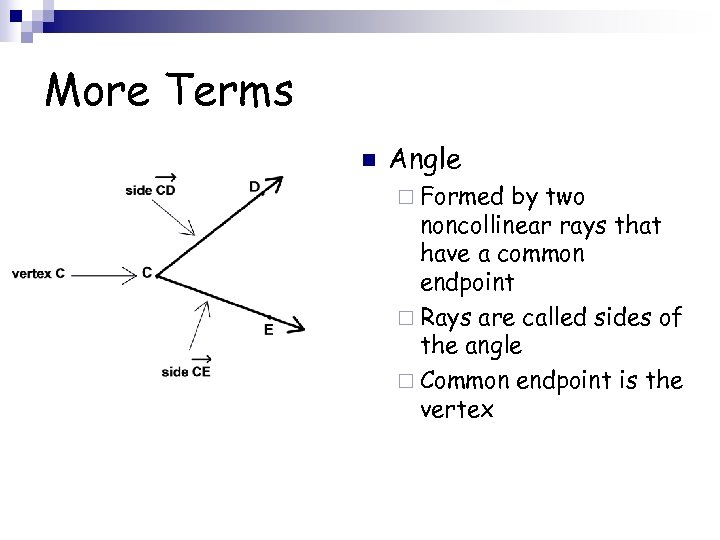More Terms n Angle ¨ Formed by two noncollinear rays that have a common endpoint ¨ Rays are called sides of the angle ¨ Common endpoint is the vertex

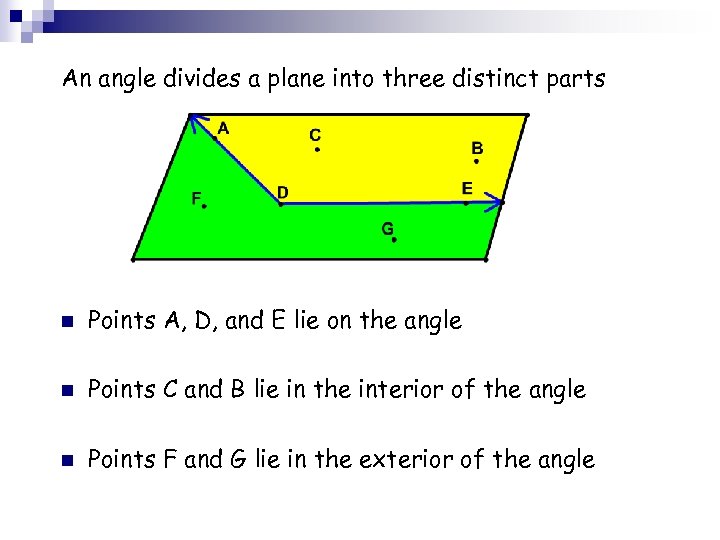An angle divides a plane into three distinct parts n Points A, D, and E lie on the angle n Points C and B lie in the interior of the angle n Points F and G lie in the exterior of the angle

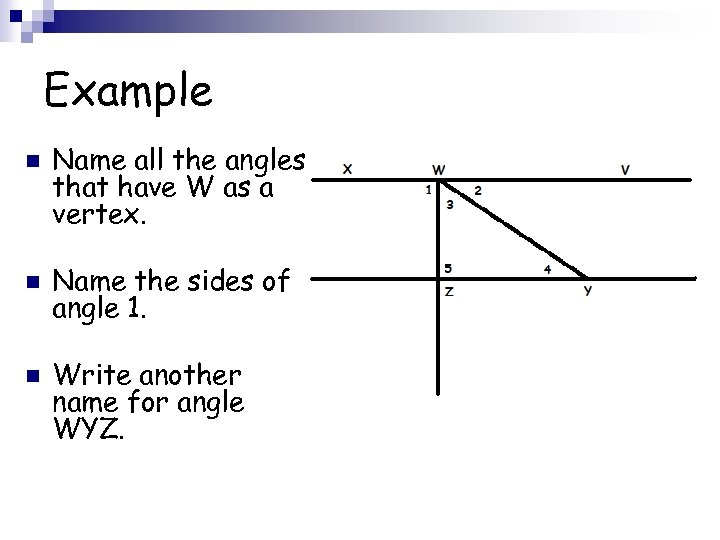Example n n n Name all the angles that have W as a vertex. Name the sides of angle 1. Write another name for angle WYZ.

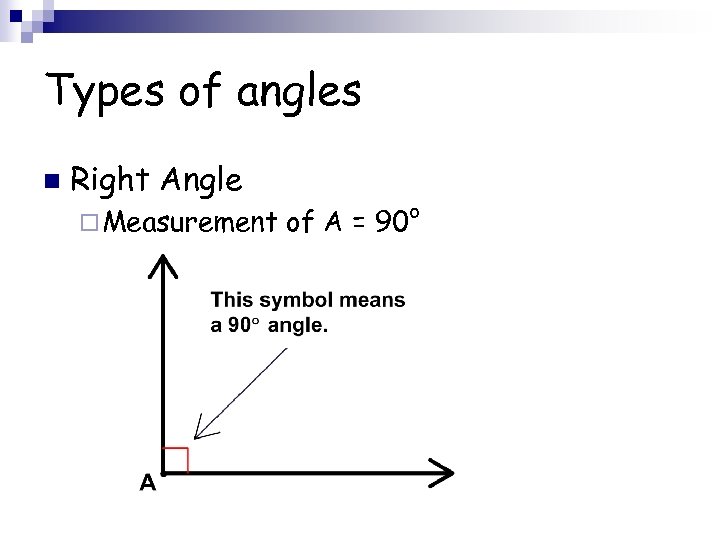Types of angles n Right Angle ¨ Measurement of A = 90°

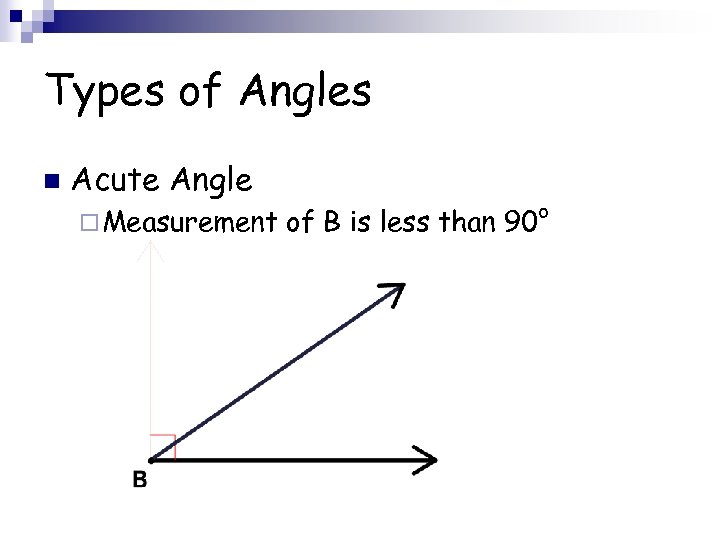Types of Angles n Acute Angle ¨ Measurement of B is less than 90°

Types of angles n Obtuse angles ¨ Measurement of C is less than 180° and greater than 90°

Congruent Angles n Just like segments that have the same measure are congruent, angles that have the same measure are congruent.

Example n Wall stickers of standard shapes are often used to provide a stimulating environment for a young child’s room. Find and , , and

You Do It n A trellis is often used to provide a frame for vining plants. Some of the angles formed by the slats of the trellis are congruent angles. If

Bisectors n Segment Bisector ¨A segment, line or plane that intersects a segment at its midpoint n Angle Bisector ¨A ray that divides an angle into two congruent angles

Warm – Up #3 n Name three different types of angles and describe them. n What is a bisector?

Today you have a choice! n Option 1: ¨ Section n 1. 5 Option 2: ¨ Review of 1. 1 – 1. 4 (lots of work)

Option 2: Review 1. 1 – 1. 4 n Textbook ¨ Pages n 13 -18, 21 – 26, 30 - 35 ¨ Page n 9 - 10 17 12 – 15, 22 – 26, 28 - 32 ¨ Pages 25 n 13 – 16, 23, 24, 31, 32, 37, 38, 43, 44 ¨ Pages n - 26 34 - 35 12 -37, 50

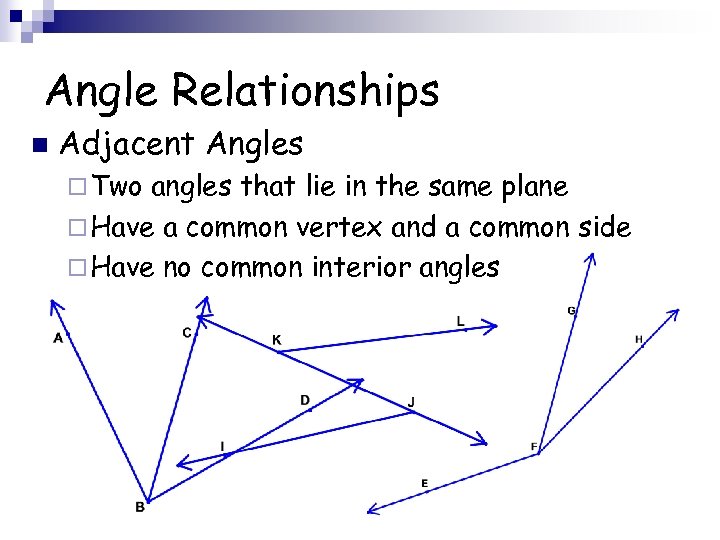Angle Relationships n Adjacent Angles ¨ Two angles that lie in the same plane ¨ Have a common vertex and a common side ¨ Have no common interior angles

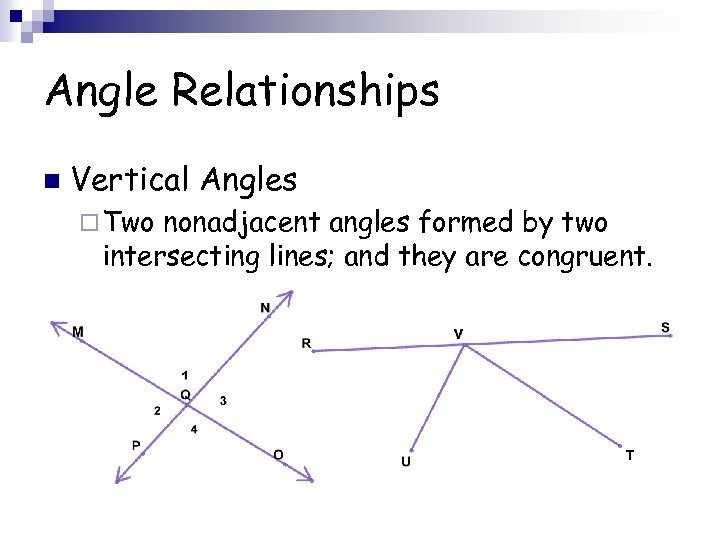Angle Relationships n Vertical Angles ¨ Two nonadjacent angles formed by two intersecting lines; and they are congruent.

Angle Relationships n Linear Pair ¨A pair of adjacent angles whose noncommon sides are opposite rays

Example n Refer to the picture: ¨ Name n n an angle pair that satisfies each condition Two obtuse vertical angles Two acute vertical angles Two angles that form a linear pair Two acute adjacent angles

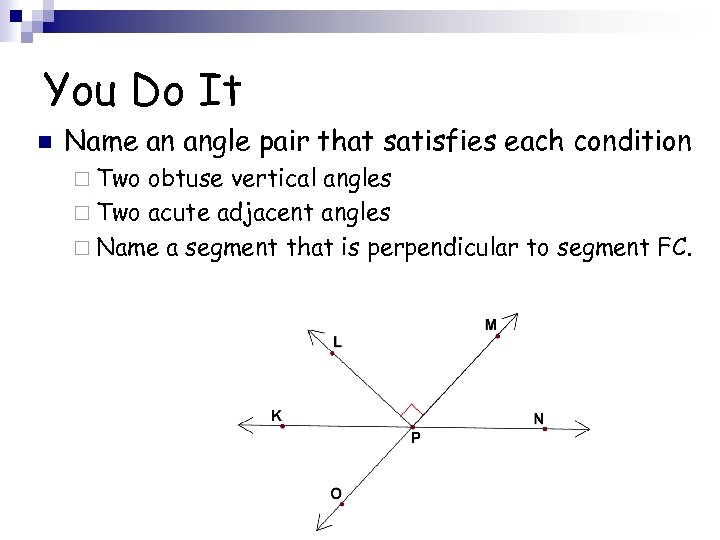You Do It n Name an angle pair that satisfies each condition ¨ Two obtuse vertical angles ¨ Two acute adjacent angles ¨ Name a segment that is perpendicular to segment FC.

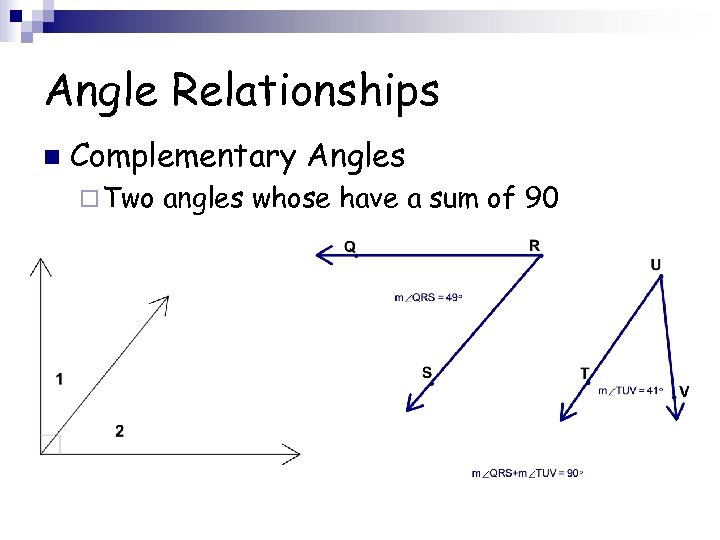Angle Relationships n Complementary Angles ¨ Two angles whose have a sum of 90

Angle Relationships n Supplementary Angles ¨ Two angles whose measures have a sum of 180

Example n Find the measures of two supplementary angles if the measure of one angle is 6 less than five time the measure of the other angle

You Do It n Find the measures of two complementary angles if the difference in the measures of the two angles is 12.

Angle Relationships n Perpendicular Lines ¨ Lines that form right angles ¨ Intersect to form congruent adjacent angles ¨ Segments and rays can be perpendicular to lines or to other line segments and rays ¨ ┴ is read is perpendicular to and this symbol will indicate that two lines are perpendicular

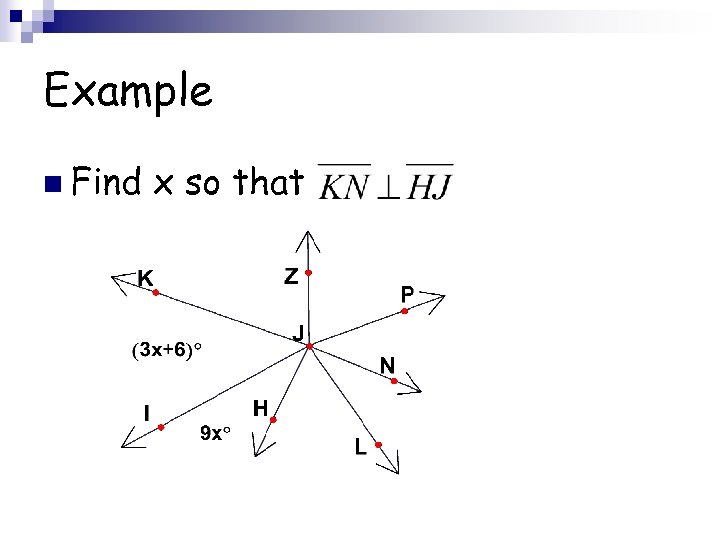Example n Find x so that

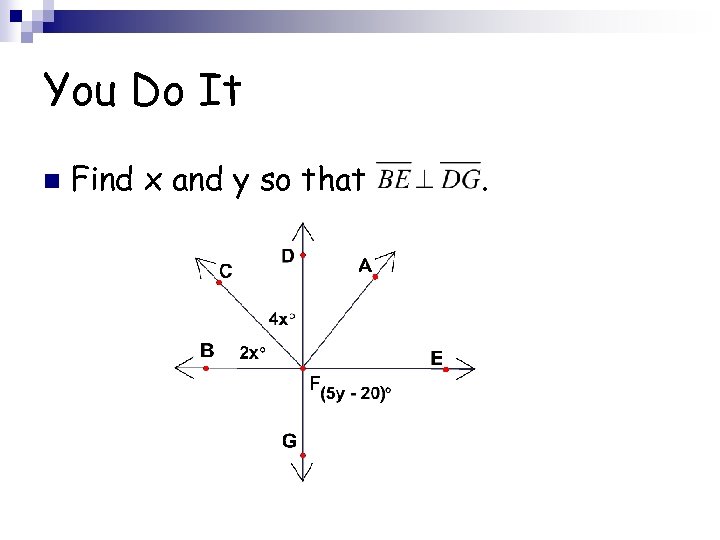You Do It n Find x and y so that .

Things to Remember: n n While two lines may appear to be perpendicular in a figure, you cannot assume this is true unless other information is given. The table on page 40 in your textbook has a list of things that may be assumed and things that may not be assumed.

Click the mouse button or press the Space Bar to display the answers.

Polygon n Is a closed figure formed by a finite number of coplanar segments such that ¨ The sides that have a common endpoint are noncollinear ¨ Each side intersects exactly two other sides, but only at their endpoints n n Named by the letters of its vertices, written in consecutive order Examples:

Concave or Convex? n n Polygons can be concave or convex. How do we know which one? ¨ Suppose the line containing each side is drawn. ¨ If any of the lines contain any point in the interior of the polygon, then it is concave. ¨ Otherwise it is convex. ¨ Example:

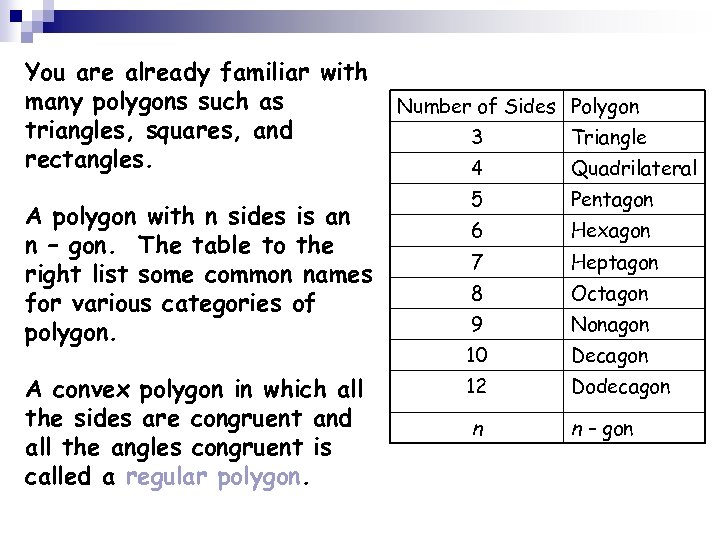You are already familiar with many polygons such as triangles, squares, and rectangles. A polygon with n sides is an n – gon. The table to the right list some common names for various categories of polygon. A convex polygon in which all the sides are congruent and all the angles congruent is called a regular polygon. Number of Sides Polygon 3 Triangle 4 Quadrilateral 5 Pentagon 6 Hexagon 7 Heptagon 8 Octagon 9 Nonagon 10 Decagon 12 Dodecagon n n – gon

Example n Name each polygon by its number of sides. Then classify it as convex or concave and regular or irregular.

Your Turn n Name each polygon by its number of sides. Then classify it as convex or concave and regular or irregular.

Perimeter The sum of the lengths of its sides, which are segments. n Some shapes have special formulas, but they all come from the basic definition of perimeter. n ¨ Triangle: P=a+b+c ¨ Square: P = s + s + s = 4 s ¨ Rectangle: P = l + w + l + w = 2 l + 2 w

Example n A landscape designer is putting black plastic edging around a rectangular flower garden that has length 5. 7 meters and width 3. 8 meters. The edging is sold in 5 -meter lengths. ¨ Find the perimeter of the garden and determine how much edging the designer should buy. ¨ Suppose the length and width of the garden are tripled. What is the effect on the perimeter and how much edging should the designer buy?

Your Turn n A masonry company is contracted to lay three layers of decorative brick along the foundation for a new house given the dimensions below. ¨ Find the perimeter of the foundation and determine how many bricks the company will need to complete the job. Assume that one brick is 8 inches long. ¨ The builder realizes he accidentally halved the size of the foundation in part a, so he reworks the drawing with the correct dimensions. How will this affect the perimeter of the house and the number of bricks the masonry company needs?

Example using the Distance Formula n n Find the perimeter of triangle PQR if P(-5, 1), Q(-1, 4), and R(-6, -8). Find the perimeter of pentagon ABCDE with A(0, 4), B(4, 0), C(3, -4), D(-3, -4), and E(-3, 1).

Your Turn n Find the perimeter of quadrilateral PQRS with P(-3, 4), Q(0, 8), R(3, 8), and S(0, 4).

Perimeter to Find Sides n The length of a rectangle is three times the width. The perimeter is 2 feet. Find the length of each side

Your Turn n The width of a rectangle is 5 less than twice its length. The perimeter is 80 centimeters. Find the length of each side.

Homework n Workbook ¨ Lesson n 1 - 13 1. 6