Geometry 9 Jan 2013 1 Please empty your

Geometry 9 Jan 2013 1) Please empty your group folders. 2) Place your text and binder on your desk. 3) WARM UPLook at Example A on page 423 in your textbook. Be ready to explain how you can find the area of the shape to a 8 year old.

Objective Students will derive formulas for area of rectangles, parallelograms and triangles. Students will take notes, participate in a whole class investigation using think-pair-share. Homework Due Friday pg. 425: 1 - 15 odds, 17, 18, 20, 21 (use graph paper) 1) 2) 3) 4) For all area problems, use the following format: Write the formula Substitute values Do the calculation/ check Add UNITS

Announcement ACCESS TESTING / AP Practice Tests on Thursday. (READ ACCESS talking points from administration. ) This is a very important test that must be taken by students who speak two or more languages. If you are not sure if you need to take this test, check the lists that are posted in the hallways. Other students? No school on Thursday

Class Expectations Supplies- pencil, paper, binder & text to every class (comp book for notes- optional) Start of Class- tardy policy Warm Up- Classwork NORMS Group folders Electronics End of Class

Homework Expectations Start by writing the given information show any sketches; write down the problem What do you KNOW? Clearly write what you are trying to find SHOW ALL WORK clear and concise; EASY for someone else to follow Area/ volume: 1) formula 2) substitute 3) calculate 4) units Underline or box your ANSWER. VALID attempt for all problems. √ or X – check all problems and make corrections

what is area? when do we need to calculate area in life? How much paint do you need to paint a room? How much carpet do I need to buy for my house? How much might it cost to resurface the track at South High School? (track was redone a few summers ago) HOW DO WE CALCULATE AREA?

read page 422 – 424 together Highlights: 1) Area is SQUARE units. You can find area by counting squares! 2) Base can be ANY SIDE! 3) Base height ALWAYS BASE IS ALWAYS PERPENDICULAR to the height! 4) The altitude is the perpendicular distance between opposite sides. It can be inside or outside a parallelogram. The height should be

see page 423 - add to your vocabulary area- the measure of the size of the interior of a figure measured in square units (in 2, cm 2, etc. ) base- ANY side of a polygon used for reference to determine an altitude height- the length of altitude of a parallelogram- a perpendicular segment from a base to the parallel base or line containing that base (see page 424) BASE AND HEIGHT ARE ALWAYS perpendicular!!!

Investigation--We will use think-pair-share to explore area formulas. Parallelograms: 1) Each person in your group needs to cut out ONE parallelogram. 2) Cut your parallelogram along the height so you have 2 pieces. 3) Rearrange the two pieces to make a familiar shape. Is the area of the two pieces the same as the area of the “uncut” parallelogram? 4) What is the formula for finding the area of a parallelogram?

Triangles 1) Each person needs to cut out two triangles with the same letters. 2) DO NOT cut the triangles along “h” line as we did for parallelograms. Simply rearrange the triangles to form a familiar shape for which you already know the area. 3) what is the formula for finding the area of a triangle?

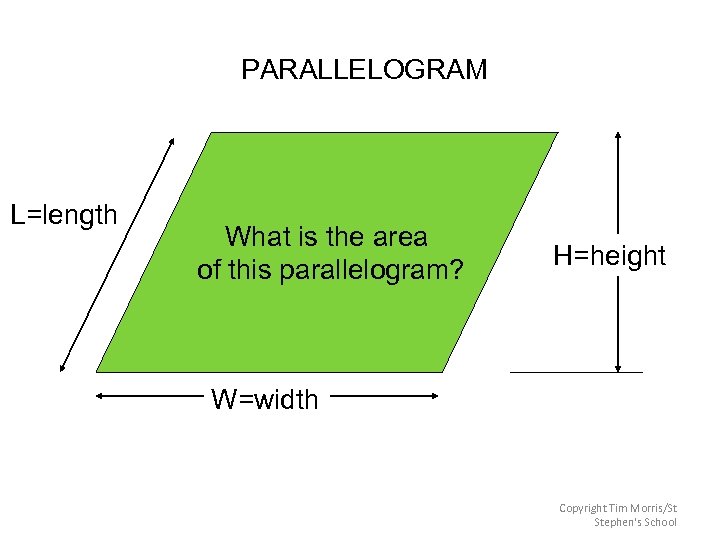PARALLELOGRAM L=length What is the area of this parallelogram? H=height W=width Copyright Tim Morris/St Stephen's School

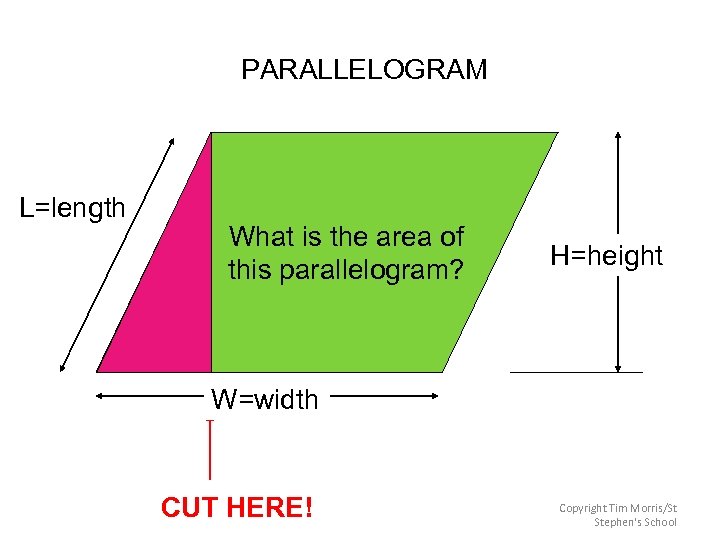PARALLELOGRAM L=length What is the area of this parallelogram? H=height W=width CUT HERE! Copyright Tim Morris/St Stephen's School

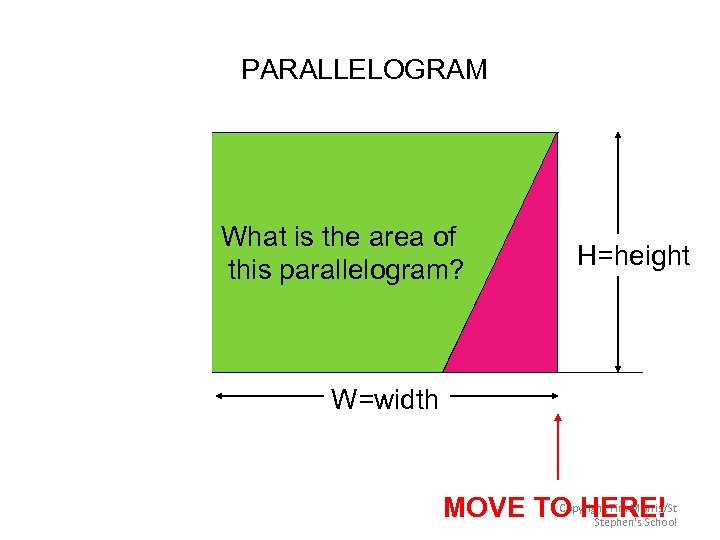PARALLELOGRAM What is the area of this parallelogram? H=height W=width Copyright Tim Morris/St MOVE TO HERE! Stephen's School

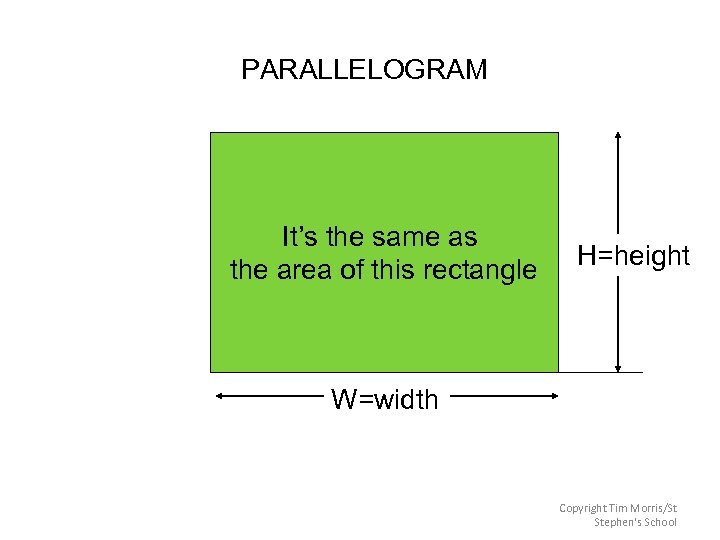PARALLELOGRAM It’s the same as the area of this rectangle H=height W=width Copyright Tim Morris/St Stephen's School

PARALLELOGRAM Arearectangle= Width x Height H=height (perpendicular height H) W=width Copyright Tim Morris/St Stephen's School

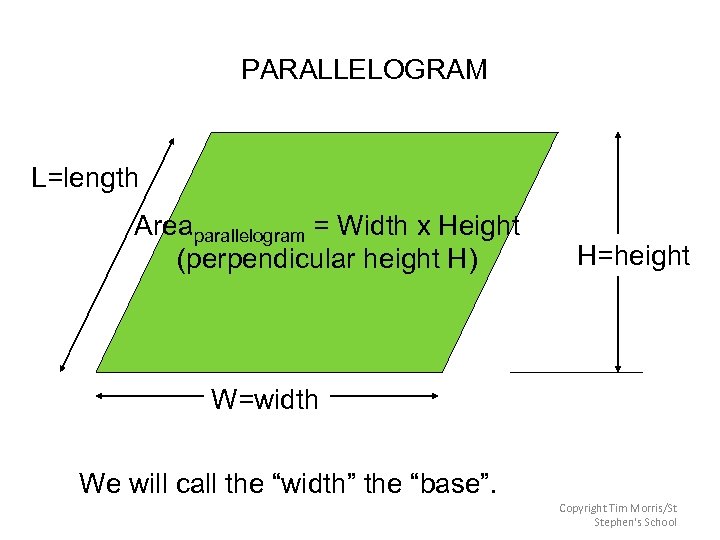PARALLELOGRAM L=length Areaparallelogram = Width x Height (perpendicular height H) H=height W=width We will call the “width” the “base”. Copyright Tim Morris/St Stephen's School

Parallelogram Area Conjecture: The area of a parallelogram is given by the formula A = bh, where A is the area, b is the length of the base and h is the height of the parallelogram. h b

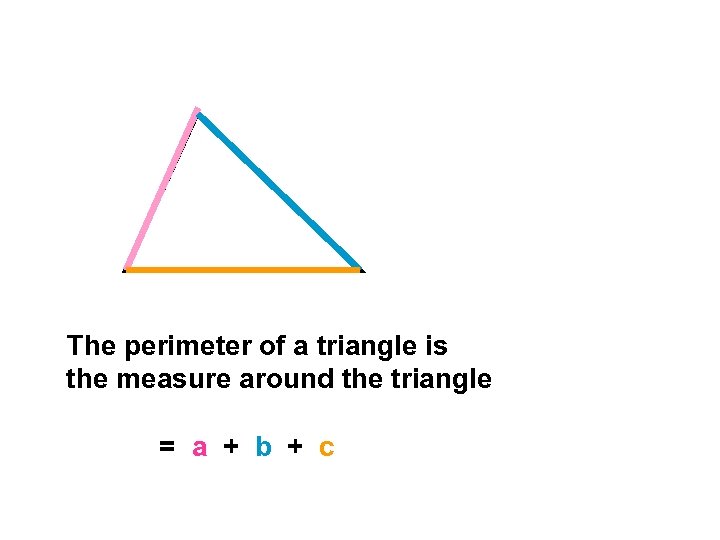The perimeter of a triangle is the measure around the triangle = a + b + c

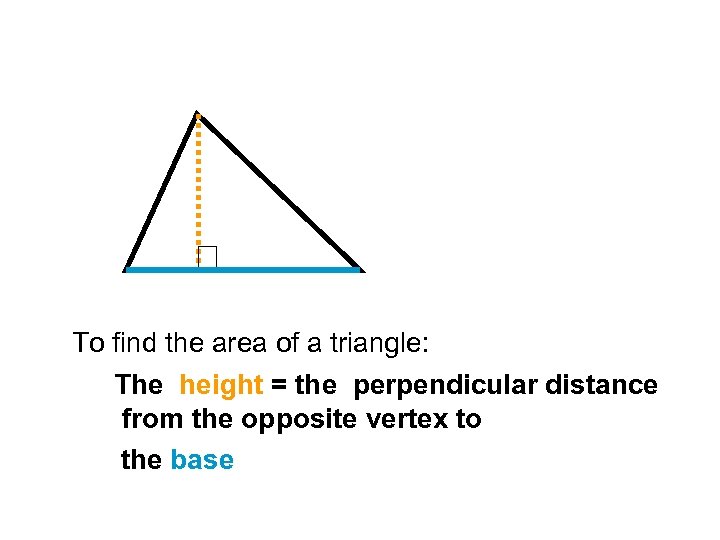To find the area of a triangle: The height = the perpendicular distance from the opposite vertex to the base

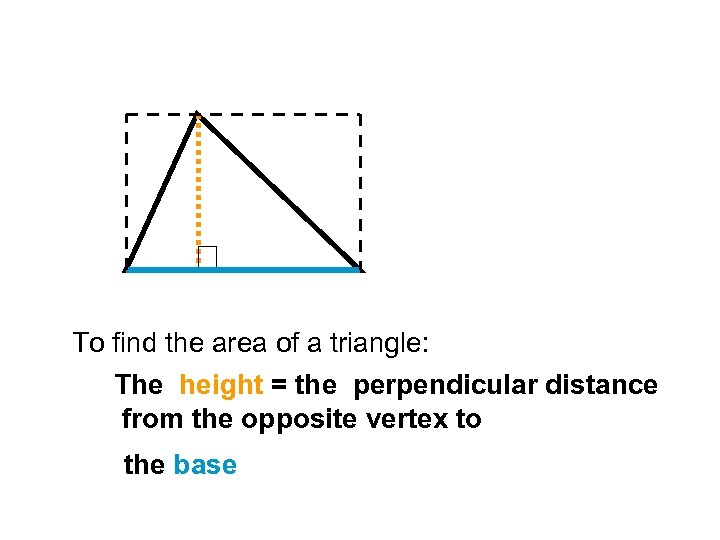To find the area of a triangle: The height = the perpendicular distance from the opposite vertex to the base

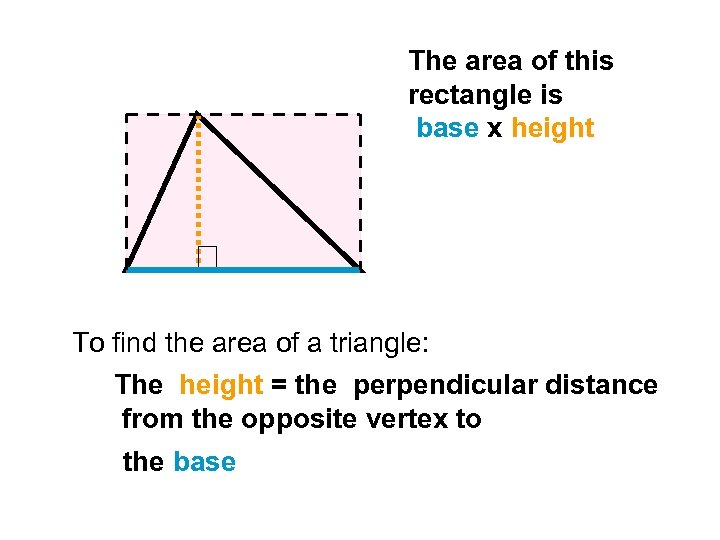The area of this rectangle is base x height To find the area of a triangle: The height = the perpendicular distance from the opposite vertex to the base

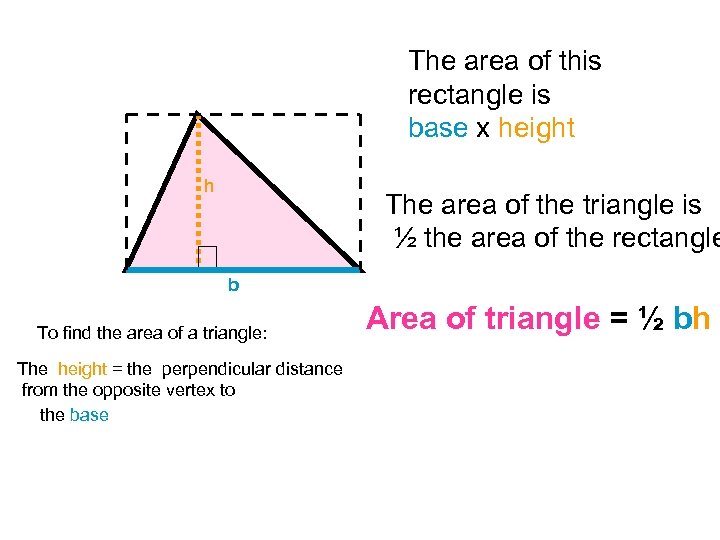The area of this rectangle is base x height h The area of the triangle is ½ the area of the rectangle b To find the area of a triangle: The height = the perpendicular distance from the opposite vertex to the base Area of triangle = ½ bh

Add to Chapter 8 Area Formulas Graphic Organizer Shape Area Formula Definition of Variables Rectangle A = bh b = base (any side) h = height (perpendicular to base) (same as above) b = base (any side) h = height (altitude from base) Parallelogram A = bh Triangle A = ½ bh

debrief How did we derive (come up with) the formula for finding the area of a parallelogram? How did we derive the formula for finding the area of a triangle? What are the formulas for finding the area of a rectangle, parallelogram and triangle?