ГЕОМЕТРИЯ СТРАННЫХ АТТРАКТОРОВ И ИХ РАЗМЕРНОСТИ Рассмотрим

ГЕОМЕТРИЯ СТРАННЫХ АТТРАКТОРОВ И ИХ РАЗМЕРНОСТИ

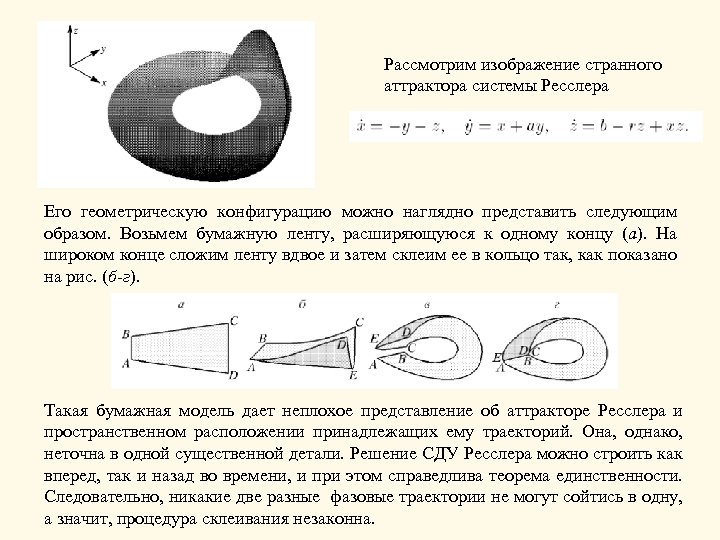Рассмотрим изображение странного аттрактора системы Ресслера Его геометрическую конфигурацию можно наглядно представить следующим образом. Возьмем бумажную ленту, расширяющуюся к одному концу (а). На широком конце сложим ленту вдвое и затем склеим ее в кольцо так, как показано на рис. (б-г). Такая бумажная модель дает неплохое представление об аттракторе Ресслера и пространственном расположении принадлежащих ему траекторий. Она, однако, неточна в одной существенной детали. Решение СДУ Ресслера можно строить как вперед, так и назад во времени, и при этом справедлива теорема единственности. Следовательно, никакие две разные фазовые траектории не могут сойтись в одну, а значит, процедура склеивания незаконна.

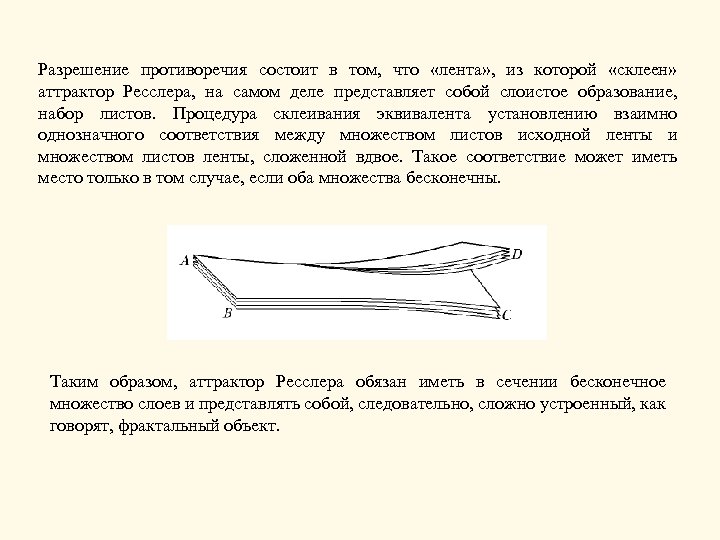Разрешение противоречия состоит в том, что «лента» , из которой «склеен» аттрактор Ресслера, на самом деле представляет собой слоистое образование, набор листов. Процедура склеивания эквивалента установлению взаимно однозначного соответствия между множеством листов исходной ленты и множеством листов ленты, сложенной вдвое. Такое соответствие может иметь место только в том случае, если оба множества бесконечны. Таким образом, аттрактор Ресслера обязан иметь в сечении бесконечное множество слоев и представлять собой, следовательно, сложно устроенный, как говорят, фрактальный объект.

Такой же характер структуры свойственен и другим странным аттракторам. На рисунке приведена диаграмма из статьи Эно, иллюстрирующая структуру аттрактора в отображении (2). Можно отметить, что основной момент в мотивации этой работы как раз и состоял в намерении представить более наглядный для рассмотрения пример фрактальной структуры аттрактора, нежели демонстрировала известная к тому времени модель Лоренца. Воспроизведение фрактальной структуры аттрактора Эно на разных масштабах разрешения

Фракталы Под фракталами понимают множества, демонстрирующие на разных масштабах разрешения своей геометрической структуры свойства подобия (или масштабной инвариантности) в строгом или приближенном смысле, а также объекты в природе, обладающие этим свойством, хотя бы приближенно, в достаточно широком интервале масштабов. Понятие фрактала вошло в обиход благодаря математику Бенуа Мандельброту для обозначения нетривиальных геометрических объектов. Он обратил внимание на то, что фрактальные объекты могут рассматриваться не только как «математические монстры» , но как модели геометрических свойств вполне реальных образований в природе (береговая линия, облака, горные массивы, деревья, вихри в турбулентной жидкости и т. д. ). Классификация фракталов 1. Конструктивные (построенные с помощью определенных рекурсивных геометрических или алгебраических процедур). 2. Динамические (порождаемые динамическими системами). 3. Естественные (наблюдаемые в природе). 4. Стохастические (траектория движения броуновской частицы или произвольная траектория диффузионного случайного процесса).

Простейший конструктивный фрактал связан с построением, предложенным еще в 1883 г. основоположником теории множеств Георгом Кантором. Имея единичный отрезок, разделим его на три равные части и выбросим интервал, занимающий среднюю треть. Каждый из оставшихся отрезков вновь делим на три части и выбрасываем среднюю треть, и так далее до бесконечности. То, что останется в итоге, и есть множество Кантора или «канторова пыль» . Множество Кантора удовлетворяет определению фрактала: каждый его фрагмент, полученный из какого-то отрезка на некотором уровне построения, подобен всему множеству и переходит в него при соответствующем пересчете масштаба. Отметим два свойства множества Кантора. 1) Это множество имеет нулевую меру (нулевую длину), т. е. суммарная длина всех выброшенных интервалов равна 1, длине исходного интервала. На 1 -м шаге выбрасывается интервал длины 1/3, на 2 м – два интервала длины 1/9, на n-м – 2 n интервалов длины 3 -n+1. Вычисляя сумму, получаем

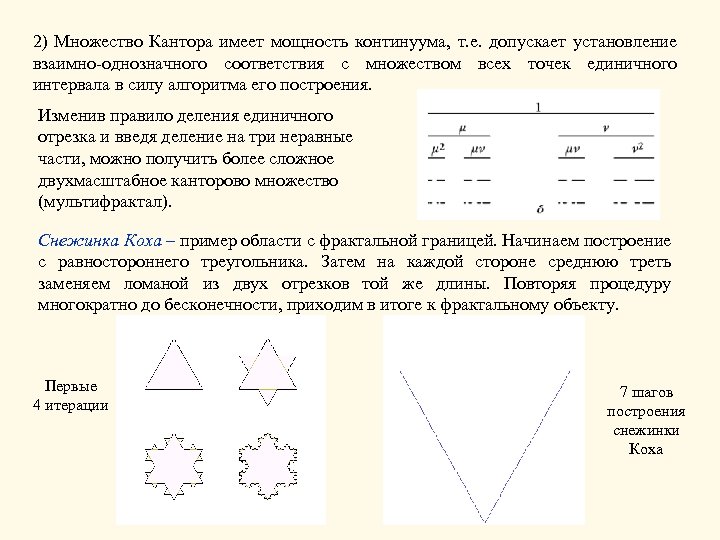2) Множество Кантора имеет мощность континуума, т. е. допускает установление взаимно-однозначного соответствия с множеством всех точек единичного интервала в силу алгоритма его построения. Изменив правило деления единичного отрезка и введя деление на три неравные части, можно получить более сложное двухмасштабное канторово множество (мультифрактал). Снежинка Коха – пример области с фрактальной границей. Начинаем построение с равностороннего треугольника. Затем на каждой стороне среднюю треть заменяем ломаной из двух отрезков той же длины. Повторяя процедуру многократно до бесконечности, приходим в итоге к фрактальному объекту. Первые 4 итерации 7 шагов построения снежинки Коха

Чтобы построить салфетку (треугольник) Серпинского, берем равносторонний треугольник, который можно представить как составленный из четырех меньших треугольников. Средний треугольник выбрасываем. Далее те же действия выполняем с каждым из оставшихся треугольников до бесконечности. Ковер Серпинского строится, исходя из квадрата, который делим вертикальными и горизонтальными линиями на 9 равных частей, и средний квадрат выбрасываем. С каждым оставшимся квадратом ту же процедуру, и так до бесконечности.

Если вынимать середину из куба, то можно получить губку Менгера, каждая грань которого представляет собой ковер Серпинского.

Тетрикс (tetrix) – трехмерный аналог треугольника Серпинского

Фракталы, порождаемые детерминированной динамикой нелинейных систем, называются динамическими. Динамическими фракталами могут быть аттракторы или иные предельные множества в фазовом пространстве, размерность которого N для потоков должна быть N > 2, а для систем с дискретным временем N 2. Когда говорят о нерегулярных аттракторах, то разделяют понятия «странный» и «хаотический» . Именно свойство «странности» относится к его нетривиальной (фрактальной) геометрии. Фрактальными свойствами обладают границы бассейнов притяжения нескольких сосуществующих аттракторов и это является характерной чертой нелинейных ДС.

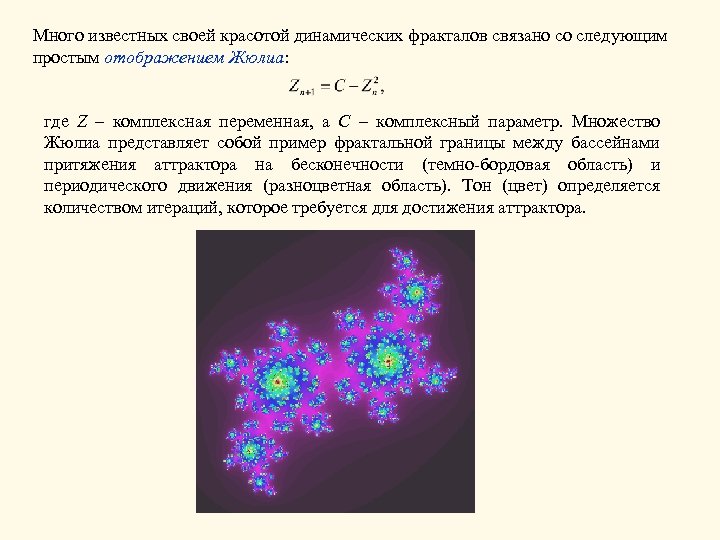Много известных своей красотой динамических фракталов связано со следующим простым отображением Жюлиа: где Z – комплексная переменная, а C – комплексный параметр. Множество Жюлиа представляет собой пример фрактальной границы между бассейнами притяжения аттрактора на бесконечности (темно-бордовая область) и периодического движения (разноцветная область). Тон (цвет) определяется количеством итераций, которое требуется для достижения аттрактора.

Множество Мандельброта Данная фрактальная структура получается путем многократного применения алгебраического преобразования (рекуррентного соотношения) с использованием функции комплексного переменного. Черный цвет в середине показывает, что в этих точках функция стремится к нулю - это и есть множество Мандельброта. За пределами этого множества функция стремится к бесконечности. Cамое интересное - это границы множества. Они то и являются фрактальными. На границах этого множества функция ведет себя непредсказуемо - хаотично.

Размерности аттракторов Отличительная особенность странных аттракторов состоит в наличии свойства масштабной инвариантности (скейлинга), выражающегося в повторяемости их структуры на все более мелких масштабах. Следствием закономерностей подобия является универсальность в геометрии хаотических множеств сечений Пуанкаре, в распределении энергии колебаний по частотам и амплитудам в спектре и т. д. Для характеристики странных аттракторов введено понятие размерности. Размерность определяет количество информации, необходимое для задания координат точки, принадлежащей аттрактору, в рамках указанной точности. Для регулярных аттракторов, являющихся многообразиями, размерность – целое число: неподвижная точка имеет размерность 0, предельный цикл – 1, двумерный тор – 2. Ввиду сложности геометрической структуры странные аттракторы не являются многообразиями и имеют дробную размерность. Определения размерности в общем разделяются на два типа: зависящие только от метрических свойств аттрактора и, помимо метрики, зависящие от статистических свойств потока, обусловленных динамикой. В типичных случаях метрические размерности принимают одинаковую величину, которую принято называть фрактальной размерностью аттрактора D. Размерность, определяемую с учетом вероятности посещения траекторией различных областей аттрактора в фазовом пространстве, называют информационной или размерностью натуральной меры.

Фрактальная размерность - емкость а б

(29)

Применив определение (29) для вычисления размерности точки, линии и поверхности, можно убедиться в привычных значениях 0, 1 и 2 соответственно. Для нетривиальных множеств фрактальная размерность всегда дробная. Это свойства используется как характерный признак «странности» аттрактора. Фрактальную размерность, определенную с помощью покрытия множества ячейками фиксированной формы и размера, называют емкостью множества. Если в качестве покрытия множества используются элементы произвольной формы и размера, то вычисляемая таким образом размерность называется размерностью Хаусдорфа. Для фракталов эта размерность и емкость совпадают и говорят просто о фрактальной размерности объекта.

Информационная размерность Наряду с фрактальной размерностью вводят и используют ряд других, в том числе информационную, корреляционную, обобщенные размерности Реньи. Почему же одной метрической размерности недостаточно? Представим себе, что аттрактор неоднороден – одни области (элементы покрытия) посещаются чаще, другие реже. Это обстоятельство никак не отражено в определении емкости. Пусть для аттрактора определена инвариантная мера, и мы построили покрытие этого аттрактора, тогда как каждая ячейка покрытия будет иметь свою определенную величину меры. Иными словами, каждой i-й ячейке покрытия будет отвечать некоторая вероятность пребывания в ней pi. Считая, что ячейки полностью покрывают аттрактор и не накладываются друг на друга, имеем Рассмотрим теперь сумму (30) Эту величину можно интерпретировать как количество информации в утверждении, что изображающая точка обнаружена в одной определенной ячейке покрытия.

Ясно, что при уменьшении размера ячеек покрытия величина суммы (30) будет возрастать: чем мельче ячейки, тем больше информации в утверждении, что точка попала в данную определенную ячейку. Это нарастание следует закону (31) или, что эквивалентно, существует предел (32) Величину DI называют информационной размерностью.

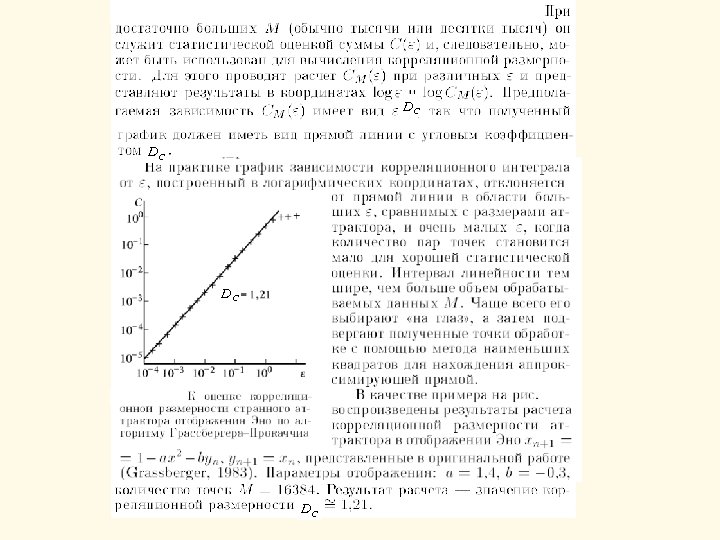
Корреляционная размерность и алгоритм Грассбергера-Прокаччиа Рассмотрим снова покрытие аттрактора ячейками одинакового размера и предположим, что выбраны наугад две точки, принадлежащие аттрактору, x 1 и x 2. Какова вероятность того, что обе они окажутся в i-й ячейке? Вероятность того, что одна точка попадает в i-й элемент покрытия, равна pi. Если попадание обеих точек в данную ячейку можно считать независимыми событиями, то вероятность будет pi 2. Рассмотрим сумму (33) При уменьшении размера ячеек сумма будет убывать и происходить это будет по степенному закону (34) или, что эквивалентно, существует предел (35) Величину DC называют корреляционной размерностью.

(36)

DC DC

Обобщенная размерность Можно обобщить размерности DF , DI , DC и ввести размерность порядка q, пользуясь обобщенной энтропией порядка q (энтропией Реньи) (37) где Pi – вероятность обнаружения точки множества в i-м элементе покрытия. Тогда размерность порядка q есть (38) Можно показать, что D 0 = DF , D 1 = DI , D 2 = DC.

Ляпуновская размерность Фрактальную размерность аттрактора ДС в фазовом пространстве RN можно оценить с помощью спектра ляпуновских характеристических показателей (ЛХП). Такая оценка называется ляпуновской размерностью DL и задается определенным соотношением, называемым формулой Каплана-Йорке. Пусть известен спектр ЛХП странного аттрактора N-мерной системы, размерность которого нужно оценить: 1 2 … N. Сумма всех показателей спектра отрицательна в силу диссипативности системы. Рассмотрим первые k показателей спектра ЛХП, где k – наибольшее число, удовлетворяющее условию В указанное число показателей включены все положительные, все нулевые и некоторая часть отрицательных, чтобы сумма оставалась неотрицательной. Поскольку сумма показателей задает характер локального изменения элемента фазового объема в аттракторе, то фазовый объем размерности k < N в среднем не уменьшается. Увеличение размерности подпространства на единицу приведет в среднем уже к сжатию элемента объема

Таким образом, можно предположить, что размерность аттрактора заключена в интервале k DL k + 1. Разумно потребовать, чтобы движение на аттракторе подчинялось условию, отвечающему физическим представлениям о стационарности процесса, где d – дробная часть размерности. Полная ляпуновская размерность аттрактора будет суммой целой k и дробной d частей: (39) Различия в сигнатуре спектров ЛХП и размерность DL могут быть признаком классификации регулярных и странных аттракторов. Из формулы Каплана-Йорка (39) для регулярных аттракторов получаем следующие значения ляпуновской размерности, совпадающие с фрактальной размерностью соответствующего множества и равные числу нулевых показателей в спектре ЛХП: • состояние равновесия (-, -, -, …) – DL = 0; • предельный цикл (0, -, -, -, …) – DL = 1; • двумерный тор (0, 0, -, -, …) – DL = 2; • N-мерный тор (0, 0, 0, …, 0, -, …) – DL = N.

Для регулярных аттракторов в полном соответствии находятся: ляпуновская размерность, фрактальная размерность и сигнатура спектра ЛХП аттрактора. В отношении странных аттракторов о подобном взаимодействии можно говорить лишь применительно к трехмерным дифференциальным системам и двумерным обратимым отображениям с постоянным растяжением и сжатием. Было доказано, что для аттракторов в таких системах фрактальная размерность может быть определена следующими соотношениями: - для двумерных отображений - для трехмерных дифференциальных систем В общем случае имеет место следующее соотношение между размерностями: Однако в пределах ошибок вычислений можно приближенно считать, что значения размерностей совпадают. При выборе, каким определением размерности лучше воспользоваться, обычно исходят из возможностей численных расчетов. При численном моделировании ДС наиболее удобно использовать размерность Ляпунова. Для оценки фрактальной размерности аттрактора по экспериментальным данным лучше всего подходит корреляционная размерность.