“Геометрия на бумаге” Автор: Иоффе Кристина Вадимовна Руководитель: Анохина Светлана Владимировна
Цели проекта • Узнать о приемах решения задач на клетчатой бумаге. • Вывести формулу геометрической фигуры (трапеции) на клетчатой поверхности с помощью различных способов.
• Основная формула площади трапеции • Существует несколько способов вывести ее: 1) Достроение • 2) Перекраивание • 3) Разрезание
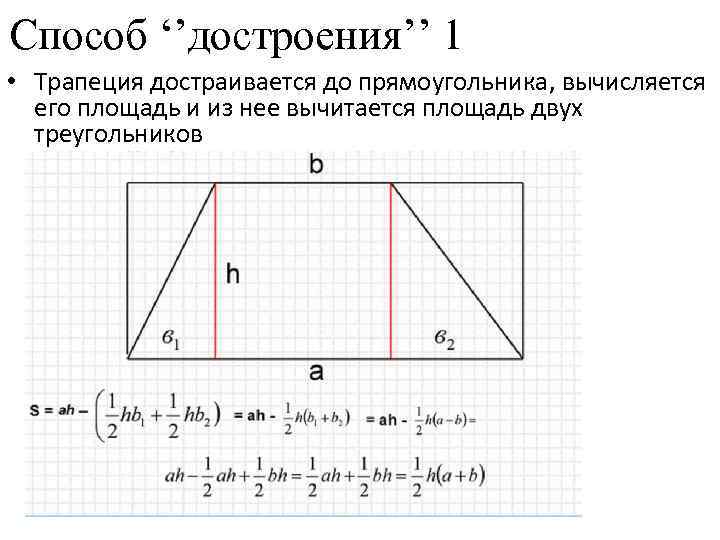
Способ ‘’достроения’’ 1 • Трапеция достраивается до прямоугольника, вычисляется его площадь и из нее вычитается площадь двух треугольников
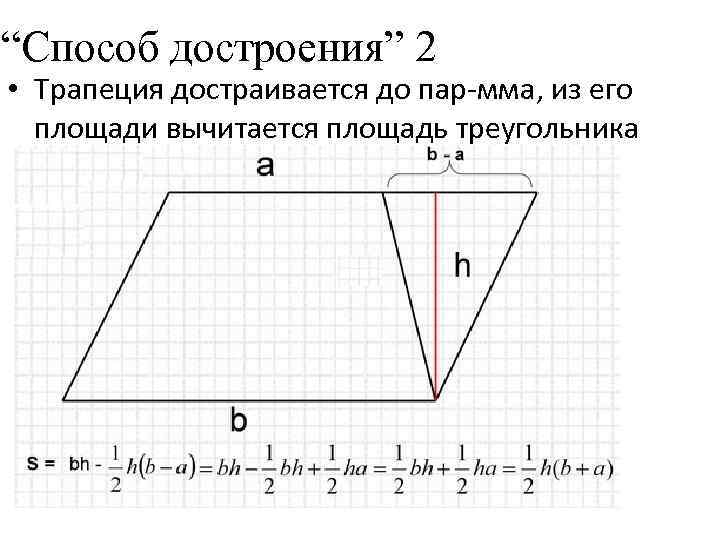
“Способ достроения” 2 • Трапеция достраивается до пар-мма, из его площади вычитается площадь треугольника
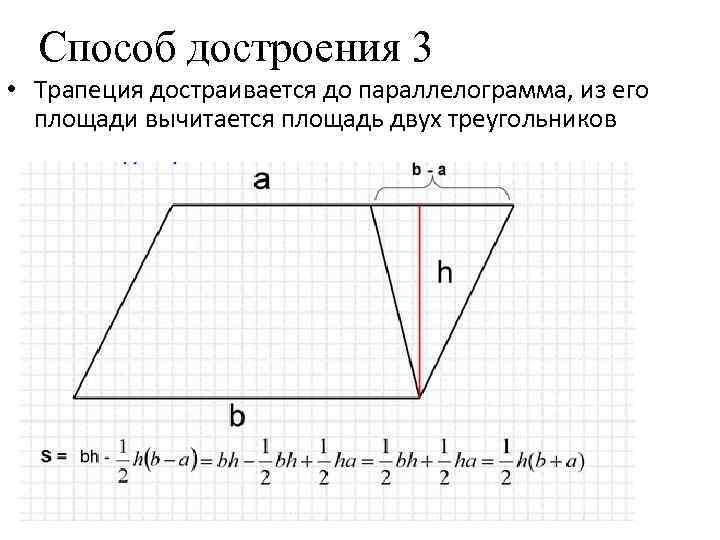
Способ достроения 3 • Трапеция достраивается до параллелограмма, из его площади вычитается площадь двух треугольников
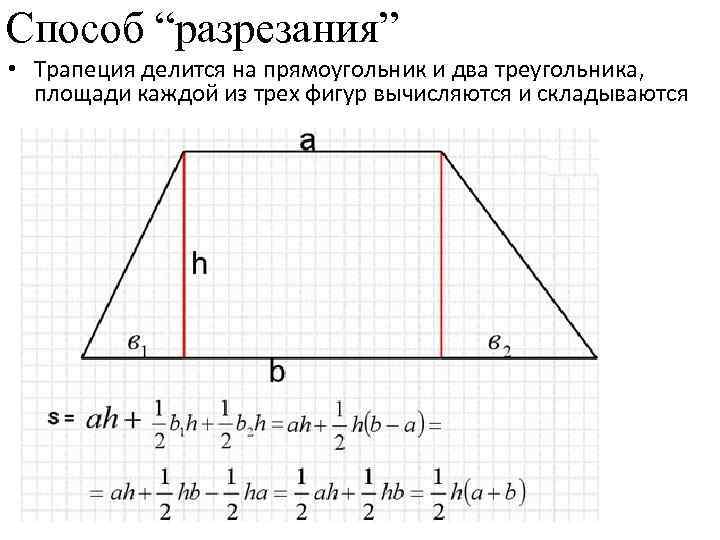
Способ “разрезания” • Трапеция делится на прямоугольник и два треугольника, площади каждой из трех фигур вычисляются и складываются
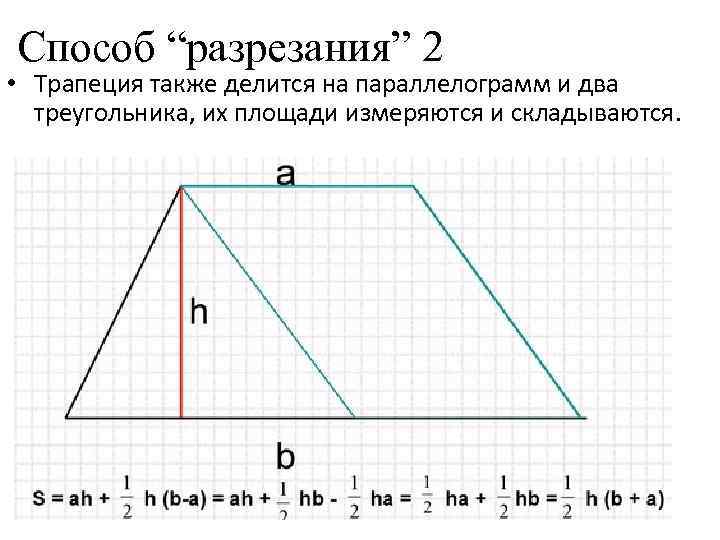
Способ “разрезания” 2 • Трапеция также делится на параллелограмм и два треугольника, их площади измеряются и складываются.
Перекраивание • В обычной формуле площади трапеции полусумма оснований умножается на высоту, переделав формулу, можно получить формулу, по которой площадь трапеции будет равна произведению суммы оснований и полувысоты (h/2)
Вывод • В результате этой работы, доказано, что площадь геометрической фигуры на клетчатой поверхности можно найти множеством способов. Это подтверждает факт, что “Геометрия на клетчатой бумаге” эффективнее, чем “Геометрия на простой бумаге”
Скачать презентацию Геометрия на бумаге Автор Иоффе Кристина Вадимовна Руководитель
Kristina_8a.pptx