Геометрия Многоугольники Параллелограмм Свойства и признаки параллелограмма

Геометрия Многоугольники. Параллелограмм. Свойства и признаки параллелограмма.

Многоугольники • • • Параллелограмм Прямоугольник Ромб Квадрат Трапеция

Параллелограммом называется четырёхугольник, у которого противолежащие стороны попарно параллельны. В С АВIICD, BCIIAD =>ABCD – пар-м А D

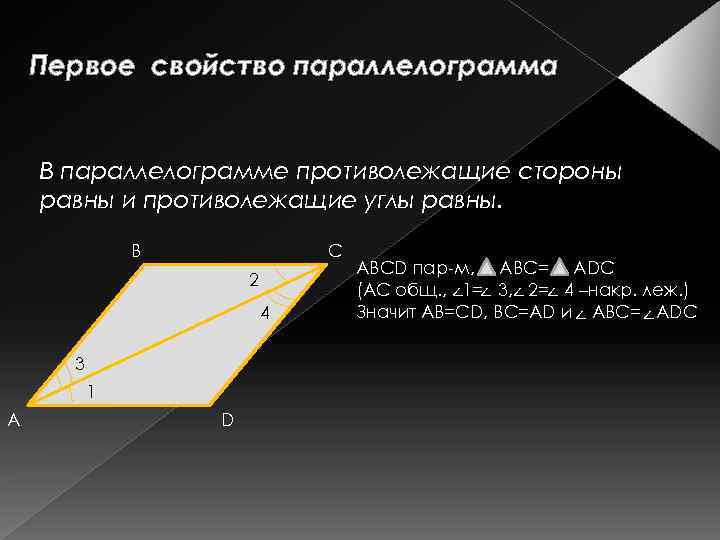Первое свойство параллелограмма В параллелограмме противолежащие стороны равны и противолежащие углы равны. В С 2 4 3 1 А D АВСD пар-м, АВС= АDС (АС общ. , <1=< 3, < 2= < 4 –накр. леж. ) Значит АВ=СD, ВС=АD и < АВС= <АDС

Второе свойство параллелограмма Диагонали параллелограмма точкой пересечения делятся пополам. В С 3 1 0 А 2 4 D Дано: АВСD- пар-м, докажем АО=ОС, ВО=ОD Т. к ВОС= DОА ( <1= <2, < 3= < 4(накр. леж), ВС=АD(Стороны пар-ма).

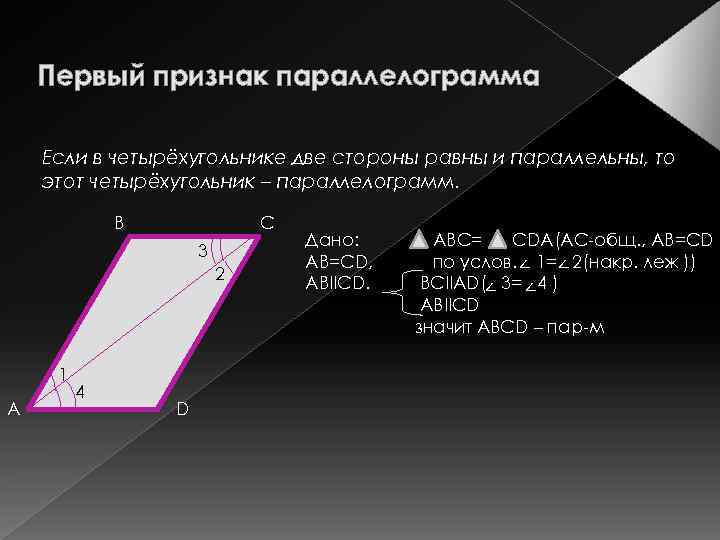Первый признак параллелограмма Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм. В С 3 2 1 А 4 D Дано: АВ=СD, АВIICD. АВС= СDА(АС-общ. , АВ=СD по услов. < 1= < 2(накр. леж )) ВСIIAD( < 3= <4 ) ABIICD значит ABCD – пар-м

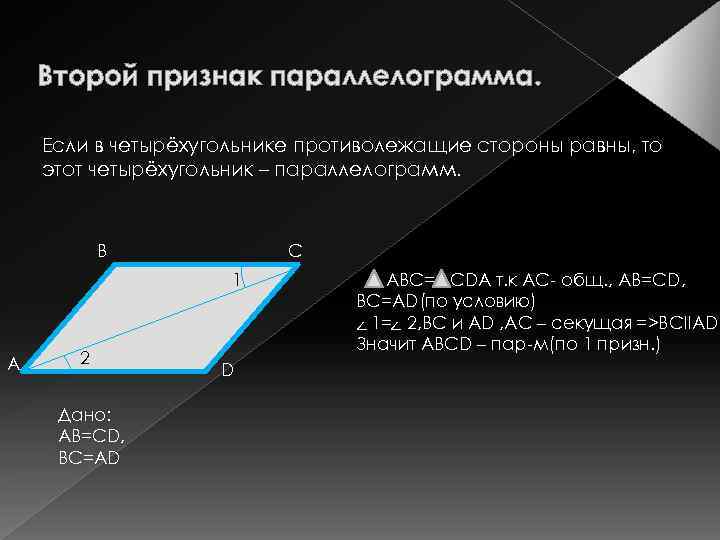Второй признак параллелограмма. Если в четырёхугольнике противолежащие стороны равны, то этот четырёхугольник – параллелограмм. В С 1 А 2 Дано: АВ=СD, ВС=АD D АВС= СDA т. к АС- общ. , АВ=СD, ВС=АD(по условию) < 1= < 2, ВС и AD , AC – секущая =>BCIIAD Значит ABCD – пар-м(по 1 призн. )

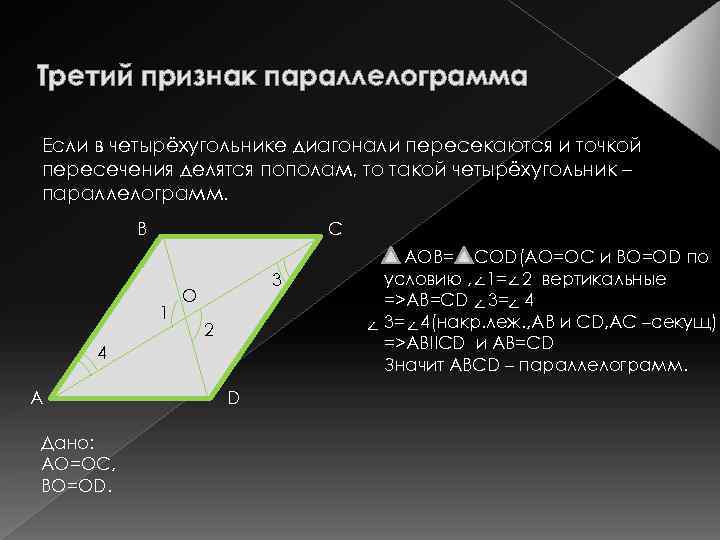Третий признак параллелограмма Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то такой четырёхугольник – параллелограмм. В С 1 3 О 2 4 А Дано: АО=ОС, ВО=ОD. D АОВ= СОD(АО=ОС и ВО=ОD по условию , <1= < 2 вертикальные =>АВ=СD < 3= < 4 < 3= <4(накр. леж. , АВ и СD, AC –секущ) =>ABIICD и AB=CD Значит АВСD – параллелограмм.

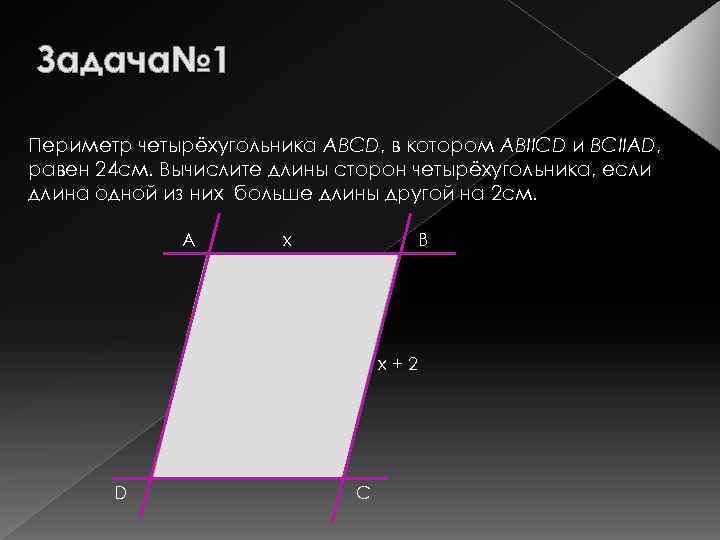Задача№ 1 Периметр четырёхугольника АВCD, в котором АВIICD и BCIIAD, равен 24 см. Вычислите длины сторон четырёхугольника, если длина одной из них больше длины другой на 2 см. А x В x+2 D С

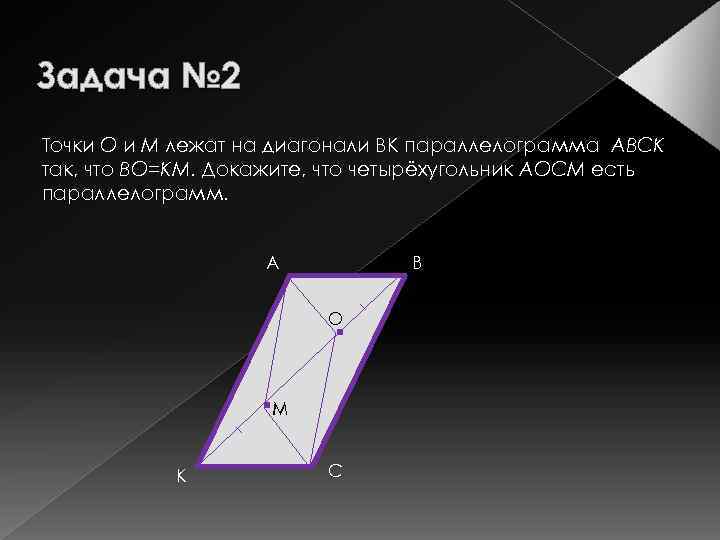Задача № 2 Точки О и М лежат на диагонали ВК параллелограмма АВСК так, что ВО=КМ. Докажите, что четырёхугольник АОСМ есть параллелограмм. А В О М К С

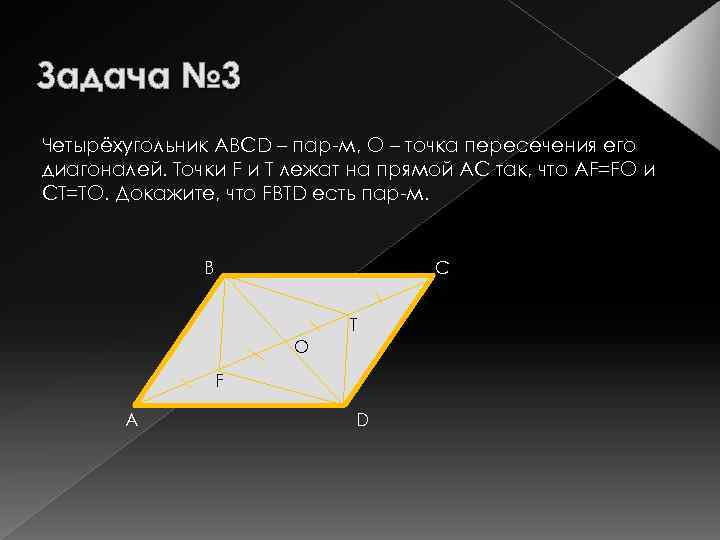Задача № 3 Четырёхугольник АВСD – пар-м, О – точка пересечения его диагоналей. Точки F и Т лежат на прямой АС так, что AF=FO и CT=TO. Докажите, что FBTD есть пар-м. В С Т О F А D