Геометрия древних египтян О зарождении геометрии в

Геометрия древних египтян

О зарождении геометрии в Древнем Египте около 2000 лет до н. э. древнегреческий историк Геродот писал: «Сезострис, египетский фараон, разделил землю, дав каждому египтянину участок по жребию, и взимал соответствующим образом налог с каждого участка. Случалось, что Нил заливал тот или иной участок, тогда пострадавший обращался к царю, а царь посылал землемеров, чтобы установить, на сколько уменьшился участок, и соответствующим образом уменьшить налог. Так возникла геометрия в Египте, а оттуда перешла в Грецию» .

Евдем Родосский (до 350 – после 322 до н. э. ) – древнегреческий философ, ученик Аристотеля писал: «Геометрия была открыта египтянами и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития р. Нил, постоянно смывавшего границы»

Греческий философ Прокл Византийский отмечал в своем сочинении: «Согласно большинству мнений, геометрия была впервые открыта в Египте, имела свое происхождение в измерении площадей»

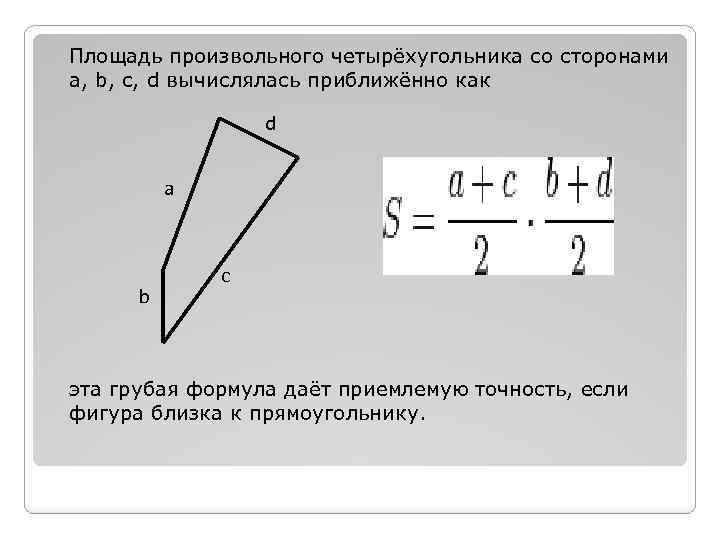Площадь произвольного четырёхугольника со сторонами a, b, c, d вычислялась приближённо как d a b c эта грубая формула даёт приемлемую точность, если фигура близка к прямоугольнику.

Площадь любого параллелограмма со сторонами а и в по этой получается равной S=ab, что может дать достаточно большую ошибку. b h a b a Sпарал-ма=a*h

Надписи на стенах храма в г. Эдфу “ 22 на 25, 4 на 4, это равно 90; ничего на 5, 17 на 7, это равно 42 12. ” Результаты вычисляются так: ((22+23)2)*((4+4)2=90; ((0+5)2)*((17+17)2)=42 12

Первая фигура не является прямоугольником. Площадь треугольника согласно второй надписи вычисляется так: S=(c2)*(b+d)2 h

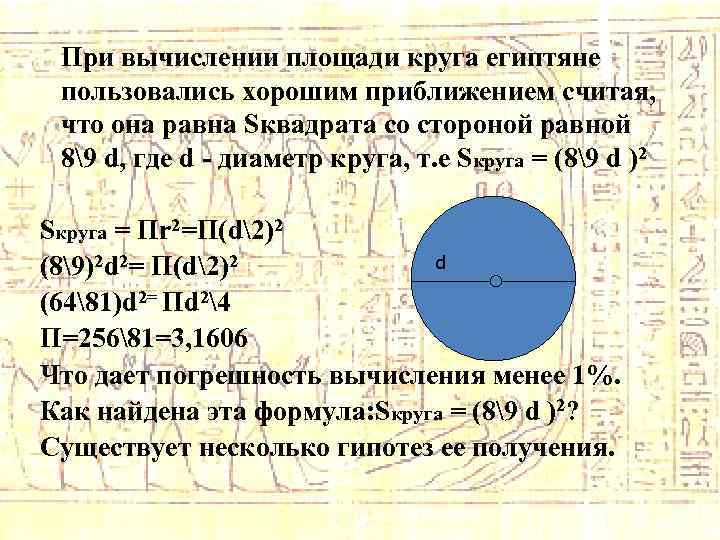При вычислении площади круга египтяне пользовались хорошим приближением считая, что она равна Sквадрата со стороной равной 89 d, где d - диаметр круга, т. е Sкруга = (89 d )2 Sкруга = Пr 2=П(d2)2 d (89)2 d 2= П(d2)2 (6481)d 2= Пd 24 П=25681=3, 1606 Что дает погрешность вычисления менее 1%. Как найдена эта формула: Sкруга = (89 d )2? Существует несколько гипотез ее получения.

Рассмотрим задачу R 48. Sф=d 2 -4*(12)*(d3)2= =d 2 -(29)*d 2=(79)*d 2 d3 79=(7*9)(9*9)= =(8*8)(9*9)=(89)2 Sф Первый способ d

Второй способ Принадлежит профессору А. Е. Райк. Удалялось 4 квадрата со стороной (16)d и 8 квадратов со сторонами (19)d. S=d 2 -4*((16)*d)2 -8*((19)*d)2 =d 2 -(19)*d 2 -(881)*d 2= =d 2(1 -19)-(19)*(1 -19)*d 2= =(1 -19)*d 2= =(89)*d 2=((89)*d)2 Эта гипотеза хорошо согласуется с задачей М 10 из московского папируса.

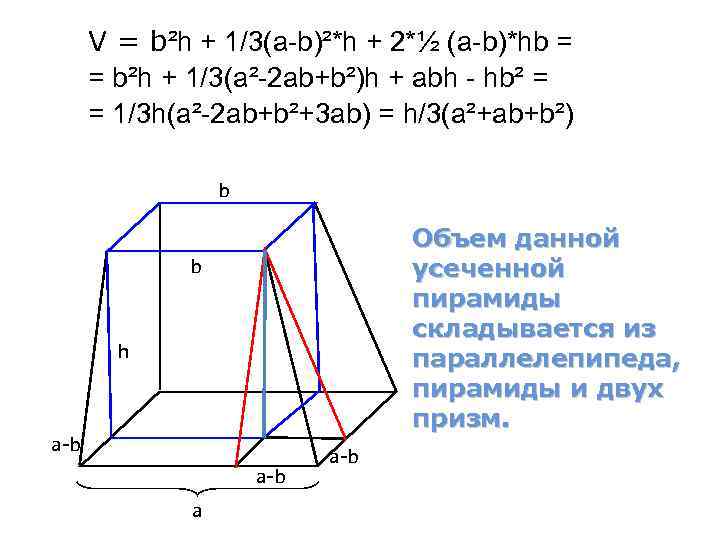V = b²h + 1/3(a-b)²*h + 2*½ (a-b)*hb = = b²h + 1/3(a²-2 ab+b²)h + abh - hb² = = 1/3 h(a²-2 ab+b²+3 ab) = h/3(a²+ab+b²) b Объем данной усеченной пирамиды складывается из параллелепипеда, пирамиды и двух призм. b h a-b a a-b

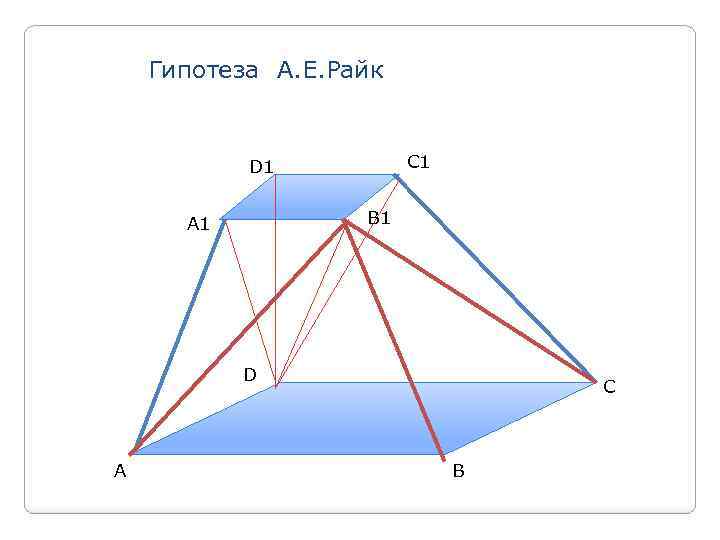Гипотеза А. Е. Райк C 1 D 1 B 1 A 1 D A C B