Геометрия Что изучает геометрия Слово геометрия

Геометрия

Что изучает геометрия? Слово «геометрия» – греческое , оно составлено из двух частей «гео» и «метрия» и дословно на русский язык переводится как «земле-мерие» .

Разделы геометрии Современная геометрия включает в себя следующие дополнительные разделы: Многомерная геометрия. Неевклидовы геометрии. Сферическая геометрия. Геометрия Лобачевского. Риманова геометрия. Геометрия многообразий.

«Геометрия» – это раздел математики, изучающий пространственные формы и их отношения» . «Геометрия – это наука о свойствах геометрических фигур» .

При изучении геометрии нас интересуют геометрические форма и размеры тела. Например, и деревянный, и картонный куб носят одно и тоже название-куб. Также футбольный мяч, резиновый мяч и мыльный пузырь имеют одну и ту же форму-шар.

Если не обращать внимания на свойства предмета (материал, цвет), а рассматривать только его форму и размеры, то этому предмету можно дать название геометрической фигуры или тела.

Возникновение геометрии О Зарождении геометрии около двух тысяч лет назад древнегреческий ученый Геродот писал: Египетский фараон, разделил землю, дав каждому египтянину участок по жребию и брал налог с каждого участка. Иногда Нил заливал участки земли, и пострадавшие просили землемеров перемерить участки , чтобы уменьшить налоги. Так возникла геометрия в Египте, а оттуда перешла в Грецию.

История возникновения геометрии Уже 200 тысяч лет тому назад были изготовлены орудия сравнительно правильной геометрической формы, а потом люди научились шлифовать их. Специальных названий для геометрических фигур, конечно, не было. Говорили: «такой же, как кокосовый орех» или «такой же, как соль» и т. д. А когда люди стали строить дома из дерева, пришлось глубже разобраться в том, какую форму следует придавать стенам и крыше, какой формы должны быть бревна. Сами того не зная, люди все время занимались геометрией: женщины, изготавливая одежду, охотники, изготавливая наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.

Так практическая деятельность людей привела к дальнейшему углублению знаний о формах фигур, развитию геометрии. Люди стали учиться измерять и площади, и объемы, и длины и т. д. Древние египтяне были замечательными инженерами. До сих пор не могут до конца разгадать загадки огромных гробниц Египетских царей – Фараонов. Пирамиды – а они построены более 5 тыс. лет назад – состоят из каменных блоков весом 15 тонн, и эти «кирпичики» так подогнаны друг к другу, что не возможно между ними протиснуть и почтовую открытку. А при строительстве использовали лишь простейшие механизмы – рычаги и катки.

Почти все великие ученые древности и средних веков были выдающимися геометрами. Девиз древней школы был: "Не знающие геометрии не допускаются!" И наиболее удачно была изложена геометрия, как наука о свойствах геометрических фигур, греческим ученым Евклидом (III в. до н. э. ) в его 13 томах «Начала» . Евклид жил в Александрии, был современником царя Птоломея I и учеником Платона. Величайшая заслуга его состояла в том, что он подвел итог построению геометрии придал ее изложению столь совершенную форму, что на 2 тысячи лет «Начала» стали основным руководством по геометрии.

Конечно, геометрия не может быть создана одним ученым. В работе Евклид опирался на труды десятков предшественников и дополнил работу своими открытиями и изысканиями. Сотни раз книги были переписаны от руки, а когда изобрели книгопечатание, то она много раз переиздавалась на языках всех народов и стала одной из самых распространенных книг в мире. В одной легенде говорится, что однажды египетский царь Птолемей I спросил древнегреческого математика, нет ли более короткого пути для понимания геометрии, чем тот, который описан в его знаменитом труде, содержащемся в 13 книгах. Ученый гордо ответил: " В геометрии нет царской дороги".

Геометрия не только дает представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать, делать выводы, т. е. логически мыслить.

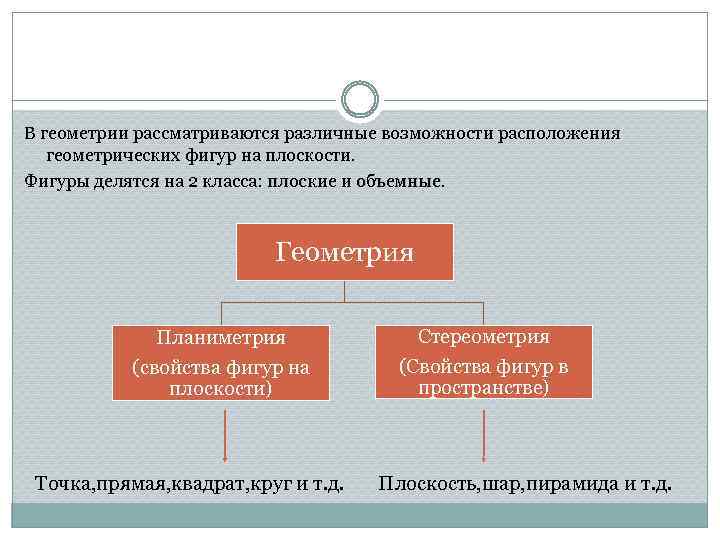В геометрии рассматриваются различные возможности расположения геометрических фигур на плоскости. Фигуры делятся на 2 класса: плоские и объемные. Геометрия Планиметрия (свойства фигур на плоскости) Точка, прямая, квадрат, круг и т. д. Стереометрия (Свойства фигур в пространстве) Плоскость, шар, пирамида и т. д.

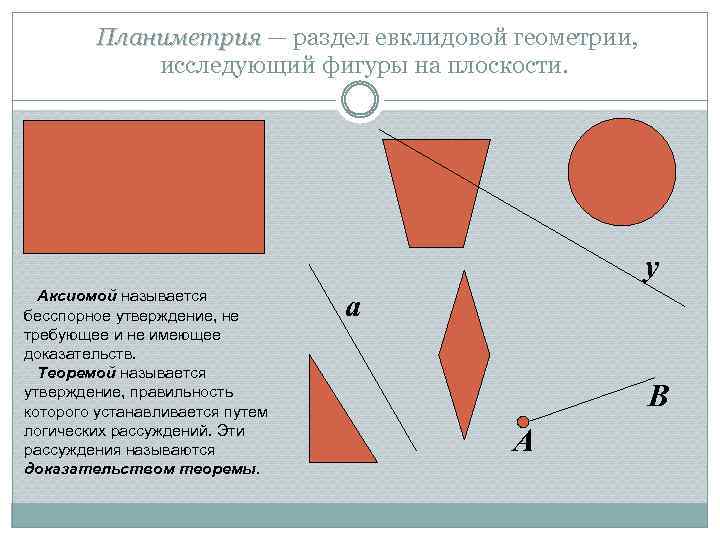Планиметрия — раздел евклидовой геометрии, Планиметрия исследующий фигуры на плоскости. у Аксиомой называется бесспорное утверждение, не требующее и не имеющее доказательств. Теоремой называется утверждение, правильность которого устанавливается путем логических рассуждений. Эти рассуждения называются доказательством теоремы. а В А

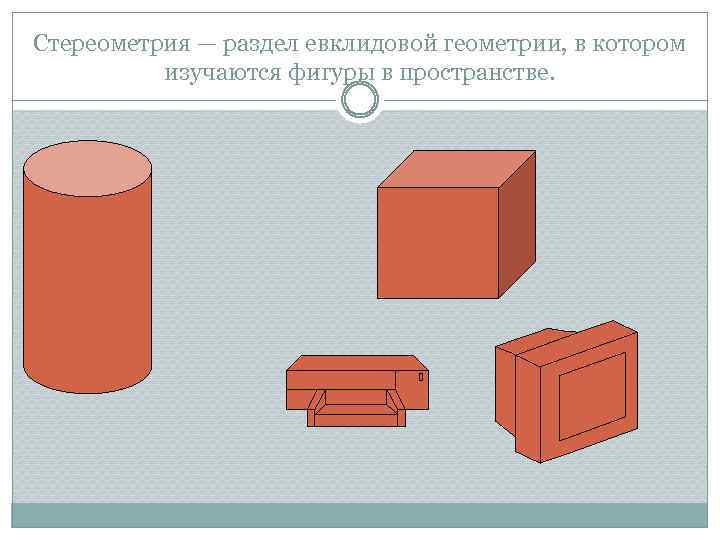Стереометрия — раздел евклидовой геометрии, в котором изучаются фигуры в пространстве.

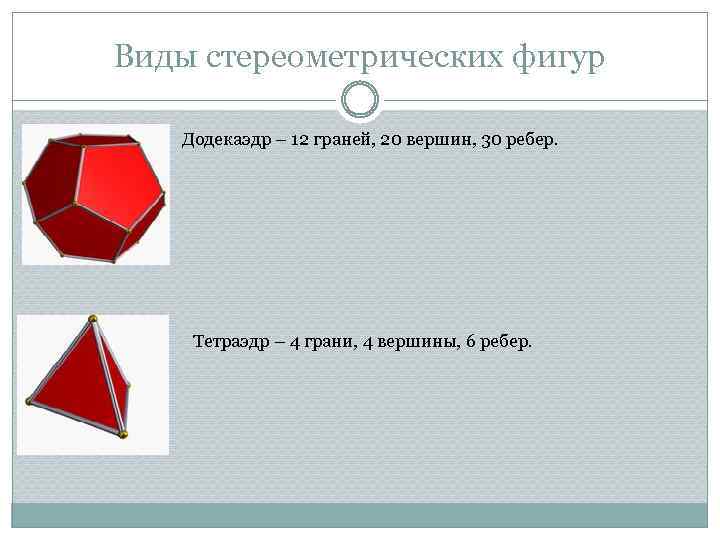Виды стереометрических фигур Додекаэдр – 12 граней, 20 вершин, 30 ребер. Тетраэдр – 4 грани, 4 вершины, 6 ребер.

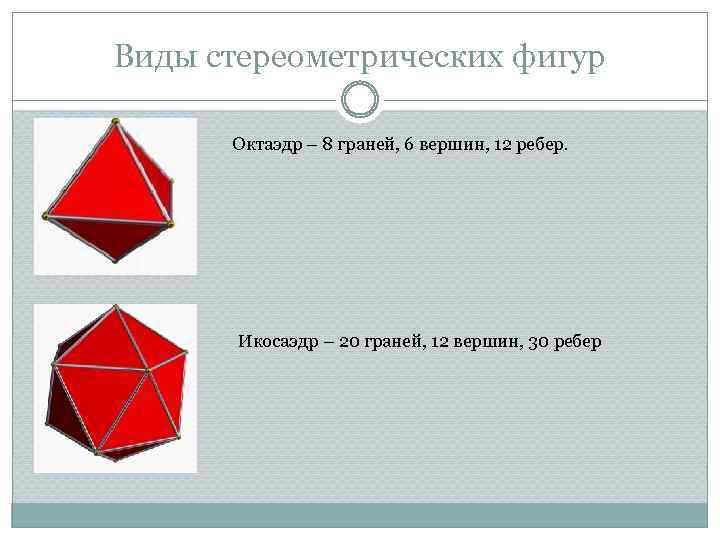Виды стереометрических фигур Октаэдр – 8 граней, 6 вершин, 12 ребер. Икосаэдр – 20 граней, 12 вершин, 30 ребер

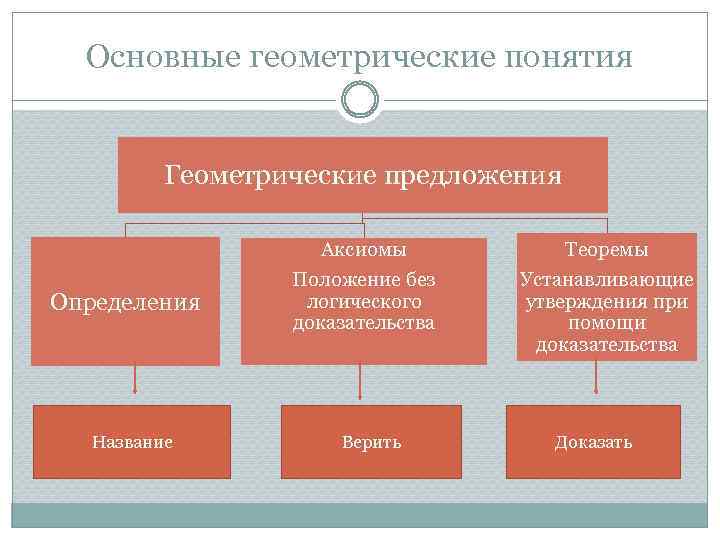Основные геометрические понятия Геометрические предложения Определения Название Аксиомы Положение без логического доказательства Верить Теоремы Устанавливающие утверждения при помощи доказательства Доказать

классической геометрии можно выделить следующие основные разделы: Евклидова геометрия, в которой предполагается, что размеры отрезков и углов при перемещении фигур на плоскости не меняются. Другими словами, это теория тех свойств фигур, которые сохраняются при их переносе, вращении и отражении. Планиметрия — раздел евклидовой геометрии, исследующий фигуры на плоскости. Стереометрия — раздел евклидовой геометрии, в котором изучаются фигуры в пространстве. Проективная геометрия, изучающую проективные свойства фигур, то есть свойства, сохраняющиеся при их проективных преобразованиях. Инварианты в этой геометрии — это свойства, сохраняющиеся при замене фигур на подобные им, но другого размера. Аффинная геометрия, использующая очень общие аффинные преобразования. В ней длины и величины углов не имеют существенного значения, но прямые переходят в прямые. Начертательная геометрия — инженерная дисциплина, в основе которой лежит метод проекций. Этот метод использует две и более проекций (ортогональных или косоугольных), что позволяет представить трехмерный объект на плоскости.

Литература Каган В. Ф. Очерки по геометрии. -М. : Московский университет, 1963. Свечников А. А. Путешествия в историю математике или как люди научились считать. М. : Просвещение, 1995.

Презентацию выполнили: Ученики МБОУ гимназии № 1 7 -2 класса Момот Полина Игнатьева Анна Кичатов Игорь Рыкова Анна Мещеряков Влад Юшков Никита