Геометрия 9 класс Тема «Движения»








 Геометрия 9 класс Тема «Движения» Выполнила Котомина О. В. учитель математики высшей категории ГБОУ СОШ № 51
Геометрия 9 класс Тема «Движения» Выполнила Котомина О. В. учитель математики высшей категории ГБОУ СОШ № 51
 Содержание Определение Виды движения Свойства движения Задачи на построение Примеры движения в курсе алгебры Движение вокруг нас
Содержание Определение Виды движения Свойства движения Задачи на построение Примеры движения в курсе алгебры Движение вокруг нас
 Любое отображение, при котором сохраняется расстояние между точками , называется ДВИЖЕНИЕМ.
Любое отображение, при котором сохраняется расстояние между точками , называется ДВИЖЕНИЕМ.
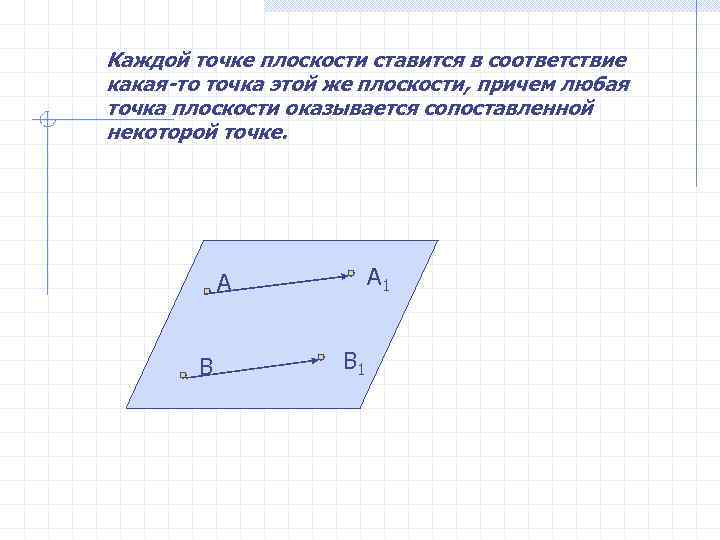
 Каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. А А 1 В В 1
Каждой точке плоскости ставится в соответствие какая-то точка этой же плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. А А 1 В В 1
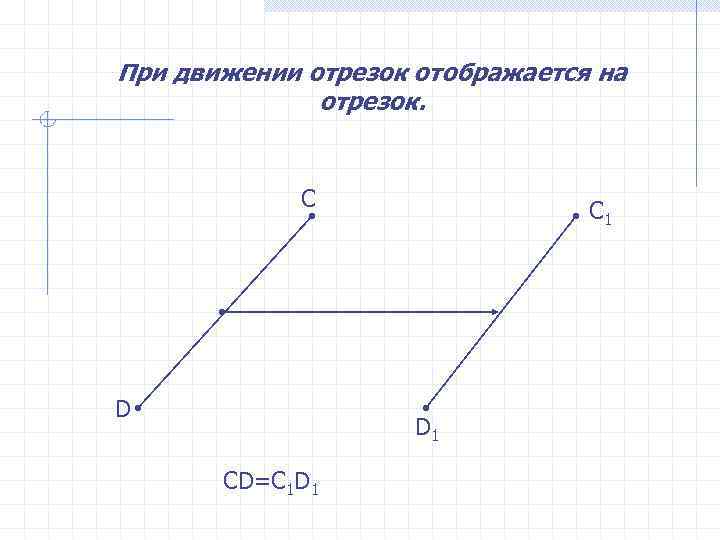
 При движении отрезок отображается на отрезок. С C 1 D D 1 CD=C 1 D 1
При движении отрезок отображается на отрезок. С C 1 D D 1 CD=C 1 D 1
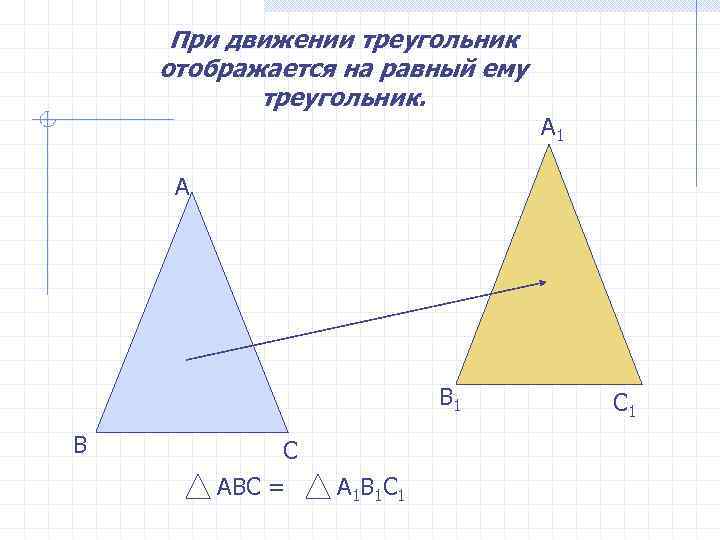
 При движении треугольник отображается на равный ему треугольник. А 1 А В 1 С 1 В С АВС = А 1 В 1 С 1
При движении треугольник отображается на равный ему треугольник. А 1 А В 1 С 1 В С АВС = А 1 В 1 С 1
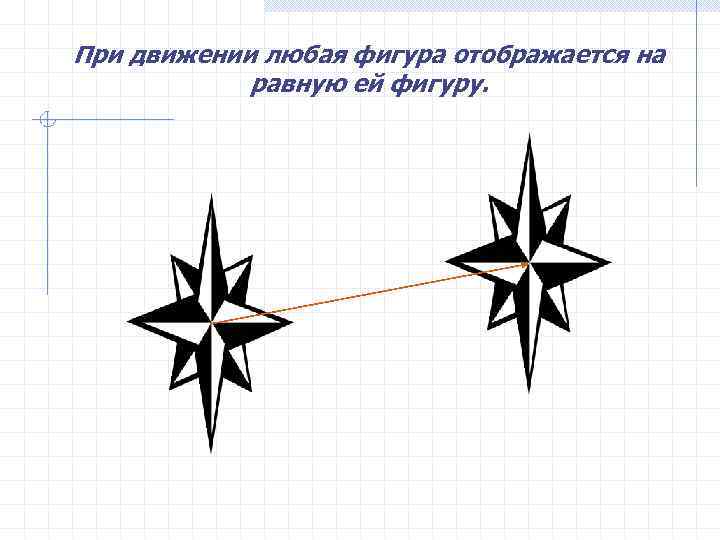
 При движении любая фигура отображается на равную ей фигуру.
При движении любая фигура отображается на равную ей фигуру.
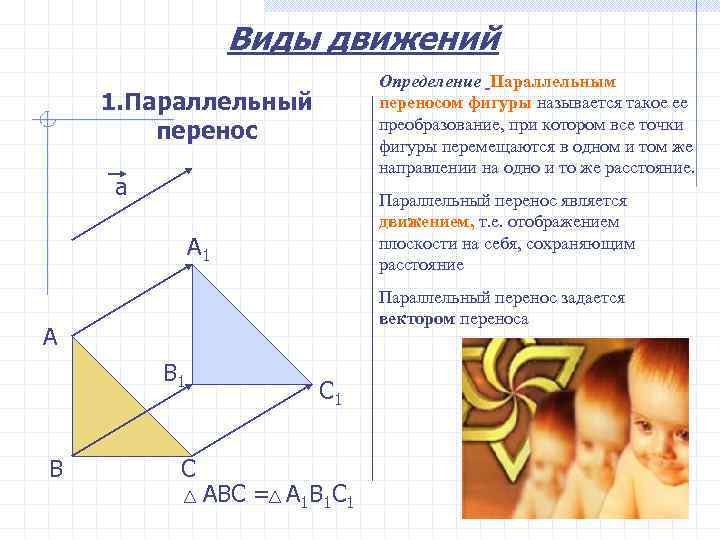
 Виды движений Определение Параллельным 1. Параллельный переносом фигуры называется такое ее преобразование, при котором все точки перенос фигуры перемещаются в одном и том же направлении на одно и то же расстояние. а Параллельный перенос является движением, т. е. отображением A 1 плоскости на себя, сохраняющим расстояние Параллельный перенос задается вектором переноса A B 1 C 1 B C АВС = А 1 В 1 С 1
Виды движений Определение Параллельным 1. Параллельный переносом фигуры называется такое ее преобразование, при котором все точки перенос фигуры перемещаются в одном и том же направлении на одно и то же расстояние. а Параллельный перенос является движением, т. е. отображением A 1 плоскости на себя, сохраняющим расстояние Параллельный перенос задается вектором переноса A B 1 C 1 B C АВС = А 1 В 1 С 1
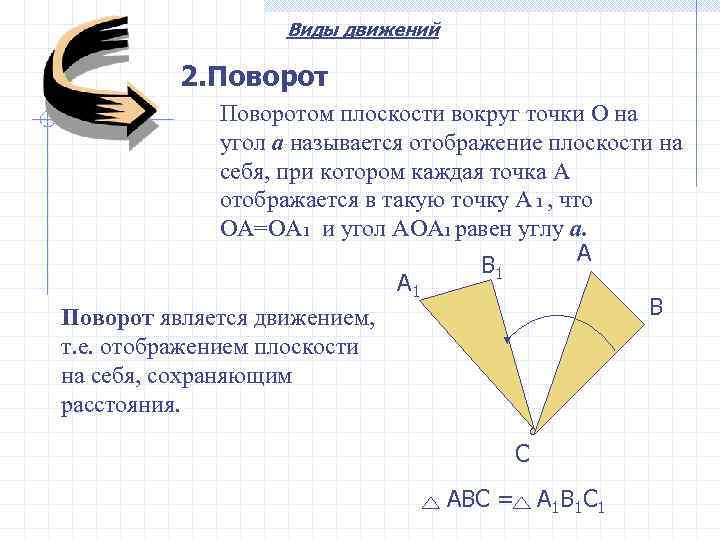
 Виды движений 2. Поворот Поворотом плоскости вокруг точки О на угол a называется отображение плоскости на себя, при котором каждая точка А отображается в такую точку А 1 , что ОА=ОА 1 и угол АОА 1 равен углу a. A B 1 A 1 Поворот является движением, B т. е. отображением плоскости на себя, сохраняющим расстояния. C АВС = А 1 В 1 С 1
Виды движений 2. Поворот Поворотом плоскости вокруг точки О на угол a называется отображение плоскости на себя, при котором каждая точка А отображается в такую точку А 1 , что ОА=ОА 1 и угол АОА 1 равен углу a. A B 1 A 1 Поворот является движением, B т. е. отображением плоскости на себя, сохраняющим расстояния. C АВС = А 1 В 1 С 1
 Особый случай представляет поворот на 180 градусов. Пусть т. О – центр поворота. Чтобы построить точку Х 1 соответствующую точке X, достаточно продолжить отрезок О XО за точку О на отрезок ОХ 1 = ОX. Точки Х 1 и X называются Х симметричными относительно точки О. Точка О - есть центр симметрии.
Особый случай представляет поворот на 180 градусов. Пусть т. О – центр поворота. Чтобы построить точку Х 1 соответствующую точке X, достаточно продолжить отрезок О XО за точку О на отрезок ОХ 1 = ОX. Точки Х 1 и X называются Х симметричными относительно точки О. Точка О - есть центр симметрии.
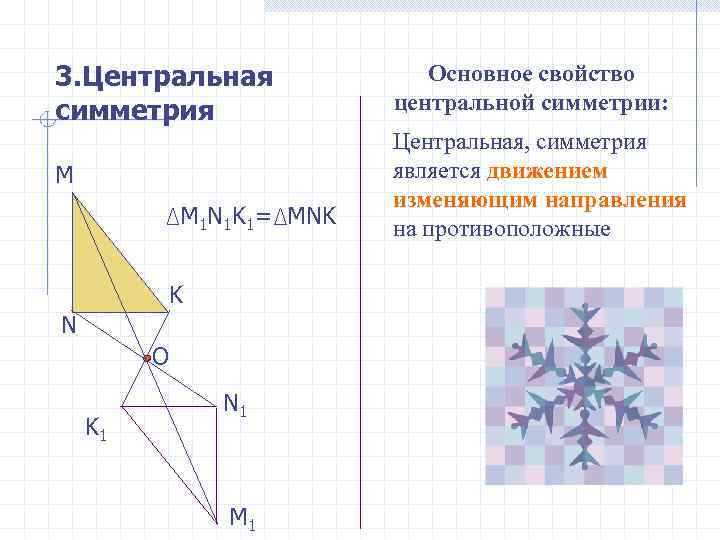
 3. Центральная Основное свойство симметрия центральной симметрии: Центральная, симметрия М является движением изменяющим направления M 1 N 1 K 1= MNK на противоположные K N O N 1 K 1 М 1
3. Центральная Основное свойство симметрия центральной симметрии: Центральная, симметрия М является движением изменяющим направления M 1 N 1 K 1= MNK на противоположные K N O N 1 K 1 М 1
 4. Осевая симметрия Фигура F , полученная отражением фигуры F относительно прямой n, P 1 Q 1 S 1= PQS называется симметричной фигуре F относительно прямой n. P P 1 Точки P 1 называются симметричными относительно прямой n. Прямая n серединный перпендикуляр отрезка PP 1. . Осевая симметрия обладает Q 1 следующим свойством – это отображение плоскости на себя, S 1 которое сохраняет расстояние между точками. n
4. Осевая симметрия Фигура F , полученная отражением фигуры F относительно прямой n, P 1 Q 1 S 1= PQS называется симметричной фигуре F относительно прямой n. P P 1 Точки P 1 называются симметричными относительно прямой n. Прямая n серединный перпендикуляр отрезка PP 1. . Осевая симметрия обладает Q 1 следующим свойством – это отображение плоскости на себя, S 1 которое сохраняет расстояние между точками. n
 Знаете ли вы, что… Слово симметрия означает «соразмерность» . Под симметрией в широком смысле этого слова понимают всякую правильность во внутреннем строении тела или фигуры. Учение о различных видах симметрии представляет большую и важную ветвь геометрии, тесно связанную со многими отраслями естествознания и техники, начиная с текстильного производства (разрисовка тканей) и архитектурной мозаики, а кончая тонкими вопросами строения вещества.
Знаете ли вы, что… Слово симметрия означает «соразмерность» . Под симметрией в широком смысле этого слова понимают всякую правильность во внутреннем строении тела или фигуры. Учение о различных видах симметрии представляет большую и важную ветвь геометрии, тесно связанную со многими отраслями естествознания и техники, начиная с текстильного производства (разрисовка тканей) и архитектурной мозаики, а кончая тонкими вопросами строения вещества.
 Симметрия нас окружает всюду и в природе, и в архитектуре зданий, и в технике, и…
Симметрия нас окружает всюду и в природе, и в архитектуре зданий, и в технике, и…
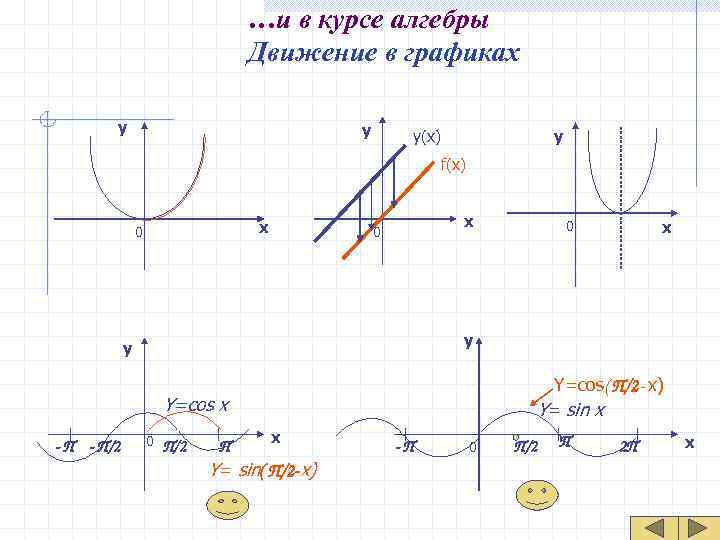
 …и в курсе алгебры Движение в графиках у y(x) у f(x) х 0 у Y=cos( П/2 - x) Y=cos x Y= sin x 0 П/2 х П х - П/2 П -П 0 П/2 2 П Y= sin( П/2 -x)
…и в курсе алгебры Движение в графиках у y(x) у f(x) х 0 у Y=cos( П/2 - x) Y=cos x Y= sin x 0 П/2 х П х - П/2 П -П 0 П/2 2 П Y= sin( П/2 -x)
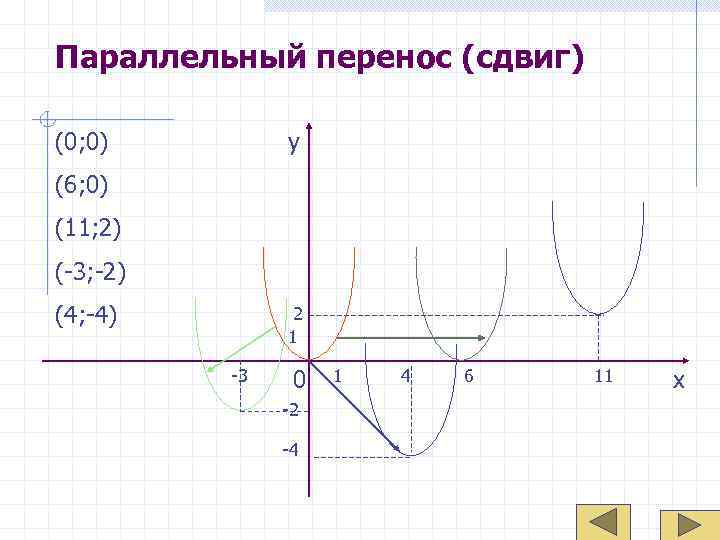
 Параллельный перенос (сдвиг) (0; 0) y (6; 0) (11; 2) (-3; -2) (4; -4) 2 1 -3 0 1 4 6 11 x -2 -4
Параллельный перенос (сдвиг) (0; 0) y (6; 0) (11; 2) (-3; -2) (4; -4) 2 1 -3 0 1 4 6 11 x -2 -4
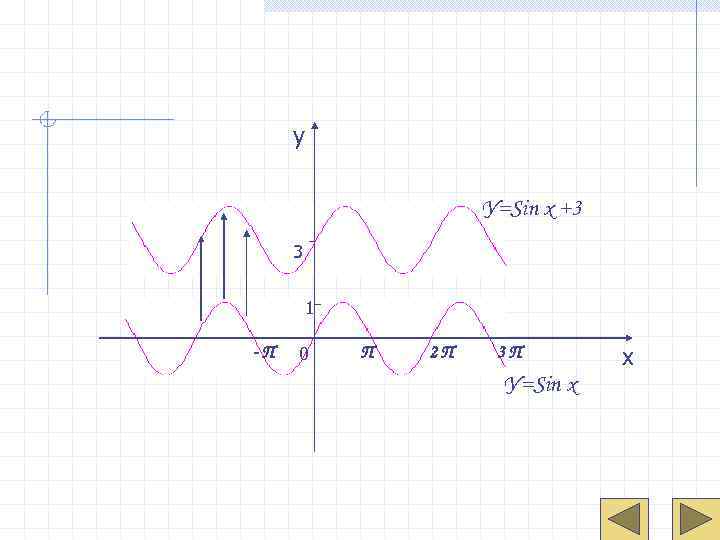
 у У=Sin x +3 3 1 -П 0 П 2 П 3 П х У=Sin x
у У=Sin x +3 3 1 -П 0 П 2 П 3 П х У=Sin x
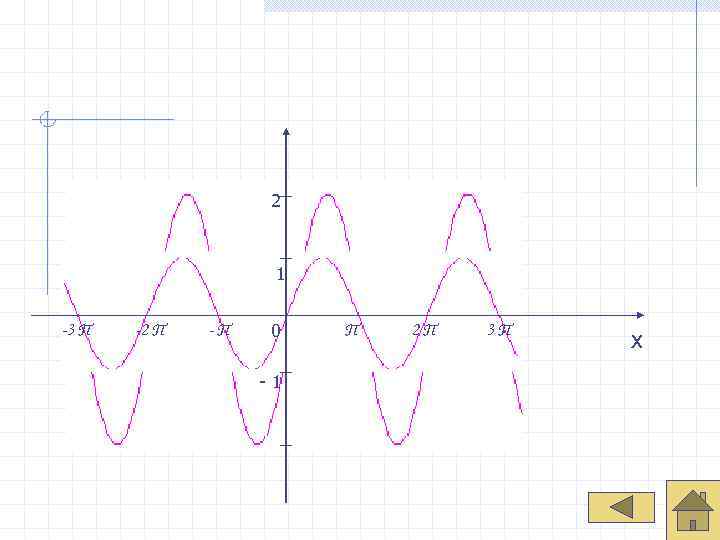
 2 1 -3 П -2 П -П 0 П 2 П 3 П х -1
2 1 -3 П -2 П -П 0 П 2 П 3 П х -1

