Геометрия 8 класс Р О Калошина ГОУ лицей

Геометрия 8 класс Р. О. Калошина, ГОУ лицей № 533

В геометрии специально выделяют задачи на построение, которые решаются только с помощью двух инструментов: ЦИРКУЛЯ И ЛИНЕЙКИ без масштабных делений.

Основные этапы решения задач на построение 1 АНАЛИЗ 2. ПОСТРОЕНИЕ 3. ДОКАЗАТЕЛЬСТВО 4. ИССЛЕДОВАНИЕ В том случае, когда при построении получаются равные фигуры, будем считать, что задача имеет единственное решение.

Задачи 1. 2. 3. 4. 5. Провести в треугольнике высоту из заданной вершины Разделить отрезок на три равные части Разделить отрезок на три части, пропорциональные трем другим отрезкам Даны отрезки a, b, c. Построить отрезок x a, b, c такой, что a: b = c: x В треугольнике провести медиану из заданной вершины

Задача 1. Провести в треугольнике высоту из заданной вершины Чтобы провести высоту в ABC из заданной вершины B, выполните последовательно следующие шаги. ШАГ 1: Установите раствор циркуля больше, чем расстояние от точки B до стороны AC, и проведите две дуги с центрами в точке B, пересекающие AC в точках P и Q. ШАГ 2: Произвольным раствором циркуля проведите две дуги с центрами в точках P и Q. E - точка пересечения этих дуг.

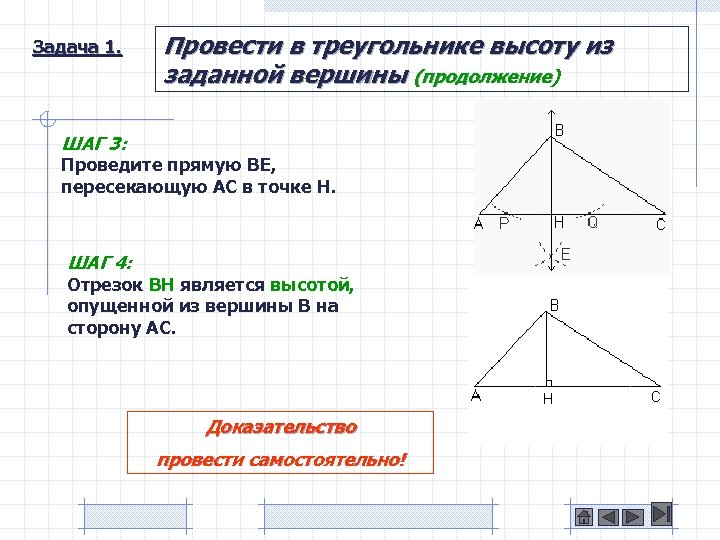Задача 1. Провести в треугольнике высоту из заданной вершины (продолжение) ШАГ 3: Проведите прямую BE, пересекающую AC в точке H. ШАГ 4: Отрезок BH является высотой, опущенной из вершины B на сторону AC. Доказательство провести самостоятельно!

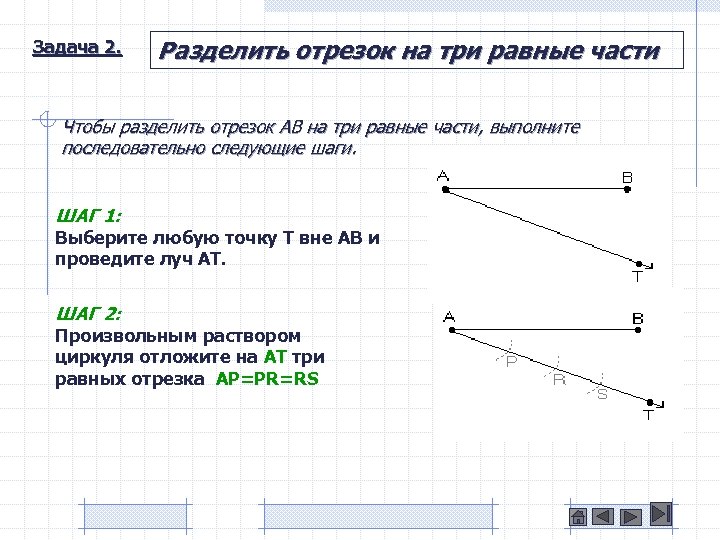Задача 2. Разделить отрезок на три равные части Чтобы разделить отрезок AB на три равные части, выполните последовательно следующие шаги. ШАГ 1: Выберите любую точку T вне AB и проведите луч AT. ШАГ 2: Произвольным раствором циркуля отложите на AT три равных отрезка AP=PR=RS

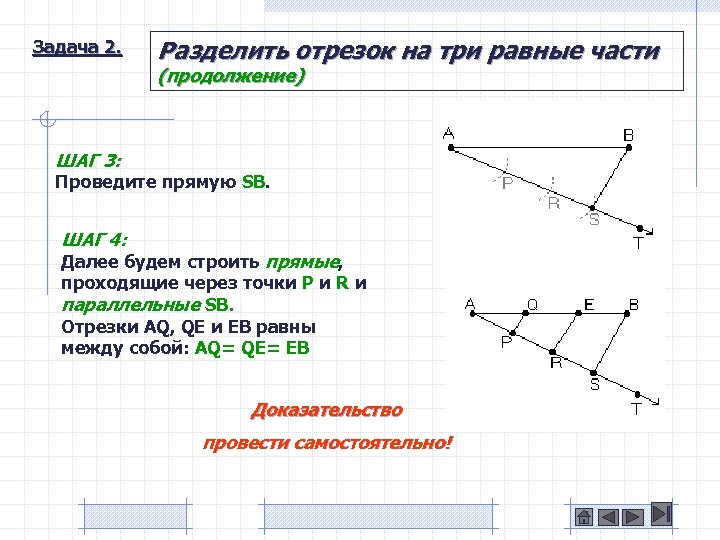Задача 2. Разделить отрезок на три равные части (продолжение) ШАГ 3: Проведите прямую SB. ШАГ 4: Далее будем строить прямые, проходящие через точки P и R и параллельные SB. Отрезки AQ, QE и EB равны между собой: AQ= QE= EB Доказательство провести самостоятельно!

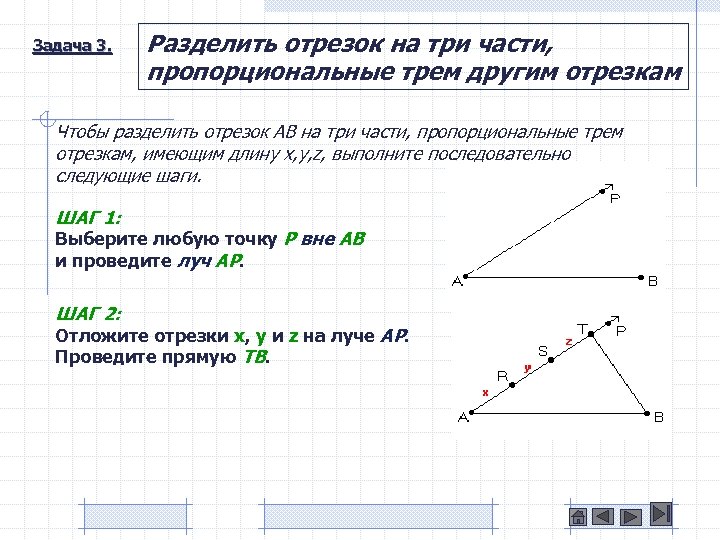Задача 3. Разделить отрезок на три части, пропорциональные трем другим отрезкам Чтобы разделить отрезок AB на три части, пропорциональные трем отрезкам, имеющим длину x, y, z, выполните последовательно следующие шаги. ШАГ 1: Выберите любую точку P вне AB и проведите луч AP. ШАГ 2: Отложите отрезки x, y и z на луче AP. Проведите прямую TB.

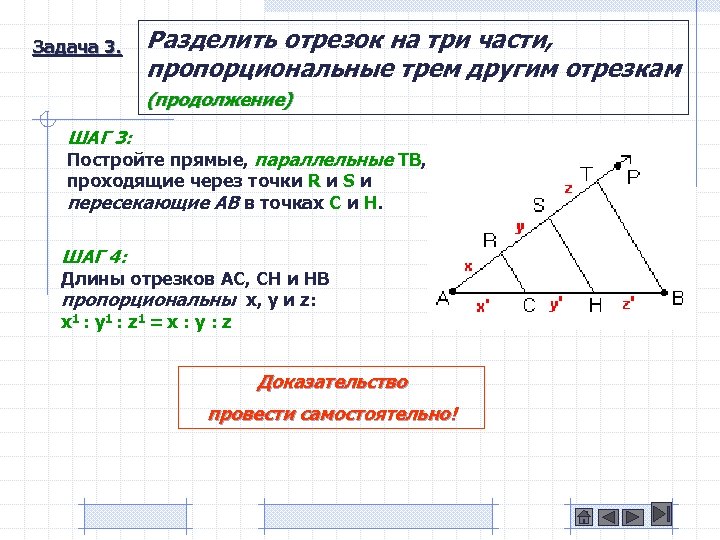Задача 3. Разделить отрезок на три части, пропорциональные трем другим отрезкам (продолжение) ШАГ 3: Постройте прямые, параллельные TB, проходящие через точки R и S и пересекающие AB в точках C и H. ШАГ 4: Длины отрезков AC, CH и HB пропорциональны x, y и z: x 1 : y 1 : z 1 = x : y : z Доказательство провести самостоятельно!

Задача 4. Даны отрезки a, b, c. Построить отрезок x a, b, c такой, что a: b = c: x Чтобы построить отрезок x такой, что a: b = c: x, где a, b, c - данные отрезки, выполните последовательно следующие шаги. отрезки ШАГ 1: Начертите произвольный острый ABC. ШАГ 2: Отложите циркулем отрезки BR=a и RS=b на луче BC и отрезок BT=c на луче BA.

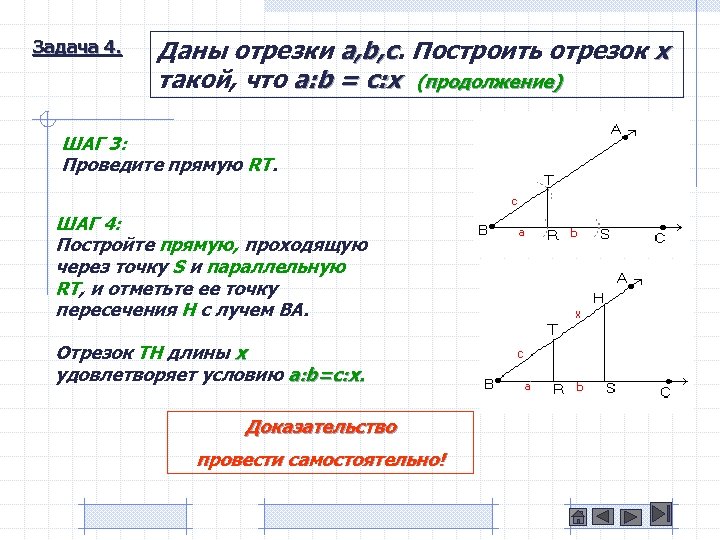Задача 4. Даны отрезки a, b, c. Построить отрезок x a, b, c такой, что a: b = c: x (продолжение) ШАГ 3: Проведите прямую RT. ШАГ 4: Постройте прямую, проходящую через точку S и параллельную RT, и отметьте ее точку пересечения H с лучем BA. Отрезок TH длины x удовлетворяет условию a: b=c: x. Доказательство провести самостоятельно!

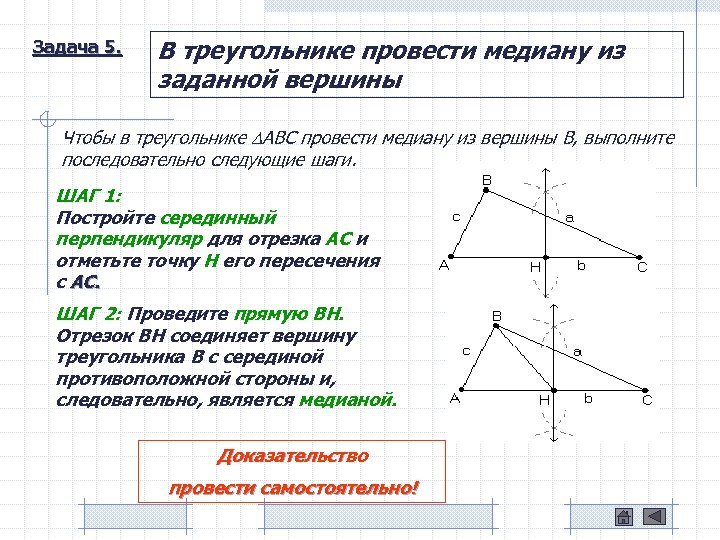Задача 5. В треугольнике провести медиану из заданной вершины Чтобы в треугольнике ABC провести медиану из вершины B, выполните последовательно следующие шаги. ШАГ 1: Постройте серединный перпендикуляр для отрезка AC и отметьте точку H его пересечения с AC. ШАГ 2: Проведите прямую BH. Отрезок BH соединяет вершину треугольника B с серединой противоположной стороны и, следовательно, является медианой. Доказательство провести самостоятельно!