Геометрия 10 класс профильный уровень План 1

Геометрия, 10 класс (профильный уровень)

План 1. Введение 2. Исторические сведения 3. Основные понятия, связанные с окружностью. 4. Свойство хорд. 5. Свойства касательных. 6. Свойства углов. 7. Задачи. 8. Вывод. 9. Литература.

Введение На протяжении многих веков человечество не переставало пополнять свои научные знания в той или иной область науки. Геометрия, как наука о фигурах на плоскости и в пространстве, неотъемлемо связана со многими из научных дисциплин. Но есть в школьной геометрии особые темы, которые ждешь с нетерпением, предвкушая встречу с невероятно красивым материалом. К таким темам можно отнести тему «Окружность» . В тоже время она является одной из тем, вызывающих наибольшие трудности при изучении. Впервые с темой углы «Углы и отрезки, связанные с окружностью» вы познакомились в 8 классе. Но там на эту тему отводится мало времени, поэтому невозможно увидеть всю красоту и разнообразие задач. Второе ваше знакомство с этой темой происходит в начале 10 класса. Вы повторите и обобщите материал, изученный в 8 классе, и узнаете много нового, более сложного, но в тоже время и интересного.

Из истории об окружности и ее радиусе Самая простая из кривых линий – окружность. Это одна из древнейших геометрических фигур. Философы древности придавали ей большое значение. Еще вавилоняне и древние индийцы считали самым важным элементом окружности – радиус. Слово это латинское и означает «луч» . В древности не было этого термина. Евклид и другие ученые говорили просто «прямая из центра» . В одной латинской рукописи XI в. , названной «Искусство геометрии» , встречается впервые термин «полудиаметр» .

Из истории об окружности и ее радиусе Термин «радиус» впервые встречается в «Геометрии» французского ученого Рамуса, изданной в 1569 г. , затем у Ф. Виета. Последний писал, что «радиус» – «элегантное слово» , которое знаменитые римские поэты Овидий и Виргилий употребляли в смысле «луч» . Известный римский оратор Цицерон как – то сказал «Шар образован равными радиусами(лучами), выходящими из его центра» . Термин «радиус» становиться общепринятым лишь в конце XVII в. Термин «хорда» (от греческого «хорде» – струна) был введен в современном смысле европейскими учеными XII – XII вв. Теоремы о зависимости между хордами и расстоянием их от центра изложены в III книге «Начал» Евклида.

Из истории о касательных к окружности Определение касательной как прямой, имеющей с окружностью только одну общую точку, встречается впервые в учебнике «Элементы геометрии» французского математика Лежандра(1752 – 1833). В «Началах» Евклида дается следующее определение: прямая касается круга, если она встречает круг, но при продолжении не пересекает его. То, что касательная к окружности перпендикулярна к радиусу, проведенному в точку касания, было известно еще Архиту Тарентскому(430 – 365 гг. до н. э. ) Доказательство того, что отрезки касательных, проведенных к окружности из внешней точки, равны, отсутствует у Евклида и приписывается комментаторами «Начал» Герону Александрийскому. Предложение: центр окружности находиться на биссектрисе угла, образованного касательными из данной точки, содержится в одном из произведений греческого математика III в. Паппа.

Из истории о вписанных углах Изложенное в современных учебниках доказательство того, что вписанный угол измеряется половиной дуги, на которую он опирается, дано в «Началах» Евклида. На это предложение ссылается, однако, еще Гиппократ Хиосский (V в. До н. э. ) в своем труде о «луночках» Тот факт, что опирающийся на диаметр вписанный угол – прямой, был известен вавилонянам еще 4000 лет назад. Первое нго доказательство приписывается Памфилией, римской писательницей времен Нерона, Фалесу Милетскому.

Окружность – геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от некоторой точки этой же плоскости на заданное расстояние Центр – данная точка. Радиус – это любой отрезок, соединяющий центр окружности и точку окружности. Хорда – это отрезок, соединяющий две точки окружности. Диаметр – это хорда проходящая через центр окружности. Дуга – любая из двух частей окружности, на которые ее делят две лежащие на ней точки. .

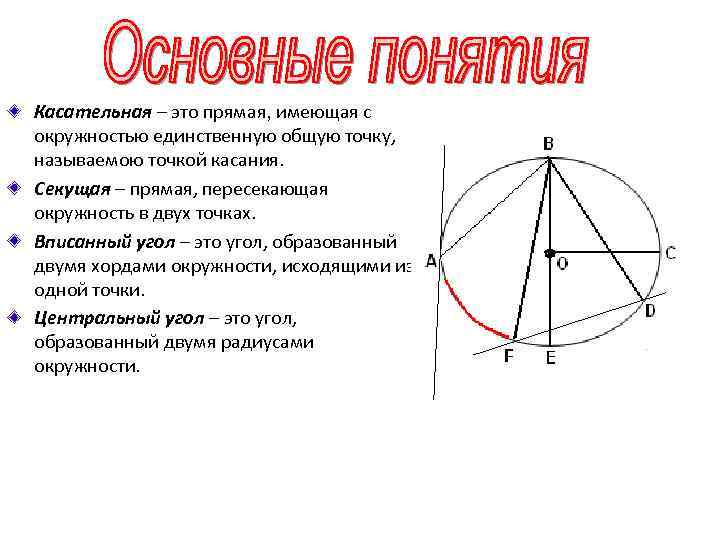Касательная – это прямая, имеющая с окружностью единственную общую точку, называемою точкой касания. Секущая – прямая, пересекающая окружность в двух точках. Вписанный угол – это угол, образованный двумя хордами окружности, исходящими из одной точки. Центральный угол – это угол, образованный двумя радиусами окружности.

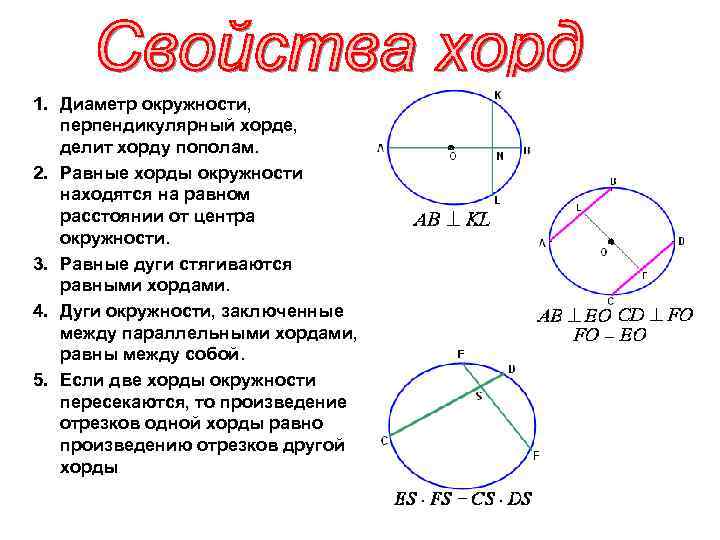1. Диаметр окружности, перпендикулярный хорде, делит хорду пополам. 2. Равные хорды окружности находятся на равном расстоянии от центра окружности. 3. Равные дуги стягиваются равными хордами. 4. Дуги окружности, заключенные между параллельными хордами, равны между собой. 5. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды

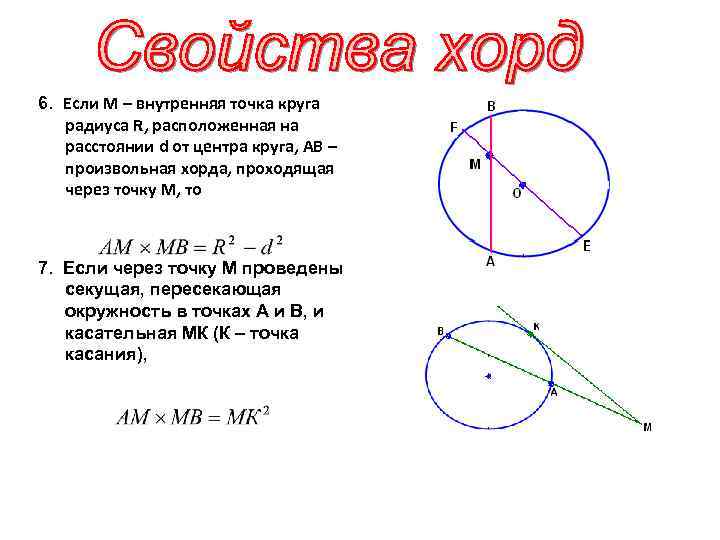6. Если М – внутренняя точка круга радиуса R, расположенная на расстоянии d от центра круга, АВ – произвольная хорда, проходящая через точку М, то 7. Если через точку М проведены секущая, пересекающая окружность в точках А и В, и касательная МК (К – точка касания),

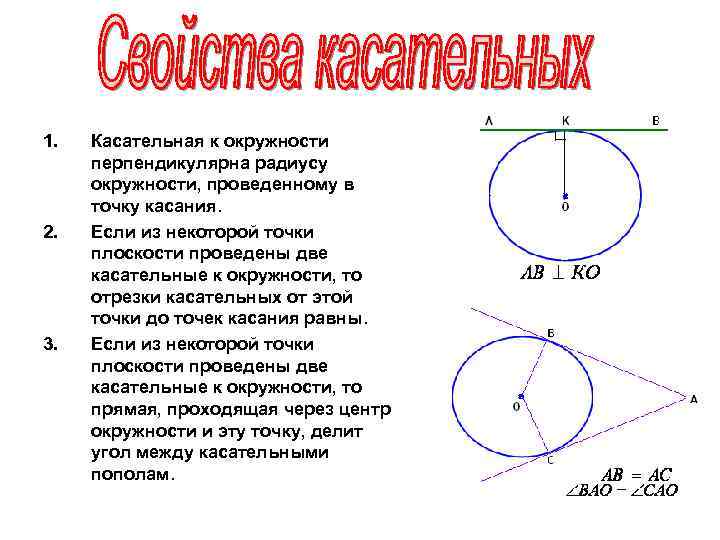1. 2. 3. Касательная к окружности перпендикулярна радиусу окружности, проведенному в точку касания. Если из некоторой точки плоскости проведены две касательные к окружности, то отрезки касательных от этой точки до точек касания равны. Если из некоторой точки плоскости проведены две касательные к окружности, то прямая, проходящая через центр окружности и эту точку, делит угол между касательными пополам.

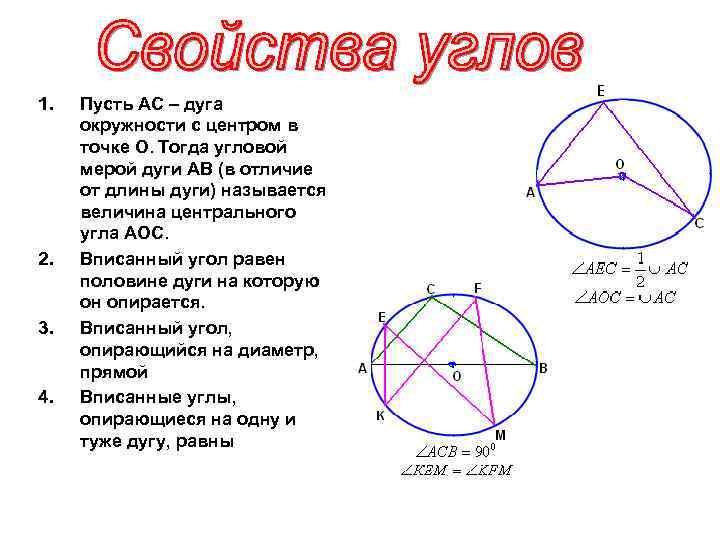1. 2. 3. 4. Пусть АС – дуга окружности с центром в точке О. Тогда угловой мерой дуги АВ (в отличие от длины дуги) называется величина центрального угла АОС. Вписанный угол равен половине дуги на которую он опирается. Вписанный угол, опирающийся на диаметр, прямой Вписанные углы, опирающиеся на одну и туже дугу, равны

1. Угол между двумя пересекающимися хордами измеряется полусуммой заключенных между ними дуг 2. Угол между касательной и хордой, проходящей через точку касания, измеряется половиной заключенной в нем дуги.

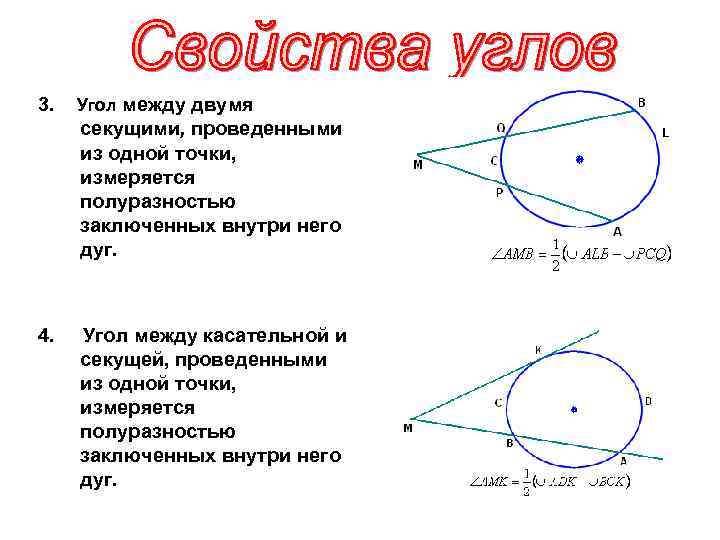3. Угол между двумя секущими, проведенными из одной точки, измеряется полуразностью заключенных внутри него дуг. 4. Угол между касательной и секущей, проведенными из одной точки, измеряется полуразностью заключенных внутри него дуг.

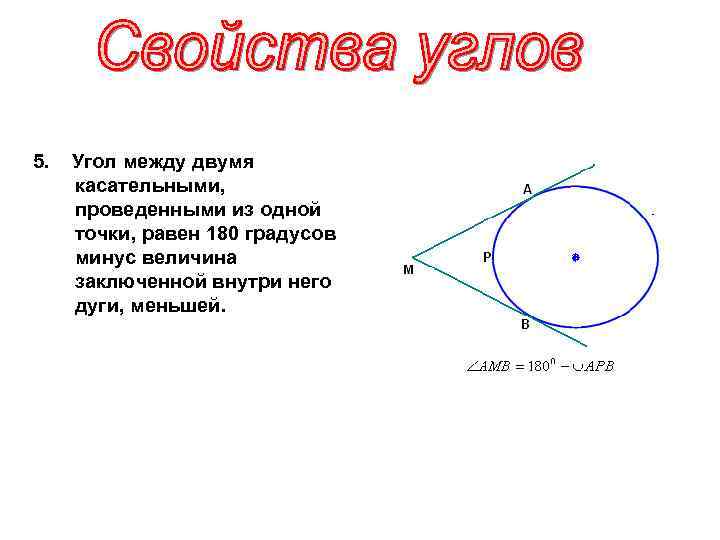5. Угол между двумя касательными, проведенными из одной точки, равен 180 градусов минус величина заключенной внутри него дуги, меньшей.

Литература. 1. Амелькин В. В. , Рабцевич В. Л. , Тимохович В. Л. Геометрия на плоскости: Теория, задачи, решения: учебное пособие по математике. – Мн. : ООО «Асар» , 2003 2. Атанасян Л. С. и др. Геометрия: учебник для 7 – 9 классов общеобразовательных учреждений. – М. : Просвещение, 2003 3. Бахурин Г. А. , Руденко В. Н. Геометрия: учебник для 7 - 9 классов общеобразовательных учреждений. – М: Просвещение, 1994 4. Готман Э. Г. Задачи по планиметрии и методы их решения. – М. : Просвещение, 1996 5. Дополнительные главы к школьному учебнику геометрии 8 класса / Атанасян Л. С. И др. – М. : Просвещение, 1996 6. Кисилев А. П. Элементарная геометрия. – М. : Просвещение, 1996 7. Лоповок Л. М. Тысяча проблемных задач по математике. – М. : Просвещение, 1995 8. Прасолов В. В. Задачи по планиметрии. Часть 2. – М. : Наука. Физматлит, 1995 9. Семенов Е. Е. За страницами учебника геометрии. - 2 -е изд. – М. : Просвещение 1999