Геометрия 10

Геометрия 10 Двугранный угол. Признак перпендикулярности двух плоскостей

Геометрия 10 Двугранный угол. Определение: Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости. Прямая a - ребро, полуплоскости, образующие двугранный угол называют гранями

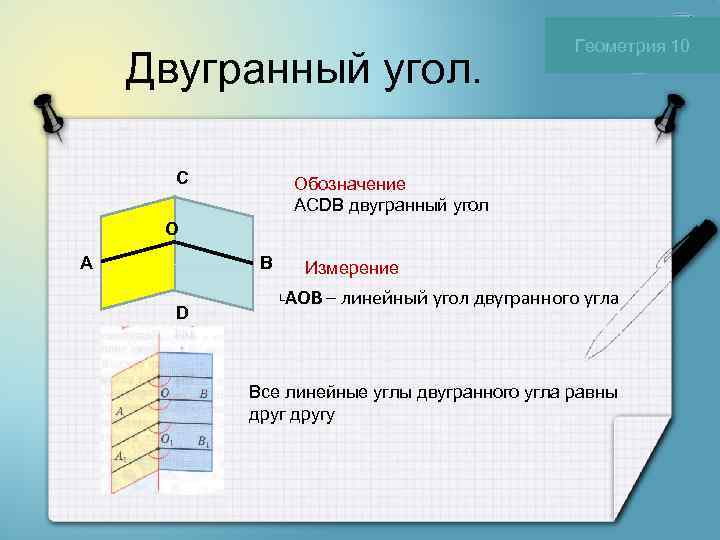Геометрия 10 Двугранный угол. С Обозначение ACDB двугранный угол О A B Измерение AOB – линейный угол двугранного угла └ D Все линейные углы двугранного угла равны другу

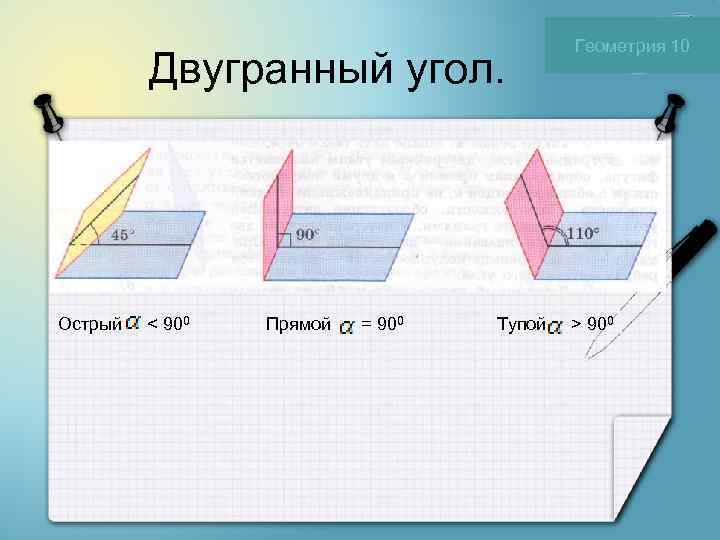Геометрия 10 Двугранный угол. Острый < 900 Прямой = 900 Тупой > 900

Геометрия 10 Признак перпендикулярности двух плоскостей 1. Верно ли, что угол АВС 4. Линейный угол двугранного линейный угол двугранного угла равен 80 0. Найдётся ли угла, если АВ и АС в одной из граней угла перпендикулярны к его прямая перпендикулярная ребру? другой грани? 2. Верно ли, что угол ВАС 5. Угол АВС линейный угол двугранного угла с ребром a , угла, если АВ и АС лежат в Перпендикулярна ли прямая гранях двугранного угла? a плоскости АВС? 3. Верно ли, что угол ВАС линейный угол двугранного 6. Верно ли, что все прямые, угла, если АВ и АС перпендикулярные данной перпендикулярны к его плоскости и пересекающие ребру, а точки В и С лежат данную прямую, лежат в на гранях двугранного угла? одной плоскости?

Признак перпендикулярности двух Геометрия 10 плоскостей Определение: Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 900.

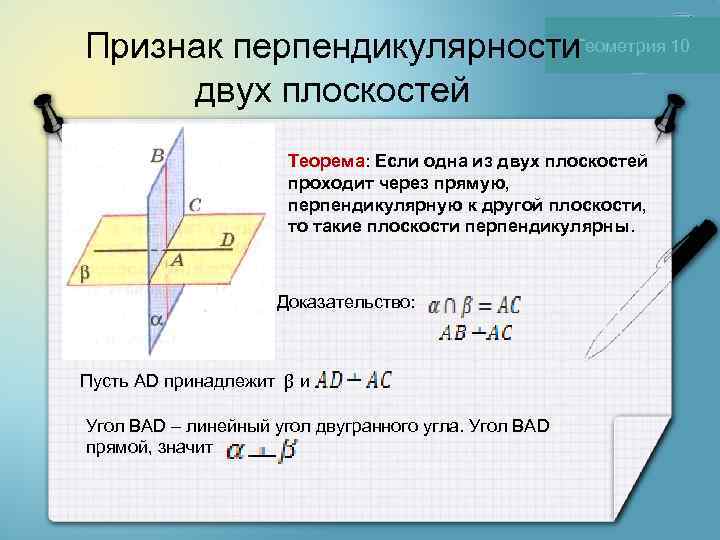Признак перпендикулярности. Геометрия 10 двух плоскостей Теорема: Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны. Доказательство: Пусть АD принадлежит β и Угол ВАD – линейный угол двугранного угла. Угол ВАD прямой, значит

Признак перпендикулярности. Геометрия 10 двух плоскостей При решении задач используют следующие утверждения Следствие : Плоскость, перпендикулярная к ребру двугранного угла, перпендикулярна к его граням. Перпендикуляр, проведённый из любой точки одной из двух взаимно перпендикулярных плоскостей к линии их пересечения, есть перпендикуляр к другой плоскости.

Геометрия 10 Самостоятельно 1. ABCD – тетраэдр, DC=8 см, CB=6 см, AD перпендикулярен плоскости АВС, угол DCB равен 900, угол DBA равен 450. Найдите AD. 2. МABC – тетраэдр, МA перпендикулярен плоскости АВС, МC=4 см, CB =6 см, Угол CAB равен 1200, AC=AB. Найти МA, угол МBC

Геометрия 10 • Домашнее задание: • П. 23 • № 167, 170 – двугранный угол № 173, 174 – перпендикулярность плоскостей П. 24, 25 № 168, 175