Геометрический метод решения задач ЛП Юдина Наталья Алексеевна

Геометрический метод решения задач ЛП Юдина Наталья Алексеевна Курганова Наталья Александровна

Алгоритм решения задачи ЛП • С учетом системы ограничений строим область допустимых решений • Строим вектор С =(с1, с2) – наискорейшего возрастания целевой функции. • Проводим произвольную линию уровня • Определяем оптимальный план и экстремальное значение целевой функции.

Рассмотрим реализацию метода на следующем примере:

Построение области допустимых решений 1. Что на плоскости представляет область допустимых решений? 2. Что на плоскости задает каждое неравенство системы ограничений? • Как построить полуплоскость в заданной системе координат? • Как построить прямую в заданной системе координат?

Построение области допустимых решений • Как построить прямую в заданной системе координат?

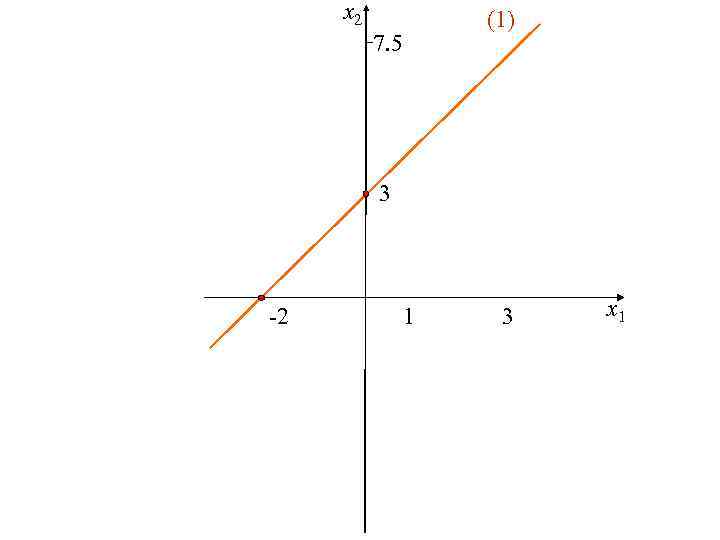
Построение первой прямой (1) 3 х1 – 2 х2 = – 6 Пусть х1= 0, Пусть х2= 0, 3· 0 – 2 х2 = – 6, 3 х1– 2 · 0 = – 6, х2 = 3. х1 = – 2. Координаты первой точки прямой (0; 3) Координаты второй точки прямой (– 2; 0)

x 2 (1) 7. 5 3 -2 1 3 x 1

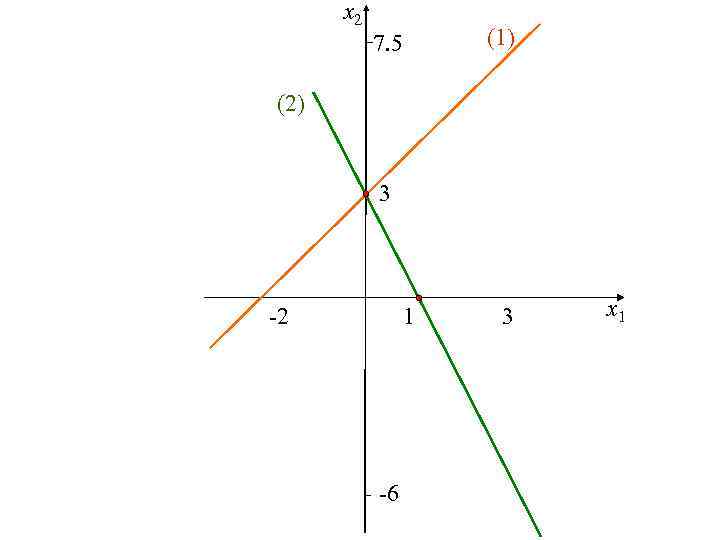
Построение второй прямой (2) 3 х1 + х2 = 3 Пусть х1= 0, Пусть х2= 0, 3· 0 + х2 = 3, 3 х1+ 0 = 3, х2 = 3. х1 = 1. Координаты первой точки прямой (0; 3) Координаты второй точки прямой (1; 0)

x 2 (1) 7. 5 (2) 3 -2 1 -6 3 x 1

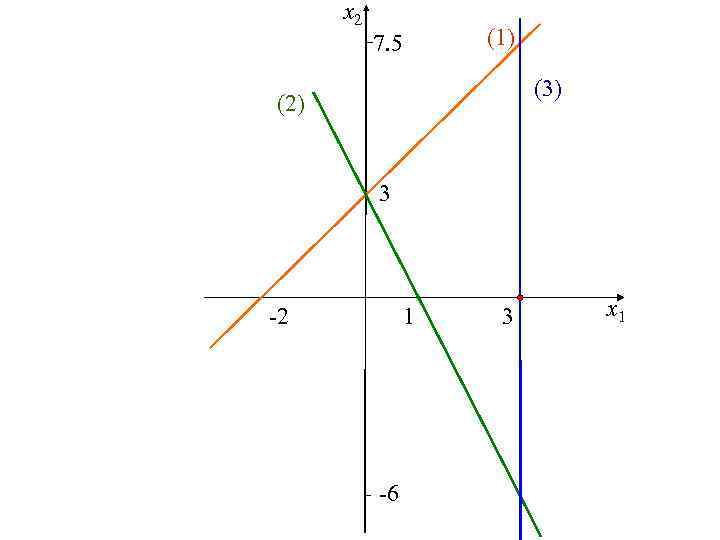
Построение третьей прямой (3) х1= 3 Что представляет собой прямая, выраженная данным уравнением? Прямая, проходящая через точку (3; 0), параллельно координатной оси ОX 2.

x 2 (1) 7. 5 (3) (2) 3 -2 1 -6 3 x 1

Построение области допустимых решений • Как выбрать полуплоскость для каждой прямой в заданной системе координат? • Заменяя каждое ограничение равенствами, построили прямые.

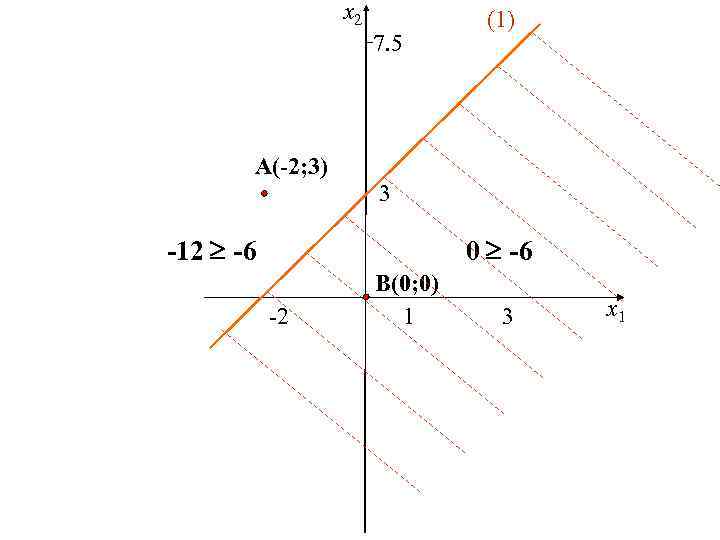
Построение первой полуплоскости (1) 3 х1 – 2 х2 – 6 Выбираем точки А(-2; 3) и В(0; 0), принадлежащие разным полуплоскостям. А(-2; 3) B(0; 0) 3·(-2) - 2· 3 -6 3· 0 - 2· 0 -6 -12 -6 0 -6 (неверно) (верно)

x 2 7. 5 (1) A(-2; 3) 3 -12 -6 0 -6 -2 B(0; 0) 1 3 x 1

Построение второй полуплоскости (2) 3 х1 + х2 3 Выбираем точки А(3; 3) и В(0; 0), принадлежащие разным полуплоскостям. А(3; 3) B(0; 0) 3· 3 + 3 3 3· 0 + 0 3 12 3 0 3 (верно) (неверно)

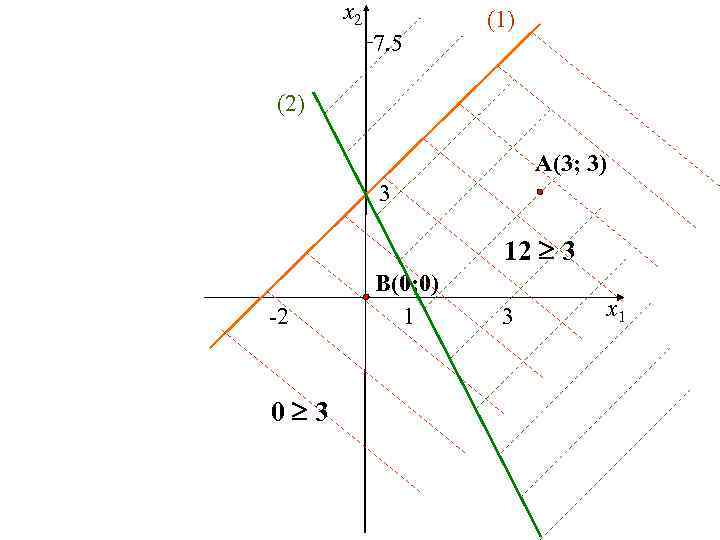x 2 7. 5 (1) (2) A(3; 3) 3 12 3 -2 0 3 B(0; 0) 1 3 x 1

Построение третьей полуплоскости (3) х1 3 Выбираем точки А(4; 3) и В(0; 0), принадлежащие разным полуплоскостям. А(4; 3) B(0; 0) 4 3 0 3 (неверно) (верно)

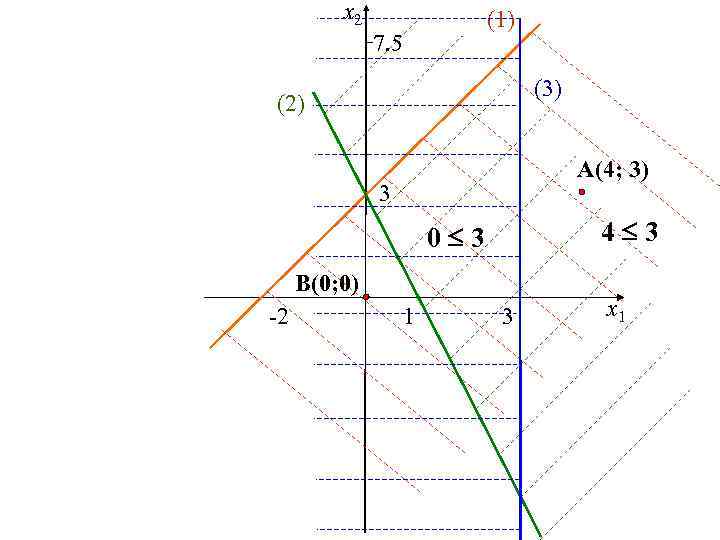x 2 (1) 7. 5 (3) (2) A(4; 3) 3 4 3 0 3 B(0; 0) -2 1 3 x 1

x 2 (1) 7. 5 (3) (2) 3 -2 1 3 x 1

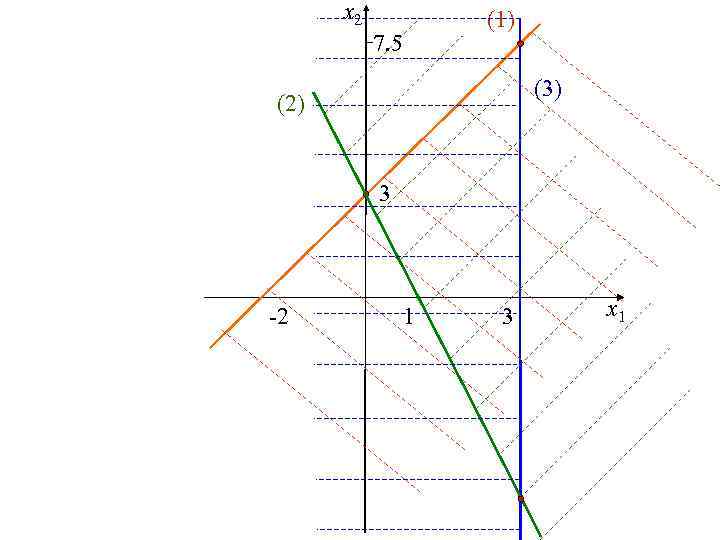
Построение области допустимых решений 2. Что на плоскости задает система неравенств? • По знакам неравенств определили область решений задачи. • Заменяя каждое ограничение равенствами, построили прямые.

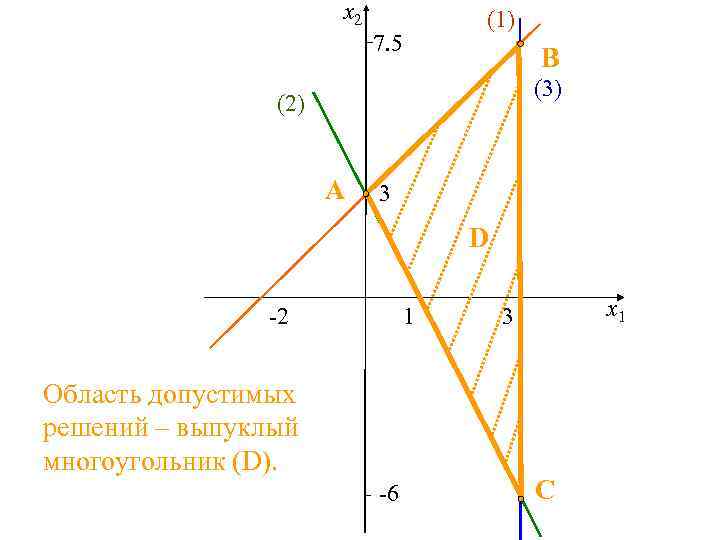x 2 (1) 7. 5 B (3) (2) A 3 D -2 1 Область допустимых решений – выпуклый многоугольник (D). -6 x 1 3 C

Построение области допустимых решений 1. Какие варианты ОДР возможны? 2. Получили ОДР, определенную системой ограничений задачи (заштрихованная на рисунке область ABC). • По знакам неравенств определили область решений задачи. • Заменяя каждое ограничение равенствами, построили прямые.

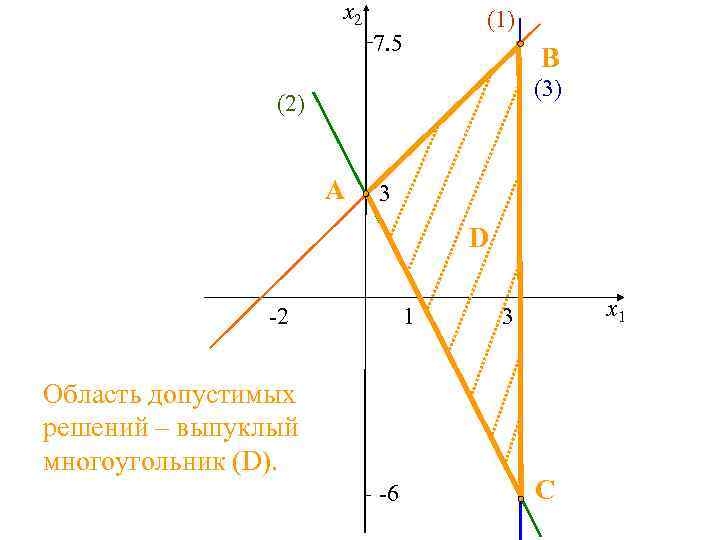x 2 (1) 7. 5 B (3) (2) A 3 D -2 1 Область допустимых решений – выпуклый многоугольник (D). -6 x 1 3 C

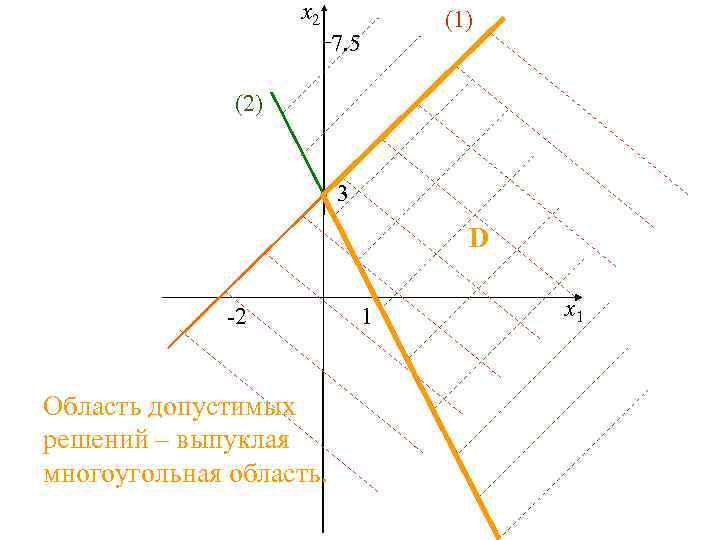x 2 (1) 7. 5 (2) 3 D -2 Область допустимых решений – выпуклая многоугольная область. 1 x 1

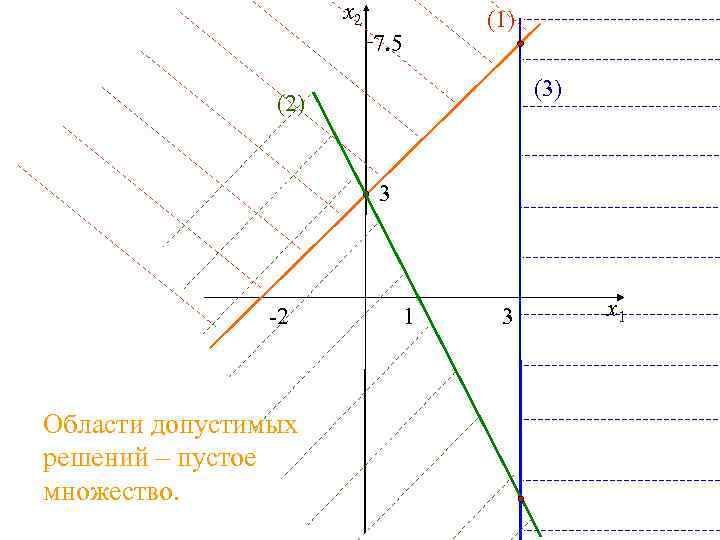x 2 (1) 7. 5 (3) (2) 3 -2 Области допустимых решений – пустое множество. 1 3 x 1

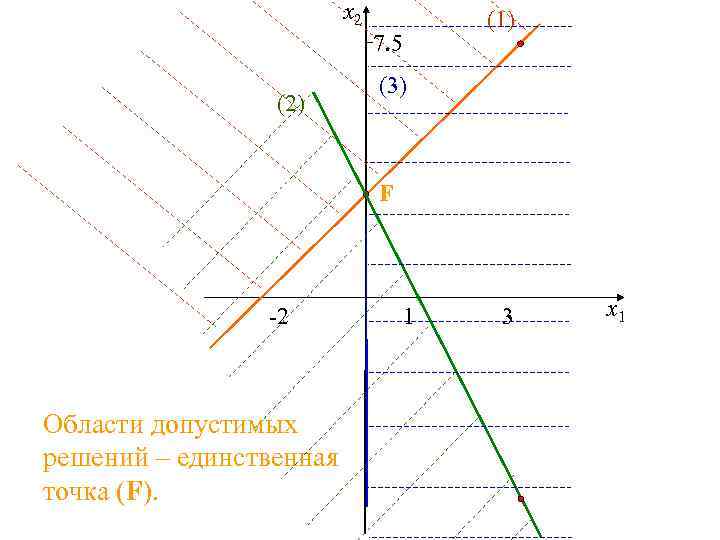x 2 (1) 7. 5 (2) (3) F -2 Области допустимых решений – единственная точка (F). 1 3 x 1

Построение направляющего вектора 1. В чем заключается геометрическая интерпретация целевой функции? • Как на плоскости построить вектор С = (с1, с2)? • Как на плоскости построить линии уровня целевой функции?

Построение направляющего вектора С = (2; 2) – вектор наискорейшего возрастания целевой функции. Всегда началом вектора является точка О(0; 0)!

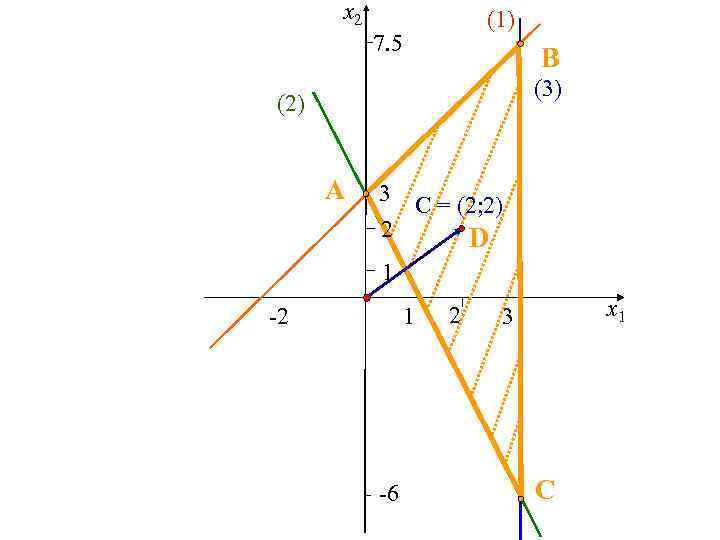x 2 (1) 7. 5 B (3) (2) A 3 2 С = (2; 2) D 1 -2 1 -6 2 x 1 3 C

Построение линии уровня А = (- 2; 2) – одна точка линии уровня. В = (0; 0) – вторая точка линии уровня.

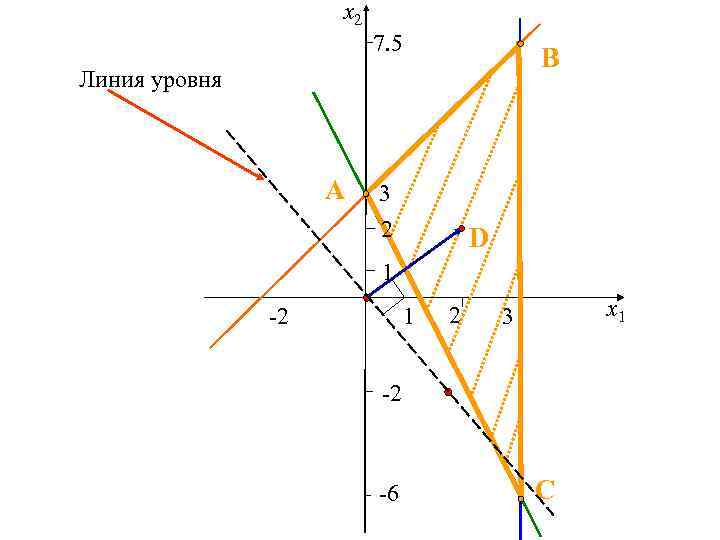x 2 7. 5 B Линия уровня A 3 2 D 1 -2 1 2 x 1 3 -2 -6 C

Определение оптимального плана 1. В чем заключается геометрическая интерпретация нахождения оптимального плана? • Как найти точку выхода? • Как найти координаты точки выхода?

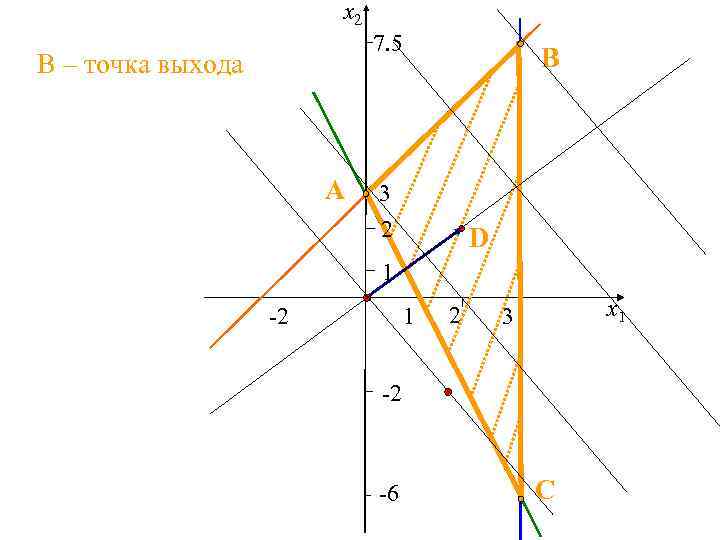x 2 7. 5 В – точка выхода A B 3 2 D 1 -2 1 2 x 1 3 -2 -6 C

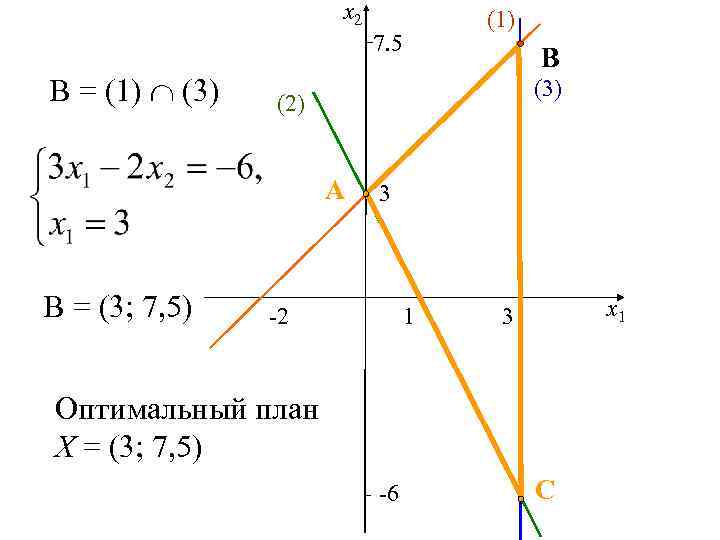x 2 (1) 7. 5 В = (1) (3) (2) A В = (3; 7, 5) B 3 -2 1 x 1 3 Оптимальный план X = (3; 7, 5) -6 C

Определение экстремального значения целевой функции X = (3; 7, 5) - оптимальный план при X = (3; 7, 5).