Геометрические задачи С 2 Угол между плоскостями

Геометрические задачи «С 2»

Угол между плоскостями

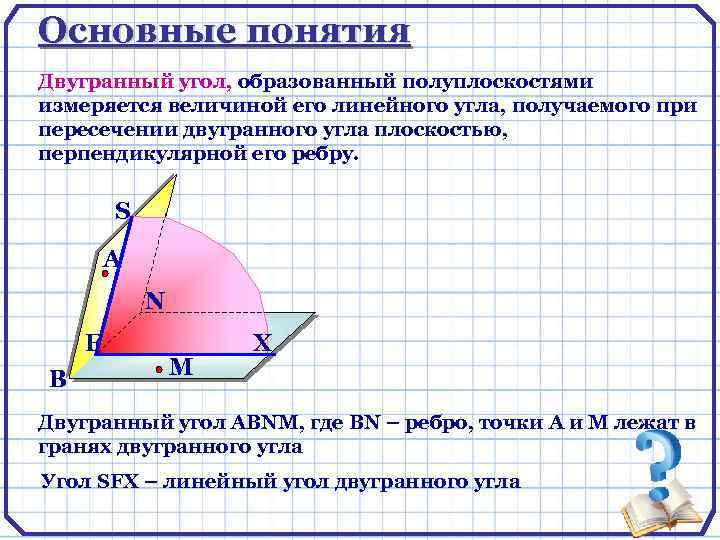Основные понятия Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру. S А N F В М X Двугранный угол АВNМ, где ВN – ребро, точки А и М лежат в гранях двугранного угла Угол SFX – линейный угол двугранного угла

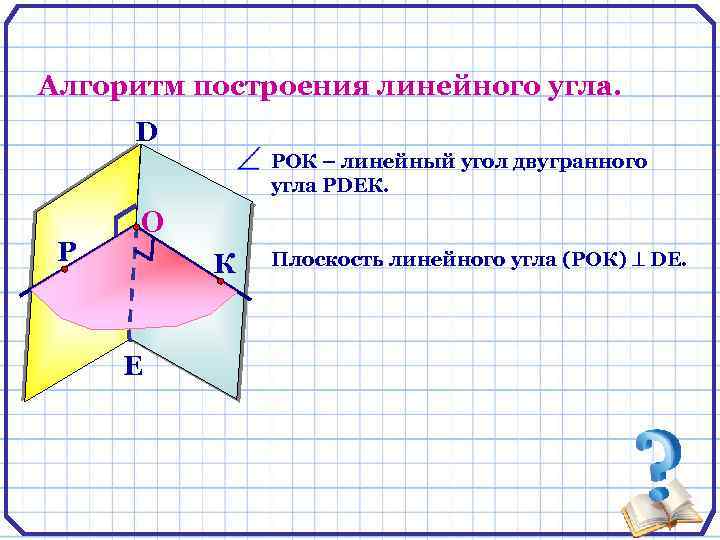Алгоритм построения линейного угла. D РОК – линейный угол двугранного угла РDEК. Р О К E Плоскость линейного угла (РОК) DE.

Угол между пересекающимися плоскостями можно вычислить: 1) Как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения; 2) Как угол треугольника, если удается включить линейный угол в некоторый треугольник; 3) Используя координатно –векторный метод; 4) Используя ключевые задачи.

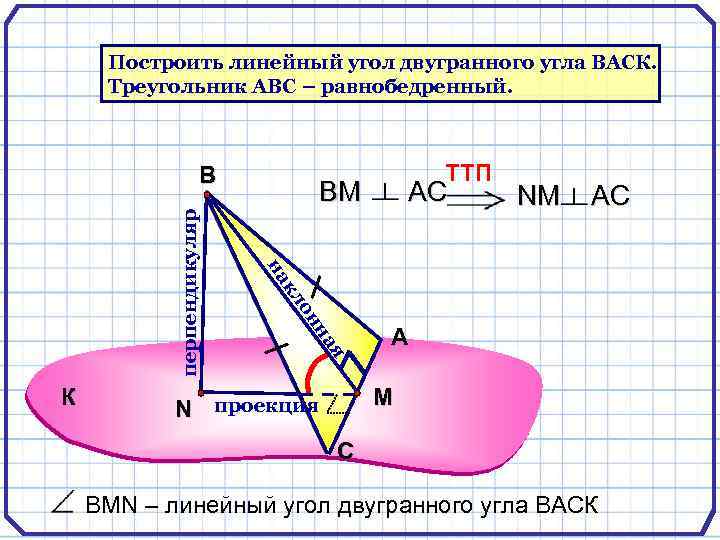Построить линейный угол двугранного угла ВАСК. Треугольник АВС – равнобедренный. ВМ АС NM AC нн о кл ая К TTП на перпендикуляр В А M N проекция С ВMN – линейный угол двугранного угла ВАСК

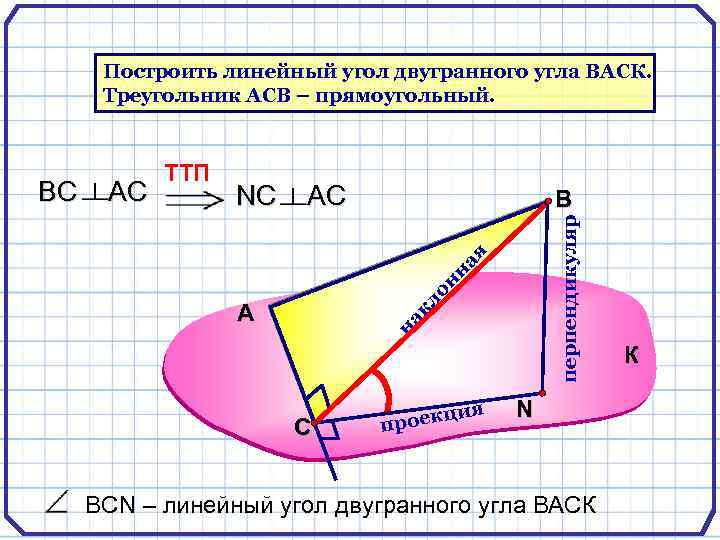Построить линейный угол двугранного угла ВАСК. Треугольник АCB – прямоугольный. AC В перпендикуляр NC я AC на кл он на BC TTП А С ия ц проек N ВСN – линейный угол двугранного угла ВАСК К

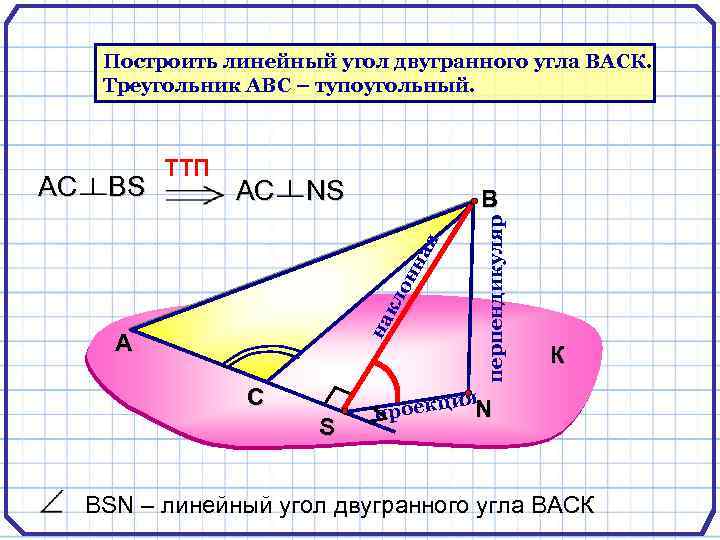Построить линейный угол двугранного угла ВАСК. Треугольник АВС – тупоугольный. NS В перпендикуляр AC кл он на я BS на AC TTП А С S К ия. N ц проек N ВSN – линейный угол двугранного угла ВАСК

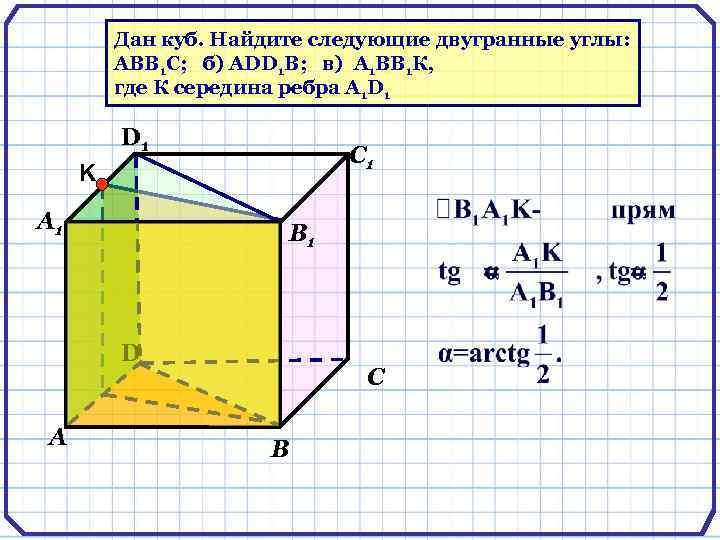Дан куб. Найдите следующие двугранные углы: АВВ 1 С; б) АDD 1 B; в) А 1 ВВ 1 К, где К середина ребра А 1 D 1 С 1 K А 1 В 1 D А С В

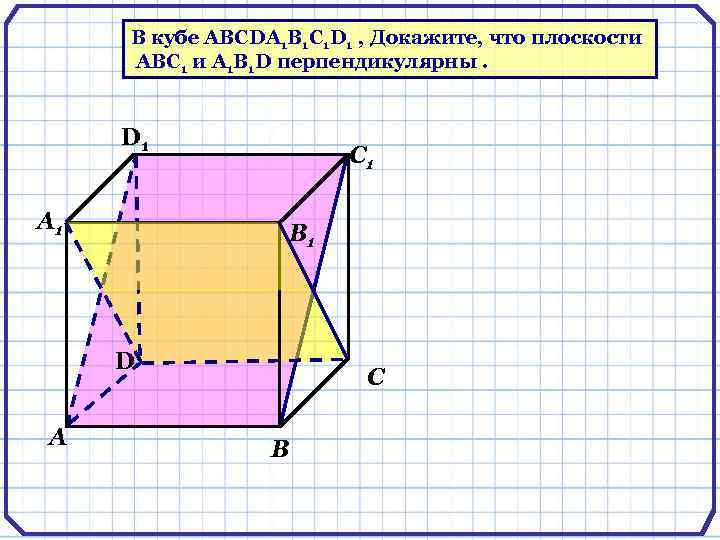В кубе ABCDA 1 B 1 C 1 D 1 , Докажите, что плоскости АВС 1 и А 1 В 1 D перпендикулярны. D 1 А 1 С 1 В 1 D А С В

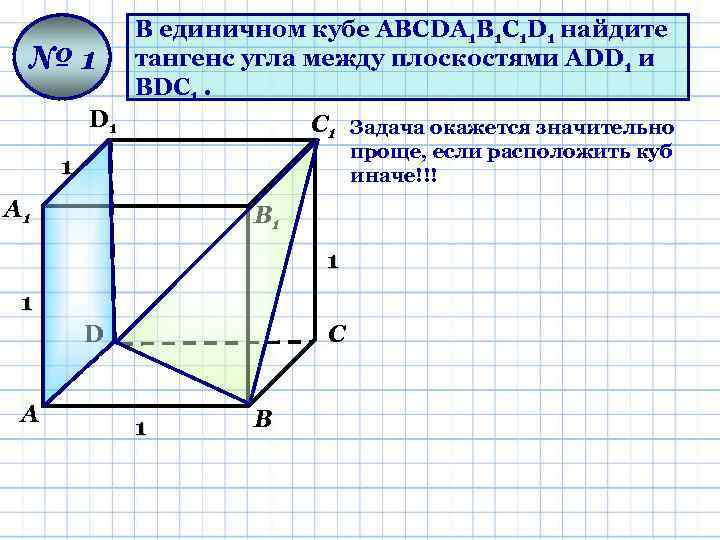№ 1 В единичном кубе АВСDА 1 В 1 С 1 D 1 найдите тангенс угла между плоскостями АDD 1 и ВDС 1. D 1 С 1 Задача окажется значительно проще, если расположить куб иначе!!! 1 А 1 В 1 1 1 D А С 1 В

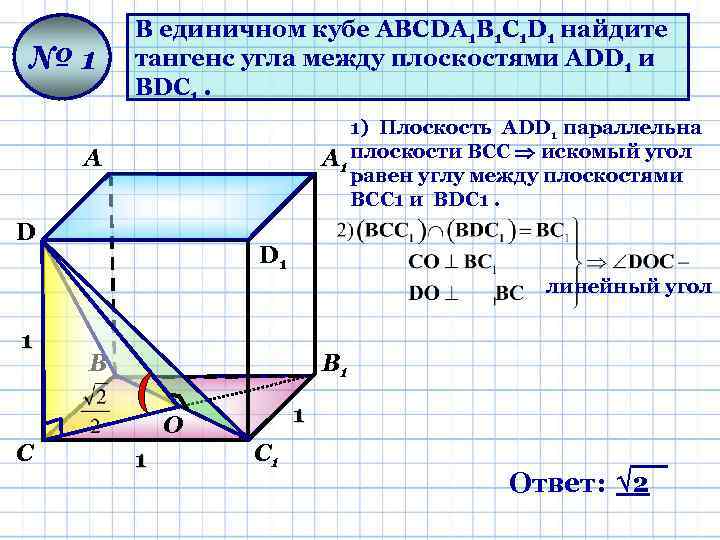№ 1 В единичном кубе АВСDА 1 В 1 С 1 D 1 найдите тангенс угла между плоскостями АDD 1 и ВDС 1. 1) Плоскость ADD 1 параллельна А 1 плоскости ВСС искомый угол равен углу между плоскостями ВСС 1 и ВDС 1. А D D 1 линейный угол 1 В В 1 1 О С 1 Ответ: 2

Критерии оценивания выполнения задания С 2 баллы Критерии оценивания 2 Правильный ход решения. Верно построен или описан искомый угол. Получен верный ответ. 1 1) Правильный ход решения. Получен верный ответ, но имеется ошибка в построении и описании искомого угла, не повлиявшая на ход решения 2) Правильный ход решения. Верно построен и описан искомый угол, но имеется ошибка в одном из вычислений, допущенная из-за невнимательности, в результате чего получен неверный ответ. 0 1) Ход решения правильный, но оно не доведено до конца, или решение отсутствует. Нет ответа. 2) Ход решения правильный, но имеются существенные ошибки в вычислениях, приведшие к неправильному ответу 3) Неправильный ход решения, приведший к неверному ответу 4) Верный ответ получен случайно при неверном решении или существенных ошибках в вычислениях.

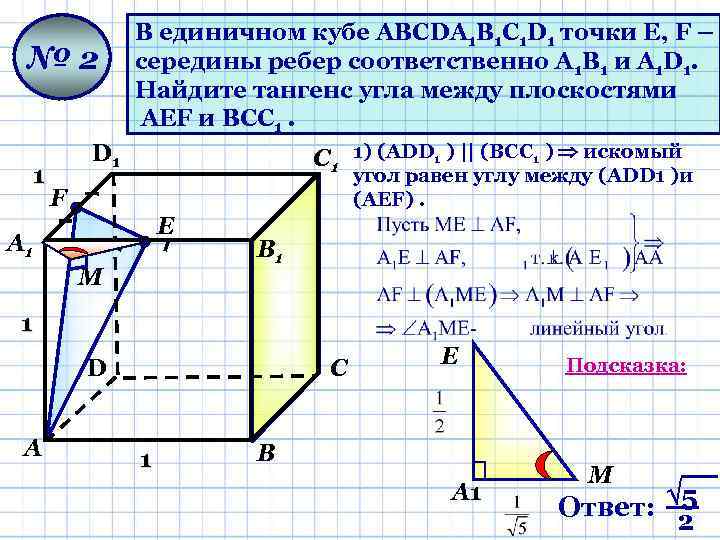№ 2 1 В единичном кубе АВСDА 1 В 1 С 1 D 1 точки Е, F – середины ребер соответственно А 1 В 1 и А 1 D 1. Найдите тангенс угла между плоскостями АЕF и ВСС 1. С 1 1) (ADD 1 ) || (ВСС 1 ) искомый D 1 угол равен углу между (АDD 1 )и (АЕF). F Е А 1 М В 1 1 D А С 1 Е В А 1 Подсказка: М Ответ: 5 2

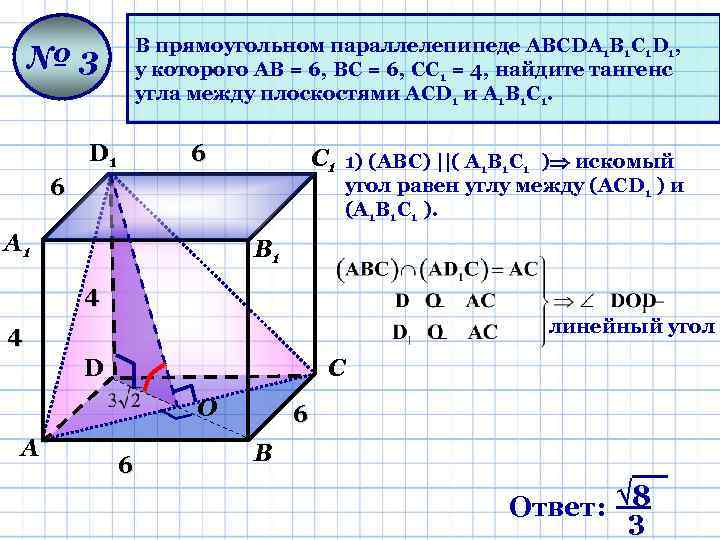В прямоугольном параллелепипеде АВСDА 1 В 1 С 1 D 1, у которого АВ = 6, ВС = 6, СС 1 = 4, найдите тангенс угла между плоскостями АСD 1 и А 1 В 1 С 1. № 3 D 1 6 С 1 1) (AВС) ||( А 1 В 1 С 1 ) искомый 6 угол равен углу между (АСD 1 ) и (А 1 В 1 С 1 ). А 1 В 1 4 линейный угол 4 D С О А 6 6 В Ответ: 8 3

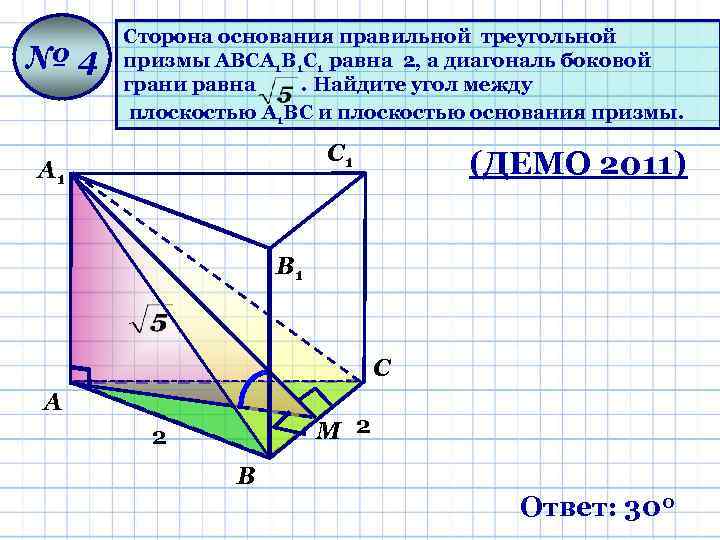№ 4 Сторона основания правильной треугольной призмы ABCA 1 B 1 C 1 равна 2, а диагональ боковой грани равна. Найдите угол между плоскостью A 1 BC и плоскостью основания призмы. С 1 А 1 (ДЕМО 2011) В 1 С А М 2 2 В Ответ: 300

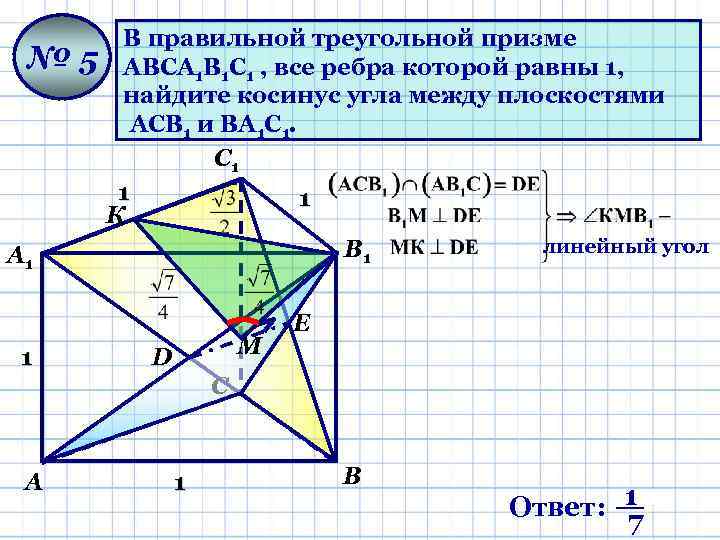№ 5 А 1 1 В правильной треугольной призме АВСА 1 В 1 С 1 , все ребра которой равны 1, найдите косинус угла между плоскостями АСВ 1 и ВА 1 С 1. С 1 1 1 К линейный угол В 1 М D Е С А 1 В Ответ: 1 1 7

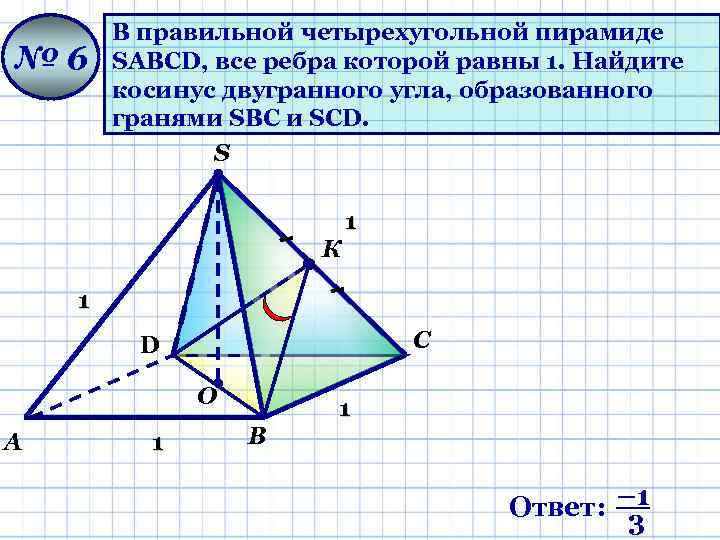№ 6 В правильной четырехугольной пирамиде SАВСD, все ребра которой равны 1. Найдите косинус двугранного угла, образованного гранями SВС и SCD. S 1 К 1 С D О А 1 1 В Ответ: – 1 3

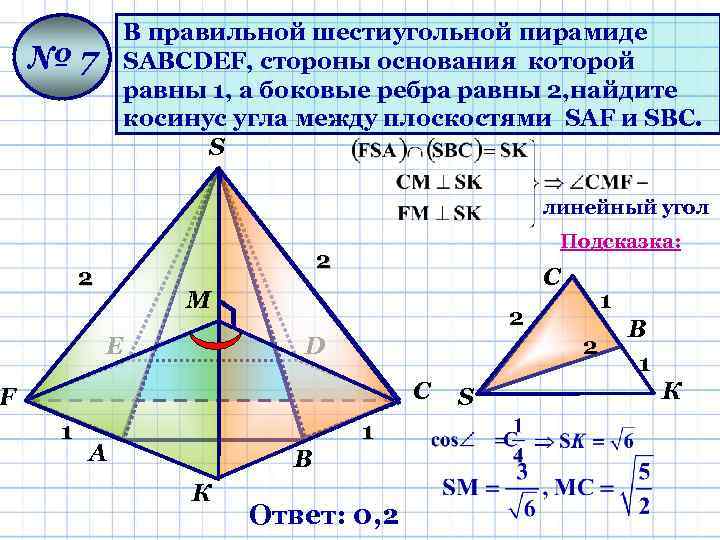В правильной шестиугольной пирамиде SАВСDЕF, стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между плоскостями SАF и SВС. S № 7 линейный угол Подсказка: 2 2 С М Е 2 D 2 С F 1 1 А В К 1 Ответ: 0, 2 S В 1 К

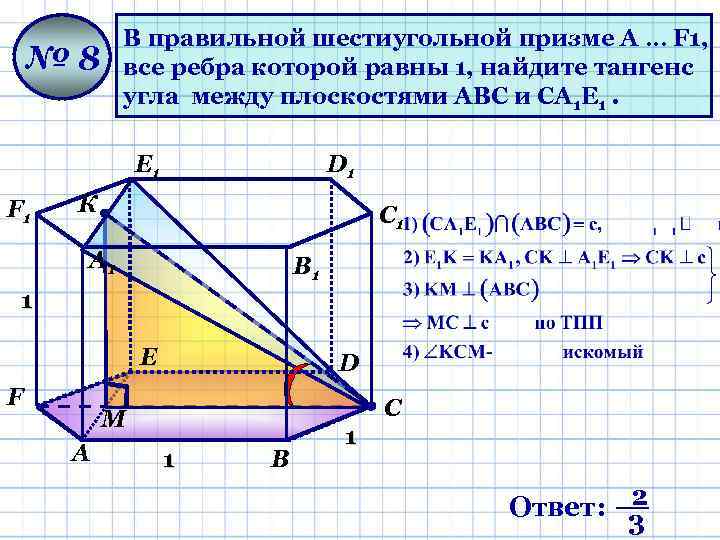В правильной шестиугольной призме A … F 1, все ребра которой равны 1, найдите тангенс угла между плоскостями AВС и CА 1 Е 1. № 8 Е 1 F 1 D 1 К С 1 А 1 В 1 1 Е F D С М А 1 В 1 2 Ответ: 3