Геометрические приложения определенного интеграла Вычисление площадей плоских

Геометрические приложения определенного интеграла

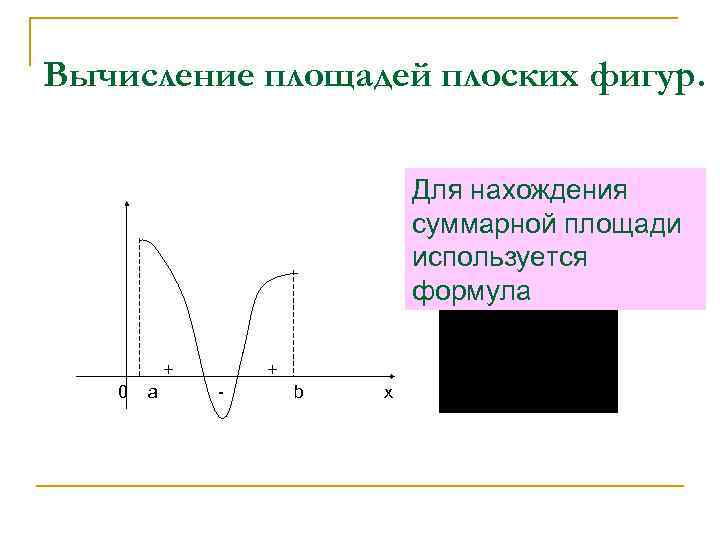Вычисление площадей плоских фигур. Для нахождения суммарной площади используется формула + 0 a + - b x

n Задача 1: Вычислить площадь области, ограниченной графиками функций y=f 1(x) и y=f 2(x) (f 1(x)≥f 2(x) или f 1(x)≤f 2(x) для всех точек области) и, возможно, прямыми x=a и x=b. Если область D задана системой неравенств то площадь области находится по формуле.

n n Если неравенства, определяющие область D, неизвестны, т. е. неизвестны a и b и неизвестно, какая из функций f 1(x) и f 2(x) больше на (a, b), то выполняем следующие операции. 1. Находим a и b как абсциссы точек пересечения графиков функций y=f 1(x) и y=f 2(x), т. е. решаем уравнение f 1(x)=f 2(x). 2. Исследуем знак разности f 1(x)-f 2(x) на [a, b]. Для этого достаточно вычислить значение f 1(x)-f 2(x) в какой-нибудь точке из (a, b). Если оно положительно, то f 1(x)≥f 2(x) и

n n Задача 2. Вычислить площадь области, ограниченной графиком функции, заданной параметрически y=y(t), x=x(t) и, возможно, прямыми x=a или y=b. Формула вычисления площади области в случае, когда уравнение линии задано параметрически: (1) 1. Вычисляем x=x’(t). 2 Из условий x=a или y=b находим границы 3. По формуле (1) находим искомую площадь.

Задача 3 Вычислить площадь области, ограниченной графиками функции. Формула вычисления площади области в полярных координатах: Если , и то эта формула принимает вид:

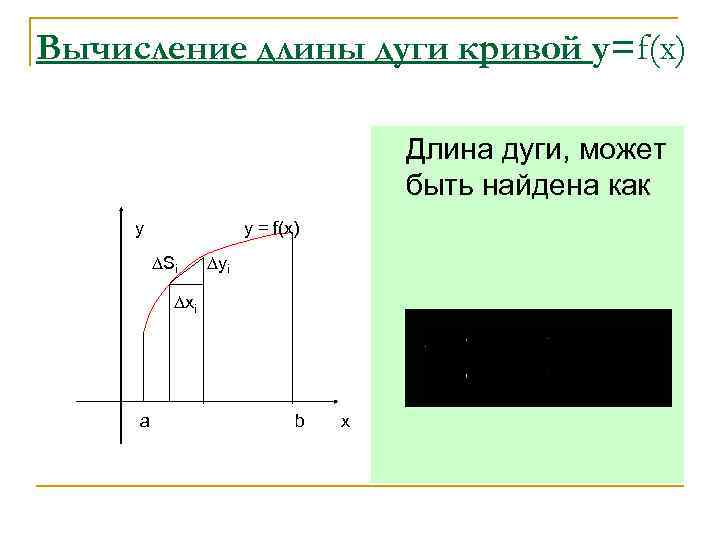Вычисление длины дуги кривой у=f(x) Длина дуги, может быть найдена как y y = f(x) Si yi xi a b x

Вычисление длины дуги кривой, заданной параметрически Если кривая задана уравнениями в параметрической форме где x=x(t), y=y(t) – кусочно-гладкие функции, то длина дуги L кривой вычисляется по формуле где и – значения параметра, соответствующие граничным точкам дуги.

Вычисление длины дуги кривой в полярных координатах Если кусочно-гладкая кривая задана уравнением в полярных координатах то длина дуги равна , (1), где и – значения , соответствующие граничным точкам дуги.

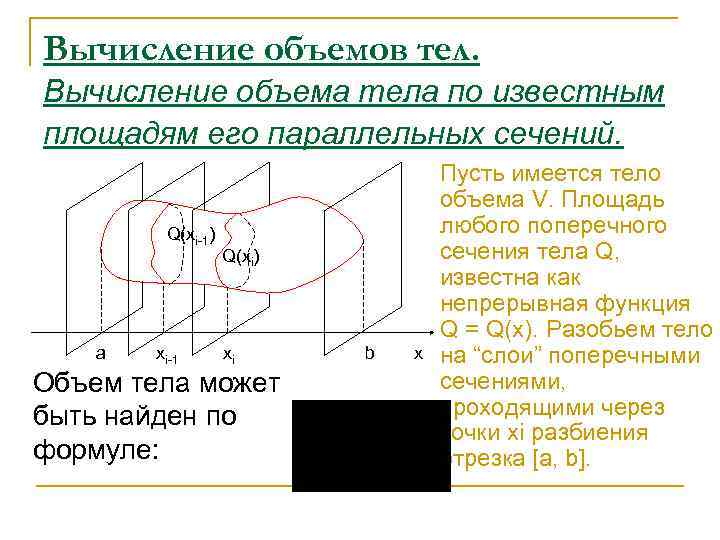Вычисление объемов тел. Вычисление объема тела по известным площадям его параллельных сечений. Q(xi-1) a xi-1 Q(xi) xi Объем тела может быть найден по формуле: b x Пусть имеется тело объема V. Площадь любого поперечного сечения тела Q, известна как непрерывная функция Q = Q(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки хi разбиения отрезка [a, b].

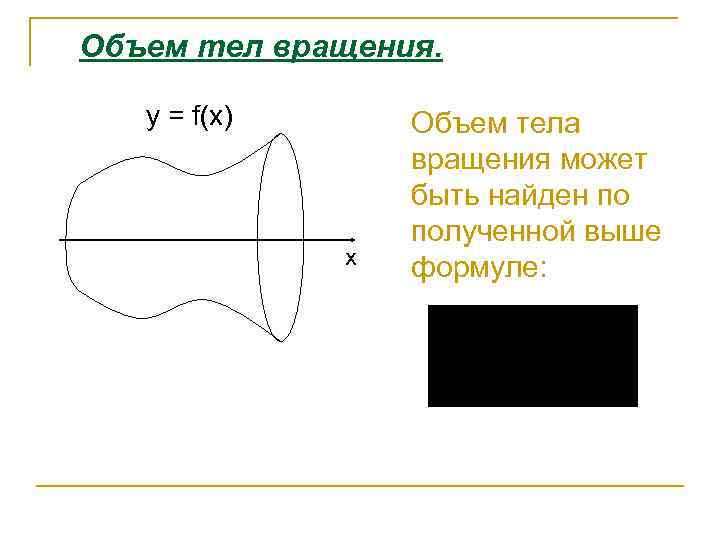Объем тел вращения. y = f(x) x Объем тела вращения может быть найден по полученной выше формуле:

q n Задача 1. Вычислить объем тела, образованного вращением области, ограниченного графиками функций y=f 1(x) и y=f 2(x) и, возможно, прямыми x=a и x=b, вокруг оси Ox. Объем тела, образованного вращением области, ограниченной кривыми y=u(x) и y=v(x) и прямыми x=a и x=b, где , т. е. области, определяемой системой неравенств вычисляется по формуле

n n Если неравенства, определяющие область D, неизвестны, т. е. неизвестны a и b и/или неизвестно, какая из функций f 1(x) и f 2(x) больше другой на отрезке [a, b], то выполняем следующие операции: а) находим a и b как абсциссы точек пересечения графиков функций y=f 1(x) и y=f 2(x), т. е. решаем уравнение f 1(x)=f 2(x); б) исследуем знак разности f 1(x)-f 2(x) на отрезке [a, b, ]. Для этого достаточно вычислить значение f 1(x)-f 2(x) в какой-нибудь точке из (a, b). Если оно положительно, то f 1(x)f 2(x) и, следовательно, u(x)=f 2(x) и v(x)=f 1(x). Если оно отрицательно, то f 1(x)f 2(x) и, следовательно, u(x)=f 1(x) и v(x)=f 2(x). Вычисляем объем по формуле

Площадь поверхности тела вращения. Определение: Площадью Мi B А xi Разобьем дугу АВ на n частей точками M 0, M 1, M 2 , … , Mn. поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения х ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных. Формула вычисления площади поверхности тела вращения.