«Геометрические преобразования пространства» Выполнили студенты группы С-11 Деев Ефим Исаков Илья Карпов Антон
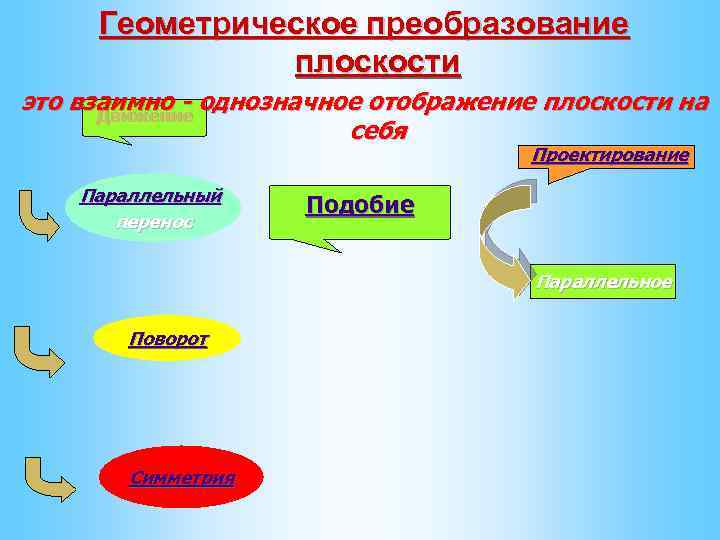
Геометрическое преобразование плоскости это взаимно - однозначное отображение плоскости на Движение себя Проектирование Параллельный перенос Подобие Параллельное Поворот Симметрия
Параллельным переносом на вектор ḡ называется отображение пространства на себя, при котором любая точка М переходит в такую М‘, что ММ‘= ḡ z Точка М(х; у; z) переходит в точку М(х+а; у+b; z+c), где а, b и с для всех точек (х; у; z) ḡ о • м' у х • м Параллельный перенос задается формулами: х‘=х+а; у‘=у+b; z‘=z+c
Параллельный перенос z о х Движение, сохраняющее направление, является параллельным переносом у
у' у х' β х Поворотом плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении о β – угол поворота Точка О-центр поворота
Поворот в пространстве Спутники вращаются вокруг планет Планеты вращаются вокруг солнца
«Симметрия является той идеей, посредством которой человек на протяжении веков пытается постичь и создать порядок, красоту и совершенство » Г. Вейль Центральная симметрия. Осевая симметрия Зеркальная симметрия
Отображение пространства на себя, при котором любая точка А переходит в симметричную к 1 • ей точку А 1 относительно данного центра О • А А А 1 • • о • К
Центральная симметрия в природе кактусы
М • ℓ О М 1 • Осевой симметрией с осью ℓ называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М 1 относительно оси ℓ
Осевая симметрия в архитектуре Библиотека им. Лермонтова г. Ставрополь
Осевая симметрия животного мира
Осевая симметрия в технике
Зеркальной симметрией(симметрией относительно плоскости) называется такое отображение пространства на себя, при котором любая точка Х переходит в симметричную ей относительно данной плоскости точку Х ' ●Х • ●Х'
Зеркальная симметрия в Природе
Преобразование фигуры F в фигуру F‘ называется преобразованием подобия, если при этом преобразовании расстояние между точками изменяется в одно и тоже число раз. А 1 В 1=k∙АВ С 1 Д 1=k∙СД В 1 k-КОЭФФИЦИЕНТ • В • ПОДОБИЯ • Д 1 А 1 • • С 1 • Д А • • С
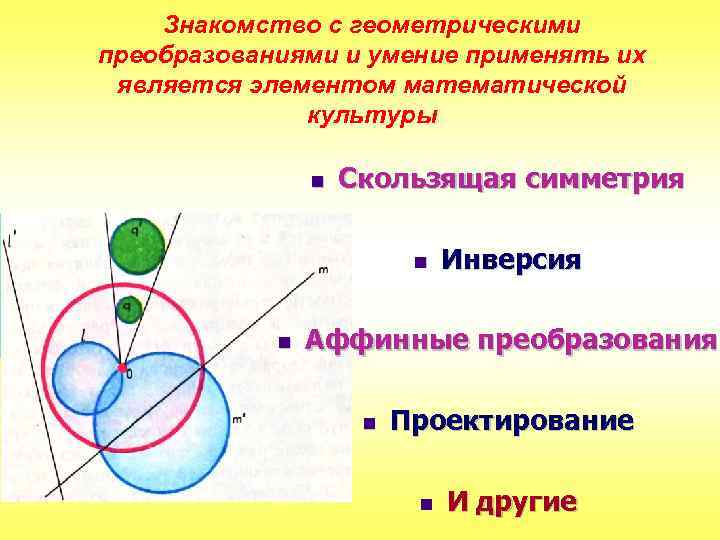
Знакомство с геометрическими преобразованиями и умение применять их является элементом математической культуры n Скользящая симметрия n n Инверсия Аффинные преобразования n Проектирование n И другие
Скачать презентацию Геометрические преобразования пространства Выполнили студенты группы С-11
Математика.ppt