ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Разработала: Семенова Н. В. Деление

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Разработала: Семенова Н. В.

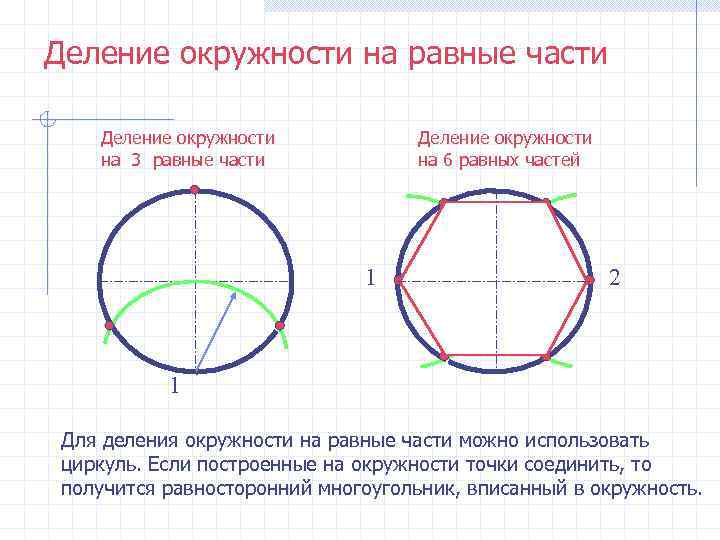
Деление окружности на равные части Деление окружности на 3 равные части на 6 равных частей 1 2 1 Для деления окружности на равные части можно использовать циркуль. Если построенные на окружности точки соединить, то получится равносторонний многоугольник, вписанный в окружность.

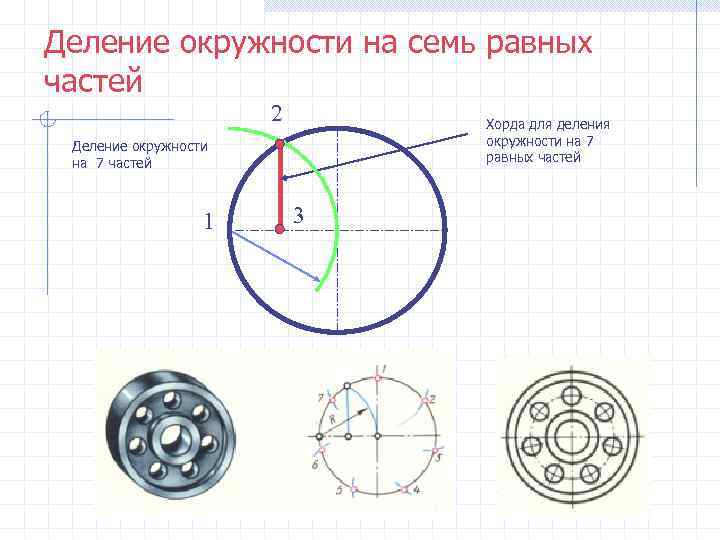
Деление окружности на семь равных частей 2 Хорда для деления Деление окружности на 7 частей равных частей 1 3

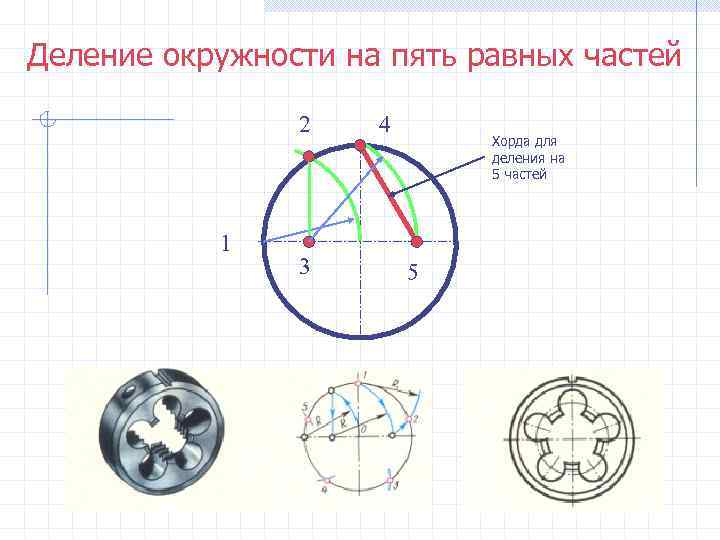
Деление окружности на пять равных частей 2 4 Хорда для деления на 5 частей 1 3 5

Примеры построений деления окружности Расчет длины хорды для деления окружности на равные части производится по формуле: L=Dk. D - диаметр окружности. k - коэффициент из таблицы. Например, для деления окружности диаметром 100 мм на 11 равных частей величина хорды будет вычислена по формуле. L=100 х 0, 282 =28, 2 мм

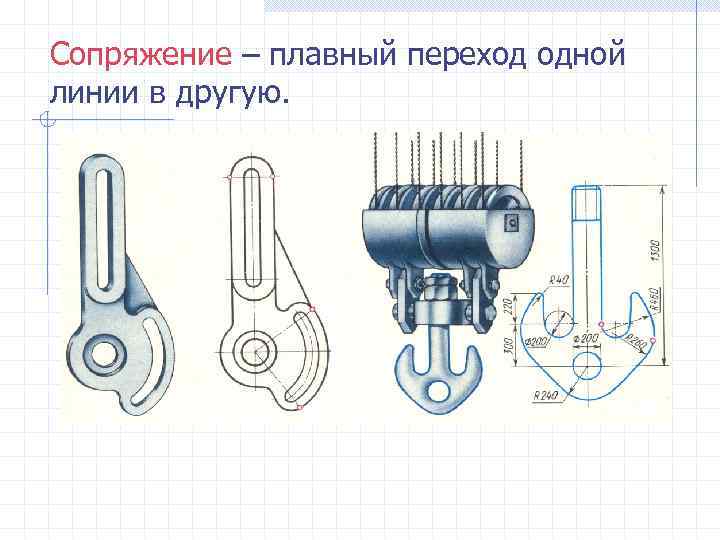
Сопряжение – плавный переход одной линии в другую.

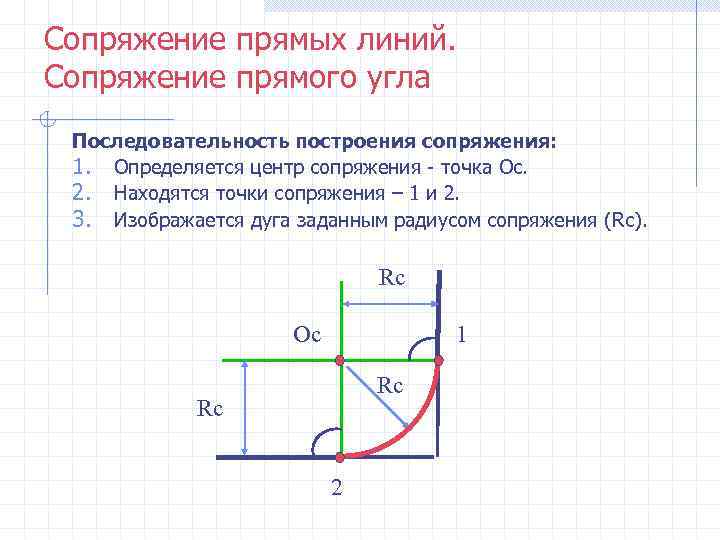
Сопряжение прямых линий. Сопряжение прямого угла Последовательность построения сопряжения: 1. Определяется центр сопряжения - точка Ос. 2. Находятся точки сопряжения – 1 и 2. 3. Изображается дуга заданным радиусом сопряжения (Rc). Rc Oс 1 Rc 2

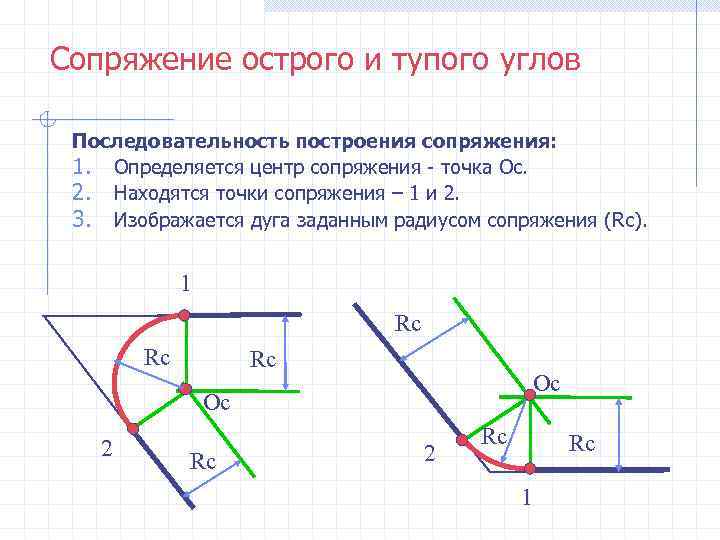
Сопряжение острого и тупого углов Последовательность построения сопряжения: 1. Определяется центр сопряжения - точка Ос. 2. Находятся точки сопряжения – 1 и 2. 3. Изображается дуга заданным радиусом сопряжения (Rc). 1 Rc Rc Ос 2 Rc 2 1

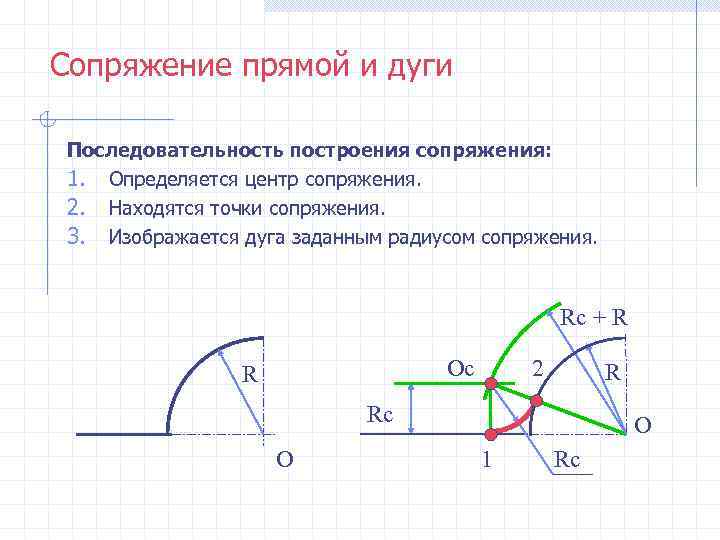
Сопряжение прямой и дуги Последовательность построения сопряжения: 1. Определяется центр сопряжения. 2. Находятся точки сопряжения. 3. Изображается дуга заданным радиусом сопряжения. Rc + R Ос 2 R Rc О 1 Rc

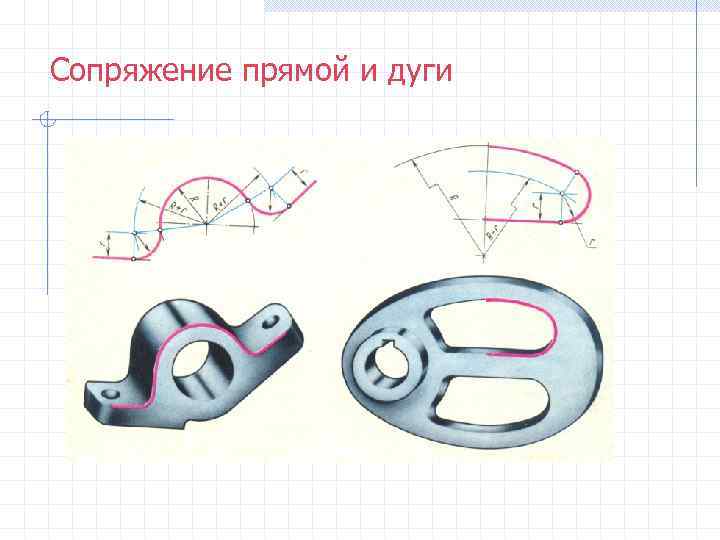
Сопряжение прямой и дуги

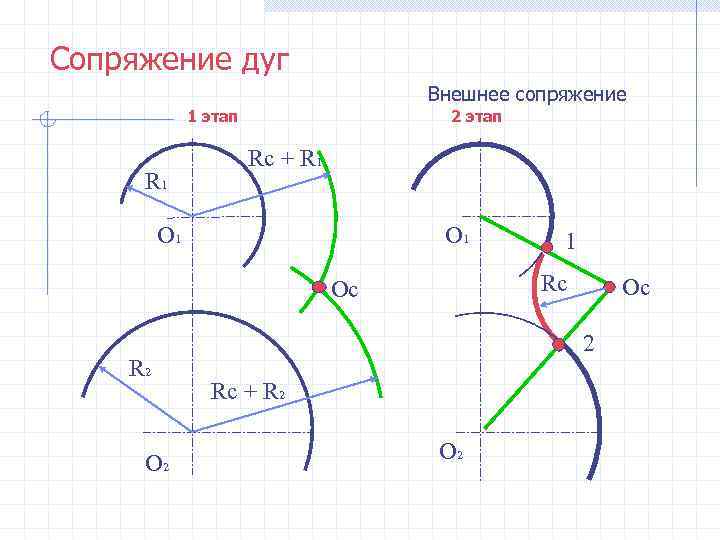
Сопряжение дуг Внешнее сопряжение 1 этап 2 этап Rc + R 1 О 1 Ос Rc Ос 2 R 2 Rc + R 2 О 2

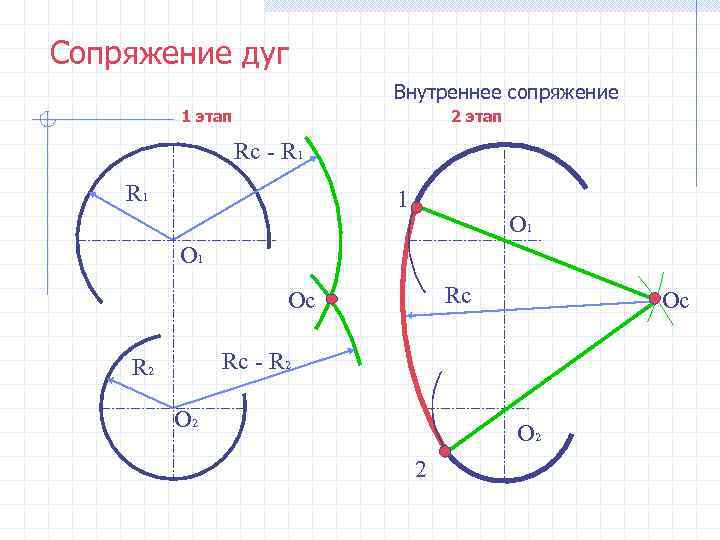
Сопряжение дуг Внутреннее сопряжение 1 этап 2 этап Rc - R 1 О 1 Ос Rc Ос R 2 Rc - R 2 О 2 2

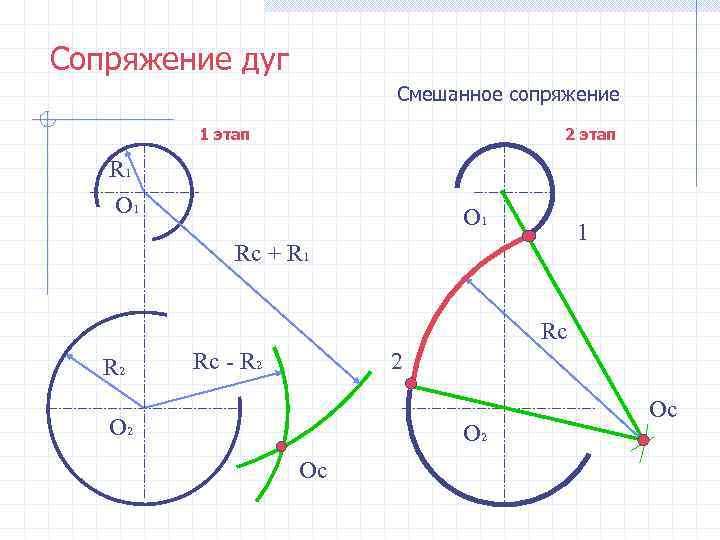
Сопряжение дуг Смешанное сопряжение 1 этап 2 этап R 1 О 1 1 Rc + R 1 Rc R 2 Rc - R 2 2 Ос О 2 Ос

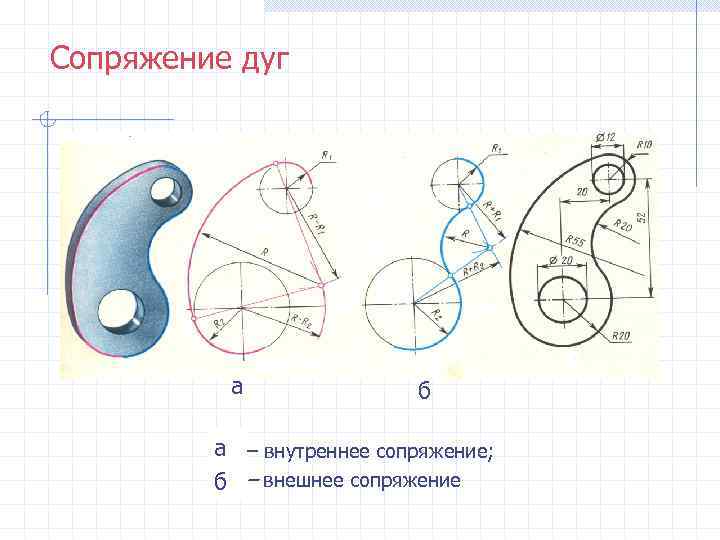
Сопряжение дуг а б а б – внутреннее сопряжение; б в – внешнее сопряжение

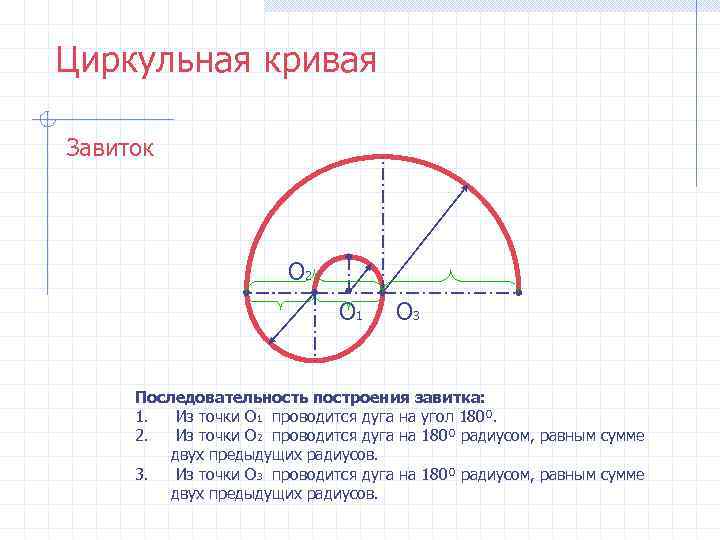
Циркульная кривая Завиток О 2 О 1 О 3 Последовательность построения завитка: 1. Из точки О 1 проводится дуга на угол 180º. 2. Из точки О 2 проводится дуга на 180º радиусом, равным сумме двух предыдущих радиусов. 3. Из точки О 3 проводится дуга на 180º радиусом, равным сумме двух предыдущих радиусов.

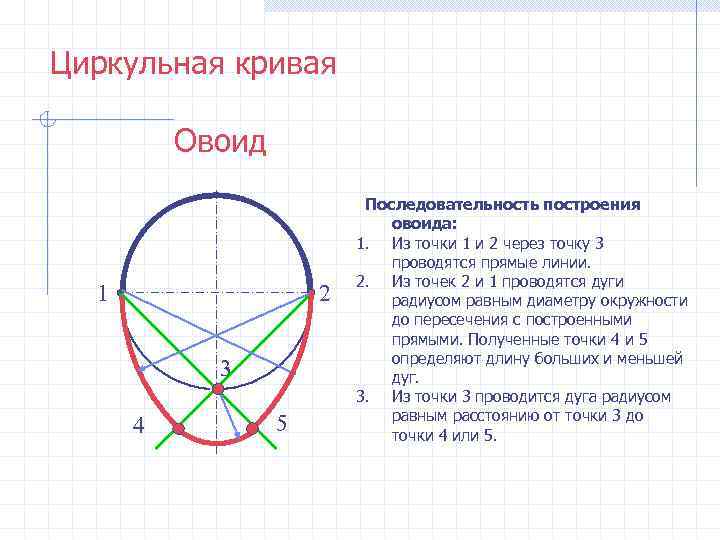
Циркульная кривая Овоид Последовательность построения овоида: 1. Из точки 1 и 2 через точку 3 проводятся прямые линии. 2. Из точек 2 и 1 проводятся дуги 1 2 радиусом равным диаметру окружности до пересечения с построенными прямыми. Полученные точки 4 и 5 определяют длину больших и меньшей 3 дуг. 3. Из точки 3 проводится дуга радиусом равным расстоянию от точки 3 до 4 5 точки 4 или 5.

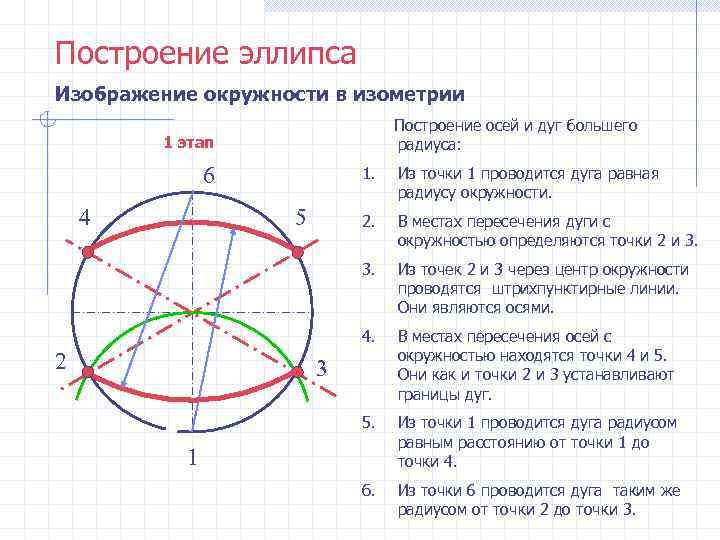
Построение эллипса Изображение окружности в изометрии Построение осей и дуг большего 1 этап радиуса: 6 1. Из точки 1 проводится дуга равная радиусу окружности. 4 5 2. В местах пересечения дуги с окружностью определяются точки 2 и 3. 3. Из точек 2 и 3 через центр окружности проводятся штрихпунктирные линии. Они являются осями. 4. В местах пересечения осей с 2 окружностью находятся точки 4 и 5. 3 Они как и точки 2 и 3 устанавливают границы дуг. 5. Из точки 1 проводится дуга радиусом равным расстоянию от точки 1 до 1 точки 4. 6. Из точки 6 проводится дуга таким же радиусом от точки 2 до точки 3.

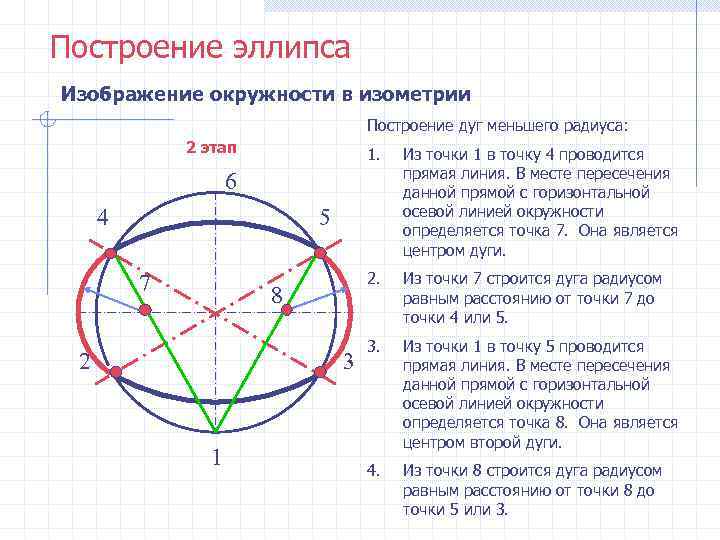
Построение эллипса Изображение окружности в изометрии Построение дуг меньшего радиуса: 2 этап 1. Из точки 1 в точку 4 проводится прямая линия. В месте пересечения 6 данной прямой с горизонтальной 4 5 осевой линией окружности определяется точка 7. Она является центром дуги. 7 2. Из точки 7 строится дуга радиусом 8 равным расстоянию от точки 7 до точки 4 или 5. 3. Из точки 1 в точку 5 проводится 2 3 прямая линия. В месте пересечения данной прямой с горизонтальной осевой линией окружности определяется точка 8. Она является центром второй дуги. 1 4. Из точки 8 строится дуга радиусом равным расстоянию от точки 8 до точки 5 или 3.

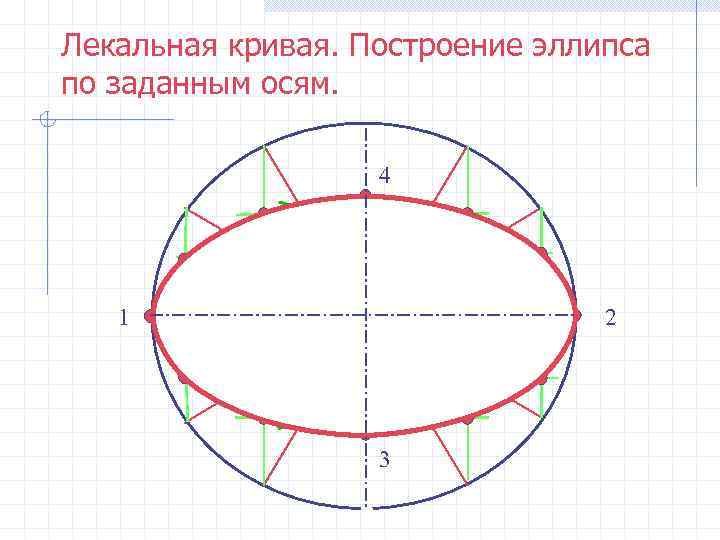
Лекальная кривая. Построение эллипса по заданным осям. 4 1 2 3

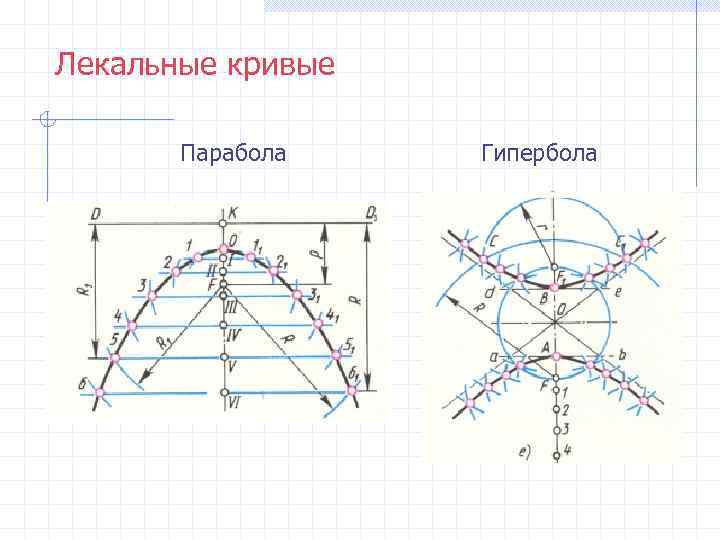
Лекальные кривые Парабола Гипербола

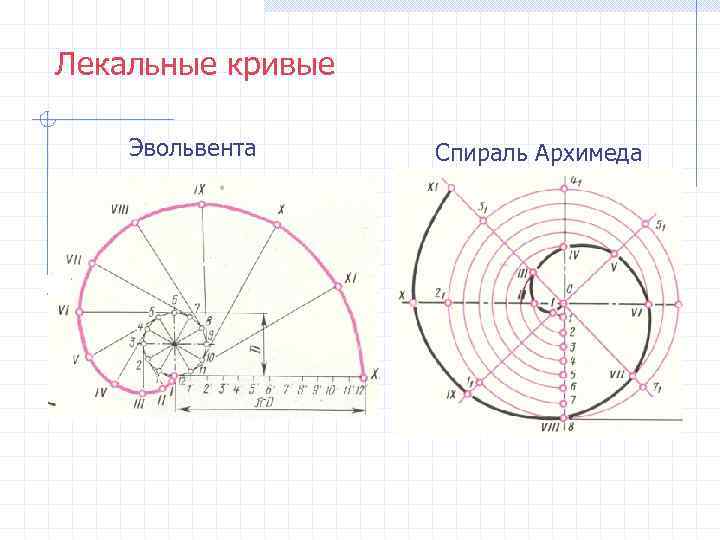
Лекальные кривые Эвольвента Спираль Архимеда

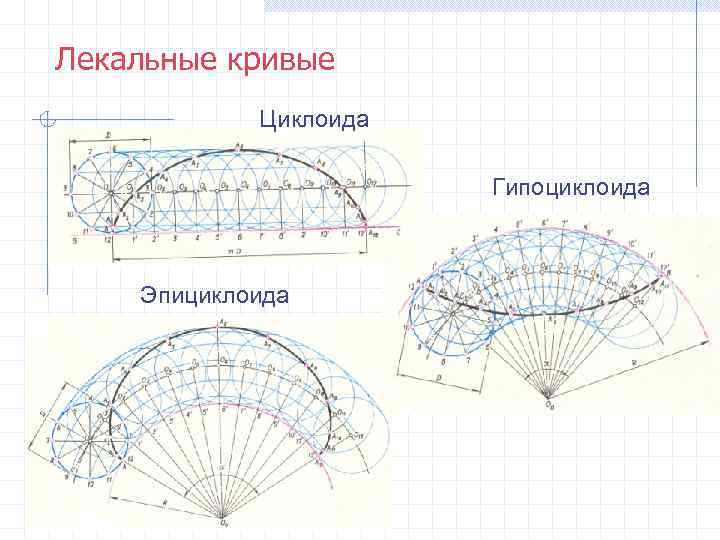
Лекальные кривые Циклоида Гипоциклоида Эпициклоида