 Геометрические фракталы L-системы Домашних И. А.
Геометрические фракталы L-системы Домашних И. А.
 Геометрические фракталы •
Геометрические фракталы •
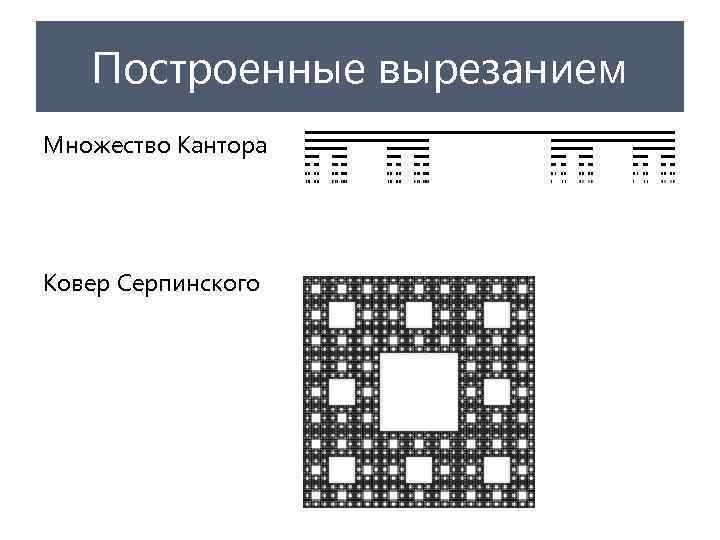 Построенные вырезанием Множество Кантора Ковер Серпинского
Построенные вырезанием Множество Кантора Ковер Серпинского
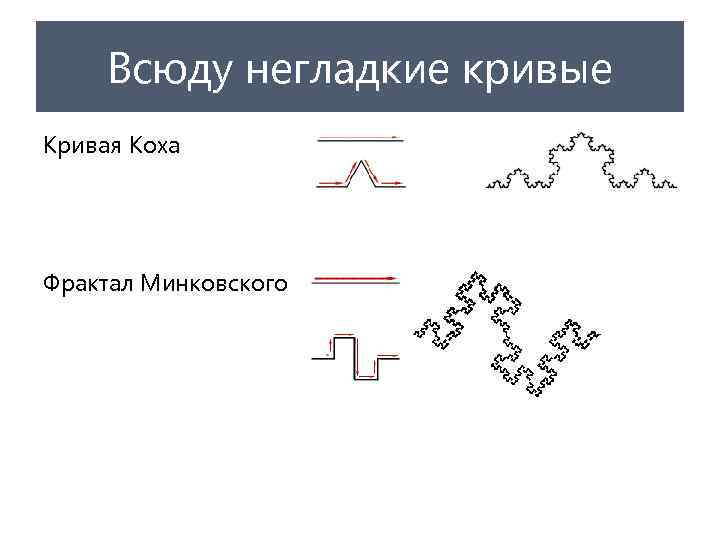 Всюду негладкие кривые Кривая Коха Фрактал Минковского
Всюду негладкие кривые Кривая Коха Фрактал Минковского
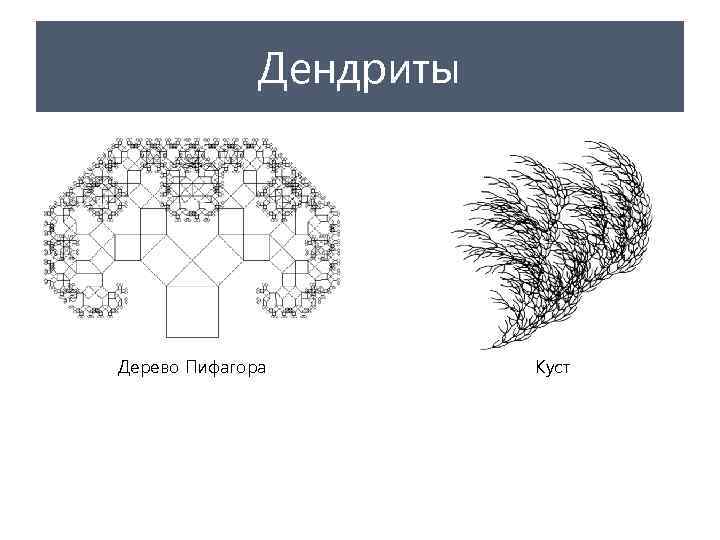 Дендриты Дерево Пифагора Куст
Дендриты Дерево Пифагора Куст
 Драконы Дракон Хартера-Хэйтуэя
Драконы Дракон Хартера-Хэйтуэя
 L-системы Понятие появилось в 1968 году благодаря Аристриду Линденмайеру Использовались § при изучении формальных языков § в биологических моделях селекции С помощью L-систем можно строить многие геометрические фракталы, в том числе § снежинку Коха § множество Кантора § дракона Хартера-Хэйтуэя L-системы широкого применяются в компьютерной графике для построения фрактальных деревьев и растений
L-системы Понятие появилось в 1968 году благодаря Аристриду Линденмайеру Использовались § при изучении формальных языков § в биологических моделях селекции С помощью L-систем можно строить многие геометрические фракталы, в том числе § снежинку Коха § множество Кантора § дракона Хартера-Хэйтуэя L-системы широкого применяются в компьютерной графике для построения фрактальных деревьев и растений
 Состав L-системы 1. Алфавит 2. Аксиома – слово инициализации 3. Набор порождающих правил – преобразования слова на каждой итерации
Состав L-системы 1. Алфавит 2. Аксиома – слово инициализации 3. Набор порождающих правил – преобразования слова на каждой итерации
![Пример L-системы 1. Алфавит: F f + - ] [ 2. Аксиома: F 3. Пример L-системы 1. Алфавит: F f + - ] [ 2. Аксиома: F 3.](https://present5.com/presentation/1/1153304_443144479.pdf-img/1153304_443144479.pdf-9.jpg) Пример L-системы 1. Алфавит: F f + - ] [ 2. Аксиома: F 3. Правила: a. F преобразуется в некоторое слово b. Любой другой символ не изменяется Обновление букв предполагается одновременным
Пример L-системы 1. Алфавит: F f + - ] [ 2. Аксиома: F 3. Правила: a. F преобразуется в некоторое слово b. Любой другой символ не изменяется Обновление букв предполагается одновременным
 Turtle-графика Используется для визуализации L-систем Черепашка (точка) движется по экрану в некотором направлении дискретными шагами § либо прочерчивая свой след § либо перемещаясь без следа Состояние черепашки § (х, у) – координаты черепашки § а – угол, направление, в котором черепашка смотрит Черепашка интерпретирует и выполняет последовательность команд, задаваемых кодовым словом Кодовое слово - результат работы L-системы
Turtle-графика Используется для визуализации L-систем Черепашка (точка) движется по экрану в некотором направлении дискретными шагами § либо прочерчивая свой след § либо перемещаясь без следа Состояние черепашки § (х, у) – координаты черепашки § а – угол, направление, в котором черепашка смотрит Черепашка интерпретирует и выполняет последовательность команд, задаваемых кодовым словом Кодовое слово - результат работы L-системы
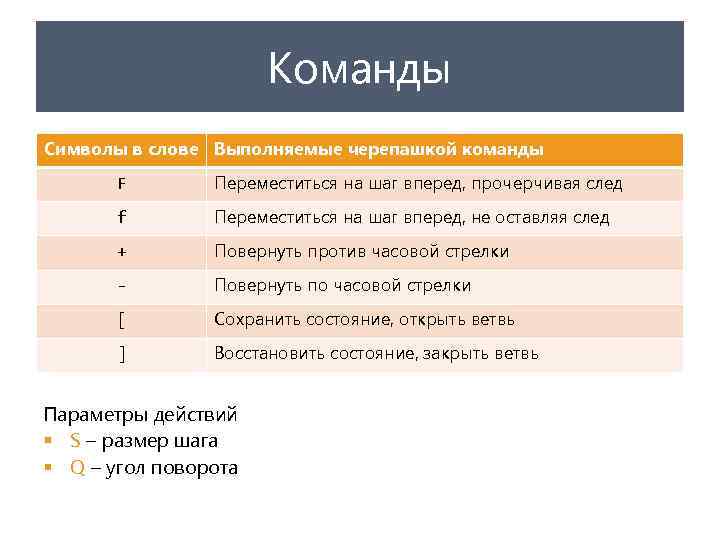 Команды Символы в слове Выполняемые черепашкой команды F Переместиться на шаг вперед, прочерчивая след f Переместиться на шаг вперед, не оставляя след + Повернуть против часовой стрелки - Повернуть по часовой стрелки [ Сохранить состояние, открыть ветвь ] Восстановить состояние, закрыть ветвь Параметры действий § S – размер шага § Q – угол поворота
Команды Символы в слове Выполняемые черепашкой команды F Переместиться на шаг вперед, прочерчивая след f Переместиться на шаг вперед, не оставляя след + Повернуть против часовой стрелки - Повернуть по часовой стрелки [ Сохранить состояние, открыть ветвь ] Восстановить состояние, закрыть ветвь Параметры действий § S – размер шага § Q – угол поворота
 Построение множества Кантора n=0 • n=1 F F n=2 f F F f f f F
Построение множества Кантора n=0 • n=1 F F n=2 f F F f f f F
 Построение снежинки Коха n=0 • n=1 F F-F++F-F
Построение снежинки Коха n=0 • n=1 F F-F++F-F
 Построение дракона n=0 F n=1 +F--F+ n=2 +(-F++F-)--(+F--F+)+ n=3 +(-(-F++F-)++(+F--F+)-)—(+(-F++F-)--(+F--F+)+)+ Имеется 2 разные замены: (-F++F-) и (+F--F+) Поэтому требуется несколько порождающих правил
Построение дракона n=0 F n=1 +F--F+ n=2 +(-F++F-)--(+F--F+)+ n=3 +(-(-F++F-)++(+F--F+)-)—(+(-F++F-)--(+F--F+)+)+ Имеется 2 разные замены: (-F++F-) и (+F--F+) Поэтому требуется несколько порождающих правил
 Построение дракона
Построение дракона
![Построение деревьев n=0 n=1 n=2 F F[+F][-F][+F[+F][-F]][-F[+F][-F]] Построение деревьев n=0 n=1 n=2 F F[+F][-F][+F[+F][-F]][-F[+F][-F]]](https://present5.com/presentation/1/1153304_443144479.pdf-img/1153304_443144479.pdf-16.jpg) Построение деревьев n=0 n=1 n=2 F F[+F][-F][+F[+F][-F]][-F[+F][-F]]
Построение деревьев n=0 n=1 n=2 F F[+F][-F][+F[+F][-F]][-F[+F][-F]]
 Спасибо за внимание
Спасибо за внимание