Geometric Sequences
Today’s Objectives • Concept of convergence and divergence • Sum to infinity of a geometric progression
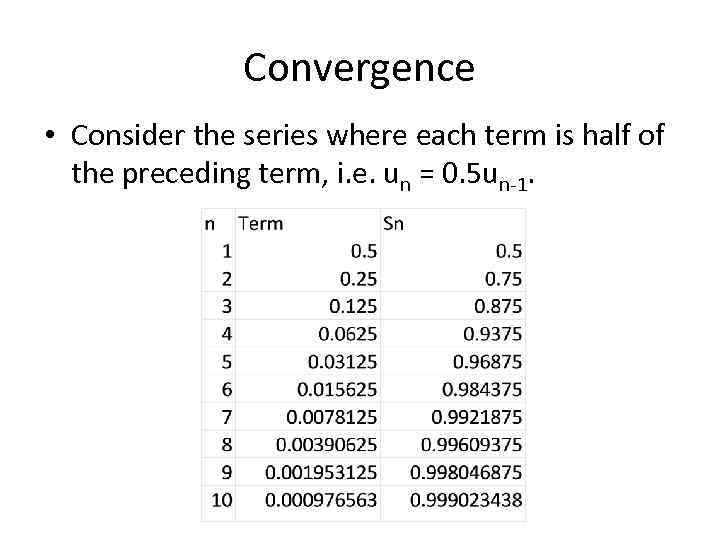
Convergence • Consider the series where each term is half of the preceding term, i. e. un = 0. 5 un-1.
Convergence • We can see that for this series the sum of the series converges to the value of 1. • This series is therefore convergent. • This series is actually a GP with first term a = 0. 5 and common ratio r = 0. 5.
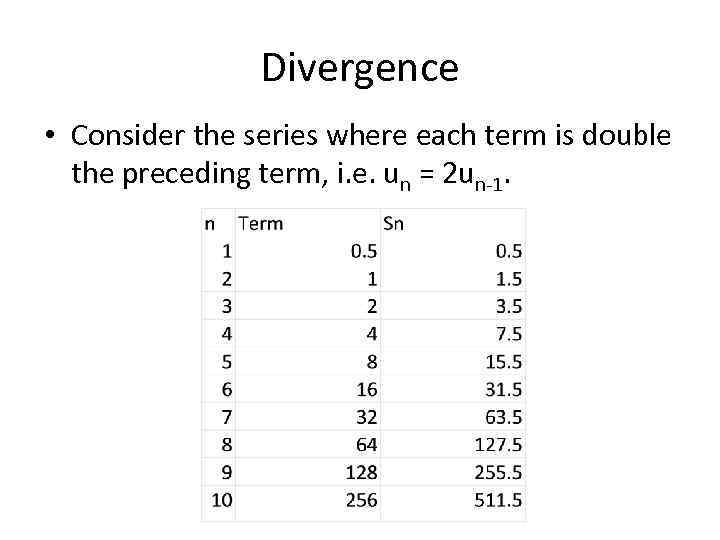
Divergence • Consider the series where each term is double the preceding term, i. e. un = 2 un-1.
Divergence • We can see that for this series the sum of the series continual increases and does not converge. • This series is therefore divergent. • This series is actually a GP with first term a = 0. 5 and common ratio r = 2.
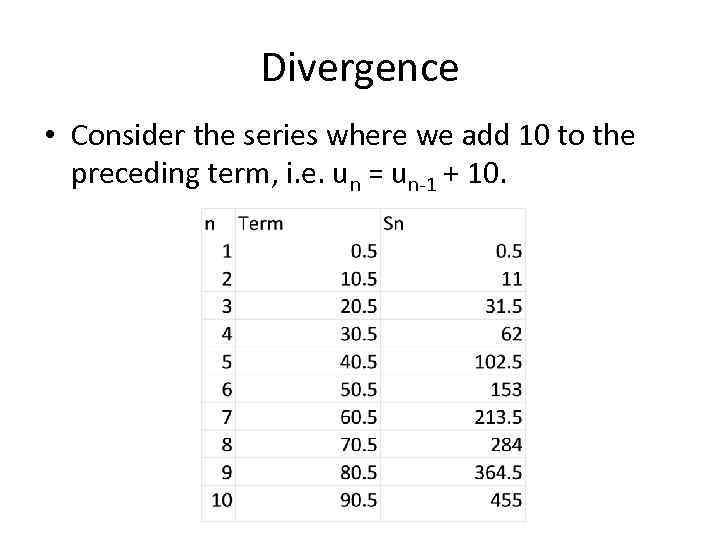
Divergence • Consider the series where we add 10 to the preceding term, i. e. un = un-1 + 10.
Divergence • We can see that for this series the sum of the series continual increases and does not converge. • This series is therefore divergent. • This series is actually an AP with first term a = 0. 5 and common difference d = 10.
Sum to infinity • What happens to the above series if we keep increasing n up to infinity? • Convergent series will continue to converge and divergent series will continue to diverge. • Can we generalise from the above examples?
Sum to infinity of APs • The last example above was an AP and it was divergent. This is true for all APs. • Since, for an AP, we are continual adding or continually subtracting, as n increases so the sum to n increases or decreases depending on whether the common difference is positive or negative respectively. • So when n → ∞, – S∞ → ∞ when d > 0 – S∞ → –∞ when d < 0
Sum to infinity of GPs • The first two examples above were GPs but the first was convergent and the second was divergent. • What was the difference between the two examples? • In the first example the common ratio r < 1 • In the second example the common ratio r > 1
Sum to infinity of GPs • Consider the formula for the sum of the first n terms of a GP: • Now consider the value of rn as n → ∞ for |r| < 1 and for |r| > 1
Sum to infinity of GPs • For |r| < 1, i. e. – 1 < r < 1:
Sum to infinity of GPs • For |r| > 1, i. e. r < – 1 or r > 1:
Sum to infinity of GPs • Hence,
Arithmetic mean • If 3 numbers, say p 1, p 2 and p 3, are in arithmetic progression the middle number p 2 is the arithmetic mean of p 1 and p 3. • Since if p 1 = a then p 2 = a + d and p 3 = a + 2 d then: • Hence the arithmetic mean of x and y is:
Geometric mean • If 3 numbers, say p 1, p 2 and p 3, are in geometric progression the middle number p 2 is the geometric mean of p 1 and p 3. • Since if p 1 = a then p 2 = ar and p 3 = ar 2 then: • Hence the geometric mean of x and y is:
Example 1 • To determine if a series converges or diverges, first establish if it is an AP or a GP then, if it is a GP, find the common ratio: • See hand written solution.
Example 2 • Find the condition on x so that the following series converges: • Now evaluate the series when x = 1. 5. • See hand written solution.
Example 3 • Express the recurring decimal 0. 15 7 6 as a fraction in its lowest terms. • See hand written solution.
Example 4 • The 3 rd term of a convergent GP is the arithmetic mean of the 1 st and 2 nd terms. Find the common ratio and, if the first term is 1, find the sum to infinity. • See hand written solution.
In summary • A series is convergent if its sum approaches a specific value. • A series is divergent if its sum approaches infinity (+/-). • All APs are divergent and so the sum to infinity is +/- infinity. • For GPs:
In summary • The arithmetic mean of x and y is: • The geometric mean of x and y is:
Скачать презентацию Geometric Sequences Today s Objectives Concept of
03 Geometric Progressions Sum to Infinity.pptx