ГЕОДЕЗИЯ ЛЕКЦИИ часть 2 2 курс 4 семестр

ГЕОДЕЗИЯ ЛЕКЦИИ (часть 2) 2 курс 4 семестр

5. Определение координат нескольких точек 5. 1. Задача Ганзена В задаче Ганзена находят координаты двух точек P и Q по известным координатам двух пунктов A и B и четырем углам, измеренным на определяемых точках (рис. 15), т. е. задача Ганзена является сдвоенной обратной угловой засечкой. Исходные данные: XA, YA, XB, YB. Измеренные элементы: β 1, β 2, β 3, β 4. Неизвестные элементы: XP, YP, XQ, YQ. Аналитическое решение. Известно несколько способов решения задачи Ганзена; приведем краткое изложение одного из них. 1. Решить обратную задачу между пунктами A и B, т. е. , вычислить длину b отрезка AB и дирекционный угол αAB направления AB.

Рис. 15. Схема задачи Ганзена 2. Ввести условную единицу длины, равную длине l отрезка PQ ; l = 1. 000. 3. Вычислить отрезки S'1 = AP, S'3 = AQ, S'2 = BP, S'4 = BQ в условных единицах с использованием теоремы синусов сначала для треугольника PAQ, затем для треугольника PBQ:

(5. 1) 4. Вычислить в условных единицах длину b' отрезка AB из треугольника QAB по теореме косинусов: (5. 2) и для контроля - из треугольника PAB: (5. 3)

5. Вычислить масштабный коэффициент k: k = b / b' и перевести все вычисленные расстояния в реальные единицы длины 6. Вычислить угол φ из треугольника QAB по теореме косинусов (5. 4) 7. Вычислить угол ψ из треугольника PAB по теореме косинусов: (5. 5)

8. Вычислить дирекционный угол направления AQ: (5. 6) и решить прямую геодезическую задачу с пункта A на точку Q : (5. 7) 9. Вычислить дирекционный угол направления BP (5. 8) αBP = αBA - φ и решить прямую геодезическую задачу с пункта B на точку P: (5. 9)

Расположение исходных пунктов и определяемых точек может быть таким, что отрезки PQ и AB будут пересекаться (рис. 16). Ход решения задачи остается таким же, только изменятся обозначения углов и сторон. Кроме того, доказано, что в этом варианте положение точек P и Q определяется в несколько раз точнее, чем в общем варианте. Рис. 16. Вариант задачи Ганзена

5. 2. Линейно-угловой ход 5. 2. 1 Классификация линейно-угловых ходов Для определения координат нескольких точек можно применить различные способы; наиболее распространенными из них являются линейно-угловой ход, система линейно-угловых ходов, триангуляция, трилатерация и некоторые другие. Линейно-угловой ход представляет собой последовательность полярных засечек, в которой измеряются горизонтальные углы и расстояния между соседними точками (рис. 17). Рис. 17. Схема разомкнутого линейно-углового хода

Исходными данными в линейно-угловом ходе являются координаты XA, YA пункта A и дирекционный угол αBA линии BA, который называется начальным исходным дирекционным углом; этот угол может задаваться неявно через координаты пункта B. Измеряемые величины - это горизонтальные углы β 1, β 2, . . . , βk-1, βk и расстояния S 1, S 2, Sk-1, Sk. Известны также ошибка измерения углов mβ и относительная ошибка измерения расстояний m. S / S = 1 / T. Дирекционные углы сторон хода вычисляют последовательно по известным формулам передачи дирекционного угла через угол поворота - для левых углов: (5. 10) - для правых углов : (5. 11)

Координаты пунктов хода получают из решения прямой геодезической задачи сначала от пункта A к пункту 2, затем от пункта 2 к пункту 3 и так далее до конца хода. 1. Разомкнутый ход (рис. 17): исходные пункты с известными координатами и исходные дирекционные углы есть в начале и в конце хода. 2. Замкнутый линейно-угловой ход (рис. 18) - начальный и конечный пункты хода совмещены; один пункт хода имеет известные координаты и называется исходным пунктом; на этом пункте должно быть исходное направление с известным дирекционным углом, и измеряется примычный угол между этим направлением и направлением на второй пункт хода. 3. Висячий линейно-угловой ход (рис. 17) имеет исходный пункт с известными координатами и исходный дирекционный угол только в начале хода. 4. Свободный линейно-угловой ход не имеет исходных пунктов и исходных дирекционных углов ни в начале, ни в конце хода.

По точности измерения горизонтальных углов и расстояний линейно-угловые ходы делятся на две большие группы: теодолитные ходы и полигонометрические ходы. В теодолитных ходах горизонтальные углы измеряют с ошибкой не более 30"; относительная ошибка измерения расстояний m. S/S колеблется от 1/1000 до 1/3000. В полигонометрических ходах горизонтальные углы измеряют с ошибкой от 0, 4" до 10", а относительная ошибка измерения расстояний m. S/S : от 1/5000 до 1/300 000. По точности измерений полигонометрические ходы делятся на два разряда и четыре класса Рис. . 18. Схема замкнутого линейно-углового хода

5. 2. 2. Вычисление координат пунктов разомкнутого линейно-углового хода Каждый определяемый пункт линейно-углового хода имеет две координаты X и Y, которые являются неизвестными и которые нужно найти. Общее количество пунктов в ходе обозначим через n, тогда количество неизвестных будет 2 ( n - 2 ), так как у двух пунктов (исходных начального и конечного) координаты известны. Подсчитаем, сколько измерений выполняется в разомкнутом линейно-(n - 1) сторон хода, всего получается (2 n - 1) измерений (рис. 17). Разность между количеством выполненных измерений и количеством необходимых измерений равна: (2 n - 1) - 2(n - 2) = 3.

В геодезических построениях каждое избыточное измерение порождает какое-либо условие, поэтому количество условий равно количеству избыточных измерений; в разомкнутом линейно-угловом ходе должны выполняться три условия: условие дирекционных углов и два координатных условия. Условие дирекционных углов. Вычислим последовательно дирекционные углы всех сторон хода, используя формулу передачи дирекционного угла на последующую сторону хода: (5. 12) и (5. 13) Это - математическая запись первого геометрического условия в разомкнутом линейно-угловом ходе. Для правых углов поворота оно запишется так:

(5. 14) Сумма углов, подсчитанная по формулам (5. 13) и (5. 14), называется теоретической суммой углов хода. Сумма измеренных углов вследствие ошибок измерений, как правило, отличается от теоретической суммы на некоторую величину, называемую угловой невязкой и обозначаемую fβ: (5. 15) Допустимое значение угловой невязки можно рассматривать как предельную ошибку суммы измеренных углов (5. 16) Одним из этапов уравнивания является введение поправок в измеренные величины с целью приведения их в соответствие с геометрическими условиями. Обозначим поправку в измеренный угол Vβ и запишем условие:

(5. 17) откуда следует, что: (5. 18) В уравнении (5. 18) n неизвестных, и для его решения необходимо на поправки Vβ наложить (n-1) дополнительных условий. Наиболее простым вариантом таких условий будет: т. е. все поправки в измеренные углы одинаковы. В этом случае решение уравнения (5. 18) получается в виде: (5. 19)

Исправленные значения углов вычисляются по формуле: (5. 20) По исправленным углам поворота вычисляют дире- кционные углы всех сторон хода; совпадение вычисленного и заданного значений конечного исходного дирекционного угла является контролем прави льности обработки угловых измерений. Координатные условия. Решая последовательно прямую геодезическую задачу, вычислим приращения координат по каждой стороне хода ΔXi и ΔYi. Координаты пунктов хода получим по формулам:

или (5. 21) Аналогичная формула для суммы приращений ΔY имеет вид: (5. 22) Вследствие ошибок измерения сторон и упрощенного способа распределения угловой невязки суммы вычисленных приращений координат в общем случае не будут равны теоретическим суммам; возникают так называемые координатные невязки хода: (5. 23)

по которым вычисляют абсолютную невязку хода: (5. 24) и затем относительную невязку хода: (5. 25) Поправки в приращения координат вычисляют по формулам: (5. 26) которые соответствуют условию "поправки в приращения координат пропорциональны длинам сторон". Рассмотренный способ обработки измерений в линейно-угловом ходе можно назвать способом последовательного распределения невязок.

Строгое уравнивание линейно-углового хода выполняется по методу наименьших квадратов. После уравнивания одиночного линейно-углового хода ошибки положения его пунктов неодинаковы. Они возрастают от начала и конца хода к его середине, и наибольшую ошибку положения имеет пункт в середине хода. В случае приближенного уравнивания эта ошибка оценивается половиной абсолютной невязки хода fs. При строгом уравнивании хода производится сплошная оценка точности, т. е. вычисляются ошибки положения каждого пункта хода, ошибки дирекционных углов всех сторон хода, а также ошибки уравненных значений углов и сторон хода.

5. 2. 3. Вычисление координат пунктов замкнутого линейно-углового хода Вычисление координат пунктов в замкнутом линейно-угловом ходе выполняется в том же порядке, что и в разомкнутом ходе. Отличие состоит в вычислении теоретических сумм углов и приращений координат. Если в замкнутом ходе измерялись внутренние углы, то: Σβ = 180°∙(n – 2) если внешние, то Σβ = 180°∙(n + 2) и ΣΔX = 0; ΣΔY = 0.

5. 2. 4. Привязка линейно-угловых ходов Под привязкой разомкнутого линейно-углового хода понимают включение в ход двух пунктов с известными координатами (это начальный и конечный исходные пункты хода) и измерение на этих пунктах углов между направлением с известными дирекционными углами (αнач и αкон) и первой (последней) стороной хода. Эти углы называются примычными. Как уже отмечалось ранее, если на начальном или (и) конечном пункте хода примычный угол не измеряется, то имеет место частичная (полная) координатная привязка хода. Привязка замкнутого линейно-углового хода - это включение в ход одного пункта с известными координатами и измерение на этом пункте примычного угла, т. е. угла между направлением с известным дирекционным углом и первой стороной хода.

Кроме этих стандартных ситуаций встречаются случаи, когда линейно-угловой ход начинается или заканчивается на пункте с неизвестными координатами. В таких случаях возникает дополнительно задача определения координат этого пункта. Самый простой способ определения координат одного пункта - геодезические засечки: если вблизи определяемого пункта есть несколько известных пунктов, то, выполнив k угловых и (или) линейных измерений (k>2), можно вычислить искомые координаты по стандартным алгоритмам. Если такой возможности нет, то возникают особые случаи привязки; рассмотрим некоторые из них.

Снесение координат с вершины знака на землю. На рис. 19: P - определяемый пункт, T 1, T 2, T 3 - пункты с известными координатами, которые можно использовать лишь в качестве визирных целей. Рис. 19. Схема к определению элементов редукции

приближенное решение можно получить по конечным формулам, приведенным ниже: - вычисление расстояния S (S 1 = T 1 P) два раза: из треугольников PA 1 T 1 и PA 2 T 2 и затем среднего из двух: (5. 27) - решение обратной геодезической задачи между пунктами T 1 и T 2 (вычисление α 12, L 1) и T 1 и T 3 (вычисление α 13, L 2), - вычисление углов μ 1 и μ 2 из треугольников PT 2 T 1 и PT 3 T 1: (5. 28)

(5. 29) - вычисление углов λ 1 и λ 2 из треугольников PT 2 T 1 и PT 3 T 1: - вычисление дирекционного угла линии T 1 P: (5. 30) - решение прямой геодезической задачи из пункта T на пункт P: (5. 31)

Привязка линейно-углового хода к стенным маркам. Стенные марки закладываются в цокольный этаж или в стену капитального здания; конструкции их бывают различными. Закладка стенных марок и определение их координат выполняется при создании геодезических сетей на территории населенных пунктов и промышленных предприятий; в дальнейшем эти марки играют роль опорных пунктов в последующих геодезических построениях. Привязка линейно-углового хода может быть выполнена к двум, трем или более стенным маркам. Схема привязки хода к двум маркам A и B показана на рис. 20. На линии AB с помощью рулетки измеряется отрезок S, и координаты точки P находятся из решения прямой геодезической задачи по формулам:

(5. 32) где α - дирекционный угол направления AB. а б б Рис. 20. Схема привязки хода: а - к двум маркам A и B; б – к трем маркам A, B и C С помощью рулетки измеряются расстояния S 1, S 2, S 3 и решается многократная линейная засечка; для большей надежности можно измерить углы β 1 и β 2 и решить комбинированную засечку.

В качестве примычного направления с известным дирекционным углом можно использовать либо направление на одну из стенных марок, либо направление на какой-нибудь другой пункт с известными координатами. Кроме метода засечек привязке ходов к стенным маркам применяют также полярный метод и метод редуцирования.

5. 2. 5. Понятие о системе линейноугловых ходов Совокупность линейно-угловых ходов, имеющих общие точки, называют системой ходов; узловой точкой называется точка, в которой сходятся не менее трех ходов. Как и для отдельного линейно - углового хода, для системы ходов применяют строгую и упрощенную обработку измерений. Упрощенную обработку рассмотрим на примере системы из трех линейноугловых ходов с одной узловой точкой (рис. 21). Каждый ход опирается на исходный пункт с известными координатами; на каждом исходном пункте имеется направление с известным дирекционным углом.

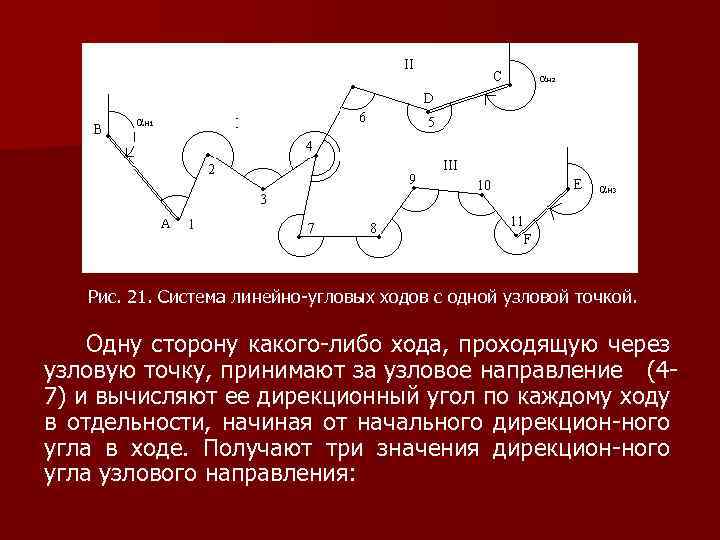Рис. 21. Система линейно-угловых ходов с одной узловой точкой. Одну сторону какого-либо хода, проходящую через узловую точку, принимают за узловое направление (47) и вычисляют ее дирекционный угол по каждому ходу в отдельности, начиная от начального дирекцион-ного угла в ходе. Получают три значения дирекцион-ного угла узлового направления:

α 1 - из первого хода, α 2 - из второго хода, α 3 - из третьего хода, и вычисляют средневесовое значение из трех, причем за вес отдельного значения принимают число 1/ni , где ni - количество углов в ходе от исходного направления до узлового направления (на рис. 21 n 1 = 4, n 2 = 3, n 3 = 5): (5. 33) Считая узловое направление исходным, т. е. имеющим известный дирекционный угол, вычисляют угловые невязки в каждом ходе по отдельности и вводят поправки в измеренные углы.

По исправленным углам вычисляют дирекционные углы всех сторон каждого хода и затем - приращения координат по всем сторонам ходов. По приращениям координат вычисляют координаты узловой точки по каждому ходу в отдельности и получают три значения координаты X и три значения координаты Y узловой точки. Средневесовые значения координат подсчитывают по формулам: (5. 34) (5. 35)

Считая узловую точку исходным пунктом с известными координатами, вычисляют координатные невязки для каждого хода в отдельности и вводят поправки в приращения координат по сторонам ходов. По исправленным приращениям координат вычисляют координаты пунктов всех ходов. Упрощенная обработка системы линейно - угловых ходов с одной узловой точкой состоит из двух этапов: получение дирекционного угла узлового направления и координат узловой точки и обработка каждого хода в отдельности.

6. Полигонометрия 6. 1. Принцип построения государственной геодезической сети При создании ГГС возникают три вопроса, имеющие принципиальное значение: - выбор схемы построения государственной геодезической сети на всей территории страны; - установление плотности геодезических пунктов; - установление точности определения взаимного положения смежных пунктов в сети. Каждый из этих вопросов необходимо рассматривать совместно, причем с двух точек зрения:

- решения основных научных задач геодезии; - решения задач картографирования территории страны. ГГС создают поэтапно, соблюдая принцип перехо-да от общего к частному. Сначала строят главную, состоящую из крупных геодезических построений в виде либо замкнутых полигонов. Измерения выполняют с наивысшей точностью. Затем данную сеть принимают за исходную и строят геодезическую сеть второго порядка с более детальными геометрическими построениями и с меньшей относительной точностью измерений. С теми же величинами абсолютных ошибок определения взаимного положения смежных пунктов, как и в сети первого порядка.

6. 2. Общие сведения о полигонометрии Полигонометрия - построение на местности системы ломаных линий, в которой измерены все отрезки линий s (рис. 22) и горизонтальные углы β между отрезками. Ломаную линию называют ходом , отрезок s – стороной или линией , горизонтальный угол между отрезками – углом поворота. Вершины полигонометрических ходов называют пунктами полигонометрии.

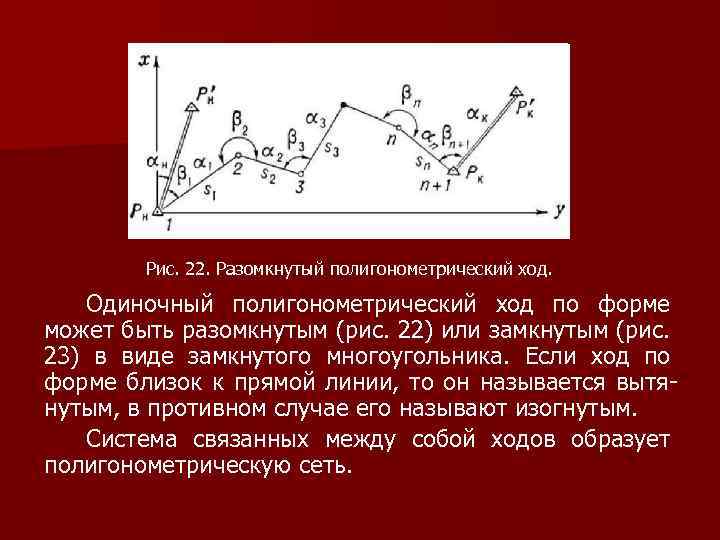Рис. 22. Разомкнутый полигонометрический ход. Одиночный полигонометрический ход по форме может быть разомкнутым (рис. 22) или замкнутым (рис. 23) в виде замкнутого многоугольника. Если ход по форме близок к прямой линии, то он называется вытянутым, в противном случае его называют изогнутым. Система связанных между собой ходов образует полигонометрическую сеть.

Рис. 23. Замкнутый полигонометрический ход. Отдельный ход между двумя узловыми пунктами или между исходным пунктом и узловой точкой называют звеном. Пункты геодезических сетей на местности закрепляют подземными сооружениями - центрами.

Ходы полигонометрии 1 класса прокладывают взамен рядов триангуляции 1 класса. Они строятся в виде полигонов, располагаемых примерно по меридианам и параллелям, с периметром около 800 км. Ходы полигонометрии 1 класса должны быть вытянутыми по форме и состоять не более чем из 10 сторон длиной 20 -25 км. Построение государственной геодезической сети 2 класса методом полигонометрии производится в каждом отдельном случае по особо разрабатываемой программе.

Точность измерений углов и линий в полигонометрии 2 класса должна быть в соответствии с величинами, указанными в табл. 1. При построении геодезических сетей 3 и 4 классов методом полигонометрии определение пунктов производится продолжением одиночных ходов или сетей, опирающихся на пункты высшего класса.

Каждое звено сети должно содержать не более двух точек поворота. Минимальная длина сторон в 3 классе - 3 км, в 4 классе - 2 км. Периметр полигонов не должен превос-ходить в 3 классе 60 км, в 4 классе - 35 км. Углы и линии измеряются с точностью, указанной в табл. 1. Полигонометрические сети часто создаются для обоснования крупномасштабных съе-мок, проводимых для специальных целей и для различного рода инженерных работ, свя-занных с разбивкой сооружений. В этом случае полигонометрия 4 класса развивается по специальным требованиям.

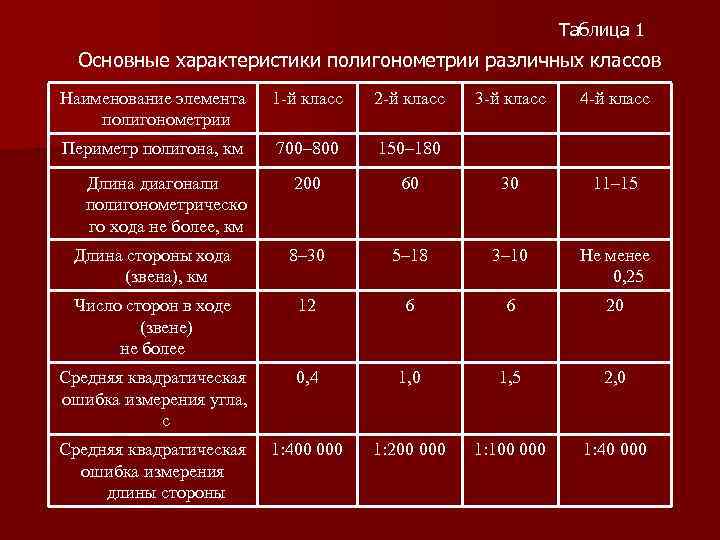Таблица 1 Основные характеристики полигонометрии различных классов Наименование элемента полигонометрии 1 -й класс 2 -й класс 3 -й класс 4 -й класс Периметр полигона, км 700– 800 150– 180 200 60 30 11– 15 Длина стороны хода (звена), км 8– 30 5– 18 3– 10 Не менее 0, 25 Число сторон в ходе (звене) не более 12 6 6 20 Средняя квадратическая ошибка измерения угла, с 0, 4 1, 0 1, 5 2, 0 Средняя квадратическая ошибка измерения длины стороны 1: 400 000 1: 200 000 1: 100 000 1: 40 000 Длина диагонали полигонометрическо го хода не более, км

Густота пунктов ГГС определяется Основными положениями о государственной геодезической сети Российской Федерации ГКИНП-01 -006 -03. Для съемок в масштабе 1: 25 000 и 1: 10 000 густота пунктов должна быть такой, чтобы на площадь в 50 - 60 км 2 приходился 1 пункт. Для обоснования топографических съемок масштабов 1: 5000, 1: 2000, 1: 1000 и 1: 500 необходимо иметь следующую плотность пунктов: - для съемок в масштабе 1: 5000 - 1 пункт на 20 - 30 км 2; - ≫ ≫ 1: 2000 и крупнее - 1 пункт на 5 - 15 км 2.

6. 3. Виды полигонометрии Определение положения геодезических пунктов методом полигонометрии сводится к прокладыванию на местности ходов, в которых производят измерения углов поворота и длин линий. Углы в полигонометрии измеряют оптическими теодолитами с точностью, предусмотренной для данного класса или разряда. Для измерения линий применяются различные методы: 1) светодальномерный, когда длину линии измеряют путем определения времени распространения света вдоль измеряемой линии; 2) радиодальномерный, основанный на том же принципе, но использующий распространение радиоволн;

3) непосредственный, при котором длины линий измеряются откладыванием мерного прибора вдоль измеряемой линии; 4) дальномерный, когда длины линий измеряют различными типами оптико-механических дальномеров; 5) короткобазисный параллактический, при котором длину линии определяют от короткого базиса через вспомогательную геометрическую фигуру с измеренными углами. Точность указанных методов линейных измерений неодинакова, поэтому и применяются они соответственно в разных классах и разрядах полигонометрии.

Различаются следующие виды полигонометрии: - светодальномерная; - радиодальномерная; - с непосредственным измерением линий; - дальномерная; - короткобазисная параллактическая. Светодальномерная и радиодальномерная полигонометрия применяется при развитии геодезических сетей всех классов и разрядов, а также и специальных геодезических сетей. Полигонометрия с непосредственным измерением линий применяется в тех случаях, когда линии имеют небольшую длину. Дальномерная полигонометрия применяется для определения положения пунктов 2 разряда, так как точность измерения расстояний оптическими дальномерами относительно невелика.

Короткобазисная параллактическая полигонометрия применяется при проложении полигонометрических ходов и сетей 1 и 2 разрядов. Отдельные параллактические звенья могут строиться на местности и при непосредственном измерении сторон. 6. 4. Требования, предъявляемые к полигонометрии 4 класса, 1 и 2 разрядов Полигонометрия 4 класса, 1 и 2 разрядов создается в виде отдельных ходов или сетей. Полигонометрические сети должны содержать избыточное число исходных данных. Основные показатели полигонометрии 4 класса, 1 и 2 разрядов приведены в табл. 2.

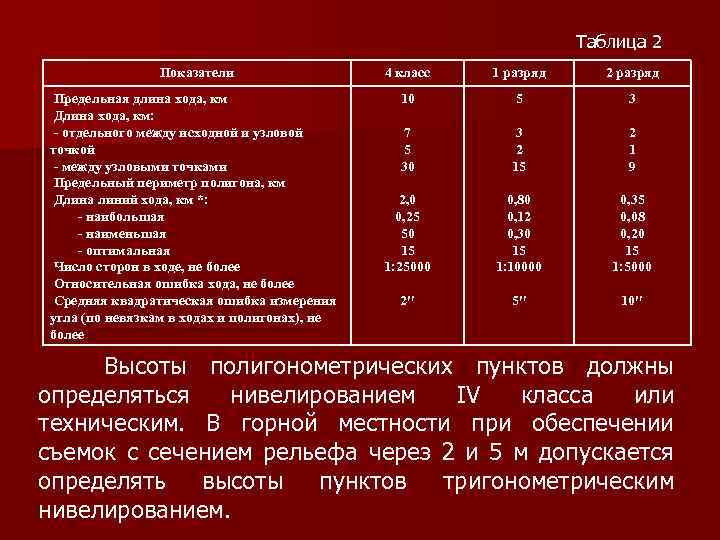Таблица 2 Показатели 4 класс 1 разряд 2 разряд Предельная длина хода, км Длина хода, км: - отдельного между исходной и узловой точкой - между узловыми точками Предельный периметр полигона, км Длина линий хода, км *: - наибольшая - наименьшая - оптимальная Число сторон в ходе, не более Относительная ошибка хода, не более Средняя квадратическая ошибка измерения угла (по невязкам в ходах и полигонах), не более 10 5 3 7 5 30 3 2 15 2 1 9 2, 0 0, 25 50 15 1: 25000 0, 80 0, 12 0, 30 15 1: 10000 0, 35 0, 08 0, 20 15 1: 5000 2″ 5″ 10″ Высоты полигонометрических пунктов должны определяться нивелированием IV класса или техническим. В горной местности при обеспечении съемок с сечением рельефа через 2 и 5 м допускается определять высоты пунктов тригонометрическим нивелированием.

6. 5. Действие ошибок угловых и линейных измерений Допустим, что между двумя пунктами Pн и Pк проложен полигонометрический ход (рис. 1), в котором измерены все n сторон и все (n + 1). левых (или правых) углов. Вследствие измерения углы будут ошибочны на величины dβ 1, dβ 2, . . . , dβ(n+1) и стороны - на величины ds 1, ds 2, . . . , dsn. Исходные дирекционные углы αн, αк и исходные координаты хн, ун и хк, ук известны. Тогда в полигонометрическом ходе измеренные значения углов вместе с исходными данными позволяют вычислить невязку в углах fβ.

(6. 1) Из формулы (6. 1) по правилам теории ошибок получим или, предполагая, что углы были измерены равноточно, (6. 2) Так как при измерении углов имеют место источники ошибок как случайного, так и систематического характера, то каждая ошибка dβ будет состоять из случайной Δβ и систематической σβ частей: dβ = Δβ + σβ,

тогда и средняя квадратическая ошибка угла β согласно теории ошибок будет также включать в себя систематическую и случайную части: (6. 3) Если считать, что дирекционные углы αн, αк также имеют ошибки, то по (6. 1) с учетом выражения (6. 2) пред f = пред d можно найти β β (6. 4) От средней квадратической ошибки суммы углов по формуле (6. 2) перейдем к предельной, которая является ни чем иным, как невязкой пред fβ = пред dβ (6. 5)

Полагая, что пред dβ = 2 тβ, запишем пред fβ = пред 2 тβ (6. 6) Линейная ошибка хода. Для простоты рассуждений положим, что полигонометрический ход имеет вытянутую форму (рис. 24). Для такого хода можно написать αн αк β 1 β 2 β 3 βn-1 βn βn+1 t Tк Tн L L Рис. 24. Вытянутый ход полигонометрии u mu mt M u P'n+1

L = S 1+ S 2 + …+ Sn = [S], (6. 7) где L - расстояние между крайними пунктами Тн и Тк - замыкающая хода. Ошибка измерения всех линий d. L в вытянутом ходе в результате ошибок, допущенных в каждой линии dsi согласно (6. 7) будет d. L = ds 1 + ds 2 + … + dsn. (6. 8) Переходя к средним квадратическим ошибкам, получим (6. 9) Так как при измерении линии действуют источники ошибок случайного и систематического характера и ошибка каждой линии dsi состоит из случайной Δ и систематической σ частей

dsi = Δsi + σsi , где i = 1, 2, . . . , n, то (6. 10) Структура величин mΔ и тσ будет зависеть от метода измерения линий. При измерении линий, например, светодальномером и инварной проволокой она будет совершенно разной. Если при измерении линий отсутствуют систематические ошибки, т. е. σsi = 0, то (6. 11)

Систематическим влиянием можно пренебречь и в том случае, если средняя квадратическая систематическая ошибка по своей величине не превышает 1/3 средней квадратической случайной ошибки. Действительно, если принять (6. 12) то (6. 13) т. е. значение ms, если пренебречь систематической ошибкой, уменьшится на 5%. При

значение ms уменьшится на 2%, следовательно, в этом случае также можно считать, что 6. 6. Продольная и поперечная ошибки 6. 6. полигонометрического хода В полигонометрическом ходе любой формы невязки fx и fy в приращениях координат определяют по известным формулам (6. 14)

Абсолютная линейная невязка fs в периметре хода будет равна (6. 15) Разложим в периметре невязку fs на два компонента, обозначив их через t и и. Компонент t расположен вдоль хода по направлению замыкающей L, а u – перпендикулярно к ней. Продольный компонент t, который называют продольной невязкой, является следствием накопления ошибок линейных измерений, а поперечный компонент и - поперечная невязка - следствием накопления ошибок измерения углов. Тогда (6. 16)

Ошибки измерения линий d. L = Σds составят величину продольной невязки t = d. L , средняя квадратическая величина которой согласно (6. 9) будет равна (6. 17) Установим связь между поперечной невязкой и ошибками в углах. Если в первом угле имела место ошибка (рис. 25), то при безошибочности всех остальных углов последняя точка хода Рn+1 переместится перпендикулярно к направлению хода на величину Δu‘ 1 под влиянием ошибки dβ 2, допущенной во втором угле, точка Рn+1 сместится на величину Δи‘ 2 и т. д. и под влиянием ошибки в угле βn смещение точки выразится через Δи‘n. Следовательно, для смещений имеем

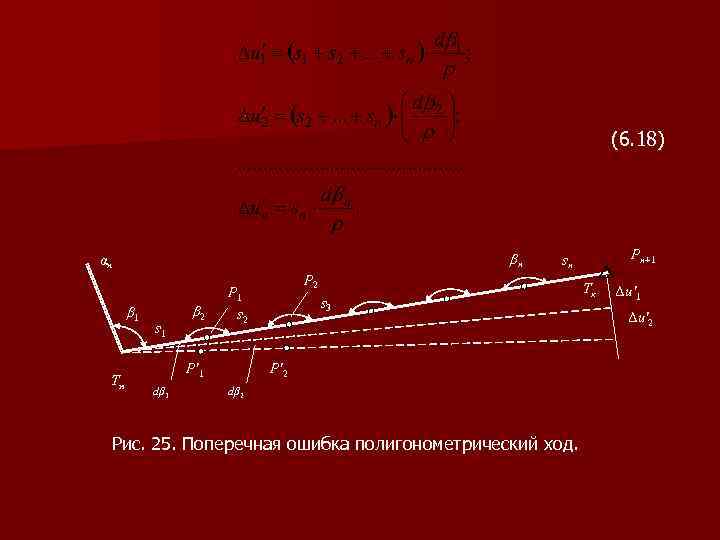(6. 18) βn αн β 1 Tн s 1 β 2 P'1 dβ 1 P 2 P 1 s 2 Pn+1 sn s 3 P'2 dβ 2 Рис. 25. Поперечная ошибка полигонометрический ход. Tк Δu'1 Δu'2

Суммируя отдельные смещения конечной точки хода, получим поперечную невязку и' (6. 19) Следовательно, с учетом (6. 18), и предположив для простоты расчета, что все стороны хода примерно одинаковы, тогда (6. 20) Переходя к средним квадратическим ошибкам, получим для среднего квадратического значения поперечной невязки (поперечного сдвига конечной точки хода)

(6. 21) Но и мы будем иметь (6. 22) Преобразуем полученное выражение. Умножим числитель и знаменатель правой части на n и положим s∙n = L, тогда формуле (6. 22) можно придать вид (6. 23)

Или с учетом упрощений (6. 24) Средняя квадратическая поперечная невязка хода зависит от длины хода, количества линий в нем и точности измерения углов.

6. 7. Средняя квадатическая ошибка положения конечной точки хода 1. Ход вытянутый, углы предварительно не уравнены (рис. 24). Найдем среднюю квадратическую величину самого вектора М, которая будет называться средней квадратической ошибкой положения конечной точки полигонометрического хода, (6. 25) Принимая во внимание выражения (6. 17) и (6. 24), будем иметь (6. 26)

Средняя квадратическая ошибка положения конечной точки вытянутого висячего полигонометрического хода зависит от точности измерения линий и углов в ходе, длины хода и количества линий в нем. 2. Ход изогнутый, углы предварительно не исправлены. В ходе изогнутой формы будут иметь место невязки f'x и f'y , и невязка в периметре выразится формулой (6. 15). Предположим, что для одного и того же хода k раз измерены все углы и все линии. В соответствии с этим можно найти k значений для невязок f'x и f'y , а следовательно, и k значений для неневязки f's в периметре. В результате будем иметь k равенств где i = 1 , 2, . . . , k.

Складывая все равенства почленно и деля левую и правую части на k , получим, что каждый член равенства представляет собой соответствующее среднее квадратическое значение (6. 27) Для установления связи величины М ' со средними квадратическими ошибками измерения линий ms и углов тβ воспользуемся без вывода так называемыми координатными условными уравнениями. (6. 28)

где αi - дирекционный угол линий хода; v. S и vβ – соответственно поправки в измеренные значения линий и углов; хn+1 - х и yn+1 - yi - разности координат между конечной и каждой точкой хода; f'x и f'y - невязки в приращениях координат. Перенесем f'x и f'y в правую часть в часть, и учитывая, что (6. 29) можно записать (6. 30)

Переходя по правилам теории ошибок к средним квадратическим ошибкам, будем иметь (6. 31) Средняя квадратическая ошибка в положении конечной точки хода М' по формуле (6. 27) будет равна (6. 32) Обозначим (6. 33)

И с учетом (6. 33) можно записать (6. 34) Средняя квадратическая ошибка положения конечной точки висячего изогнутого полигонометрического хода зависит не только от ошибок измерений, но и от степени изогнутости хода и количества углов поворота в нем. Величина [D 2 n+1, i] будет тем меньше, чем больше изогнут ход и чем меньше в нем углов поворота. В действительности исходные данные (координаты и дирекционные углы) сами содержат ошибки и поэтому между указанными выше величинами невязки и ошибки будет некоторая разница.

Формула средней квадратической ошибки в положении конечной точки хода в этом случае будет учитывать и ошибки полевых измерений, и ошибки исходных данных (6. 35) где тαн - средняя квадратическая ошибка дирекцион- ного угла αн; m(н-к) - средняя квадратическая ошибка конечного пункта Тк по отношению к пункту Тн. В строго вытянутом ходе с равными сторонами дирекционные углы всех линий одинаковы и равны дирекционному углу направления всего хода α.

Для такого хода формула (6. 35) преобразуется в следующий вид (6. 36) 3. Ход изогнутый (рис. 26), углы предварительно исправлены за невязку. Координатные условные уравнения для полигонометрического хода, в котором измеренные углы были предварительно исправлены поправками, вычисляемыми по формуле записываются так:

Рис. 26. Изогнутый полигонометрический ход (6. 37) здесь η и ξ - центральные координаты (ордината и абсцисса), полученные относительно системы координат, начало которой находится в центре тяжести хода;

v" - вторичные поправки в измеренные углы. Координаты X 0 и Y 0 центра тяжести хода определяют по формулам (6. 38) центральные координаты — по формулам (6. 39) Так как η и ξ, вычисляемые по формулам (6. 39), представляют собой уклонения от средних арифметических, которыми являются X 0 и Y 0, то, следовательно

(6. 40) В формулах (6. 37) вторичные поправки в углы vβ" величины зависимые, так как они входят составной частью в общие поправки в углы vβ. Следовательно, vβ" определится согласно (6. 41) и подставим в (6. 37). Тогда получим (6. 42)

Третьи члены уравнений (6. 42) будут равны нулю, так как первичная поправка v'β - величина одинаковая для всех углов; она может быть вынесена за знак суммы, тогда суммы центральных координат по формулам (6. 40) будут равны нулю. С учетом этого уравнения (6. 42) примут вид (6. 43) Перенесем в уравнениях (6. 43) fx и fy в правую часть и по аналогии с действиями в случае висячего хода заменим поправки vs и vβ на истинные ошибки ds, dp согласно формулам (6. 29)

Переходя к средним квадратическим ошибкам (учитывая при этом, что углы в ходе измерены равноточно), будем иметь (6. 44) Средняя квадратическая ошибка положения конечной точки хода согласно формуле (6. 27) равна сумме величин тx и ту, следовательно, (6. 45)

Обозначим (6. 46) Здесь D 0, i есть расстояния между центром тяжести вершин хода и каждым его пунктом (рис. 27). С учетом (6. 46) формулу (6. 45) можно записать (6. 47) Рис. 27. Схема определения расстояний от центра тяжести до точек

т. е. средняя квадратическая ошибка положения конечной точки полигонометрического хода при исправленных за невязку углах зависит от ошибок измерений, степени изогнутости хода и количества углов поворота в нем. Величина [D 20, i] будет тем меньше, чем меньше изломан ход и чем меньше в нем углов поворота. Сравнивая полученную формулу с формулой (6. 34), видим, что одна формула отличается от другой последним членом в правой части. Если в исходных данных хода имели место ошибки, то формула (6. 47) получит несколько иной вид; в этом случае (6. 48) где D 1, 0 > Dn+1, 0 - соответственно расстояния от центра тяжести до начальной и конечной точек хода;

тα - средняя квадратическая ошибка начального и конечного дирекционных углов; m н-к- средняя квадратическая ошибка конечного пункта Тк по отношению к пункту Tн. 4. Ход вытянутый, углы предварительно исправлены за невязку. Положим, что вытянутый ход имеет n равных линий s, причем n - число четное, тогда центр тяжести хода будет лежать в его середине. Величину [D 20, i ] для такого хода можно представить выражением (рис. 28) или

Сумма в фигурных скобках есть сумма квадратов чисел натуральног ряда, которая равна Тогда (6. 49) Умножим числитель и знаменатель на n и, учитывая, что s 2 n 2 = L 2, получим Рис. 28

Разделив теперь в полученном выражении каждый член в числителе и знаменателе на n и отбросив по малости величину 2/n, найдем (6. 50) С учетом выражения (6. 50) формула для средней квадратической ошибки положения конечной точки вытянутого полигонометрического хода будет иметь вид (6. 51) При наличии ошибок в исходных дирекционных углах и координатах формула (6. 51) будет иметь вид

(6. 52) Сравнение формул (6. 36) и (6. 52) показывает, что предварительное исправление углов уменьшает влияние ошибок исходных дирекционных углов на невязку в периметре в раз. 5. Ход замкнутый, углы предварительно не исправлены за невязку. Если конечная точка Тк совпадает с точкой Тн, то ход из разомкнутого превращается в замкнутый, но выведенные формулы для разомкнутого хода остаются в силе и в данном случае. Для разомкнутого хода формула (6. 34) может быть представлена в виде (6. 53)

Как видно, при прочих равных условиях в замкнутом ходе надо ожидать среднюю квадратическую ошибку меньше, чем в соответствующем по периметру, числу углов поворота и точности угловых и линейных измерений разомкнутом ходе, особенно, если последний вытянутый. В замкнутом ходе ошибки начального дирекционного угла и координат начального пункта не оказывают никакого влияния на величину невязки в периметре, а следовательно, и на величину М‘. 6. Ход замкнутый, углы предварительно исправлены за невязку. Формула (6. 47) полностью применима и для замкнутого хода (рис. 23), только при подсчете величин [ξ 2], [η 2] и [D 20, i] точка Тн будет участвовать дважды. Примем приближенно замкнутый ход по форме за правильный многоугольник с равными сторонами. При n большом периметр многоугольника будет приближаться к длине окружности.

Можно положить, что D 1 ≈ R, тогда Откуда Следовательно, (6. 54) С учетом выражения (6. 54), в котором π ≈ 10, формула (6. 47) примет вид (6. 55)

Из полученной формулы можно прийти к заключению, что и после предварительного исправления выводы, сделанные относительно величины средней квадратической ошибки замкнутого хода с углами, не исправленными за невязку, остаются в силе и в этом случае. 7. Азимутальный ход. Для полигонометрического хода любой формы с независимым определением дирекционного угла каждой линии, например из гиротеодолитных измерений, координатные условные уравнения записываются так: (6. 56)

Учитывая вывод средней квадратической ошибки положения конечной точки изогнутого полигонометрического хода с измеренными углами поворота к ходу с измеренными дирекционными углами, нетрудно получить для mx 2, my 2 и М 2 следующие выражения: При наличии заметных ошибок в исходных координатах формула (V III. 63) запишется в виде (6. 57) (6. 58) При наличии заметных ошибок в исходных координатах формула (6. 58) запишется в виде

(6. 59) Для ходов вытянутой формы с примерно равными линиями формулы (6. 58) и (6. 59) примут более простой вид: (6. 60) (6. 61)

6. 8. Ослабление влияния угловых и линейных ошибок Для уменьшения влияния ошибки угловых измерений на поперечную невязку, а значит и на общий сдвиг конечной точки хода можно определить азимут, а затем и дирекционный угол некоторых линий хода путем астрономических или гиротеодолитных измерений, например Рi , Рn+1(рис. 29, а) или Pi. N (рис. 29, б). При этом в последнем случае одновременно измеряют примычные углы βк 1 и βк 2 для передачи дирекционного угла на стороны хода, сходящиеся в точке Pi (рис. 29, б).

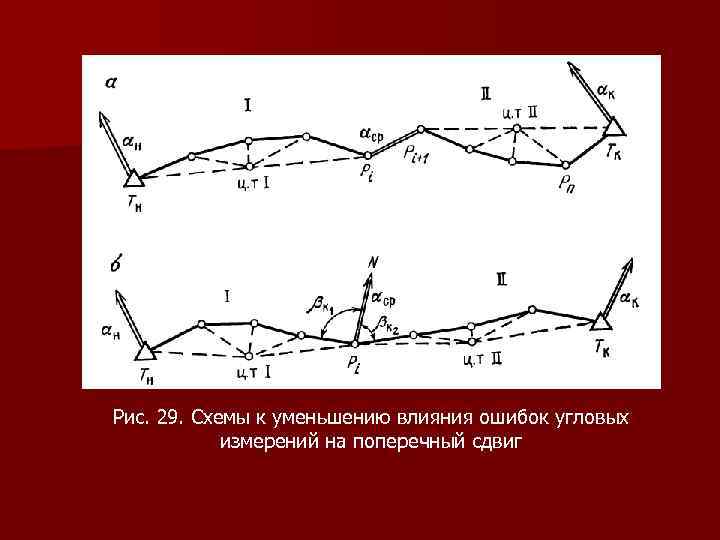Рис. 29. Схемы к уменьшению влияния ошибок угловых измерений на поперечный сдвиг

Наличие промежуточного дирекционного угла разбивает весь ход на две секции I и II и дает возможность вычислить невязки для каждой секции и увязать углы каждой секции отдельно. Для такого хода координатные условные уравнения записываются так: (6. 62) Следовательно (6. 63)

Откуда, переходя к средним квадратическим ошибкам, имеем (6. 64) Суммирование квадратов ошибок дает (6. 65) С учетом формулы (6. 46) (6. 66)

Тогда формула (6. 65) примет вид: (6. 67) где [D 02, i]I , [D 0, 2 i ]II - суммы квадратов расстояний от центра тяжести каждой секции до точек хода, входящих в секцию (рис. 29, а, б). Из рис. 29 видно, что в ходе с промежуточным дирекционным углом выражение {[D 02, i]I+ [D 0, 2 i ]II} в том же ходе без промежуточного дирекционного угла, а следовательно, будет меньше величина М - и точность хода повысится. При числе секций в ходе, равном к, выражение в фигурных скобках формулы (6. 67) будет представлять сумму величин [D 02, i] от 1 секции до kй.

Если ход будет иметь вытянутую форму и линии в ходе будут равны между собой, то (6. 68) При числе линий n правую часть выражения (6. 68) можно представить или после преобразований (6. 69)

С учетом (6. 69) формула средней квадратической ошибки положения конечной точки вытянутого полигонометрического хода с промежуточными дирекционными углами будет иметь вид: (6. 70) При числе сторон n = 16 и k = 2 при прочих равных условиях второй член в формуле (6. 70) будет меньше по сравнению с формулой (6. 51) в три раза. Ослабить влияние ошибок линейных измерений можно следующим образом: 1) увеличить точность измерений линий хода; 2) уменьшить длину хода между двумя исходными пунктами; 3) придать ходу прямолинейную форму.

6. 9. Критерий степени изогнутости хода Проложить на местности ход, в котором все углы поворота равнялись бы точно 180 o, невозможно. Поэтому полигонометрический ход может считаться вытянутым лишь с некоторым приближением. Установим предел, в котором можно считать ход вытянутым, или критерий степени изогнутости полигонометрического хода, который необходим при расчетах точности ходов при их проектировании, и при оценке точности и уравнивании ходов, проложенных на местности. В ходах вытянутой формы продольная невязка является результатом только линейных ошибок, а поперечная - только угловых.

Если ход лишь немного отклоняется по форме от прямолинейной, то влияние угловых ошибок на продольный сдвиг и линейных на поперечный будет невелико. n Получим продольную и поперечную средние квадратические ошибки и для изогнутого хода. Повернем оси координат (рис. 30) с началом в центре тяжести хода на величину дирекционного угла Θ замыкающей хода L и разложим невязку в периметре fs на компоненты вдоль замыкающей - продольную невязку t и перпендикулярно к ней - поперечную невязку и. Обозначим координаты точек хода Pi [i = 1, 2, . . . , (n + 1)] при новом положении через ξ‘i и η‘i , а дирекционные углы линий хода s‘I (i = 1, 2, … , n) – через αi

Рис. 30. Схема к определению продольной и поперечной средних квадратических ошибок Тогда для хода с исправленными углами по аналогии c формулой (6. 44) можно написать

(6. 71) (6. 72) Ход можно будет считать вытянутым, если в формуле (6. 71) второй, а в формуле (6. 72) первый члены будут очень незначительными и могут быть отброшены, т. е. (6. 73)

Если один из двух источников ошибок характеризуется средней квадратической ошибкой, не превышающей 1/k средней квадратической ошибки, характеризующей другой источник ошибок, то первым можно пренебречь. На основании этого (6. 74) Согласно принципу равных влияний (6. 75)

можно написать при достаточной вытянутости хода или (6. 76) Введем в выражение (6. 76) среднюю величину (6. 77) о учетом которой будем иметь (6. 78)

Или (6. 80) Из второго уравнения (6. 72) согласно принципу равных влияний напишем При принятых равных линиях s величины m. S также будут равными, поэтому в выражении (6. 80) их можно вынести за знак суммы и сократить. (6. 81)

Введем средние величины (6. 82) с учетом выражений (6. 82) равенству (6. 81) можно придать вид (6. 83) Отсюда (6. 84)

При k = 7 для выражений (6. 80) и (6. 84) будем иметь откуда α 0' ≈ 8°. Для предельного значения согласно правилам теории ошибок находим (6. 85) Следовательно, ход можно считать достаточно вытянутым, если точки хода отклоняются в обе стороны от линии, проведенной через центр тяжести параллельно замыкающей хода, в среднем на величину 1/24 (в пределе на 1/8) длины самой замыкающей и линии хода отклоняются от направле-ния замыкающей в обе стороны на 8° (в пределе на 24°).

В качестве критерия степени изогнутости хода иногда употребляется еще отношение [s]/L. Величина дроби [s]/L будет зависеть от формы хода: чем искривленнее ход, тем эта дробь будет больше. Ход считается достаточно вытянутым, если (6. 86) 6. 10. Организация работ. Составление проекта. Полигонометрические работы состоят из следующих процессов: 1) составление проекта; 2) рекогносцировка трассы и пунктов полигонометрического хода; 3) установка знаков и закладка центров; 4) измерение углов; 5) измерение линий; 6) привязка к пунктам госу-

дарственной геодезической сети высших классов и разрядов; 7) обработка результатов полевых измерений; 8) предварительные вычисления и оценка точности полевых измерений; 9) уравнительные вычисления и оценка точности полученных результатов; 10) составление каталога; 11) составление технического отчета. Проектирование полигонометрических ходов и сетей 4 класса, 1 и 2 разрядов производят с учетом масштаба и метода предстоящих съемок, требова-ний Инструкции, а также и специальных требо-ваний, предъявляемых проектными и другими организациями. До начала проектирования необходимо определить границы обеспечиваемого района; собрать данные об условиях работ в нем.

Полигонометрические ходы проектируют в виде отдельных разомкнутых ходов, опирающихся на два исходных пункта. При обеспечении геодезическими пунктами значительных площадей проектируют полигонометрические сети. При этом следует учитывать, что ходы и сети 4 класса должны опираться на пункты триангуляции и полигонометрии высших классов. Ходы и сети 1 разряда должны прокладываться между пунктами 4 класса, ходы и сети 2 разряда - между пунктами ходов 1 разряда. При составлении проекта вначале задаются наиболее целесообразной схемой построения сети, точностью измерения углов и линий.

Детальное проектирование полигонометрических ходов 4 класса, 1 и 2 разрядов для незастроенной территории производят на топографических картах масштаба 1: 25 000, а для застроенной территории - масштаба 1: 10 000. Ходы должны прокладываться по местности, наиболее благоприятной для производства угловых и линейных измерений. После того как намечено направление отдельных ходов, переходят к выбору положения отдельных пунктов с соблюдением максимальной и минимальной длины линий. После разработки проекта подсчитывают объем работ, определяют потребности в приборах, материалах, транспорте, техническом персонале и рабочей силе. На основе этого составляют смету затрат и план организации работ. Все эти документы затем уточняют на основании данных рекогносцировки.

6. 11. Расчет точности полигонометрических ходов При составлении проекта необходимо предвычис- лить ожидаемую точность каждого запроектированного на карте полигонометрического хода. Расчетную часть для каждого хода начинают с установления формы хода. Для этого используют критерии степени изогнутости, указанные в выражениях (6. 85), (6. 86). Рис. 31. Схема к определению отклонений линий хода от замыкающей

Как известно, точность запроектированного хода будет характеризоваться предельной ошибкой пункта в самом слабом месте хода после его уравнивания. В полигонометрическом ходе до уравнивания, как уже было установлено, самую большую ошибку будет иметь пункт, расположенный в конце хода. При привязке конца хода к исходному пункту наименьшей точностью после уравнивания координат будет обладать пункт, расположенный в середине хода, как наиболее удаленный от обоих исходных пунктов. Положение средней точки Е полигонометрического хода, проложенного между двумя исходными пунктами Тн и Тк длиной L, определяется по формуле арифметического среднего из двух равноточных результатов, вычисленных от концов хода.