Геодезия и топография Общие понятия и принципы

ЛИТЕРАТУРА 1. Господинов Г. В. , Сорокин В. Н. Топография. Изд-во МГУ, Москва, 1974 2. Киселев М. И. , Михелев Д. Ш. Основы геодезии. Изд-во «Высшая школа» , Москва, 2001, 368 с. 3. Куштин И. Ф. , Куштин В. И. Инженерная геодезия. Издво «Феникс» , Ростов-на-Дону, 2002, 416 с. 4. Харипко А. С. , Божок А. П. Топография с основами геодезии. М. : Высшая школа, 1986.

Геодезия Слово "геодезия" образовано из греческих слов (от греч. "гео" – Земля и греч. "дайдзо" – разделяю) Геодезия –наука, изучающая форму Земли в целом, ее временные изменения и разрабатывающая принципы измерения земной поверхности. Топография – наука, изучающая объективное состояние земной поверхности в аспекте расположения и характеристик находящихся на ней объектов. Картография – наука, изучающая методы и процессы создания и использования карт, планов, атласов и другой картографической продукции.

Основные задачи геодезии • - определение фигуры, размеров Земли и её гравитационного поля, • - распространение единой системы координат на территорию отдельного государства, континента и всей земли в целом, • - изображение участков поверхности земли на топографических картах и планах, • - изучение глобальных смещений блоков земной коры

Основные принципы геодезического проектирования. • - Два этапа • - Использование упрощенной поверхности для промежуточного проектирования Свойства упрощенной поверхности. - Стационарность • - Простота описания и высокая степень гладкости • - Близость к реальной поверхности Земли.

Основные этапы определения формы и размеров Земли 1. 2. 3. 4. с древнейших времен до конца XVII в. , когда Землю принимали за шар; с конца XVII в. до второй половины XIX в, когда считали, что Земля является сплюснутым у полюсов шаром, т. е. эллипсоидом вращения; со второй половины XIX в до сороковых годов XX в. , когда установили, что более правильно представлять Землю трехосным эллипсоидом; с сороковых годов XX в до настоящего времени, когда за фигуру Земли принимают тело, ограниченное физической поверхностью Земли.

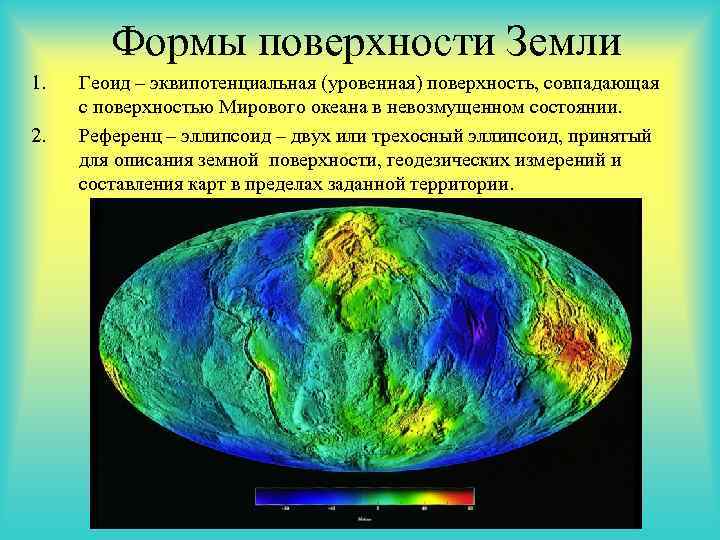
Формы поверхности Земли 1. 2. Геоид – эквипотенциальная (уровенная) поверхность, совпадающая с поверхностью Мирового океана в невозмущенном состоянии. Референц – эллипсоид – двух или трехосный эллипсоид, принятый для описания земной поверхности, геодезических измерений и составления карт в пределах заданной территории.

Уровенная поверхность Уровенной называют поверхность, в каждой точке которой потенциал силы тяжести имеет одинаковое значение.

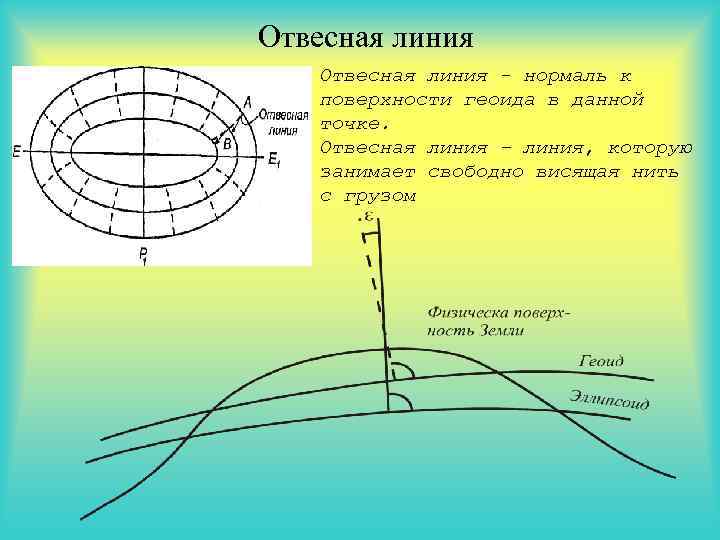
Отвесная линия - нормаль к поверхности геоида в данной точке. Отвесная линия – линия, которую занимает свободно висящая нить с грузом

Элементы и параметры эллипсоида 1. 2. 3. 4. 5. 6. Полюса – точки пересечения малой оси с поверхностью эллипсоида. Экватор – сечение поверхности плоскостью, проходящей через центр и перпендикулярной малой оси. Параллель – сечение поверхности плоскостью, перпендикулярной малой оси. Меридиан – сечение поверхности плоскостью, проходящей через малую ось. а, b – длина большой и малой полуоси = (a-b)/a – сжатие эллипсоида

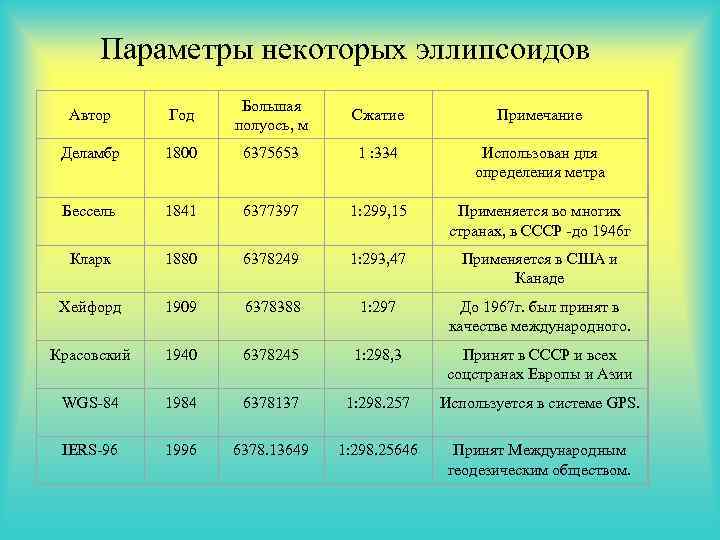
Параметры некоторых эллипсоидов Автор Большая полуось, м Сжатие Примечание Деламбр 1800 6375653 1 : 334 Использован для определения метра Бессель 1841 6377397 1: 299, 15 Применяется во многих странах, в СССР -до 1946 г Кларк 1880 6378249 1: 293, 47 Применяется в США и . Канаде Хейфорд 1909 6378388 1: 297 До 1967 г. был принят в качестве международного. Красовский 1940 6378245 1: 298, 3 Принят в СССР и всех соцстранах Европы и Азии WGS-84 1984 6378137 1: 298. 257 Используется в системе GPS. IERS-96 Год 1996 6378. 13649 1: 298. 25646 Принят Международным геодезическим обществом.

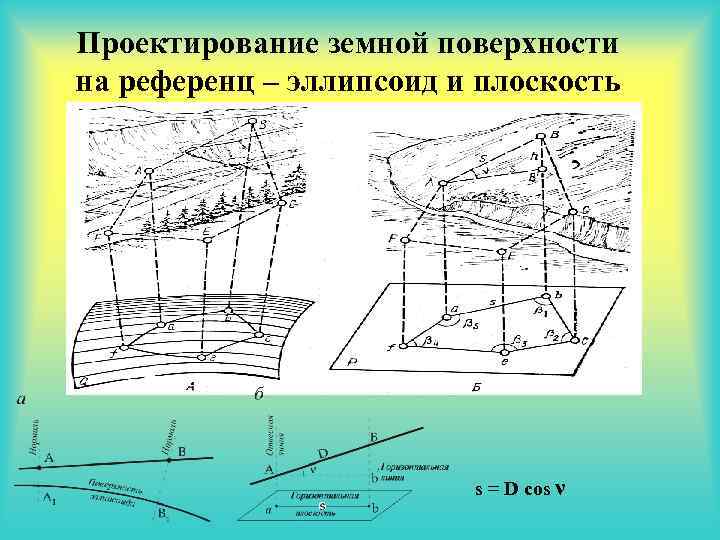
Проектирование земной поверхности на референц – эллипсоид и плоскость s = D cos ν

Cистемы координат Географические геодезические координаты Геодезической широтой В называют угол между нормалью к поверхности эллипсоида в данной точке и плоскостью геодезического экватора. Геодезической долготой L, называют двугранный угол между плоскостью начального геодезического меридиана и плоскостью геодезического меридиана, проходящего через данную точку. Геодезической высотой Н называют расстояние от данной точки до поверхности эллипсоида по нормали к ней.

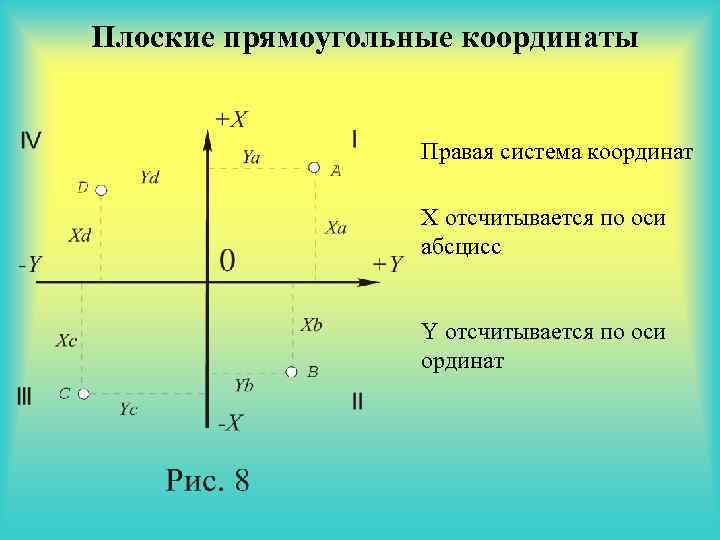
Плоские прямоугольные координаты Правая система координат X отсчитывается по оси абсцисс Y отсчитывается по оси ординат

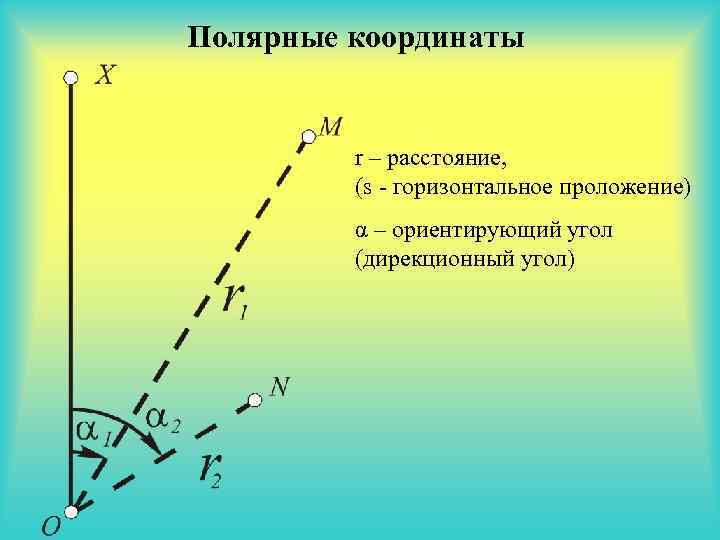
Полярные координаты r – расстояние, (s - горизонтальное проложение) α – ориентирующий угол (дирекционный угол)

Прямая геодезическая задача состоит в определении координат конечной точки линии по длине ее горизонтального проложения, направлению и координатам начальной точки XB = XA + ΔXAB YB = YA + ΔYAB XAB = S cos α, YAB = S sin α XB = XA + S cos α, YB = YA + S sin α

Обратная геодезическая задача S = √(хв-ха)2 + (ув-уа)2

Масштаб – отношение длины линии на карте (l) к соответствующему ей горизонтальному проложению на местности (s). l: s Повышение отношения l : s означает переход к более крупному масштабу. Тип карты Мелкомасштабная Среднемасштабная Крупномасштабная План Масштаб 1: 1000000, 1: 500000 1: 300000, 1: 200000, 1: 100000 1: 50000, 1: 25000, 1: 10000 1: 5000, 1: 2000, 1: 1000, 1: 500

Картографическая проекция Гаусса Lw = 6 o(n-1) Lc = 6 on - 3 o Lo = 6 on 1: 50000 – ΔS/S = 1/1700 1: 10000 – ΔS/S = 1/800 Lw = 3 on – 1. 5 o Lc = 3 on Lo = 3 on + 1. 5 o 1: 50000 – ΔS/S = 1/6800 1: 10000 – ΔS/S = 1/3100

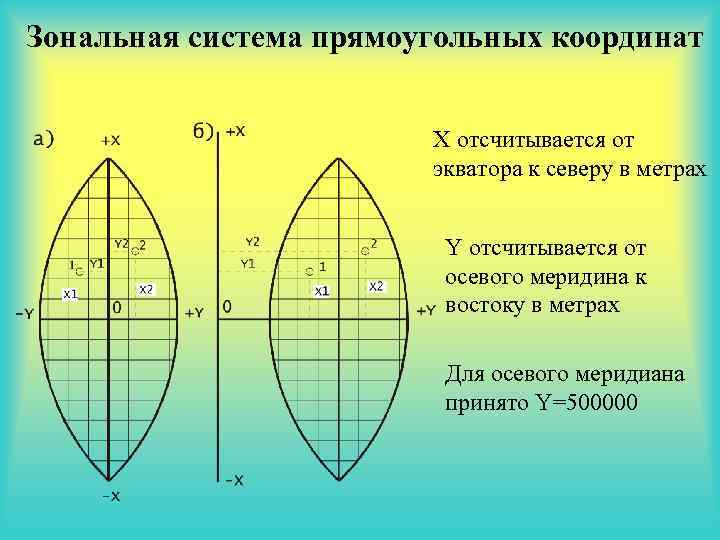
Зональная система прямоугольных координат X отсчитывается от экватора к северу в метрах Y отсчитывается от осевого меридина к востоку в метрах Для осевого меридиана принято Y=500000

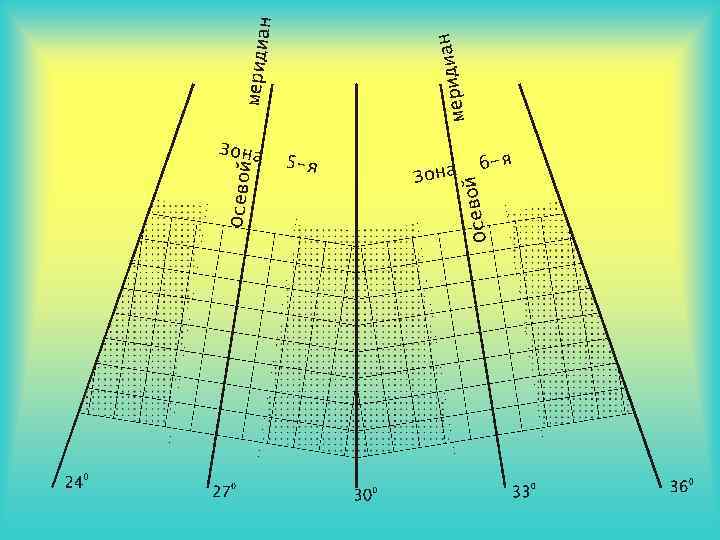
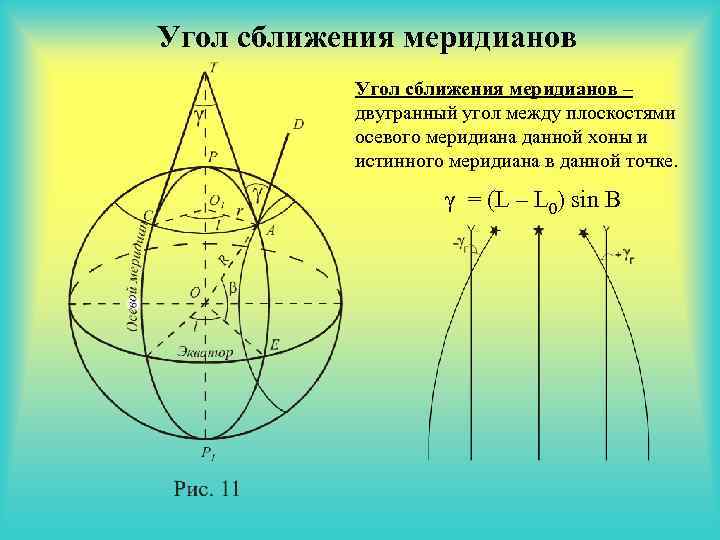
Угол сближения меридианов – двугранный угол между плоскостями осевого меридиана данной хоны и истинного меридиана в данной точке. γ = (L – L 0) sin B

Ориентирующие углы направлений Дирекционный угол (α) – двугранный плоскостью осевого меридиана и плоскостью, проходящей через заданное направление и центр Земли. Азимут (A)– двугранный плоскостью истинного меридиана и плоскостью, проходящей через заданное направление и центр Земли. Магнитный азимут (Am)– двугранный плоскостью магнитного меридиана и плоскостью, проходящей через заданное направление и центр Земли.

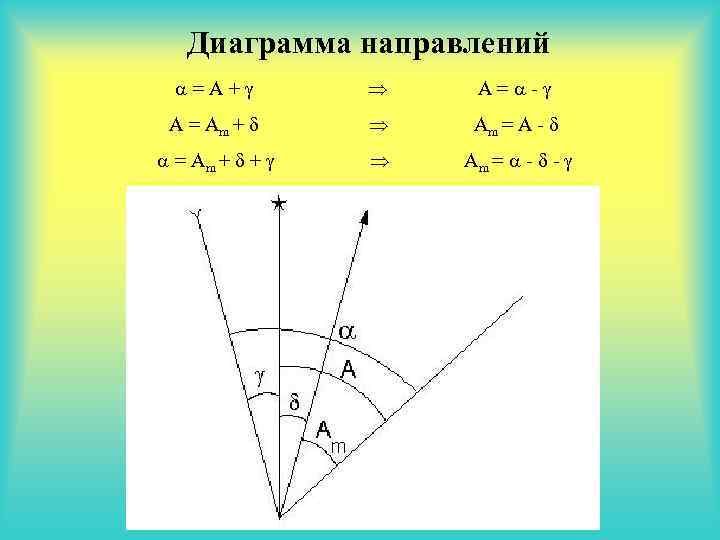
Диаграмма направлений = A + A = - A = Am + Am = A - = Am + + Am = - -

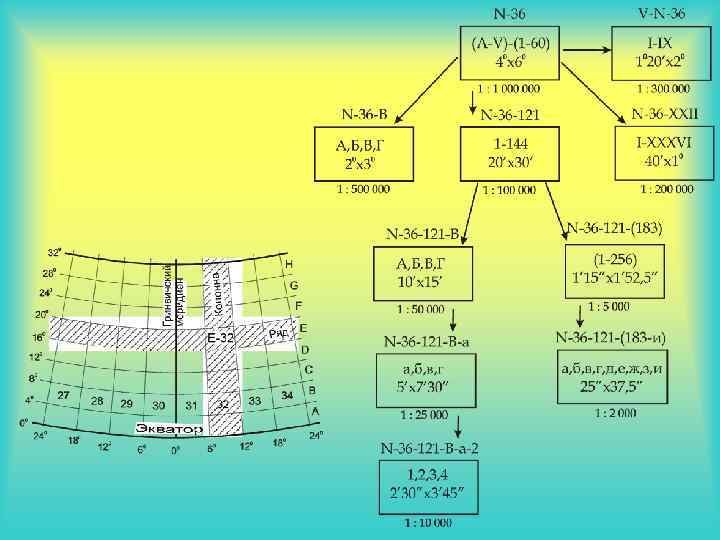
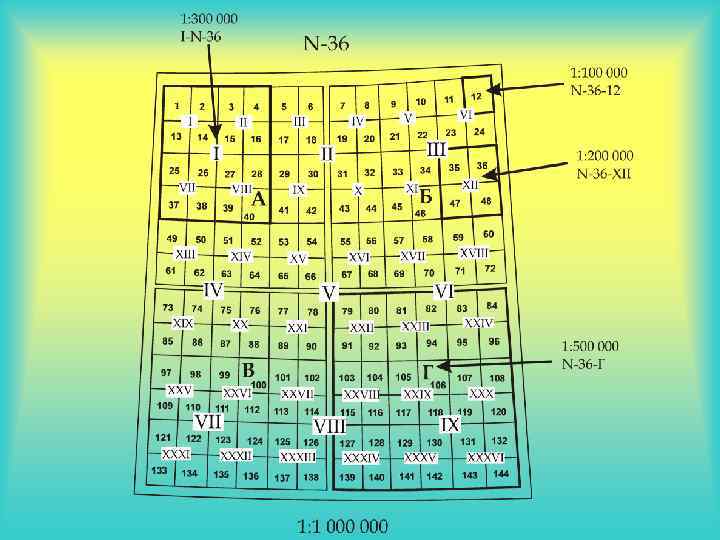
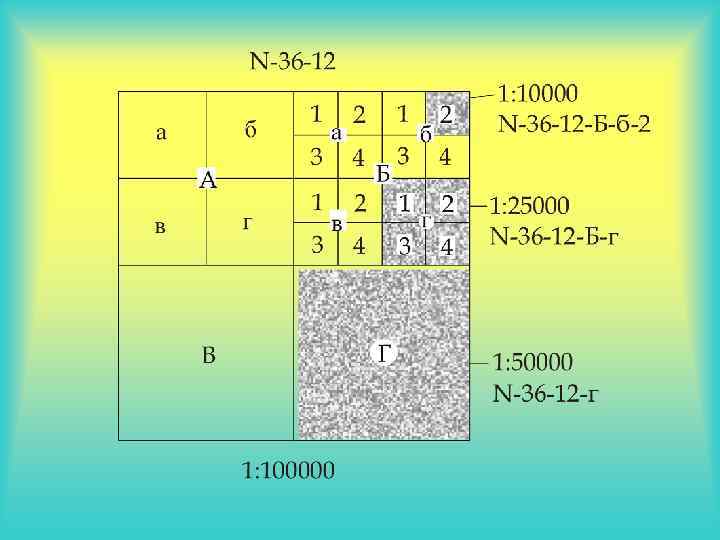
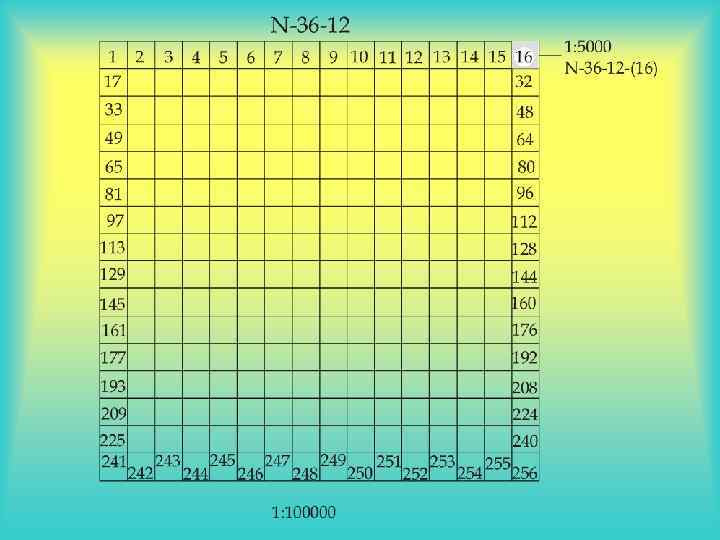
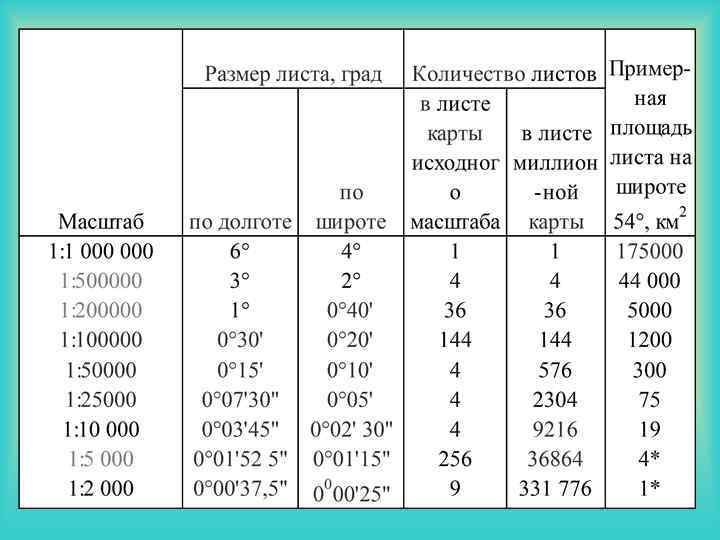
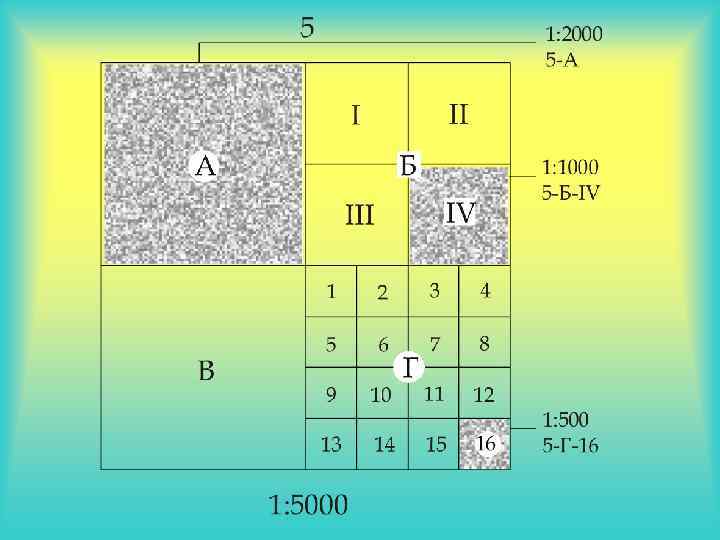
Разграфка и номенклатура Разграфкой называется порядок разделения карт мелких масштабов на отдельные листы карт более крупных масштабов. Номенклатурой называют правила обозначения листов карт разных масштабов