Genomes are large systems with small-system statistics Genome

Genomes are large systems with small-system statistics: Genome Growth by Duplication National Tsinghua University February 19, 2003 Institute of Physics, Academia Sinica March 20, 2003 HC Lee Dept Physics & Dept Life Sciences National Central University

Plan of Presentation • Introduction • Frequency of words in genomes • Large system & small-system statistics • Model for genome growth & evolution • Some results • Discussion - The RNA world, spandrels, codons, punctuated equilibrium, the Universal Ancestor, etc. • Outlook

The Book of Life

Many completed genomes Many. Bacteria 細菌 (about 80 organisms); completed genomes 1995 -2002 – 0. 5 -5 Mb; hundreds to 2000 genes 1996 April – Yeast 酵母 (Saccharomyces cerevisiae) 12 Mb, 5, 500 genes 1998 Dec. - Worm 線蟲 (Caenorhabditis elegans) 97 Mb, 19, 000 genes 2000 March – Fly 果蠅 (Drosophila melanogaster) 137 Mb, 13, 500 genes 2000 Dec. - Mustard 芥末子 (Arabidopsis thaliana) 125 Mb, 25, 498 genes 2001 Feb. – Human 人類 (Homo sapiens) 3000 Mb, 35, 000~40, 000 genes CBL@NCU

New way to do Life Science Research • in vivo 在活體裡 • in vitro 在試管中 • in silico 在 電腦中 CBL@NCU

Life Science in silico CBL@NCU = [biology] + [computer-science] + [math & physics] + [sequence data] “It is much easier to teach biology to people from a math, physics or computer-science background than to teach a biologist how to code well. ” - Nature, February 15, 2001, p 963

Two approaches to Life Science • Local - “Biology” – Individual, specificity, uniqueness • Global - “Physics” – Class, generality, universality Today’s talk: Global treatment of microbial genome Identify universality Hypothesis for early growth of universal ancestral genome

Structure of genome is complex • Many levels – genes, intergenic region, regulatory sections • Gene – network of introns and exons • Genome – network of genes • Random mutation • Genes are products of “blind watchmaker” • Once made, gene is repeatedly copied – paralogues, orthologues and pseudogenes • Genes are protected against rapid mutation

Genome as text • Genome is a text of four letters – A, C, G, T • Frequencies of k-mers characterize the whole genome – E. g. counting frequencies of 7 -mers with a “sliding window” N(GTTACCC) = N(GTTACCC) +1

Textual statistics of genome almost random but NOT TRIVIALLY so • Looks like a random text to casual observer • We know parts of it are coded – Coded text also appears random but occupies almost no volume in space of all tests • Very hard to construct dictionary • Distribution of frequencies of k-mers – Characterizes whole genomes – Similar in coding and non-coding regions – For short oligos width of distribution many times (up to 80) wider than normal – Disparity greater for smaller k • Similar for other kinds of distributions

21 century random text generator - Courtesy PY Lai

Genomes violently disobey rule of large systems • Large systems have sharply defined averages • Genomes are large texts with very fuzzy averages – There are 64 3 -letter words (3 -mers), each should appear 15, 625 +/- 125 times in a 1 Mb long genome – In random sequence, chances one 3 -mer would appear more (less) than 24, 000 (8, 000) times is 10 -830 (10 -980) - In Treponema pallidum (syphilis; 1 Mb long), 6 3 mers (CGC, GCG, AAA, TTT, GCA, TGC) occur more than 24, 000 times and 2 (CTA, TAG) appear less than 8, 000 times

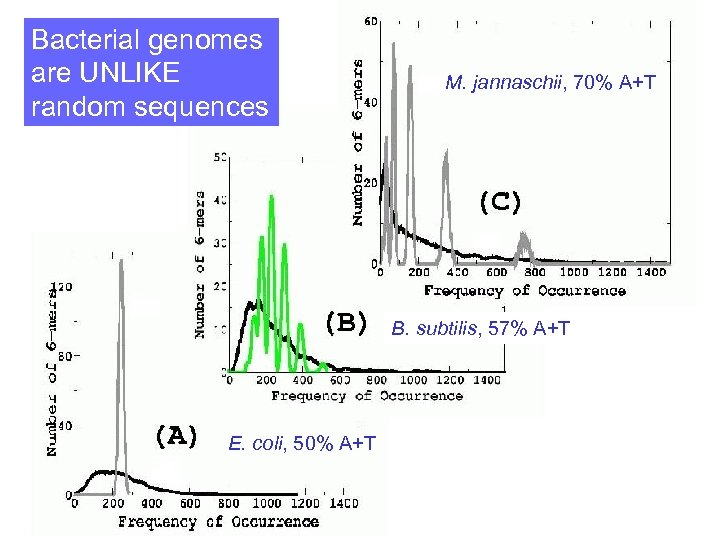Bacterial genomes are UNLIKE random sequences M. jannaschii, 70% A+T B. subtilis, 57% A+T E. coli, 50% A+T

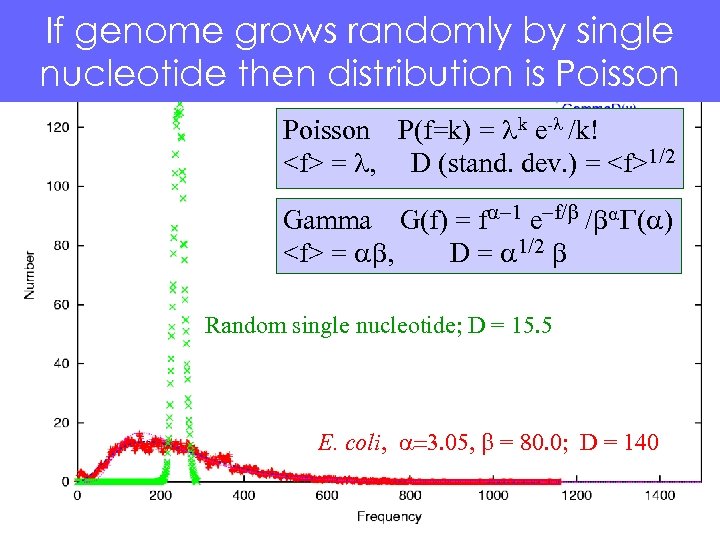If genome grows randomly by single nucleotide then distribution is Poisson P(f=k) = lk e-l /k! = l, D (stand. dev. ) = 1/2 Gamma G(f) = fa-1 e-f/b /ba. G(a) = ab, D = a 1/2 b Random single nucleotide; D = 15. 5 E. coli, a=3. 05, b = 80. 0; D = 140

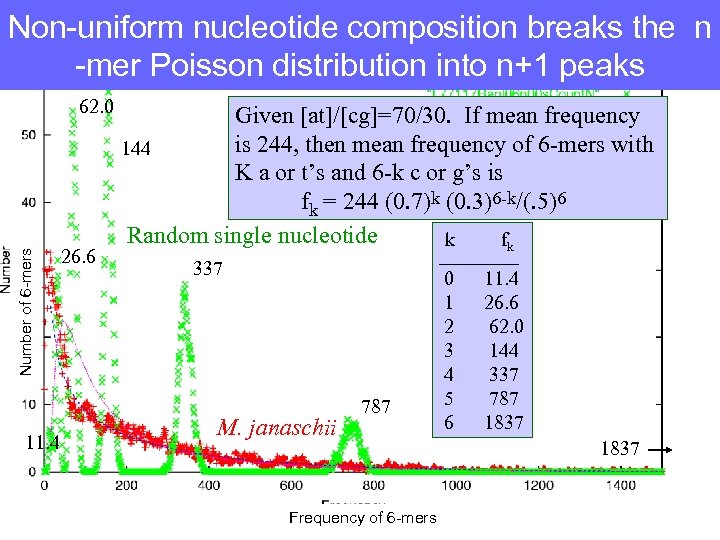Non-uniform nucleotide composition breaks the n -mer Poisson distribution into n+1 peaks Number of 6 -mers 62. 0 11. 4 26. 6 Given [at]/[cg]=70/30. If mean frequency is 244, then mean frequency of 6 -mers with 144 K a or t’s and 6 -k c or g’s is fk = 244 (0. 7)k (0. 3)6 -k/(. 5)6 Random single nucleotide k fk 337 M. janaschii 787 Frequency of 6 -mers ____ 0 11. 4 1 26. 6 2 62. 0 3 144 4 337 5 787 6 1837

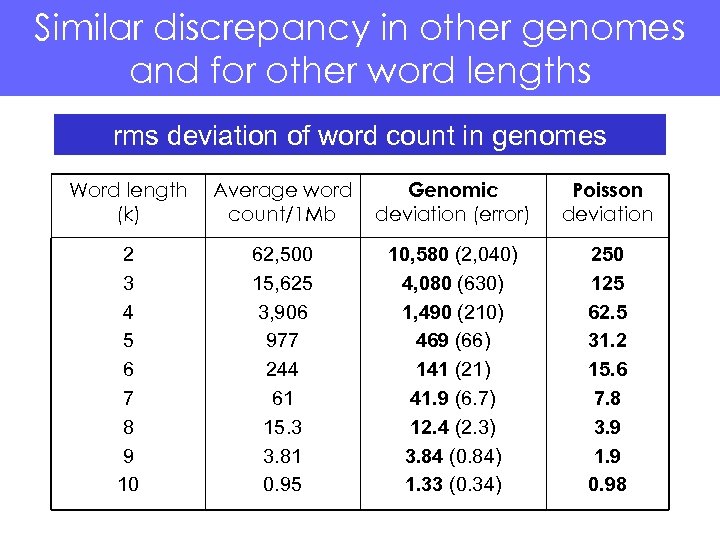Similar discrepancy in other genomes and for other word lengths rms deviation of word count in genomes Word length (k) Average word count/1 Mb Genomic deviation (error) Poisson deviation 2 3 4 5 6 7 8 9 10 62, 500 15, 625 3, 906 977 244 61 15. 3 3. 81 0. 95 10, 580 (2, 040) 4, 080 (630) 1, 490 (210) 469 (66) 141 (21) 41. 9 (6. 7) 12. 4 (2. 3) 3. 84 (0. 84) 1. 33 (0. 34) 250 125 62. 5 31. 2 15. 6 7. 8 3. 9 1. 9 0. 98

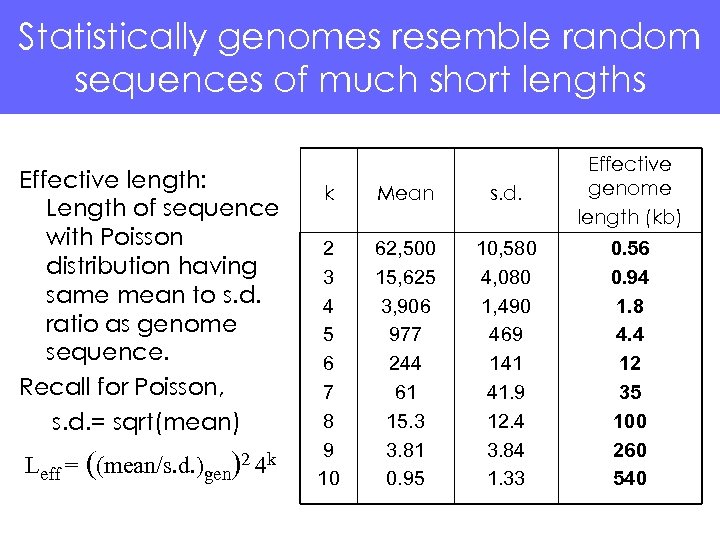Statistically genomes resemble random sequences of much short lengths Effective length: Length of sequence with Poisson distribution having same mean to s. d. ratio as genome sequence. Recall for Poisson, s. d. = sqrt(mean) Leff = ((mean/s. d. )gen)2 4 k k Mean s. d. Effective genome length (kb) 2 3 4 5 6 7 8 9 10 62, 500 15, 625 3, 906 977 244 61 15. 3 3. 81 0. 95 10, 580 4, 080 1, 490 469 141 41. 9 12. 4 3. 84 1. 33 0. 56 0. 94 1. 8 4. 4 12 35 100 260 540

How does a genome evolve and grow? • Evolve by random mutation – • Plus natural selection – – • Fitness acts only on phenotype, not directly on genome Selection is made on genome generated randomly Genome cannot grow through random mutation alone – • replacement, insertion, deletion Otherwise Poisson distribution Must grow to long length while retaining statistical characteristics of SHORT genome

The genome is a self plagiarizer • Genomes have many homologous genes • 50%, probably much more, of human genome composed of recent repeats – Many traces of repeats obliterated by mutation – Lower organisms may have longer genomes • Five types of repeats – transposable elements; processed pseudogenes; simple k-mer repeats; segmental duplications (10 -300 kb); (large) blocks of tandemly repeated sequences

A Hypothesis for Genome Growth • Random early growth • Followed by 1. random duplication and 2. random mutation Self copying – strategy for retaining and multiple usage of hard-to-come-by coded sequences (i. e. genes)

The Model • The genome grows by random single base addition from nothing to an initial length much shorter than final length • Thereafter the genome evolves by random mutation and random duplication, with a fixed frequency ratio

The Model (continued) • Mutation is standard single-point replacement (no insertion and deletion) • Segmental duplication involves three stochastic steps – random selection of site of copied segment – weighed random selection of length of copied segment – random selection of insertion site of copied segment

Stochastic selection of the length of self-copied segments • Use Erlang density distribution function for segment length l f(l) = 1/(s m!) (l/s)m exp(-l/s) (gamma function when m is real) • Mean < l > = (m+1) s standard deviation = (m+1)½ s Nothing special about this particular function, but mean and s. d. important

First generation result LS Hsieh, LF Luo, FM Ji and HCL, PRL 90 (2003) 18101 • Distribution of 6 -mer frequency • Starting genome length 1000 • Final genome length 1 million • Mutation to duplication event ratio 100 < h < 4000 • Length scale for copied segments 2500 < s < 100 K • Compared with E. coli (4. 5 Mbp), B. subtilis (4. 2 Mbp), M. jannaschii (1. 7 Mbp) (all normalized to 1 Mbp)

Number of 6 -mers E. coli [at]/[cg]=50/50 E. coli vs mutation + repeat Ratio 500: 1 Sigma = 15 k D= 140, 144 Frequency of 6 -mers E. coli vs random D= 140, 15. 5

Number of 6 -mers B. subtilis [at]/[cg]=60/40 B. subtilis vs mutation + repeat Ratio 600: 1 Sigma = 15 k D= 167, 169 Frequency of 6 -mers B. subtilis vs random D= 167, 79

Number of 6 -mers M. jannaschii [at]/[cg]=70/30 M. jannaschii vs mutation + repeat Ratio 600: 1 Sigma = 15 k D= 320, 321 Frequency of 6 -mers M. jannaschii vs random D= 320, 265

Gamma function reproduce higher moments Organism [at]/[gc] a b D(2) D(3) D(4) D(5) E. coli 50/50 gamma distribution 3. 05 80. 0 radom w/o self-copy (Poisson) w/ self-copy (h = 500 s = 15 K) 140 15. 6 144 147 146 3. 6 148 213 208 20. 7 212 252 243 10 247 B. subtilis 60/40 gamma distribution 2. 12 115 radom w/o self-copy (Poisson/7) w/ self-copy (h = 600 s = 15 K) 168 79 169 223 186 68 194 316 261 109 266 400 310 117 311 M. jannaschii 70/30 gamma distribution 0. 58 418 radom w/o self-copy (Poisson/7) w/ self-copy (h = 600 s = 15 K) 320 264 321 465 439 369 462 650 609 500 635 810 767 603 783 Gamma distribution: D(n) = (<(x - )n>)1/n; D(x) = xa-1 b-a exp(-x/b)/G(a) = 244 = a b; D(2) = a 1/2 b

What about other k’s? • Initial model good for k=6 but for other k’s not so good. Over-compensation (too broad) when k>6 and under-compensation (too narrow) when k<6. • Good result for k=6 (length = 1 Mb) requires h ~ 0. 04 s. In the limit of very small mutation to duplication event ratio, or h ~1, s ~25 b. • New model with short duplication length, s ~ 25 b, and without mutation.

Density function for duplication segment length • Recall Erlang density distribution function has mean and rms deviation < l > = (m+1) s; Dl = sqrt(m+1) s • For < l > = 25, have: m s 0 25 2 8 4 5 Dl 25 14 11 Good!

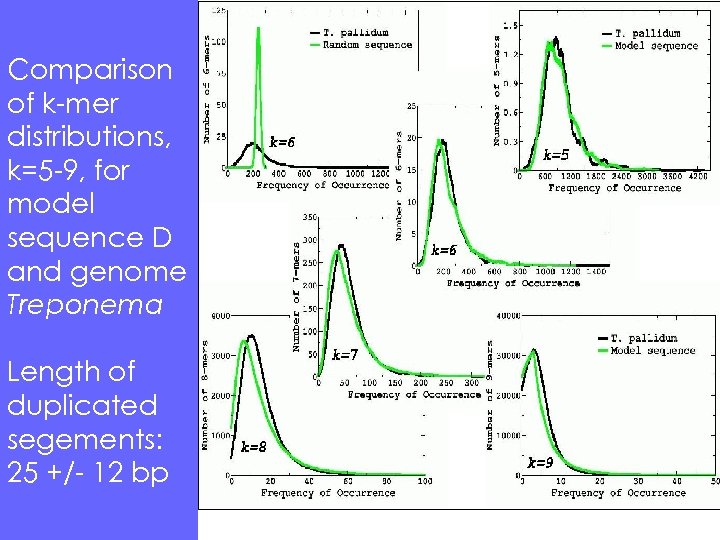Comparison of k-mer distributions, k=5 -9, for model sequence D and genome Treponema Length of duplicated segements: 25 +/- 12 bp

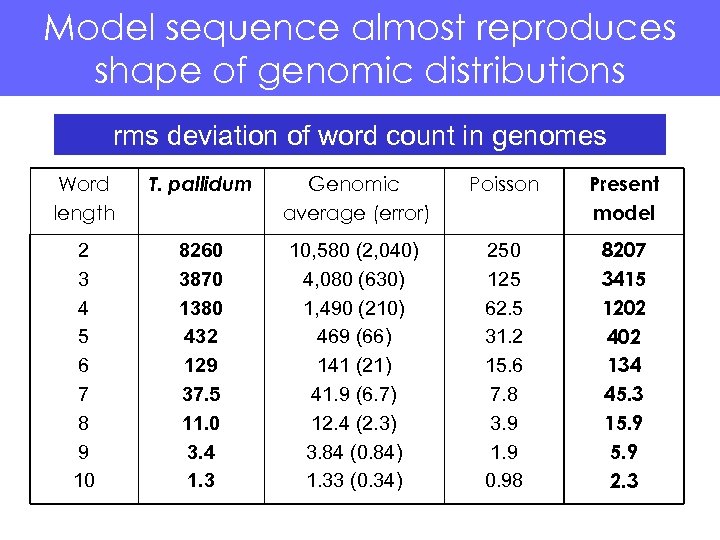Model sequence almost reproduces shape of genomic distributions rms deviation of word count in genomes Word length T. pallidum Genomic average (error) Poisson Present model 2 3 4 5 6 7 8 9 10 8260 3870 1380 432 129 37. 5 11. 0 3. 4 1. 3 10, 580 (2, 040) 4, 080 (630) 1, 490 (210) 469 (66) 141 (21) 41. 9 (6. 7) 12. 4 (2. 3) 3. 84 (0. 84) 1. 33 (0. 34) 250 125 62. 5 31. 2 15. 6 7. 8 3. 9 1. 9 0. 98 8207 3415 1202 402 134 45. 3 15. 9 2. 3

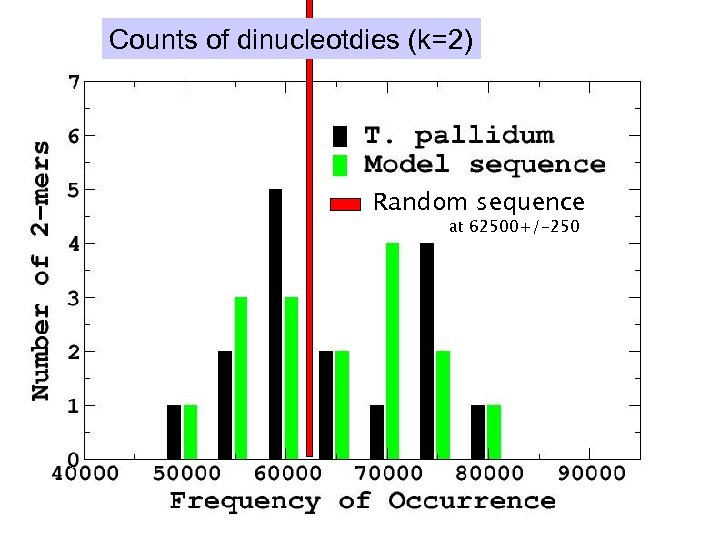Counts of dinucleotdies (k=2) Random sequence at 62500+/-250

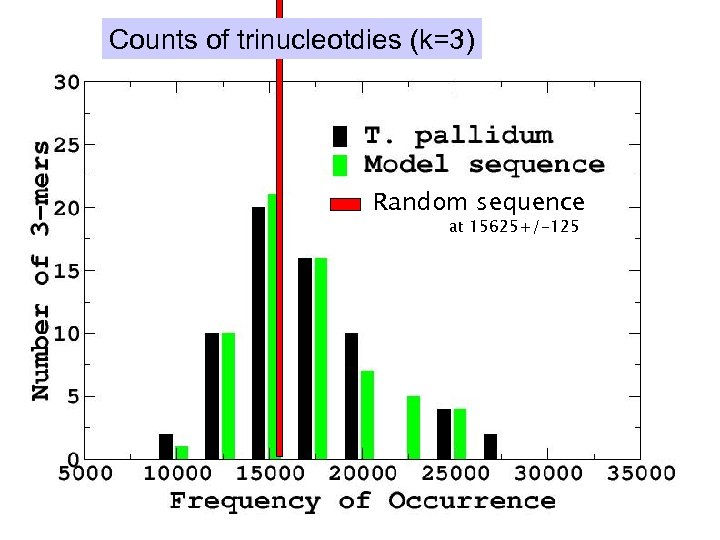Counts of trinucleotdies (k=3) Random sequence at 15625+/-125

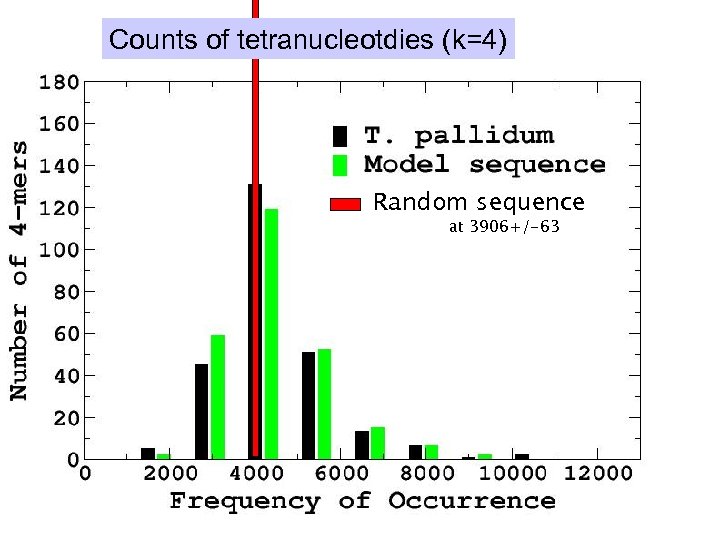Counts of tetranucleotdies (k=4) Random sequence at 3906+/-63

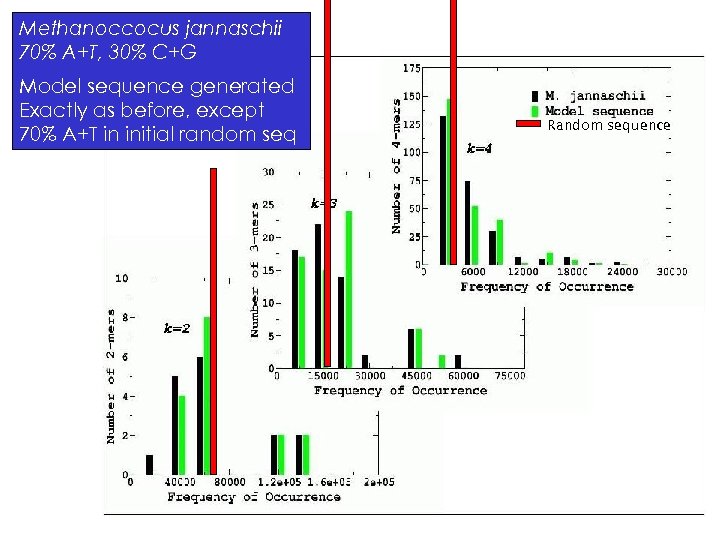Methanoccocus jannaschii 70% A+T, 30% C+G Model sequence generated Exactly as before, except 70% A+T in initial random seq Random sequence

Result sensitive to parameters • Paremeter values for “good” model sequence: - Initial random sequence length L 0 ~1 kb; - Mean copied segment length ~ 25 b - rms Dl ~ 12 b If L 0 > 10 kb, no good results If = 15 b, sequence too random for k<5 If = 40 b, sequence too choppy for k>6 If = 25 b, Dl ~ 15 b; agreement worsens

Discussion: The RNA World • RNA was discovered in early 80’s to have enzymatic activity – ribozymes can splice and replicate DNA sequences (Cech et al. (1981), Guerrier-Takada et al. 1983) • The RNA world conjecture – early had no proteins, only RNAs, which played the dual roles of genotype and phenotype • Some present-day ribozymes are very small; smallest hammerhead ribozyme only 31 nucleotides; ribozymes in early life need not be much larger

RNA World & size of early genome • In our model the small initial size of the genome necessarily implies an early RNA world • A genome ~ 1 K nt long is long enough to code the many small ribozymes (but not proteins) needed to propagate life • Origin of this initial genome not addressed in the model. It (or its presursor) could have arisen spontaneously - artificial ribozymes have been succcessfully isolated from pools of random RNA sequences (Ekland et al. 1995)

RNA World & length of duplicated segments • Recall that present-day ribozyme can be as small as 31 nt • The average duplicated segment length of 25 nt in the model is very short compared to present-day genes that code for proteins, but likely represents a good portion of the length of a typical ribozyme encoded in the early universal genome of the RNA world

Are codons “spandrels”? • Spandrels – In architecture - the roughly triangular space between an arch, a wall and the ceiling – In evolution – major category of important evolutionary features that were originally side effects and did not arise as adaptations (Gould and Lewontin 1979) • Wide 3 -mer/codon distribution or natural selection, which came first?

Are codons “spandrels”? (cont’d) • Frequency of 3 -mer distribution in genomes is about 40 x wider than Poisson. Was the widening caused by – Uneven codon usage + natural selection? Or, – Genome growth by segmental duplication? • In RNA world, codons came after RNA and existence of replication machinery. Hence the following scenario: RNA + recombination > genome growth by stochastic dupliction > extreme bias in 3 -mer population > rise of codon • In our model, codons are most likely spandrels

More spandrels • Same goes with other oligonucleotides Many oligonucleotides that are grossly overor under-represented have biological functions. Evolution being an opportunistic process, these oligonucleotides could have been drafted to serve special biological purposes because they had already been made very copious or very rare by stochastic genome growth

Duplication continued and expanded after the rise of proteins • In bacterial genomes typically about 12% of genes represent recent duplication events – Average gene is about 1000 bases long. Suggest about 12% of genome generated by duplications of ~ 1000 b segments. Not yet incorporated into the model. • In higher organisms a large number of repeat sequences with lengths ranging from 1 base to many kilobases are believed to have resulted from at least five modes of duplication

Grow by duplication (of gene-size segments) may explain: • How have genes been duplicated at the high rate of about 1% per gene per million years? (Lynch 2000) • Why are there so many duplicate genes in all life forms? (Maynard 1998, Otto & Yong 2001) • Was duplicate genes selected because they contribute to genetic robustness (by protecting the genome against harmful mutations)? (Gu et al. 2003) – Likely not; Most likely high frequency of occurrence duplicate genes is a spandrel

Classical Darwinian Gradualism or Punctuated equilibrium? • Great debated in palaeontology and evolution - Dawkins & others vs. (the late) Gould & Eldridge: evolution went gradually and evenly vs. by stochastic bursts with intervals of stasis Our model provides genetic basis for both. Mutation and small duplication induce gradual change; occasional large duplication can induce abrupt and seemingly discontinuous change

Discussion (cont’d) • Phylogeny and the Universal Ancestor – If extremely frequent and extremely rare oligos (EFERO) are the remnants of much shorter early sequence, then there should exist such a short sequence during some stage of the genome growth. – Then we may be able to use the set of EFEROs in whole genomes to construct phylogenetic trees of whole genomes. – At each node of the tree would be an ancestor sequence characterized by a set of EFEROs. – The ancestor of Life would be characterized by the minimum set of EFEROs.

Summary • Distribution of frequency of k-mers in bacterial genomes hugely wider than Poisson – larger for smaller k • Can be explained by simple two-phase genome growth model: – first grow to short (~1 kb) random sequence – then grow by random duplications of segments of length 25 +- 12 b long • Reproduces genomic statistics for k=2 -8 • Universal ancestral genome lived in an RNA world – Replication carried by ribozymes ~ 30 nt; – Codons and many signal sequences are spandreals

Outlook • Need to understand distribution for ALL k’s – There are repeated k-mers of k up to ~1000 • Other oddities – E. g. Distribution of entropies of k-mers • Empirical verification – Can duplication growth be independently verified? • Time scale – When did growth happen? At what rate? How did growth stabilize? Has it stabilized? • Phylogeny – Can we build a good tree based on model? Can we learn anything about the Universal Ancestor ? Is there a Universal Ancestor ?

CBL Lab @NCU Collaborators Phys. & Life Sci. * L. C. Hsieh # J. L. Lo # T. Y. Chen # J. P. Yiu # Z. Y. Guo # Z. R. Chiu # H. Y. Bai # C. H. Chang # H. D. Chen # W. L. Fan # J. Z. Horng # F. M. Lin Horng Lab, NCU, Comp. Sci. *L. F. Luo Univ. Outer Mongolia *F. M. Ji Beijing Jiaotong Univ. Rosie Redfied Zoology, UBC *This work; # students * # All simulation in this work done by L. C. Hsieh

Thank you for your attention

Genomes are large systems with small-system statistics: Genome Growth by Duplication Lecture II Winter School on Modern Biophysics National Taiwan University December 16 -18, 2002 HC Lee Dept Physics & Dept Life Science National Central University

Result sensitive to values of two parameters • Mutation to duplication event ratio h – bacterial genomes, 200 < h ~ 0. 04 s < 800 – If h >> 800 (@ s ~ 15 K) • too many mutations • gets long genome with Poisson distribution – If h << 200 (@ s ~ 15 K) • too much duplication • too few mutations • gets multiple copies of random short (initial) genome (distribution too wide)

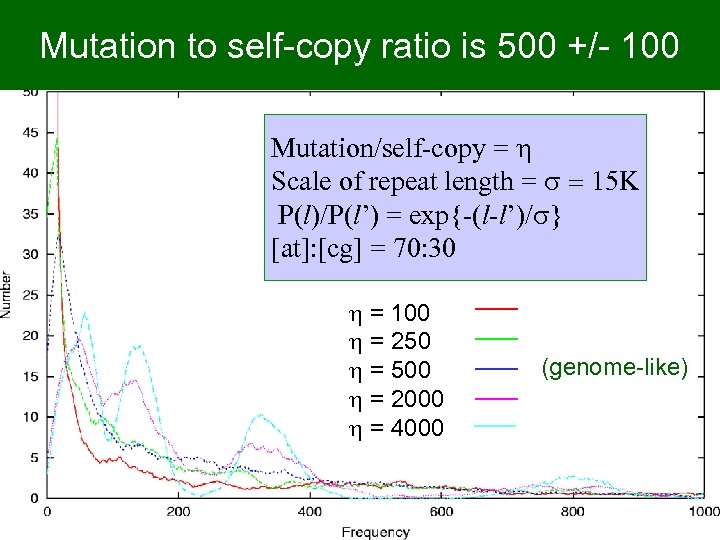Mutation to self-copy ratio is 500 +/- 100 Mutation/self-copy = h Scale of repeat length = s = 15 K P(l)/P(l’) = exp{-(l-l’)/s} [at]: [cg] = 70: 30 h = 100 h = 250 h = 500 h = 2000 h = 4000 (genome-like)

Result sensitive to values of two parameters (cont’d) • Length scale s for copied segments – s ~ 10 K to 25 K for bacterial genomes – If s << 5 K (@ h ~ 600) • genome grows too slowly • too many mutations • gets long genome with Poisson distribution – If s >> 25 K (@ h ~ 600) • genome grows too quickly • too few mutations • gets multiple copies of random short (initial) genome (distribution too wide)

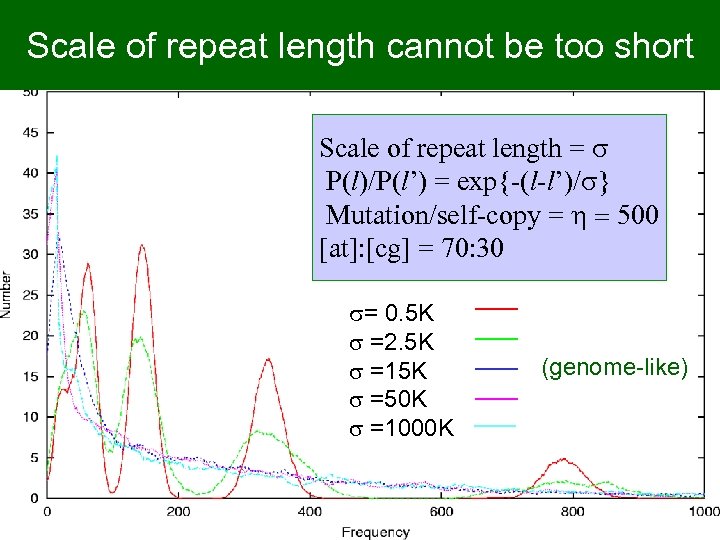Scale of repeat length cannot be too short Scale of repeat length = s P(l)/P(l’) = exp{-(l-l’)/s} Mutation/self-copy = h = 500 [at]: [cg] = 70: 30 s= 0. 5 K s =2. 5 K s =15 K s =50 K s =1000 K (genome-like)

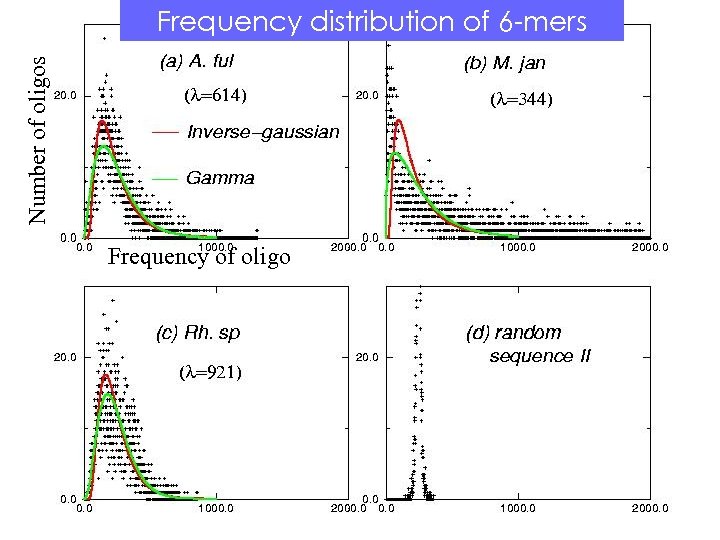Number of oligos Frequency distribution of 6 -mers Frequency of oligo