Genetic Programming for Financial Trading Nicolas NAVET INRIA

Genetic Programming for Financial Trading Nicolas NAVET INRIA, France AIECON NCCU, Taiwan http: //www. loria. fr/~nnavet http: //www. aiecon. org/ Tutorial at CIEF 2006, Kaohsiung, Taiwan, 08/10/2006

Outline of the talk (1/2) n PART 1 : Genetic programming (GP) ? GP among machine learning techniques n GP on the symbolic regression problem n n n Pitfalls GP PART 2 : GP for financial trading Various schemes n How to implement it ? n Experimentations : GP at work n 2

Outline of the talk (2/2) n PART 3 : Analyzing GP results Why GP results are usually inconclusive? n Benchmarking with n “Zero-intelligence trading strategies” n “Lottery Trading” n Answering the questions n n “is there anything to learn on the data at hand” n “is GP effective at this task” n PART 4 : Perspectives 3

GP is a Machine Learning technique n n n Ultimate goal of machine learning is the automatic programming, that is computers programming themselves. . More achievable goal: “Build computer-based systems that can adapt and learn from their experience” ML algorithms originate from many fields: mathematics (logic, statistics), bio-inspired techniques (neural networks), evolutionary computing (Genetic Algorithm, Genetic Programming), swarm intelligence (ant, bees) 4

Evolutionary Computing n Algorithms that make use of mechanisms inspired by natural evolution, such as n n n “Survival of the fittest” among an evolving population of solutions Reproduction and mutation Prominent representatives: n n è Genetic Algorithm (GA) Genetic Programming (GP) : GP is a branch of GA where the genetic code of a solution is of variable length Over the last 50 years, evolutionary algorithms have proved to be very efficient for finding approximate solutions to algorithmically complex problems 5

Two main problems in Machine Learning n Classification : model output is a prediction whether the input belongs to some particular class n n Examples : Human being recognition in image analysis, spam detection, credit scoring, market timing decisions Regression : prediction of the system’s output for a specific input n Example: predict tomorrow's opening price for a stock given closing price, market trend, other stock exchanges, … 6

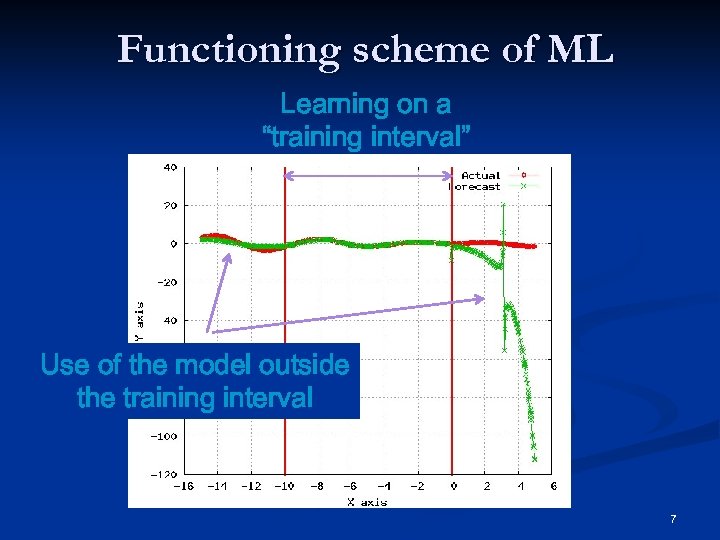Functioning scheme of ML Learning on a “training interval” Use of the model outside the training interval 7

GP basics

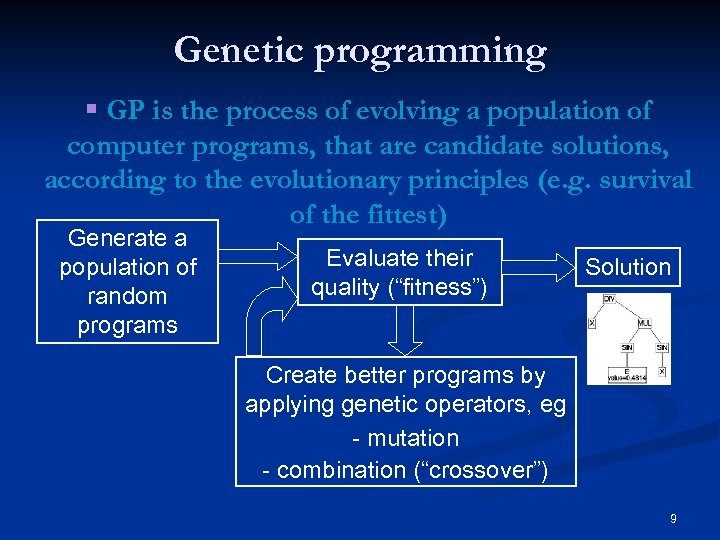Genetic programming § GP is the process of evolving a population of computer programs, that are candidate solutions, according to the evolutionary principles (e. g. survival of the fittest) Generate a population of random programs Evaluate their quality (“fitness”) Solution Create better programs by applying genetic operators, eg - mutation - combination (“crossover”) 9

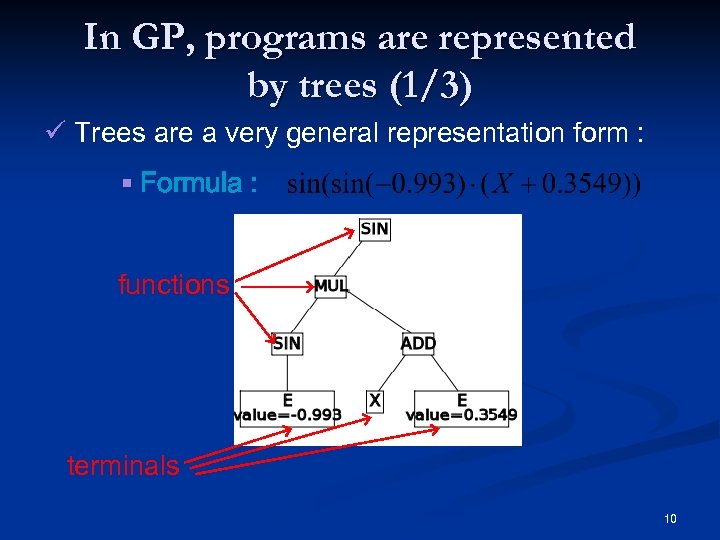In GP, programs are represented by trees (1/3) ü Trees are a very general representation form : § Formula : functions terminals 10

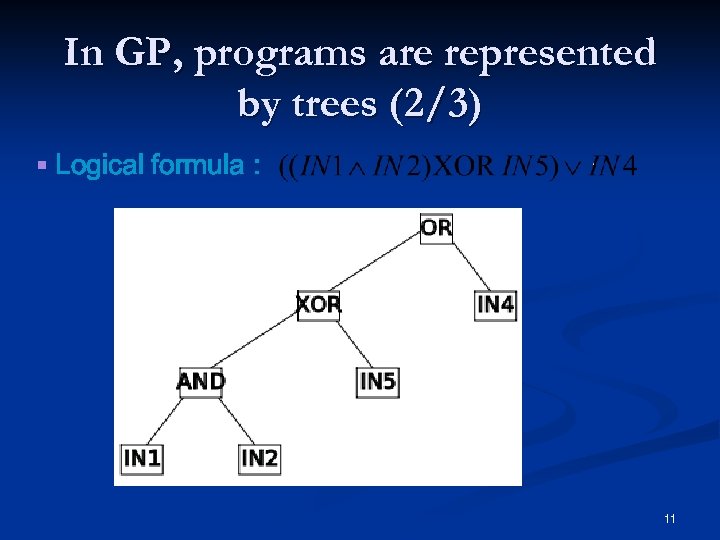In GP, programs are represented by trees (2/3) § Logical formula : 11

In GP, programs are represented by trees (3/3) § Trading rule formula : BUY IF (VOL>10) AND (Moving Average(25) > Moving Average(45)) Picture from [Bh. Pi. Zu 02] 12

Preliminary steps of GP § The user has to define : § the set of terminals § the set of functions § how to evaluate the quality of an individual: the “fitness” measure § parameters of the run : e. g. number of individuals of the population § the termination criterion 13

Symbolic regression : a problem GP is good at … § Symbolic regression : find a function that fits well a set of experimental data points § “Symbolic” means that one looks for both - the functional form - the value of the parameters, e. g. è Differs from other regressions where one solely looks for the best coefficient values for a pre-fixed model. Usually the choice of the model is the most difficult issue ! 14

Symbolic regression n Given a set of points : § Find the function s. t. “as far as possible” : § Possible fitness function : § GP functions : § GP terminals : 15

GP Operators : biologically inspired … n n n Recombination (aka “crossover”) : 2 individuals share genetic material and create one or several offsprings Mutation : introduce genetic diversity by random changes in the genetic code Reproduction : individual survives ‘as is’ in the next generation 16

Selection Operators for Crossover/reproduction § General principles : in GP the fittest individuals should have more chance to survive and transmit their genetic code § Fitness proportionate : each individual is selected with a probability that depends on the value of its fitness § Rank based : each individual is selected with a probability function of its rank according to the fitness order § Tournament selection of size n : n individuals are randomly chosen and the best is kept 17

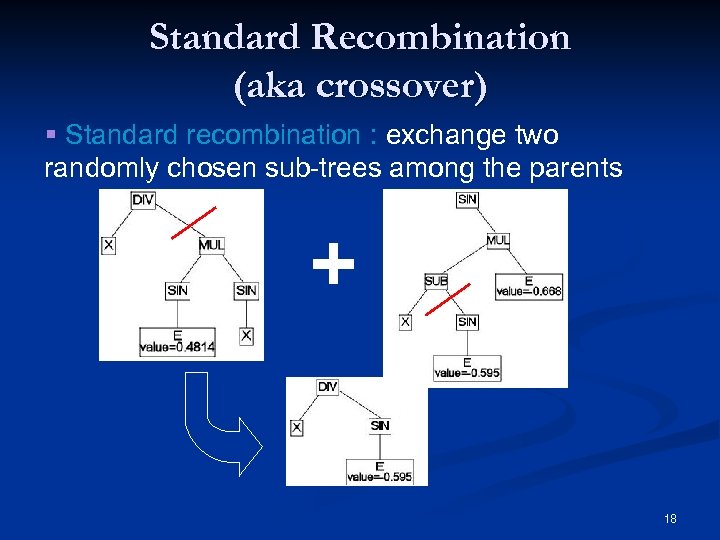Standard Recombination (aka crossover) § Standard recombination : exchange two randomly chosen sub-trees among the parents + 18

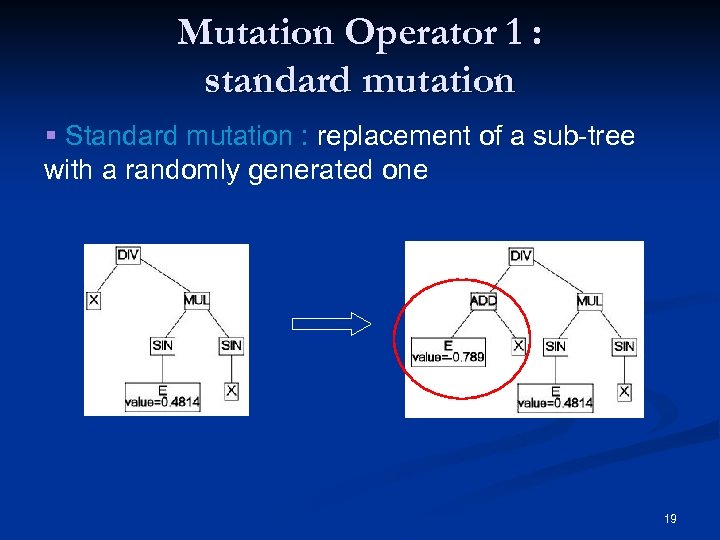Mutation Operator 1 : standard mutation § Standard mutation : replacement of a sub-tree with a randomly generated one 19

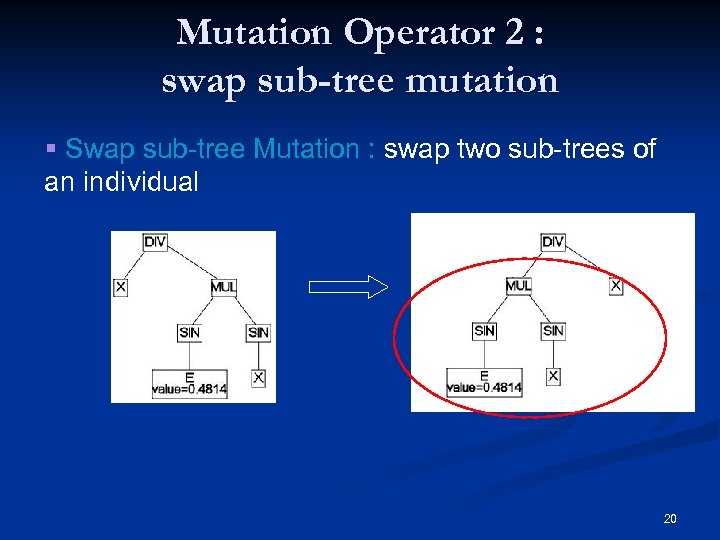Mutation Operator 2 : swap sub-tree mutation § Swap sub-tree Mutation : swap two sub-trees of an individual 20

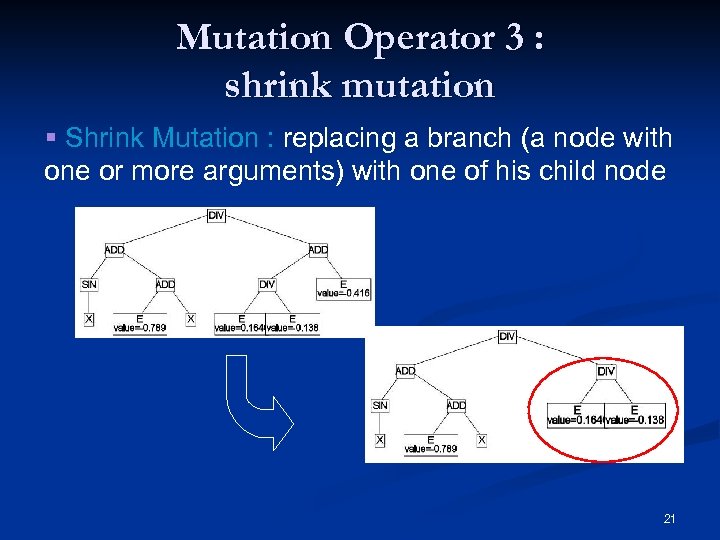Mutation Operator 3 : shrink mutation § Shrink Mutation : replacing a branch (a node with one or more arguments) with one of his child node 21

Other Mutation Operators § “Swap mutation” : (≠ swap sub-tree mutation) exchanging the function associated to a node by one having the same number of arguments § “Headless Chicken crossover” : mutation implemented as a crossover between a program and a newly generated random program § …. 22

Reproduction / Elitism Operators § Reproduction : an individual is reproduced in the next generation without any modification § Elitism : the best n individuals are kept in the next generation 23

GP is no silver bullet … 24

GP Issue 1 : how to choose the function set ? 1. The problem cannot be solved if the set of functions is not “sufficient”… 2. But “Non-relevant” functions increases uselessly the search space … è Problem : there is no automatic way to decide a priori the “relevant” functions and to build a “sufficient” function sets … 25

Problem cannot be solved if the set of functions is not “sufficient” : illustration n Generating function: SETUP § GP functions : § GP terminals : with and without sin(x) Number of individuals 500 Number of generations 20 Standard GP operators: crossover, mutation, reproduction, tournament selection of size 6, … 26

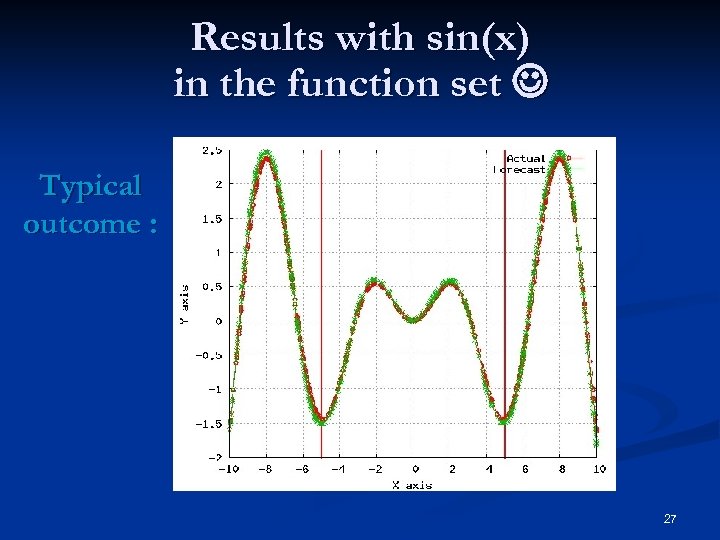Results with sin(x) in the function set Typical outcome : 27

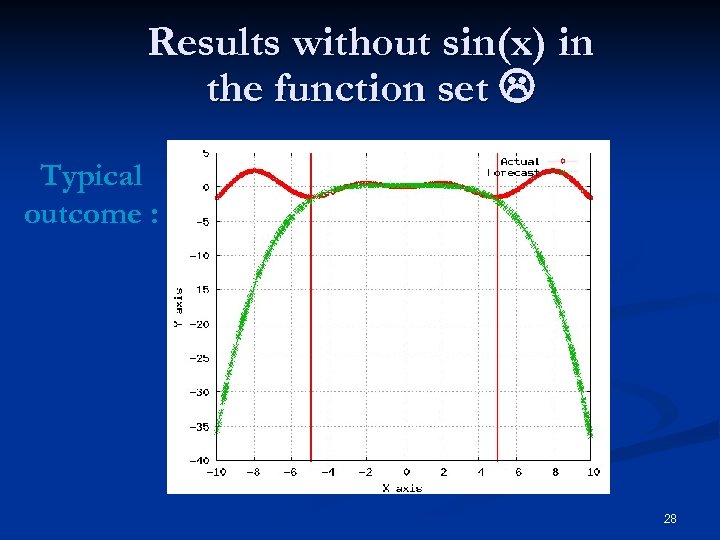Results without sin(x) in the function set Typical outcome : 28

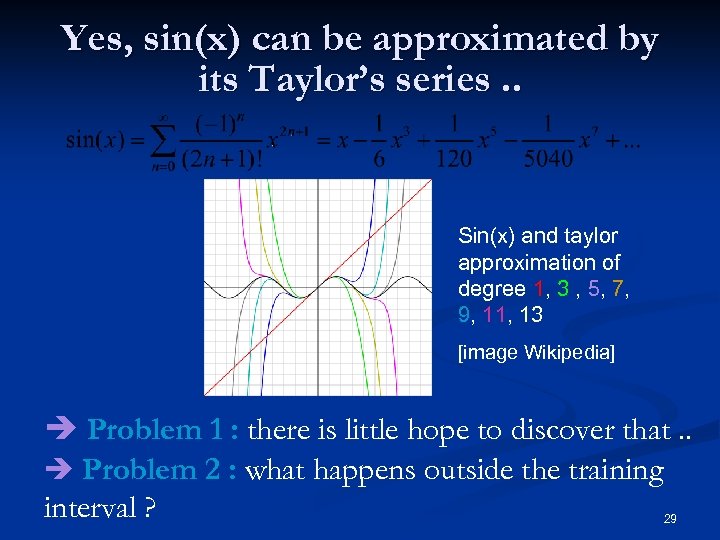Yes, sin(x) can be approximated by its Taylor’s series. . Sin(x) and taylor approximation of degree 1, 3 , 5, 7, 9, 11, 13 [image Wikipedia] è Problem 1 : there is little hope to discover that. . è Problem 2 : what happens outside the training interval ? 29

Composition of the function set is crucial : illustration § GP functions : § Subset is extraneous in this context … § Same experimental setup as before 30

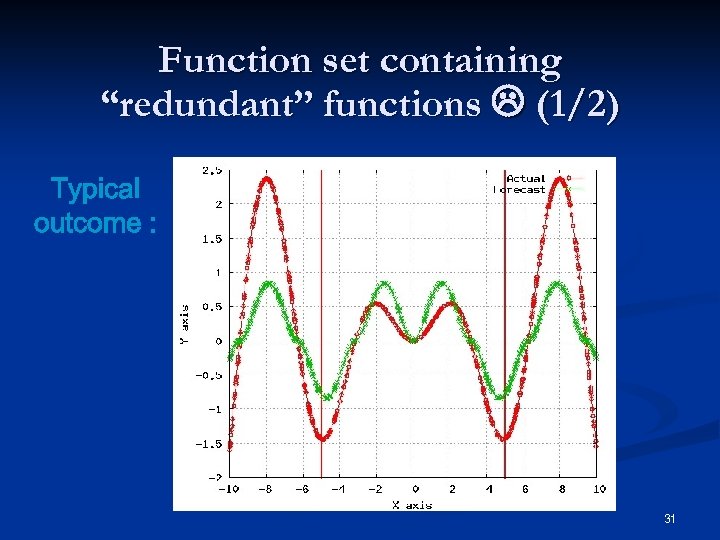Function set containing “redundant” functions (1/2) Typical outcome : 31

Function set containing “redundant” functions (2/2) è On average, with the “extraneous” functions the best solution is 10% farther from the curve in the training interval (much more outside!) è With the “extraneous” functions, the average solution is better. . because the tree is more likely to contain a trigonometric function 32

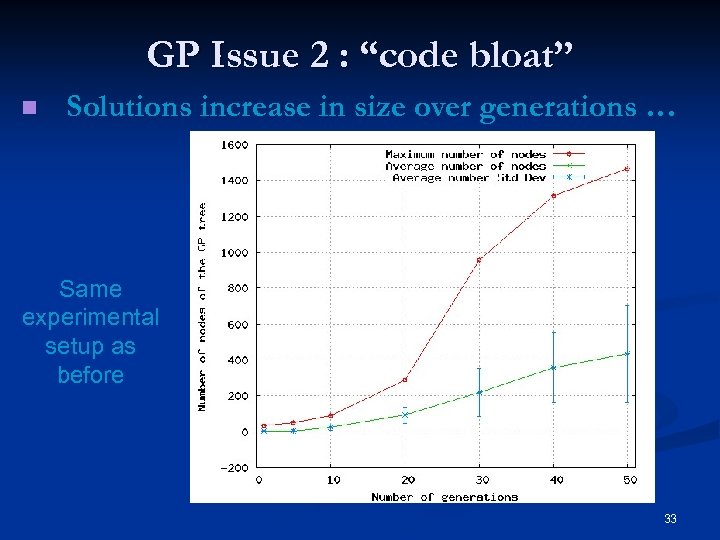GP Issue 2 : “code bloat” n Solutions increase in size over generations … Same experimental setup as before 33

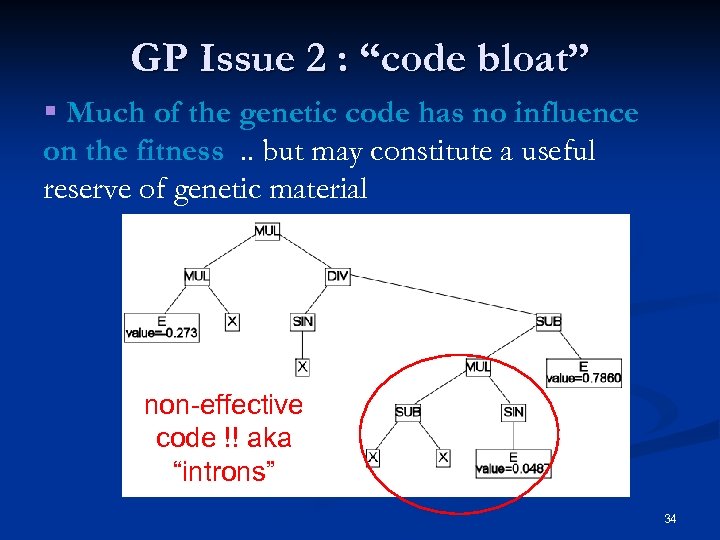GP Issue 2 : “code bloat” § Much of the genetic code has no influence on the fitness. . but may constitute a useful reserve of genetic material non-effective code !! aka “introns” 34

Code bloat: why is it a problem ? 1. Solutions are hard to understand : § learning something from huge solutions is almost impossible. . § One has no confidence using programs one does not understand ! 2. Much of the computing power is spent manipulating non-contributing code, which may slow down the search 35

Countermeasures. . (1/2) n Static limit of the tree depth n Dynamic maximum tree depth [Si. Al 03] : the limit is increased each time an outstanding individual deeper than the current limit is found n n Limit the probability of longer-than-average individuals to be chosen by reducing their fitness Apply operators than ensure limited code growth Discard newly created individuals whose “behavior” is too close to the ones of their parents (e. g. “behavior” for regression pb could be position of the points [Str 03]) … 36

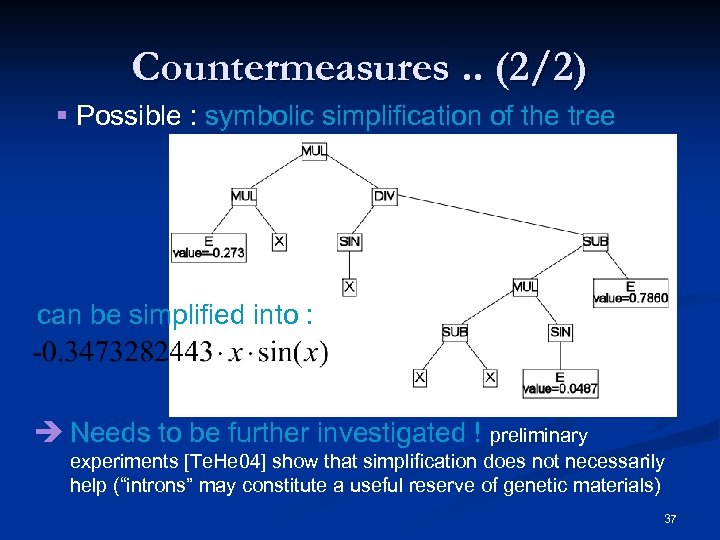Countermeasures. . (2/2) § Possible : symbolic simplification of the tree can be simplified into : è Needs to be further investigated ! preliminary experiments [Te. He 04] show that simplification does not necessarily help (“introns” may constitute a useful reserve of genetic materials) 37

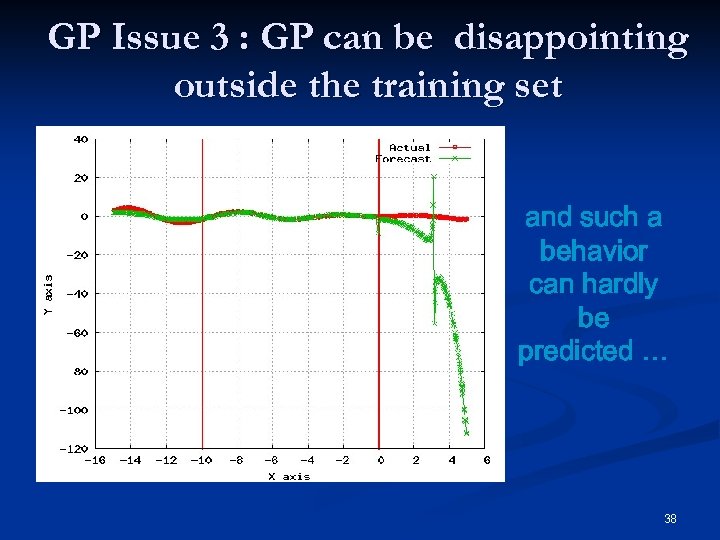GP Issue 3 : GP can be disappointing outside the training set and such a behavior can hardly be predicted … 38

GP Issue 3 : explanation (1/2) § Usually GP functions are implemented to have the closure property: “each function must be able to handle every possible value” § What to do with : • division by 0 ? • sqrt(x) with x < 0 ? • … § Solution: “protected operators”, eg. the division : if (abs(denominator) < value-near-0) return 1; 39

GP Issue 3 : explanation (2/2) § in our case, fragment of the best GP tree : Why did it not occur on the training interval ? - not training points chosen such that 40

GP Issue 4 : standard GP is not good at finding numerical constants (1/3) § Where do numerical values come from ? § “Ephemeral random constants” : random values inserted at the leafs of the GP trees during the creation of initial population § Use of arithmetic operators on existing numerical constants § Generation by combination of variables/functions: § Lately, many studies show that standard GP is not good at finding constants … 41

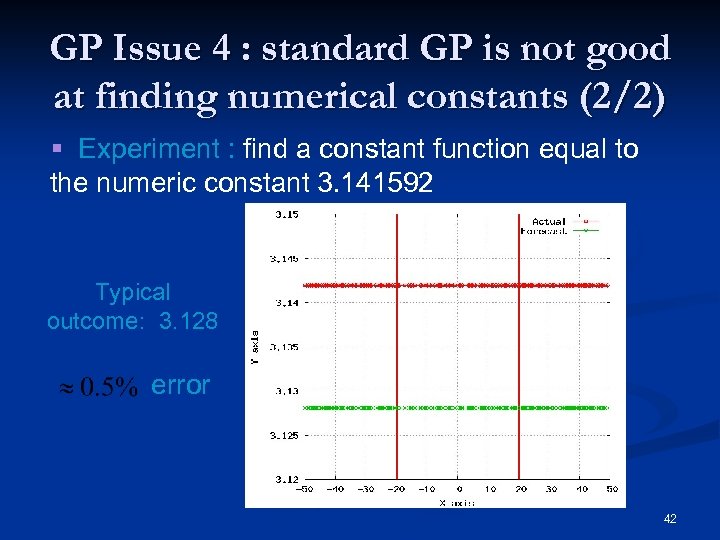GP Issue 4 : standard GP is not good at finding numerical constants (2/2) § Experiment : find a constant function equal to the numeric constant 3. 141592 Typical outcome: 3. 128 error 42

GP Issue 4 : standard GP is not good at finding numerical constants (3/3) § There are several more efficient schemes for constants generation in GP [Dem 95] : - local optimization [Zu. Pi. Ma 01], - numeric mutation [Ev. Fe 98], -… è One of them should be implemented otherwise 1) computation time is lost searching for constants 2) solutions may tend to be “bigger” 43

Some (personal) conclusions on GP (1/3) ü GP is undoubtedly a powerful technique : § Efficient for predicting / classifying. . but not more than other techniques § Symbolic representation of the created solutions may help to give good insight into the system under study. . not only the best solutions are interesting but also how the population has evolved over time è GP is a tool to learn knowledge … 44

Some (personal) conclusions on GP (2/3) ü Powerful tool but. . . § a good knowledge of the application field is required for choosing the right functions set § prior experience with GP is mandatory to avoid common mistakes – there is no theory to tell us what to do ! § it tend to create solutions too big to be analyzable -> countermeasures should be implemented § fine-tuning the GP parameters is very timeconsuming 45

Some (personal) conclusions on GP (3/3) ü How to analyze the results of GP ? § efficiency can hardly be predicted, it varies § from problem to problem § … and from GP run to GP run § if results are not very positive : § is it because there is no good solution ? § or GP is not effective and further work is needed ? è There are solutions – part 3 of the talk 46

Part 2 : GP for financial trading

Why GP is an appealing technique for financial trading ? n n Easy to implement / robust evolutionary technique Trading rules (TR) should adapt to a changing environment – GP may simulate this evolution Solutions are produced under a symbolic form that can be understood analyzed GP may serve as a knowledge discovery tool (e. g. evolution of the market) 48

GP for financial trading n n GP for composing portfolio (not discussed here, see [Lag 03] ) GP for evolving the structure of neural networks used for prediction (not discussed here, see [Go. Fe 99] ) GP for predicting price evolution (briefly discussed here, see [Kab 02] ) Most common : GP for inducing technical trading rules 49

Predicting price evolution : general comments. . n “Long term forecast of stock prices remain a fantasy” [Kab 02] è Swing trading or intraday trading Many other (more? ) efficient ML tools : e. g. SVM and NN è GP is anyway useful for ensemble methods n CIEF Tutorial 1 by Prof. Fyfe – today 1 h 30 pm ! n 2 excellent starting points : [Kab 02] : single-day-trading-strategy based on the forecasted spread è [Sa. Te 01]: winner of the CEC 2000 Dow-Jones Prediction – Prediction t+1, t+2, t+3, …, t+h - a solution has one tree per forecast horizon è 50

Predicting price evolution : fitness function n Definition of the fitness function has been shown to be crucial e. g. [Sa. Te 01], there are many possible : è (Normalized) Mean square error è Mean Absolute Percentage Error è (1 - ) statistic = 1 - MAPE / MAPE-Randow-Walk è Directional symmetry index (DS) è DS weighted by the direction and amplitude of the error è… Issue : a meaningful fitness function is not always “GP friendly” … n 51

Inducing technical trading rules Training interval 1 ) Creation of the trading rules using GP 2) Selection of the best resulting strategies Validation interval Further selection on unseen data Out-of-sample interval Performance evaluation One strategy is chosen for outof-sample 52

Steps of the algorithm (1/3) 1. Extracting training time series from the database 2. Preprocessing : cleaning, sampling, averaging, normalizing, … 53

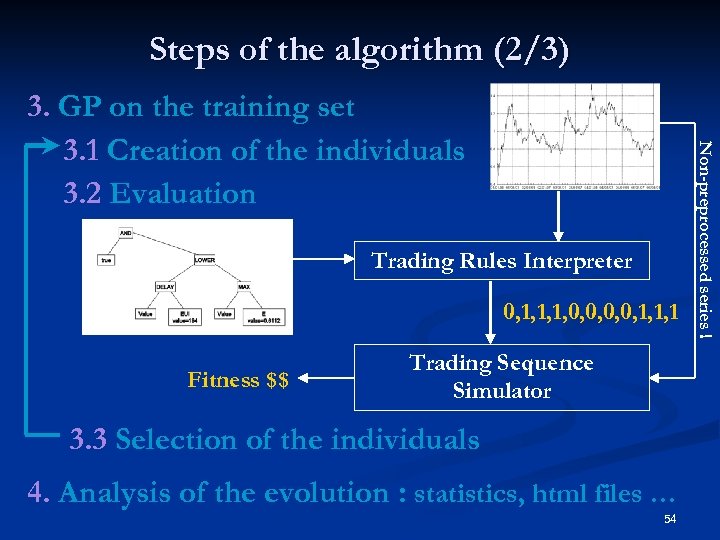Steps of the algorithm (2/3) Trading Rules Interpreter 0, 1, 1, 1, 0, 0, 1, 1, 1 Fitness $$ Trading Sequence Simulator 3. 3 Selection of the individuals 4. Analysis of the evolution : statistics, html files … 54 Non-preprocessed series ! 3. GP on the training set 3. 1 Creation of the individuals 3. 2 Evaluation

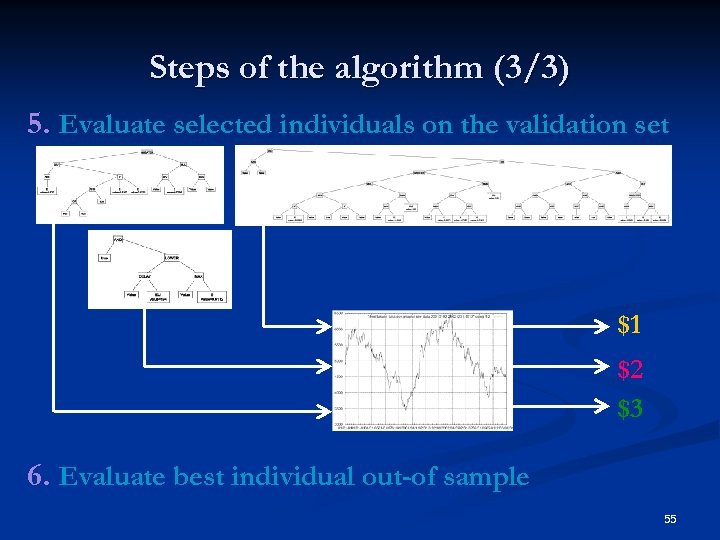Steps of the algorithm (3/3) 5. Evaluate selected individuals on the validation set $1 $2 $3 6. Evaluate best individual out-of sample 55

GP at work : Demo on the Taiwan Capitalization Weighted Stock Index

Part 3 : Analyzing GP results

One may cast doubts on GP efficiency. . n n Highly heuristic – no theory ! Problems on which GP has been shown not to be significantly better than random search Few clear-cut successes reported in the financial literature GP embeds little domain specific knowledge yet. . Doubts on the efficiency of GP to use the available computing time : n n code bloat bad at finding numerical constants best solutions are sometimes found very early in the run. . Variability of the results ! e. g. returns: -0. 160993, 0. 0526153, -0. 0794787, 0. 132354, 0. 364311, -0. 0990995, -0. 0794787, -0. 0855786, -0. 094433, 0. 0464288, -0. 140719, 0. 0526153, -0. 0746189, 0. 418075, …. 58

Possible pretest : measure of predictability of the financial time-series Actual question : how predictable for a given horizon with a given cost function? n § § § Serial correlation Kolmogorov complexity Lyapunov exponent Unit root analysis Comparison with results on surrogate data : “shuffled” series (e. g. Kaboudan statistics) . . . 59

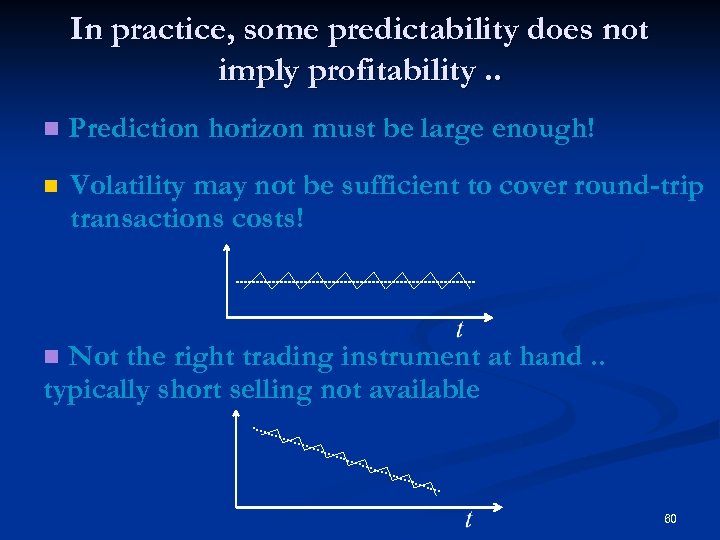In practice, some predictability does not imply profitability. . n Prediction horizon must be large enough! n Volatility may not be sufficient to cover round-trip transactions costs! Not the right trading instrument at hand. . typically short selling not available n 60

Pretest methodology n Compare GP with several variants of n Random è “Zero-Intelligence Strategies” - ZIS n Random è search algorithms trading behaviors “Lottery trading” - LT Issue : how to best constrain randomness ? n Statistical hypotheses testing n Null : GP does not outperform ZIS n Null : GP does not outperform LT 61

Pretest 1 : GP versus Zero-Intelligence strategies (=“Equivalent search intensity” Random Search (ERS) with validation stage) -Null hypothesis H 1, 0 : GP does not outperform equivalent random search - Alternative hypothesis is H 1, 1

Pretest 1 : GP vs zero-intelligence strategies Training interval 1 ) Creation of the trading rules using GP ERS 2) Selection of the best resulting strategies n Validation interval Further selection on unseen data Out-of-sample interval Performance evaluation One strategy is chosen for out-of-sample H 1, 0 cannot be rejected – interpretation : è There is nothing to learn or GP is not very effective 63

Pretest 4 : GP vs lottery trading n Lottery trading (LT) = random trading behavior according the outcome of a r. v. (e. g. Bernoulli law) n n Issue 1 : if LT tends to hold positions (short, long) for less time that GP, transactions costs may advantage GP. . Issue 2 : it might be an advantage or an disadvantage for LT to trade much less or much more than GP. è ex: downward oriented market with no short-sell 64

Frequency and intensity of a trading strategy n Frequency : average number of transactions per unit of time n n Intensity : proportion of time where a position is held For pretest 4 : We impose that average frequency and intensity of LT is equal to the ones of GP è Implementation : generate random trading sequences having the right characteristics è 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, … 65

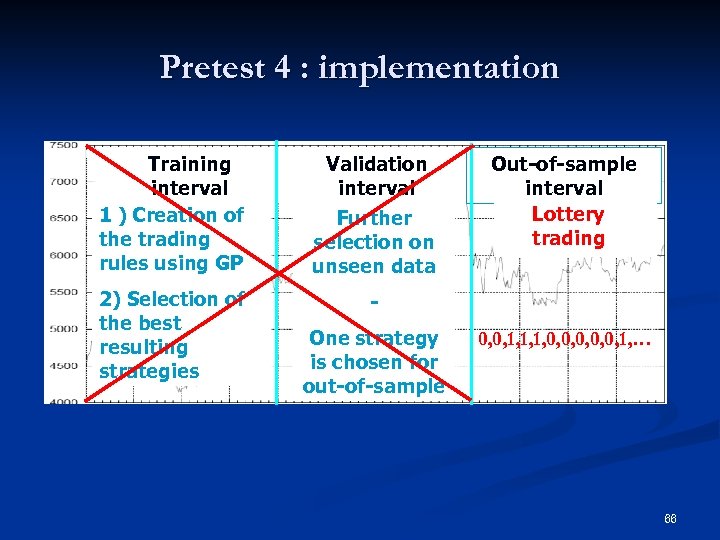Pretest 4 : implementation Training interval 1 ) Creation of the trading rules using GP 2) Selection of the best resulting strategies Validation interval Further selection on unseen data Out-of-sample interval Lottery Performance trading evaluation One strategy is chosen for out-of-sample 0, 0, 1, 1, 1, 0, 0, 0, 1, … 66

Answering question 1 : is there anything to learn on the training data at hand ?

Question 1 : pretests involved n n Starting point: if a set of search algorithms do not outperform LT, it gives evidence that there is nothing to learn. . Pretest 4 : GP vs Lottery Trading è Null n hypothesis H 4, 0 : GP does not outperform LT Pretest 5 : Equivalent Random Search (ZIS) vs Lottery Trading è Null hypothesis H 5, 0 : ERS does not outperform LT 68

Question 1 : some answers. . . n R means that the null hypothesis Hi, 0 cannot be rejected – R means we should favor Hi, 1 H 4, 0 H 5, 0 Case 1 Case 2 Case 3 R R R Case 4 R R Interpretation there is nothing to learn there is something to learn there may be something to learn ERS might not be powerful enough there may be something to learn – GP evolution process is detrimental 69

Answering question 2 : is GP effective ?

Question 2 : some answers. . . n n n Question 2 cannot be answered if there is nothing to learn (case 1) Case 4 provides us with a negative answer. . In case 2 and 3, run pretest 1 : GP vs Equivalent random search Null hypothesis H 1, 0 : GP does not outperform ERS n If one cannot reject H 1, 0 GP shows no evidence of efficiency… n 71

Pretests at work Methodology : Draw conclusions from pretests using our own programs and compare with results in the literature [Ch. Ku. Ho 06] on the same time series

Setup : GP control parameters - same as in [Ch. Ku. Ho 06] 73

Setup : statistics, data, trading scheme n n n n Hypothesis testing with student t-test with a 95% confidence level Pretests with samples made of 50 GP runs, 50 ERS runs and 100 LT runs Data : indexes of 3 stock exchanges Canada, Taiwan and Japan Daily trading with short selling Training of 3 years – Validation of 2 years Out-of-sample periods: 1999 -2000, 2001 -2002, 2003 -2004 Data normalized with a 250 days moving average 74

Results on actual data (1/2) § Evidence that there is something to learn : 4 markets out of 9 (C 3, J 2, T 1, T 3) è Experiments in [Ch. Ku. Ho 06], with another GP implementation, show that GP performs very well on these 4 markets § Evidence that there is nothing to learn : 3 (C 1, J 3, T 2) è In [Ch. Ku. Ho 06], there is only one (C 1) where GP has positive return (but less than B&H) 75

Results on actual data (2/2) n GP effective : 3 markets out of 6 è n In these 3 markets, GP outperforms Buy and Hold – same outcome as in [Ch. Ku. Ho 06] Preliminary conclusion : one can rely on pretests. . è When there is nothing to learn, no GP implementation did good (except in one case) è When there is something to learn, at least one implementation did good (always) è When our GP is effective, GP in [Ch. Ku. Ho 06] is effective too (always) 76

Further conclusion n Our GP implementation is 1. is more efficient than random search : no case where ERS outperform LT and GP did not 2. But only slightly more efficient … one would expect much more cases where GP does better than LT and not ERS n Our GP is actually able to take advantage of regularities in data … but only of “simple” ones 77

Part 4 : Perspectives in the field of GP for financial trading

Rethinking fitness functions From [La. Po 02] Fitness functions : accumulated return, riskadjusted return, … n Issue : on some problems [La. Po 02], GP is only marginally better than random search because fitness function induces a “difficult" landscape … è Come up with GP-friendly fitness functions … n 79

Preprocessing of the data : still an open issue n Studies in forecasting show the importance of preprocessing – for GP, often, normalization with MA(250) is used - with benefits [Ch. Ku. Ho 06] Length of MA should change according to markets volatility, regime changes, etc ? è Why not consider : MACD, Exponential MA, differencing, rate of change, log value, FFT, wavelet, … è 80

Data division scheme There is evidence that GP performs poorly when the characteristics of the training interval are very different from the out-ofsample interval … n Characterization of the current market condition : mean reverting, trend following. . . n Relearning on a smaller interval if needed ? n 81

More extensive tests are needed. . automating the test A comprehensive test for daily indexes done in [Ch. Ku. Ho 06], none exists for individual stocks and intraday data … è Automated testing on several hundred of stocks is fully feasible … but require a software infrastructure and much computing power n 82

Ensemble methods : combining trading rules In ML, ensemble methods have proven to be very effective n Majority rule tested in [Ch. Ku. Ho 06] with some success è Efficiency requirement : accuracy (better than random) and diversity (uncorrelated errors) – what does it mean for trading rules? è More fine grained selection / weighting scheme may lead to better results … n 83

Embed more domain specific knowledge Black-box algorithms are usually outperformed by domain-specific algorithms n Domain-specific language is limited as yet … è Enrich primitive set with volume, indexes, bid/ask spread, … è Enrich function set with cross-correlation, predictability measure, … n 84

References (1/2) n n n n [Ch. Ku. Ho 06] S. -H. Chen and T. -W. Kuo and K. -M. Hoi. “Genetic Programming and Financial Trading: How Much about "What we Know“”. In 4 th NTU International Conference on Economics, Finance and Accounting, April 2006. [Ch. Na 06] S. -H. Chen and N. Navet. “Pretests for genetic-programming evolved trading programs : “zero-intelligence” strategies and lottery trading”, Proc. ICONIP’ 2006. [Si. Al 03] S. Silva and J. Almeida, “Dynamic Maximum Tree Depth - A Simple Technique for Avoiding Bloat in Tree-Based GP”, GECCO 2003, LNCS 2724, pp. 1776– 1787, 2003. [Str 03] M. J. Streeter, “The Root Causes of Code Growth in Genetic Programming”, Euro. GP 2003, pp. 443 - 454, 2003. [Te. He 04] M. D. Terrio, M. I. Heywood, “On Naïve Crossover Biases with Reproduction for Simple Solutions to Classification Problems”, GECCO 2004, 2004. [Zu. Pi. Ma 01] G. Zumbach, O. V. Pictet, and O. Masutti, “Genetic Programming with Syntactic Restrictions applied to Financial Volatility Forecasting”, Olsen & Associates, Research Report, 2001. [Ev. Fe 98] M. Evett, T. Fernandez, “Numeric Mutation Improves the Discovery of Numeric Constants in Genetic Programming”, Genetic Programming 1998: Proceedings of the Third Annual Conference, 1998. 85

References (2/2) n n n n [Kab 02] M. Kaboudan, “GP Forecasts of Stock Prices for Profitable Trading”, Evolutionary computation in economics and finance, 2002. [Sa. Te 02] M. Santini, A. Tettamanzi, “Genetic Programming for Financial Series Prediction”, Proceedings of Euro. GP'2001, 2001. [Bh. Pi. Zu 02] S. Bhattacharyya, O. V. Pictet, G. Zumbach, “Knowledge-Intensive Genetic Discovery in Foreign Exchange Markets”, IEEE Transactions on Evolutionary Computation, vol 6, n° 2, April 2002. [La. Po 02] W. B. Langdon, R. Poli, “Fondations of Genetic Programming”, Springer Verlag, 2002. [Kab 00] M. Kaboudan, “Genetic Programming Prediction of Stock Prices”, Computational Economics, vol 16, 2000. [Wag 03] L. Wagman, “Stock Portfolio Evaluation: An Application of Genetic. Programming-Based Technical Analysis”, Genetic Algorithms and Genetic Programming at Stanford 2003, 2003. [Go. Fe 99] W. Golubski and T. Feuring, “Evolving Neural Network Structures by Means of Genetic Programming”, Proceedings of Euro. GP'99, 1999. [Dem 05] I. Dempsey, “Constant Generation for the Financial Domain using Grammatical Evolution”, Proceedings of the 2005 workshops on Genetic and evolutionary computation 2005, pp 350 – 353, Washington, June 25 - 26, 2005. 86

? 87