Генераторы случайных чисел Вероятность Случайные величины с

Генераторы случайных чисел

Вероятность. Случайные величины с дискретным и непрерывным распределением Получение и тестирование случайных чисел Преобразование случайных величин

Несколько определений • События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. • Несколько событий образуют полную группу событий, если в результате каждого испытания происходит хотя бы одно из них. • События образуют полную группу, попарно несовместных событий, если в результате испытания появится одно и только одно из эти событий.

Непрерывная и дискретные случайные величины Случайная величина называется дискретной, если принимаемые ею значения можно пронумеровать Непрерывная случайная величина задаётся интервалом, содержащим возможные значения этой величины, и плотностью распределения вероятности, которая определяется следующим соотношением: Здесь – (a’, b’) интервал, содержащийся внутри; P (a’<ξ

Генератор случайных чисел должен удовлетворять набору жёстких требований: Удовлетворять статистическим тестам Иметь как можно более длинный период Работать как можно быстрее Воспроизводить одну последовательность чисел необходимое число раз Получать одну и ту же последовательность на разных компьютерах.

Получение случайных чисел Идея линейного конгруэнтного метода: Xn+1={ G(Xn) }

Получение случайных чисел Линейный конгруэнтный метод Где а – множитель с – сдвиг m – модуль mod – операция взятия остатка от деления – начальное значение, «затравка» (seed) Свойства: • последовательность периодична с периодом, не превышающим m • все элементы этой последовательности однозначно определяются четырьмя параметрами: x 0, a, c, m • числа последовательности xn удовлетворяют неравенству xn < m • последовательность чисел yn, равномерно распределенных в интервале (0; 1), получается по формуле

Линейный конгруэнтный метод Преимущества: • быстрота, за счет малого количества операций на байт • простота реализации Недостатки: • предсказуемы • короткий период • некоторые биты «менее случайны» , чем другие (обычно это младшие двоичные разряды)

Генератор Лемера (Lehmer) Наиболее популярные: MINSTD (Park–Miller) a = 75 = 16 807 m = 231 -1 = 2 147 483 647 RANF a = 75 m = 216 -1 = 65 537 RANDU a = 65539 m = 231 = 2 147 483 648

Минимальный генератор Парка‑Миллера (Miller “Minimal Standard” generator - MINSTD) • • • Не имеет сдвига Не требует отсечения «плохих» битов Простота Хорошее быстродействие Хорошее равномерное распределение

Алгоритм Шраге (Schrage) При программной реализации MINSTD для корректного умножения двух 32 -битных чисел по модулю 32 -битного числа без переполнения 32 -битной переменной использовался алгоритм Шраге. Модуль разлагается в выражение: m=a*q+r Если r

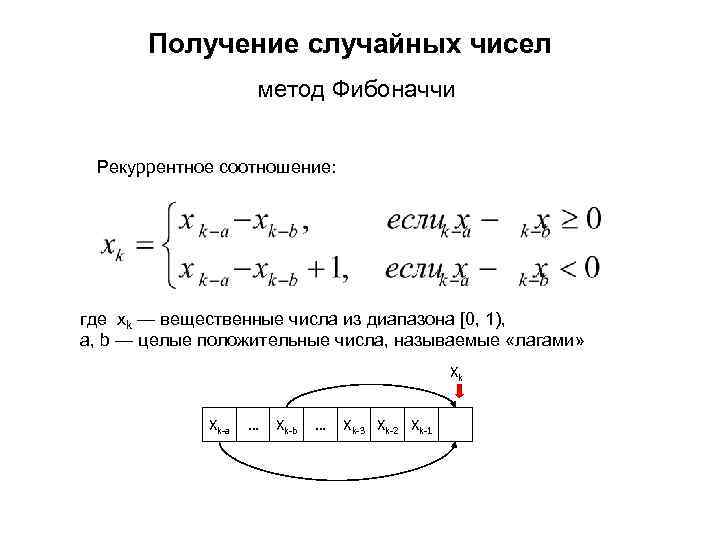Получение случайных чисел метод Фибоначчи Рекуррентное соотношение: где xk — вещественные числа из диапазона [0, 1), a, b — целые положительные числа, называемые «лагами» Xk Xk-a … Xk-b … Xk-3 Xk-2 Xk-1

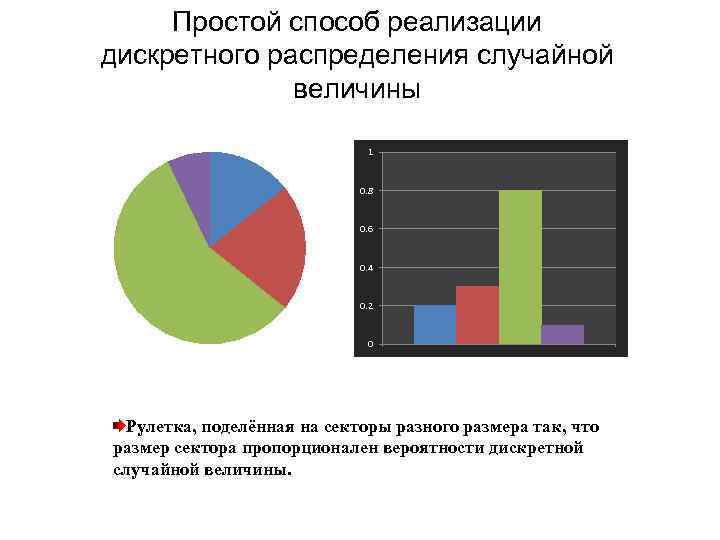Простой способ реализации дискретного распределения случайной величины 1 0. 8 0. 6 0. 4 0. 2 0 Рулетка, поделённая на секторы разного размера так, что размер сектора пропорционален вероятности дискретной случайной величины.

Разыгрывание непрерывной случайной величины с произвольной плотностью распределения Чтобы получить распределение с заданной плотностью p(x) на интервале ( a; b) необходимо решить уравнение где y - число из равномерного распределения на интервале (0; 1). Пример: экспоненциальное распределения на интервале (0; x) что распределено также, как и

Получение приближённого нормального распределения Чтобы разыграть возможное значение нормальной случайной величины с параметрами σ=1 и а=0, надо сложить 12 случайных чисел из равномерного распределения на интервале (0, 1) и из полученной суммы вычесть 6.