Generating Test Data for Killing SQL Mutants A

Generating Test Data for Killing SQL Mutants: A Constraint Based Approach Shetal Shah, S. Sudarshan, Suhas Kajbaje, Sandeep Patidar Bhanu Pratap Gupta, Devang Vira CSE Department, IIT Bombay ICDE 2011 1

Testing SQL Queries: A Challenge l l Complex SQL queries hard to get right Question: How to check if an SQL query is correct? l l Formal verification is not applicable since we do not have a separate specification and an implementation State of the art solution: manually generate test databases and check if the query gives the intended result l Often misses errors ICDE 2011 2

Example l Find number of high paid instructors in each department deptname. Gcount(instr. ID) σ sal>100000 dept σ sal>100000 instructor dept instructor Problem: does not output departments with no high paid instructors Test dataset should be able to distinguish these two alternatives ICDE 2011 3

Generating Test Data: Prior Work l Automated Test Data generation l l Initial work based on database constraints alone Later work: DB constraints + SQL query l Agenda, Reverse Query Processing (RQP), QAGen l Our earlier work in ICDE 2010 (poster) on killing SQL mutants l More recent (independent) de la Riva et al [AST 10] consider test data generation for killing mutants § l l l But limited space of mutations, no guarantees of completeness None of the above guarantee anything about detecting errors in SQL queries Question: How do you model SQL errors? Answer: Query Mutation ICDE 2011 4

Query Mutations l Mutations: model common programming errors l l Join used instead of outerjoin (or vice versa) Join/selection condition errors § l l l Wrong aggregate (min vs. max) Mutant: syntactic variation of the given query Q l l < vs. <=, missing or extra condition Mutant may be the intended query A dataset D kills a mutant M of query Q if output of Q and M differ on D For a mutation space, a dataset suite is complete if all non-equivalent mutants are killed ICDE 2011 5

Mutation Testing of Queries l Mutation testing can be used to check coverage of a test suite l l Given a test suite, generate mutants in a pre-defined mutation space; evaluate on a given test suite Our goal is different: l l l Generate datasets for the given query, based on possible mutations Each dataset and query result on the dataset shown to a human, who verifies that the query result is what is expected on that dataset We do not need to actually generate and execute mutants ICDE 2011 6

Query and Mutation Space Query: Single Block SQL Query with unconstrained aggregation at the top Mutation Space: l Join Type Mutation : change of any of inner join, left outer join, right outer join, full outer join to another l l l Across all possible join orders (unlike earlier work) Comparison Operator Mutations: An occurrence of one of (=, <, >, <=, >=, <>) in the WHERE clause replaced by another Unconstrained Aggregation Mutations: l MIN ↔ MAX, SUM ↔ SUM(DISTINCT) AVG ↔ AVG(DISTINCT), COUNT ↔ COUNT(DISTINCT) ICDE 2011 7

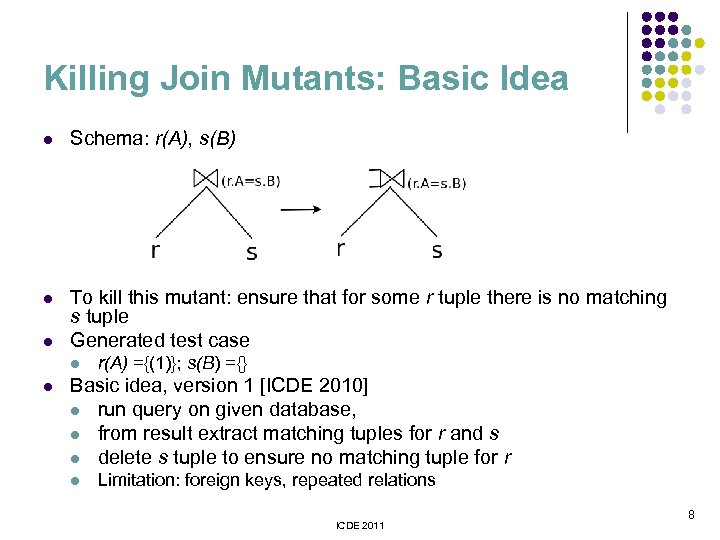Killing Join Mutants: Basic Idea l Schema: r(A), s(B) l To kill this mutant: ensure that for some r tuple there is no matching s tuple Generated test case l l l r(A) ={(1)}; s(B) ={} Basic idea, version 1 [ICDE 2010] l run query on given database, l from result extract matching tuples for r and s l delete s tuple to ensure no matching tuple for r l Limitation: foreign keys, repeated relations ICDE 2011 8

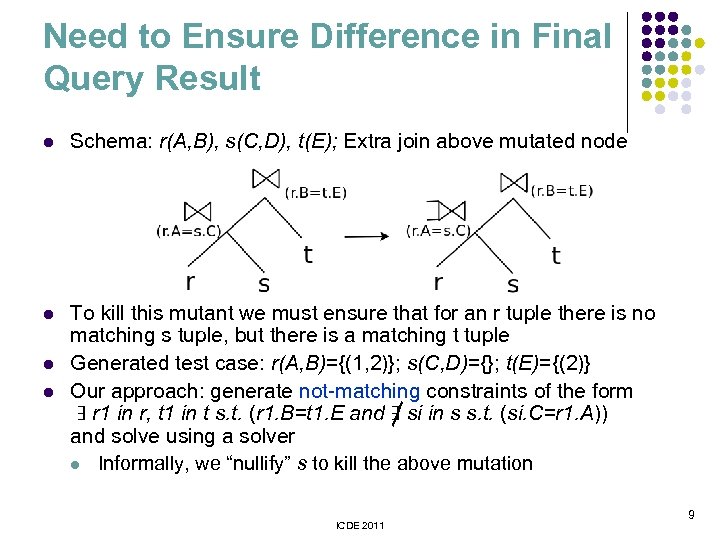Need to Ensure Difference in Final Query Result l Schema: r(A, B), s(C, D), t(E); Extra join above mutated node l To kill this mutant we must ensure that for an r tuple there is no matching s tuple, but there is a matching t tuple Generated test case: r(A, B)={(1, 2)}; s(C, D)={}; t(E)={(2)} Our approach: generate not-matching constraints of the form ∃ r 1 in r, t 1 in t s. t. (r 1. B=t 1. E and ∃ si in s s. t. (si. C=r 1. A)) and solve using a solver l Informally, we “nullify” s to kill the above mutation l l ICDE 2011 9

Working around Foreign Key Constraints l l teaches instructor is equivalent to teaches instructor if there is a foreign key from teaches. ID to instructor. ID BUT: teaches σ dept=CS(instructor) is not equivalent to teaches σ dept=CS(instructor) Key idea: have a teaches tuple with an instructor not from CS Selections and joins can be used to kill mutations l We show that it comes for free when we “nullify” relations to kill other join mutations or generate data to kill selection mutations ICDE 2011 10

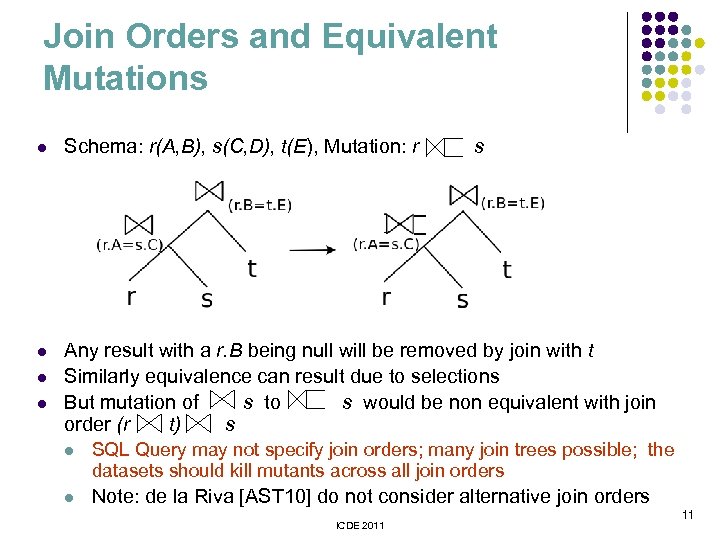Join Orders and Equivalent Mutations l Schema: r(A, B), s(C, D), t(E), Mutation: r l Any result with a r. B being null will be removed by join with t Similarly equivalence can result due to selections But mutation of s to s would be non equivalent with join order (r t) s l l s l SQL Query may not specify join orders; many join trees possible; the datasets should kill mutants across all join orders l Note: de la Riva [AST 10] do not consider alternative join orders ICDE 2011 11

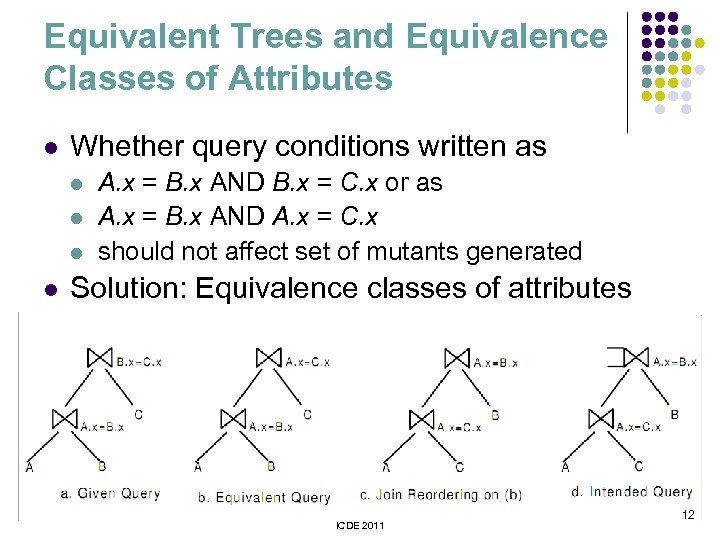Equivalent Trees and Equivalence Classes of Attributes l Whether query conditions written as l l A. x = B. x AND B. x = C. x or as A. x = B. x AND A. x = C. x should not affect set of mutants generated Solution: Equivalence classes of attributes ICDE 2011 12

Data Generation Algorithm Assumptions l Only PK/FK constraints, single block SQL queries, only simple arithmetic expressions, predicates are purely conjunctive (and a few more in paper) l Algorithm Overview l For each dataset generate constraints. l 1. 2. 3. DB constraints : primary key, foreign key constraints Query constraints: join conditions, selection conditions, other than conditions inconsistent with non-matching constraints (see below) Constraints to kill mutations: not-matching constraints derived from join/selection conditions l One constraint per dataset Generate Test Data l 1. Using a constraint solver (currently CVC 3) on above constraints ICDE 2011 13

Main Procedure: generate. Data. Set(query q) l preprocess query tree l l l build equivalence classes foreign key closure generate. Data. Set. For. Original. Query() A constraint set with only DB and Query constraints such that the result set for q is non-empty l l kill. Equivalence. Classes() kill. Other. Predicates() kill. Comparison. Operators() kill. Aggregates() ICDE 2011 14

Killing Join Mutants: Equijoin (kill. Equivalence. Classes) l Query : r l l l t where r. A = s. B and s. B =t. C r. A, s. B, t. C are in one equivalence class Generate one dataset for each element of each equivalence class Three datasets generated, with not-matching mutation constraints: l l s D 1: ∃r 1εr ∃s 1εs (r 1. A = s 1. B ∧ ∃tiεt (ti. C=r 1. A)) D 2: ∃s 1εs ∃t 1εt (s 1. B = t 1. C ∧ ∃riεr (ri. A=s 1. B)) D 3: ∃r 1εr ∃t 1εt (r 1. A = t 1. C ∧ ∃siεs (si. B=t 1. C)) But if t. C is an FK referencing s. B, instead generate l D 3’: ∃r 1εr (∃tiεt, siεs (si. B=r 1. A ∧ ti. C=r 1. A)) ICDE 2011 15

Comparison Operation Mutations l l l Example of comparison operation mutations: A < 5 vs. A <= 5 vs. A > 5 vs A >= 5 vs. A=5, vs A <> 5 Idea: generate three datasets (leaving rest of query unchanged), one each for: l l A<5 A=5 A>5 These datasets will kill above mutations ICDE 2011 16

Aggregation Operation Mutations l l l Aggregation operations l count(A) ↔ count(distinct A); sum(A) ↔ sum(distinct A) l avg(A) ↔ avg(distinct A); min(A) ↔ max(A) Eg: select min (salary) from instructor group by dept_name; Dataset Generated: [CS, Srinivasan, 80000] One group with two values equal (and <> 0), [CS, Wu, 80000] Third different [CS, Alex, 65000] will kill each of the above pairs of mutations Issues: l Database/query constraints forcing A to be unique l Database/query constraints forcing G to be unique Carefully crafted set of constraints, which are relaxed to handle such cases l Details in paper ICDE 2011 17

On Completeness and Complexity l l With respect to query size: l Number of datasets generated: linear l Number of mutants: exponential Theorem: The problem of generating data to kill a mutant is NPhard l reduction from query containment; polynomial in special cases. Theorem: For the class of queries, and the space of join-type and selection mutations considered, the suite of datasets generated by our algorithm is complete, i. e. , the datasets kill all non-equivalent mutations of a given query Also complete for a restricted classes of aggregation mutations with aggregation as top operation of tree, under some restrictions on joins in input ICDE 2011 18

Performance Results l l University database schema from Database System Concepts 6 th Ed consisting of 7 relations Further Optimizations : Unfolding of bounded first order quantified constraints l l E. g. “for all i in 1 to 4, P(i)” unfolded as P(1) ∧ P(2) ∧ P(3) ∧ P(4) Also tested with addition of input database constraints l Forcing output tuples to come from input database ICDE 2011 19

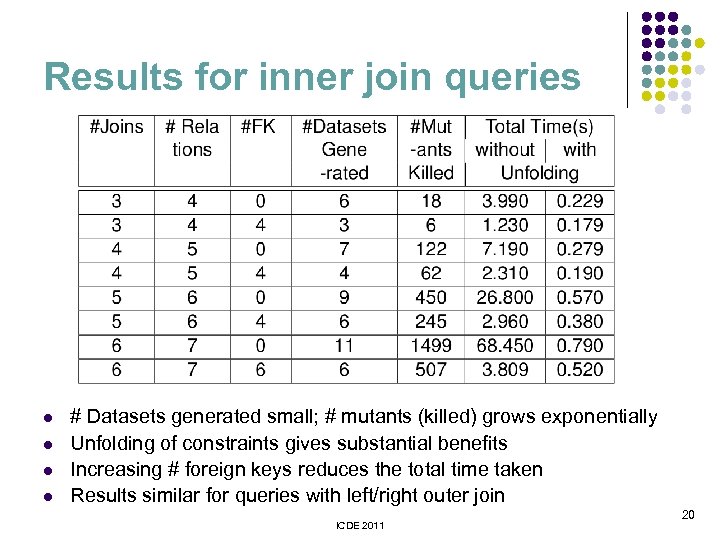Results for inner join queries l l # Datasets generated small; # mutants (killed) grows exponentially Unfolding of constraints gives substantial benefits Increasing # foreign keys reduces the total time taken Results similar for queries with left/right outer join ICDE 2011 20

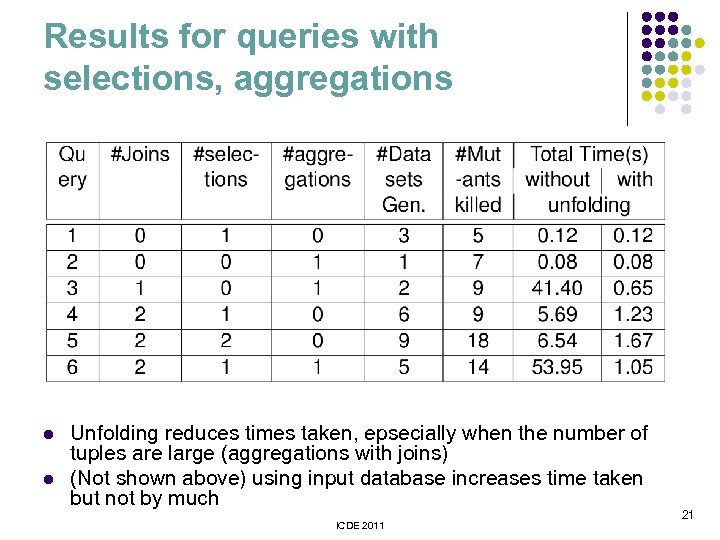Results for queries with selections, aggregations l l Unfolding reduces times taken, epsecially when the number of tuples are large (aggregations with joins) (Not shown above) using input database increases time taken but not by much ICDE 2011 21

Conclusions and Future Work l Presented a principled approach to data generation for testing queries l l We’ve only made first steps; more work to be done: l l l And showed it works efficiently for a large class of queries Constrained aggregations and sub-queries Other mutations: e. g. , missing/extra join and selection conditions Multiple queries Query and form parameters Acknowledgements l l Bhupesh Chawda for discussions/implementation help Microsoft Research India for their generous travel support ICDE 2011 22

Questions Thank You ICDE 2011 23

Related Work l l l Tuya and Suarez-Cabal [IST 07], Chan et al. [QSIC 05] defined a class of SQL query mutations Shortcoming: do not address test data generation More recently (and independent of our work) de la Riva et al [AST 10] address data generation using constraints, with the Alloy solver l Do not consider alternative join orders, No completeness results, Limitations on constraints ICDE 2011 24

Dataset for Original Query l l l Array of tuples of constraint variables, per relation One or more constraint tuple from array, for each occurrence of a relation l plus occurrences to ensure f. k. constraints Equality conditions between variables based on equijoins Other selection and join conditions become constraints Constraints for primary and foreign keys l f. k. from R. A to S. B l l p. k. on R. A l l l FORALL i EXISTS j (O_R[i]. A = O_S[j]. B); FORALL i FORALL j (O_R[i]. A = O_R[j]. A]) => “all other attrs equal” since range is over finite domain, p. k. and f. k. constraints can be unfolded See sample set of constraints in file cvc 3_0. cvc ICDE 2011 25

Killing Join Mutants: Equijoin l l kill. Equivalence. Classes() for each equivalence class ec do l l Let all. Relations : = Set of all pairs in ec for each element e in all. Relations do l conds : = empty set l Let e : = R. a l S : = (set of elements in ec which are foreign keys referencing R. a directly or indirectly) UNION R: a l P : = ec - S l if P: is. Empty() then § l continue else … main code for generating constraints (see next slide) ICDE 2011 26

Killing Join Mutants: Equi. Joins l l conds. add(generate. Eq. Conds(P)) conds: add( “NOT EXISTS i: R[i]. a = ” + cvc. Map(P[0])) for all other equivalence classes oe do l l for each other predicate p do l l conds. add(generate. Eq. Conds(oe)) conds: add(cvc. Map(p)) conds. add(gen. DBConstraints()) /*P. K. and F. K*/ call. Solver(conds) if solution exists then l create a dataset from solver output ICDE 2011 27

Killing Other Predicates l l Create separate dataset for each attribute in predicate e. g. For Join condition B. x = C. x + 10 l Dataset 1 (nullifying B: x): l l ASSERT NOT EXISTS (i : B_INT) : (B[i]. x = C[1]. x + 10); Dataset 2 (nullifying C: x): l ASSERT NOT EXISTS (i : C_INT) : (B[1]. x = C[i]. x + 10); ICDE 2011 28