Generating minimum transitivity constraints in P-time for deciding

Generating minimum transitivity constraints in P-time for deciding Equality Logic Ofer Strichman and Mirron Rozanov Technion, Haifa, Israel Technion 1

Deciding Equality Logic (TE) n The eager approach: TE ! Pr n Bryant & Velev [BV-CAV’ 00] – Boolean satisfiability with transitivity constraints. Meir and Strichman [MS-CAV’ 05] – Yet another decision procedure for equality logic. n n This work: a ‘closure’ on [MS-CAV’ 05] Technion 2

Basic notions E: x = y Æ y = z Æ z x (non-polar) Equality Graph: y x z Technion 3

From Equality to Propositional Logic E : x 1 = x 2 Æ x 2 = x 3 Æ x 1 x 3 sk : e 1, 2 Æ e 2, 3 Æ : e 1, 3 x 1 e 1 , 2 e 1, 3 [BV-CAV'00] – the Sparse method x 2 e 2, 3 x 3 n Encode all edges with Boolean variables n Add transitivity constraints Technion 4

From Equality to Propositional Logic E : x 1 = x 2 Æ x 2 = x 3 Æ x 1 x 3 sk : e 1, 2 Æ e 2, 3 Æ : e 1, 3 x 1 e 1 , 2 e 1, 3 [BV-CAV'00] – the Sparse method x 2 e 2, 3 x 3 n Transitivity Constraints: For each cycle of size n, forbid a true assignment to n-1 edges T S = (e 1, 2 Æ e 2, 3 ! e 1, 3) Æ (e 1, 2 Æ e 1, 3 ! e 2, 3) Æ (e 1, 3 Æ e 2, 3 ! e 1, 2) Check: sk Æ T S Technion 5

From Equality to Propositional Logic [BV-CAV'00] – the Sparse method n Thm-1: It is sufficient to constrain chord-free simple cycles e 2 e 1 e 5 e 3 e 4 n There can be an exponential number of chord-free simple cycles… Technion 6

From Equality to Propositional Logic [BV-CAV'00] – the Sparse method n Make the graph ‘chordal’. n In a chordal graph, it is sufficient to constrain only triangles. n Polynomial # of edges and constraints. n # constraints = 3 £ #triangles Technion 7

An improvement [MS-CAV’ 05] – the RTC method n So far we did not consider the polarity of the edges. E: x = y Æ y = z Æ z x n Assuming E is in Negation Normal Form y (polar) Equality Graph: x = = Technion z 8

An improvement Reduced Transitivity Constraints (RTC) n Here, T R = e 3 Æ e 2 ! e 1 is sufficient z T F Allowing e. g. : x = z, x = y, z y T e 3 e 1 ’: x = z, x = y, z = y = x n T e 2 = y This is only true because of monotonicity of NNF Technion 9

Definitions n Dfn-1: A contradictory cycle is a cycle with exactly one disequality edge. T T C= T T n F Dfn-2: A contradictory Cycle C is constrained under T if T does not allow such an assignment. Technion 10

Main theorem [MS-CAV’ 05] n Let T R be a conjunction of transitivity constraints. n If T R constrains all simple contradictory cycles then E is satisfiable iff sk Æ T R is satisfiable The Equality Formula Technion 11

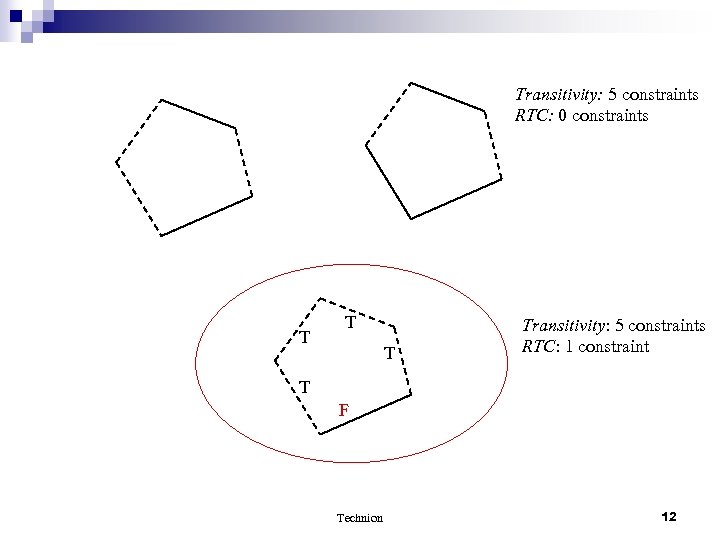Transitivity: 5 constraints RTC: 0 constraints T Transitivity: 5 constraints RTC: 1 constraint T F Technion 12

Applying RTC n How can we use theorem without enumerating contradictory cycles ? n Answer: ¨ Consider the chordal graph. ¨ Still – which triangles ? which constraints? Technion 14

The RTC solution [MS-CAV’ 05] x 2 x 0 x 4 cache: e 0, 2 Æ e 1, 2 e e 0, 1 Æ e e 1, 3 2, 3 1, 2 e 2, 4 Æ e 3, 4 e 2, 3 e 0, 2 Æ e 0, 4 e 2, 4 x 1 n x 3 1) Exp # cycles to traverse 2) Not all cycles are simple. Solution to 1): Stop before adding an existing constraint ¨ Solution to 2): Explore only simple cycles ¨ n These solutions cannot be combined. Technion 15

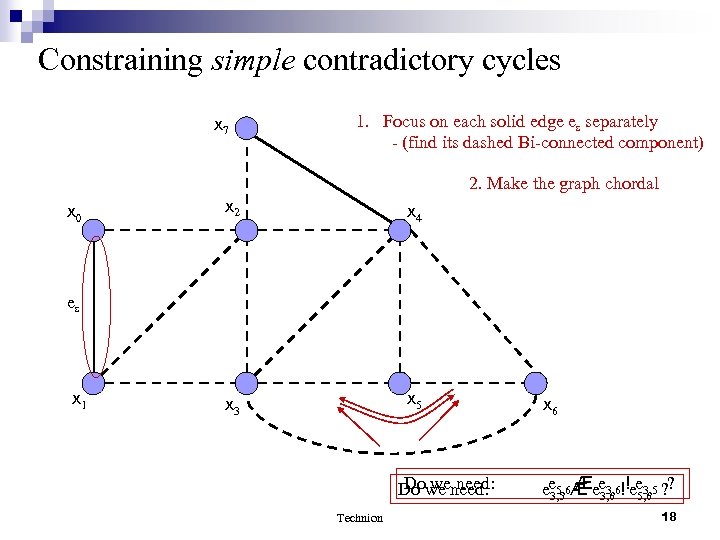Constraining simple contradictory cycles x 7 1. Focus on each solid edge es separately - (find its dashed Bi-connected component) 2. Make the graph chordal x 0 x 2 x 4 x 3 x 5 es x 1 Do we need: Technion x 6 Æ ee 5, 6Æ ee 3, 6! !ee 3, 5 ? ? 3, 5 3, 6 5, 6 18

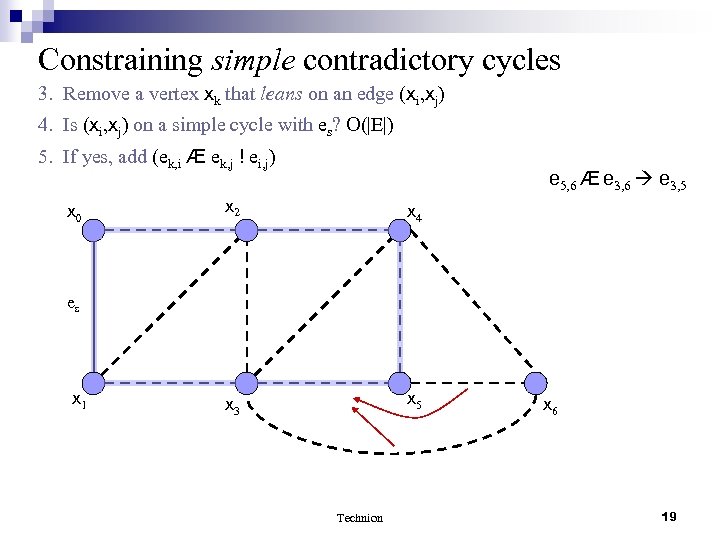Constraining simple contradictory cycles 3. Remove a vertex xk that leans on an edge (xi, xj) 4. Is (xi, xj) on a simple cycle with es? O(|E|) 5. If yes, add (ek, i Æ ek, j ! ei, j) x 0 e 5, 6 Æ e 3, 6 e 3, 5 x 2 x 4 x 3 x 5 es x 1 Technion x 6 19

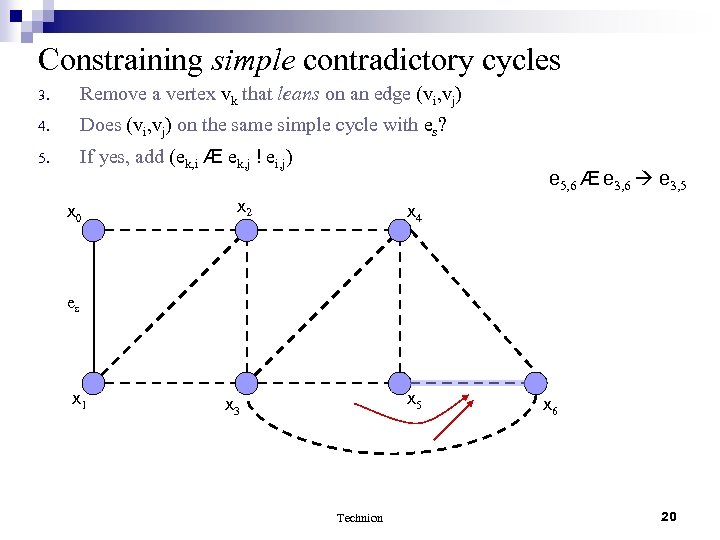Constraining simple contradictory cycles 3. Remove a vertex vk that leans on an edge (vi, vj) 4. Does (vi, vj) on the same simple cycle with es? 5. If yes, add (ek, i Æ ek, j ! ei, j) x 0 e 5, 6 Æ e 3, 6 e 3, 5 x 2 x 4 es x 1 x 5 x 3 Technion x 6 20

Correctness n The set of generated constraints is sufficient. n The set of generated constraints is necessary. Technion 21

Random graphs (Satisfiable) [MS-CAV’ 05] Technion 22

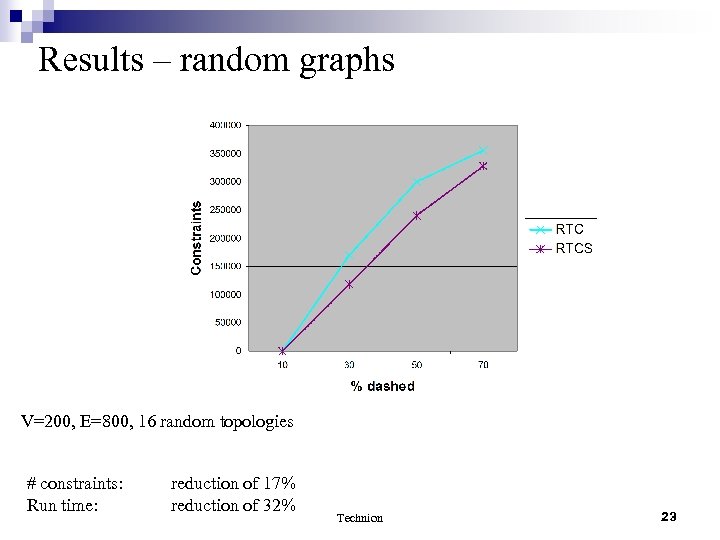Results – random graphs V=200, E=800, 16 random topologies # constraints: Run time: reduction of 17% reduction of 32% Technion 23

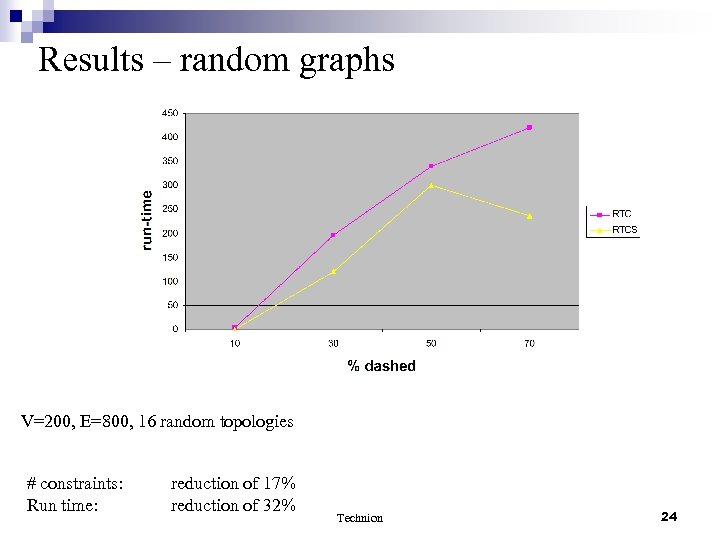Results – random graphs V=200, E=800, 16 random topologies # constraints: Run time: reduction of 17% reduction of 32% Technion 24

SMT benchmarks n Never really finished the implementation… n Our 4 -5 experiments with them showed that We still have a small advantage comparing to the Sparse method. ¨ Yet Yices is much better…. ¨ A result of the Uninterpreted functions. ¨ n Are there formulas for which the eager approach still wins? n Generating meaningful equality formulas is hard… Technion 25

A crafted example 2 n assignments satisfy sk. None satisfy theory. Technion 26

Thank you Technion 27

Results Uclid benchmarks* (all unsat) * Results strongly depend on the reduction method of Uninterpreted Functions. Technion 28

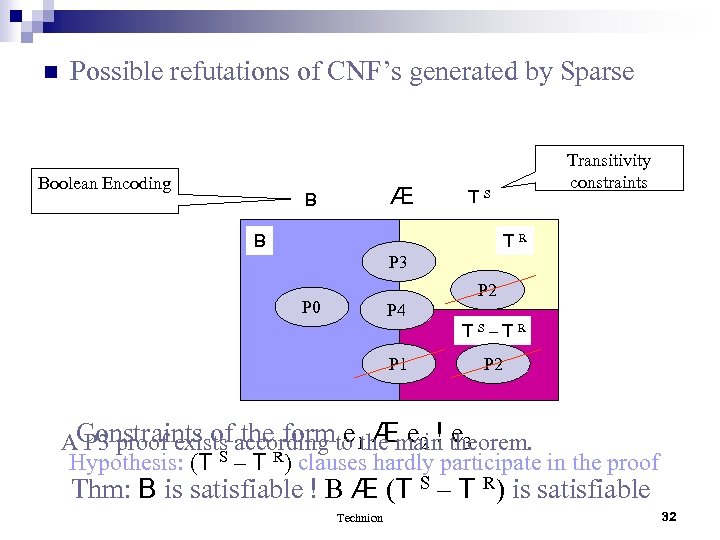n Possible refutations of CNF’s generated by Sparse Boolean Encoding Æ B Transitivity constraints TS B TR P 3 P 2 P 0 P 4 TS–TR P 1 P 2 AConstraints ofaccording to 1 Æ e 2 ! theorem. P 3 proof exists the form e the main e 3 Hypothesis: (T S – T R) clauses hardly participate in the proof Thm: B is satisfiable ! B Æ (T S – T R) is satisfiable Technion 32

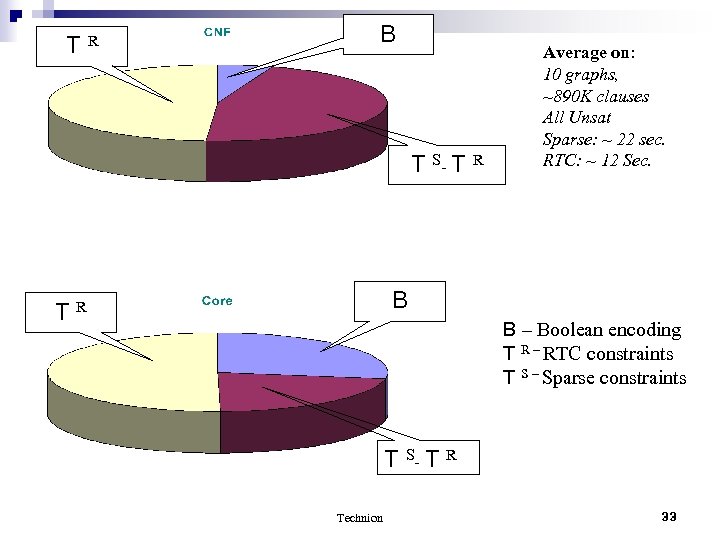TR B T S- T R Average on: 10 graphs, ~890 K clauses All Unsat Sparse: ~ 22 sec. RTC: ~ 12 Sec. B TR B – Boolean encoding T R – RTC constraints T S – Sparse constraints T S- T R Technion 33

Summary n The RTC method is ~dominant over the Sparse method. n Open issue: find a P-time algorithm that exploits the full power of the main theorem. Technion 34

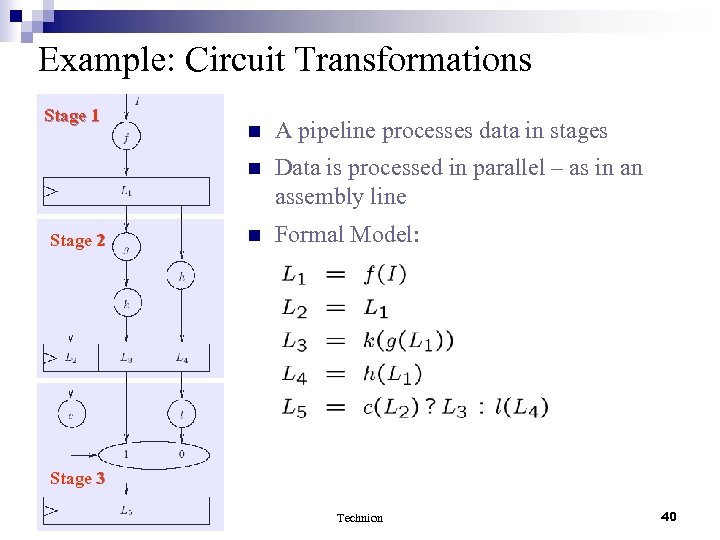Example: Circuit Transformations Stage 1 A pipeline processes data in stages n Stage 2 n Data is processed in parallel – as in an assembly line n Formal Model: Stage 3 Technion 40

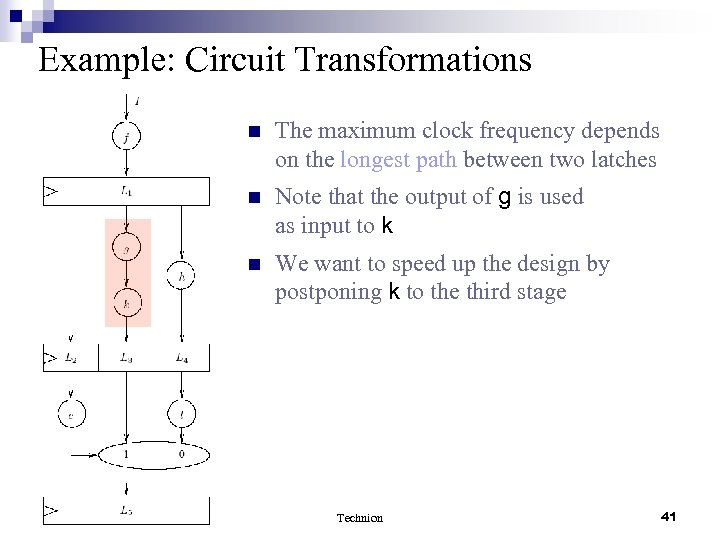Example: Circuit Transformations n The maximum clock frequency depends on the longest path between two latches n Note that the output of g is used as input to k n We want to speed up the design by postponing k to the third stage Technion 41

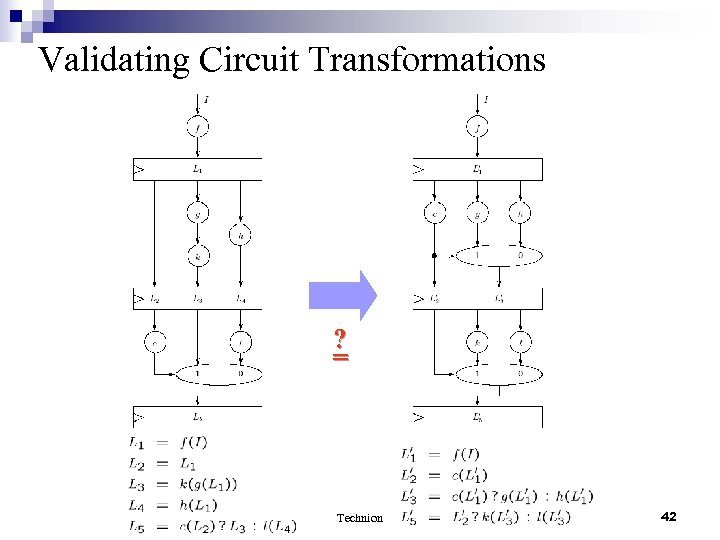Validating Circuit Transformations ? = Technion 42

Validating a compilation process n Target program n u 1 = x 1 + y 1; u 2 = x 2 + y 2; z = u 1 u 2 ; n Compilation Source program z = (x 1 + y 1) (x 2 + y 2); Need to prove that: (u 1 = x 1 + y 1 u 2 = x 2 + y 2 z = u 1 u 2) $ z = (x 1 + y 1) (x 2 + y 2) Source Target Technion 43

Validating a compilation process n Target program n u 1 = x 1 + y 1; u 2 = x 2 + y 2; z = u 1 u 2 ; n Compilation Source program z = (x 1 + y 1) (x 2 + y 2); Need to prove that: (u 1 = x 1 + y 1 u 2 = x 2 + y 2 z = u 1 u 2) $ z = (x 1 + y 1) (x 2 + y 2) f 1 f 2 g 2 Technion 44

Validating a compilation process n Instead, prove: under functional consistency: for every uninterpreted function f n x = y ! f(x) = f(y) Need to prove that: (u 1 = x 1 + y 1 u 2 = x 2 + y 2 z = u 1 u 2) $ z = (x 1 + y 1) (x 2 + y 2) n Which translates to (via Ackermann’s reduction): g f 1 f 2 g 2 Technion 45

Definitions for the proof… n A Violating cycle under an assignment R: F e. T 1 T Either dashed or solid T e. T 2 n This assignment violates T S but not necessarily T R Technion 47

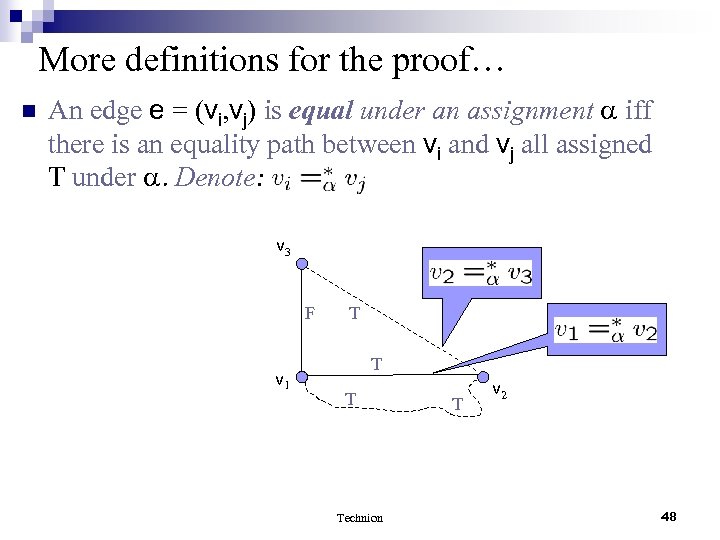More definitions for the proof… n An edge e = (vi, vj) is equal under an assignment iff there is an equality path between vi and vj all assigned T under . Denote: v 3 F v 1 T Technion T v 2 48

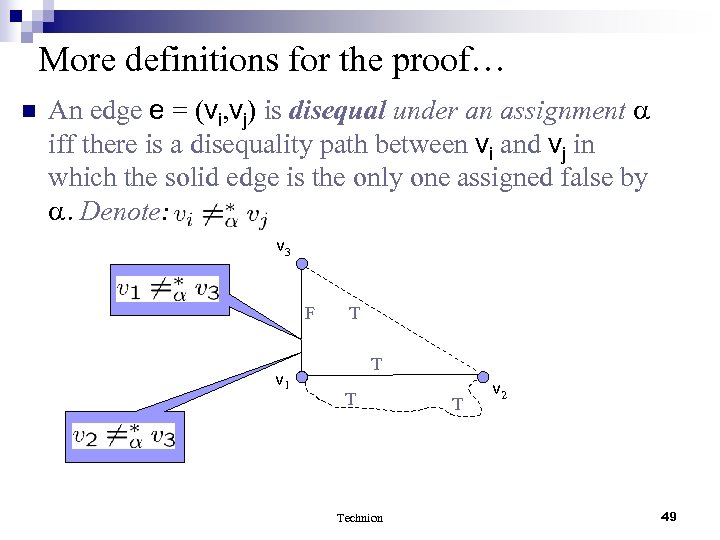More definitions for the proof… n An edge e = (vi, vj) is disequal under an assignment iff there is a disequality path between vi and vj in which the solid edge is the only one assigned false by . Denote: v 3 F v 1 T Technion T v 2 49

Proof… n Observation 1: The combination is impossible if = R (recall: R ² T R) v 3 F T v 1 n T v 2 Observation 2: if (v 1, v 3) is solid, then Technion 50

Re. Constructing S Type 1: Type 2: It is not the case that Otherwise it is not the case that v 3 F F T T v 1 n T v 1 v 2 Assign S (e 23) = F n v 2 Assign (e 13) = T In all other cases S = R Technion 51

Re. Constructing S n Starting from R, repeat until convergence: (e. T) : = F in all Type 1 cycles ¨ (e. F) : = T in all Type 2 cycles ¨ n All Type 1 and Type 2 triangles now satisfy T S n B is still satisfied (monotonicity of NNF) n Left to prove: all contradictory cycles are still satisfied Technion 52

Proof… n Invariant: contradictory cycles are not violating throughout the reconstruction. T v 3 F T T v 1 n v 2 contradicts the precondition to make this assignment… Technion 53

Proof… n Invariant: contradictory cycles are not violating throughout the reconstruction. v 3 F T T F v 1 n v 2 contradicts the precondition to make this assignment… Technion 54

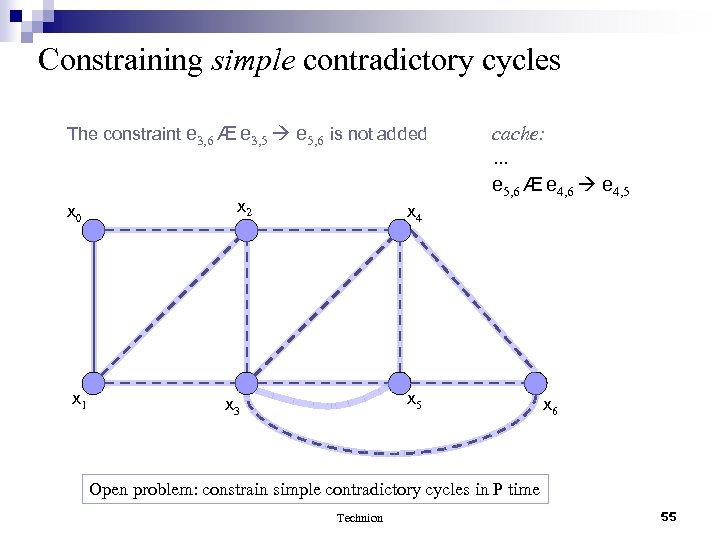Constraining simple contradictory cycles The constraint e 3, 6 Æ e 3, 5 e 5, 6 is not added x 0 x 1 x 2 cache: … e 5, 6 Æ e 4, 6 e 4, 5 x 4 x 5 x 3 x 6 Open problem: constrain simple contradictory cycles in P time Technion 55

Constraining simple contradictory cycles the constraint the graph has e 5, 6 is not added, though needed Suppose e 3, 6 Æ e 3, 5 3 more edges Here we will stop, although … cache: x 0 x 1 … e 5, 6 Æ e 4, 6 e 4, 5 x 2 x 4 x 5 x 3 x 6 Open problem: constrain simple contradictory cycles in P time Technion 56