General-Purpose Software for Large-Scale Bifurcation Analysis Andy Salinger

General-Purpose Software for Large-Scale Bifurcation Analysis Andy Salinger, Eric Phipps Computer Science Research Institute, Sandia National Laboratories Albuquerque, NM, USA Tipping Points in Complex Flows - Numerical Methods for Bifurcation Analysis of Large-Scale Systems from 31 Oct 2011 through 4 Nov 2011 Sandia is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the United States Department of Energy’s National Nuclear Security Administration under contract DE-AC 04 -94 AL 85000.

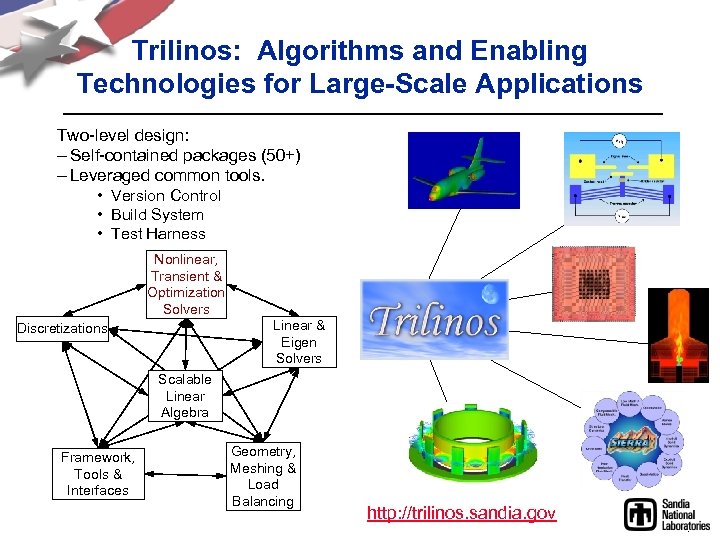
Trilinos: Algorithms and Enabling Technologies for Large-Scale Applications Two-level design: – Self-contained packages (50+) – Leveraged common tools. • Version Control • Build System • Test Harness Nonlinear, Transient & Optimization Solvers Discretizations Linear & Eigen Solvers Scalable Linear Algebra Framework, Tools & Interfaces Geometry, Meshing & Load Balancing http: //trilinos. sandia. gov

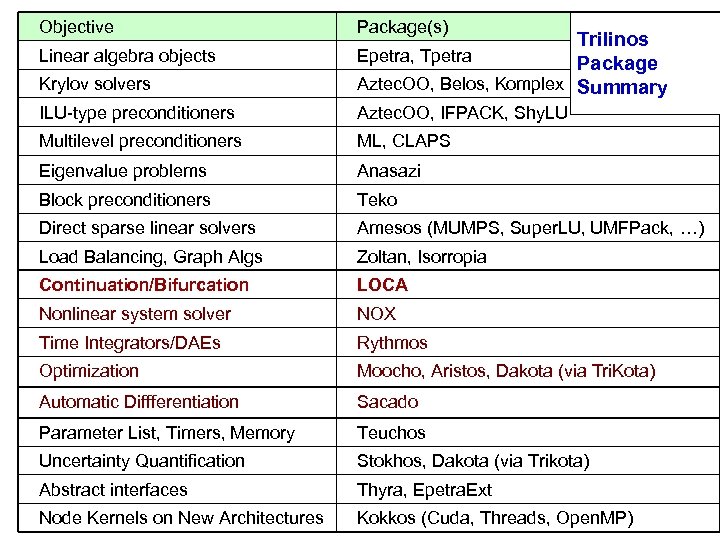
Objective Package(s) Krylov solvers Trilinos Epetra, Tpetra Package Aztec. OO, Belos, Komplex Summary ILU-type preconditioners Aztec. OO, IFPACK, Shy. LU Multilevel preconditioners ML, CLAPS Eigenvalue problems Anasazi Block preconditioners Teko Direct sparse linear solvers Amesos (MUMPS, Super. LU, UMFPack, …) Load Balancing, Graph Algs Zoltan, Isorropia Continuation/Bifurcation LOCA Nonlinear system solver NOX Time Integrators/DAEs Rythmos Optimization Moocho, Aristos, Dakota (via Tri. Kota) Automatic Diffferentiation Sacado Parameter List, Timers, Memory Teuchos Uncertainty Quantification Stokhos, Dakota (via Trikota) Abstract interfaces Thyra, Epetra. Ext Node Kernels on New Architectures Kokkos (Cuda, Threads, Open. MP) Linear algebra objects

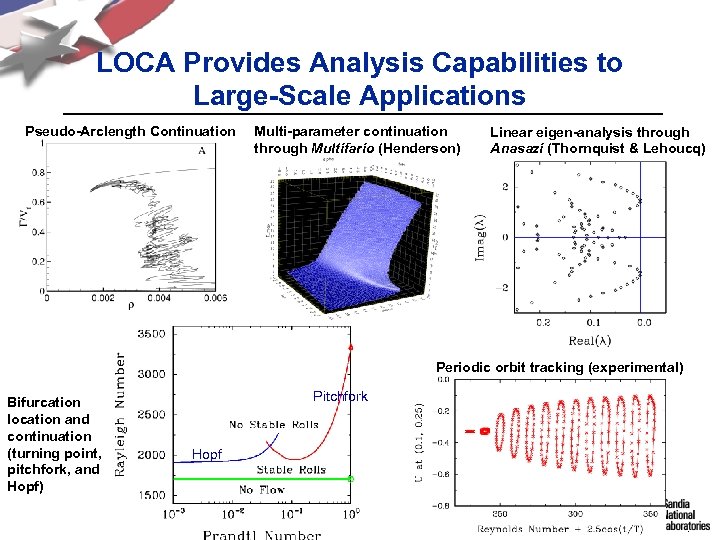
LOCA Provides Analysis Capabilities to Large-Scale Applications Pseudo-Arclength Continuation Multi-parameter continuation through Multifario (Henderson) Linear eigen-analysis through Anasazi (Thornquist & Lehoucq) Periodic orbit tracking (experimental) Bifurcation location and continuation (turning point, pitchfork, and Hopf) Pitchfork Hopf

Why Do We Need Stability Analysis Tools for Large-Scale Applications • Several powerful continuation and bifurcation analysis tools are available: – – – AUTO (Doedel et al) CONTENT (Kuznetsov et al) MATCONT (Govaerts et al) Py. DSTool (Guckenheimer et al) … • Large-scale applications have specific requirements – – Massively parallel distributed memory architectures Complicated parallel data structures and sparse matrices Application-tuned linear algebra Limited derivative capabilities • Tools and algorithms are needed that – Do not change matrix sparsity or increase memory requirements – Agnostic to linear algebra and architecture – Can be incorporated into existing simulation codes (i. e. , libraries)

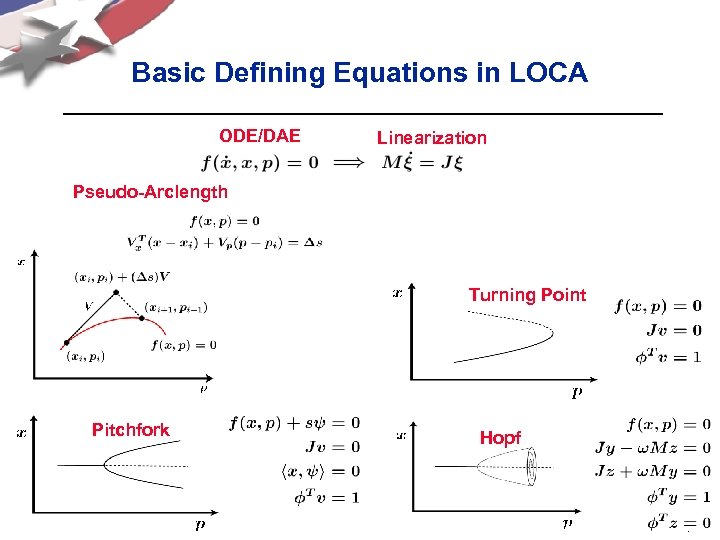
Basic Defining Equations in LOCA ODE/DAE Linearization Pseudo-Arclength Turning Point Pitchfork Hopf

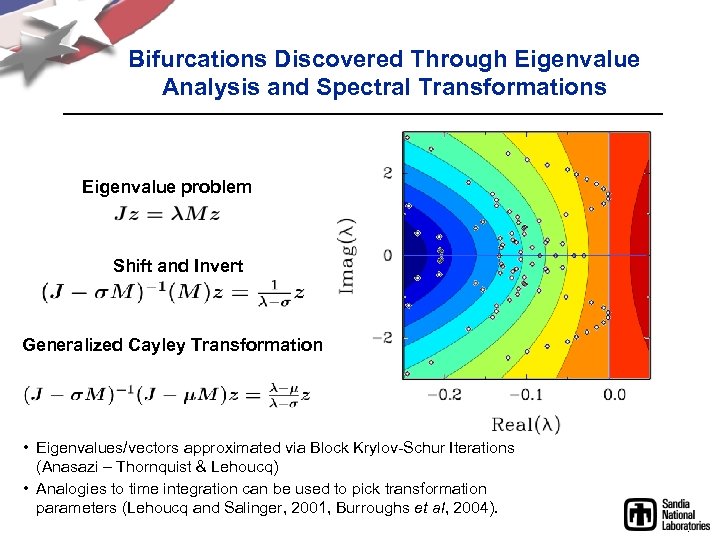
Bifurcations Discovered Through Eigenvalue Analysis and Spectral Transformations Eigenvalue problem Shift and Invert Generalized Cayley Transformation • Eigenvalues/vectors approximated via Block Krylov-Schur Iterations (Anasazi – Thornquist & Lehoucq) • Analogies to time integration can be used to pick transformation parameters (Lehoucq and Salinger, 2001, Burroughs et al, 2004).

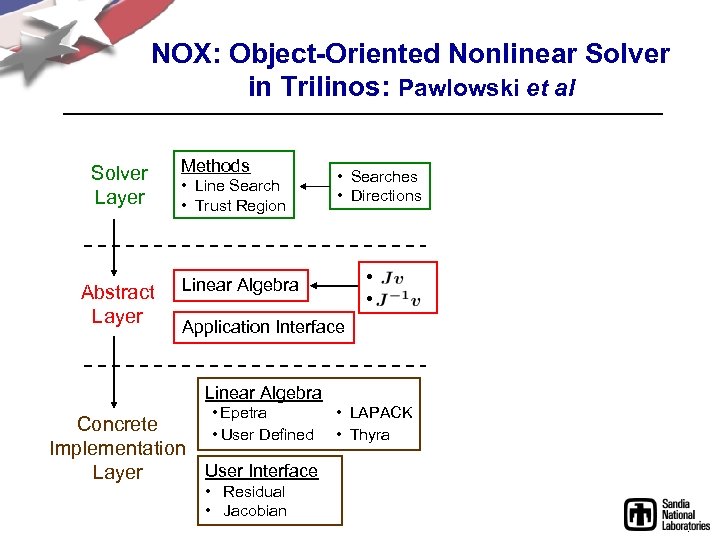
NOX: Object-Oriented Nonlinear Solver in Trilinos: Pawlowski et al Solver Layer Abstract Layer Methods • Line Search • Trust Region • Searches • Directions • • Linear Algebra Application Interface Linear Algebra • Epetra • LAPACK Thyra Concrete • User Defined • Implementation User Interface Layer • Residual • Jacobian

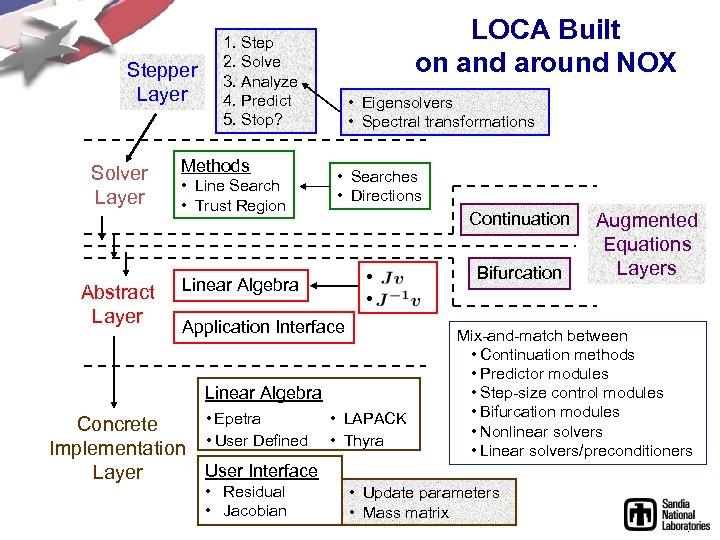
Stepper Layer Solver Layer Abstract Layer LOCA Built on and around NOX 1. Step 2. Solve 3. Analyze 4. Predict 5. Stop? Methods • Line Search • Trust Region • Eigensolvers • Spectral transformations • Searches • Directions Continuation • • Linear Algebra Application Interface Linear Algebra • Epetra • Concrete Implementation • User Defined • User Interface Layer • Residual • Jacobian LAPACK Thyra Bifurcation Augmented Equations Layers Mix-and-match between • Continuation methods • Predictor modules • Step-size control modules • Bifurcation modules • Nonlinear solvers • Linear solvers/preconditioners • Update parameters • Mass matrix

Block Elimination Algorithm for Turning Point (fold) Tracking Uses 4 Solves • Turning Point Bifurcation • Full Newton Algorithm • Block Elimination Algorithm

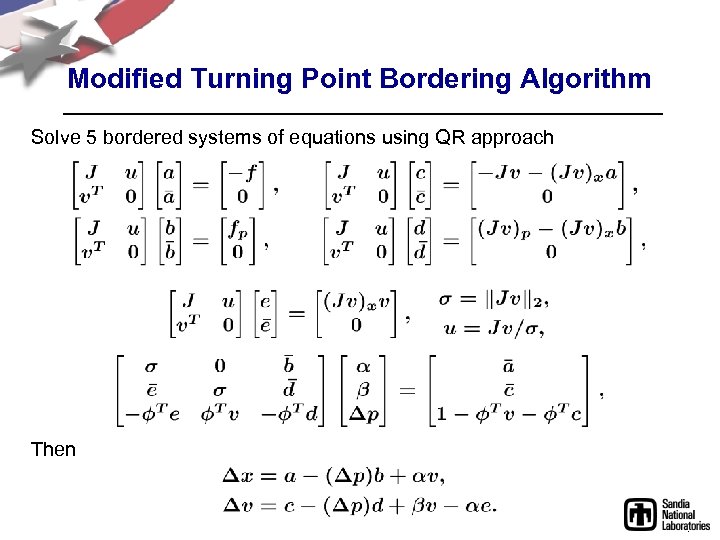
Modified Turning Point Bordering Algorithm Solve 5 bordered systems of equations using QR approach Then

Minimally Augmented Turning Point Formulation Given and , let then There are constants such that Standard formulation: Note for Newton’s method: 3 linear solves per Newton iteration (5 for modified bordering)! For symmetric problems reduces to 2 solves.

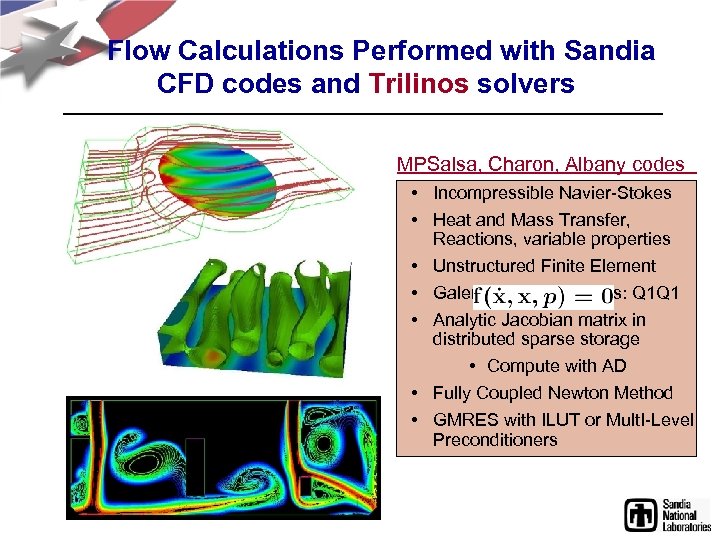
Flow Calculations Performed with Sandia CFD codes and Trilinos solvers MPSalsa, Charon, Albany codes • Incompressible Navier-Stokes • Heat and Mass Transfer, Reactions, variable properties • Unstructured Finite Element • Galerkin/Least-Squares: Q 1 Q 1 • Analytic Jacobian matrix in distributed sparse storage • Compute with AD • Fully Coupled Newton Method • GMRES with ILUT or Mult. I-Level Preconditioners

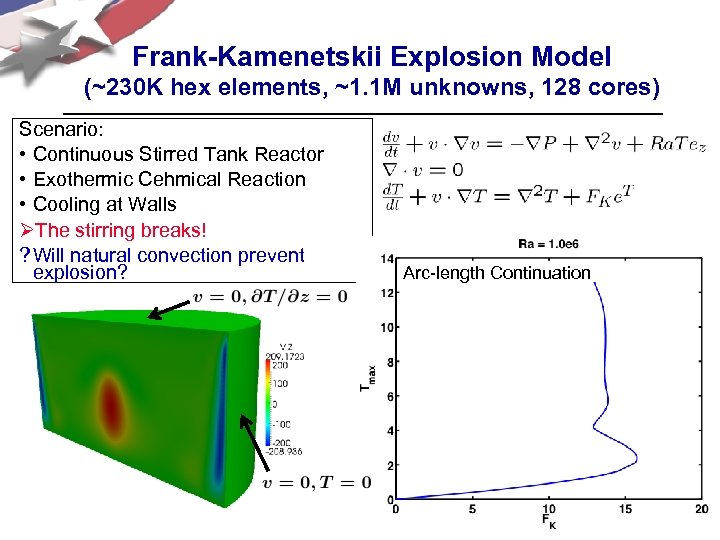
Frank-Kamenetskii Explosion Model (~230 K hex elements, ~1. 1 M unknowns, 128 cores) Scenario: • Continuous Stirred Tank Reactor • Exothermic Cehmical Reaction • Cooling at Walls ØThe stirring breaks! ? Will natural convection prevent explosion? Arc-length Continuation

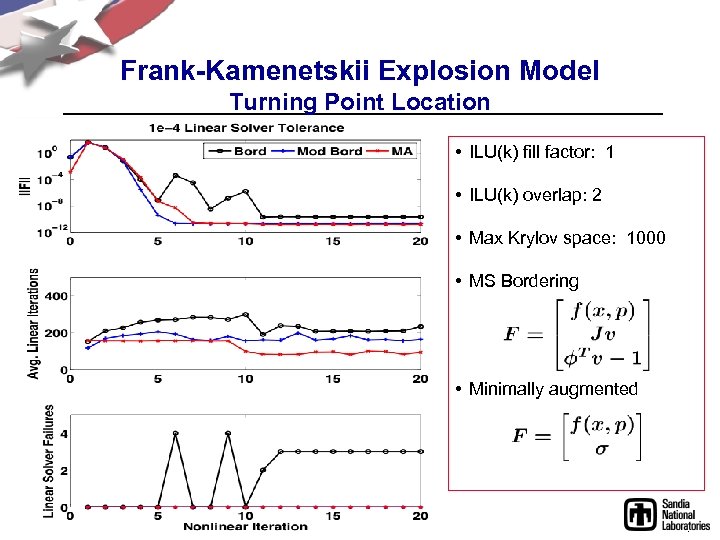
Frank-Kamenetskii Explosion Model Turning Point Location • ILU(k) fill factor: 1 • ILU(k) overlap: 2 • Max Krylov space: 1000 • MS Bordering • Minimally augmented

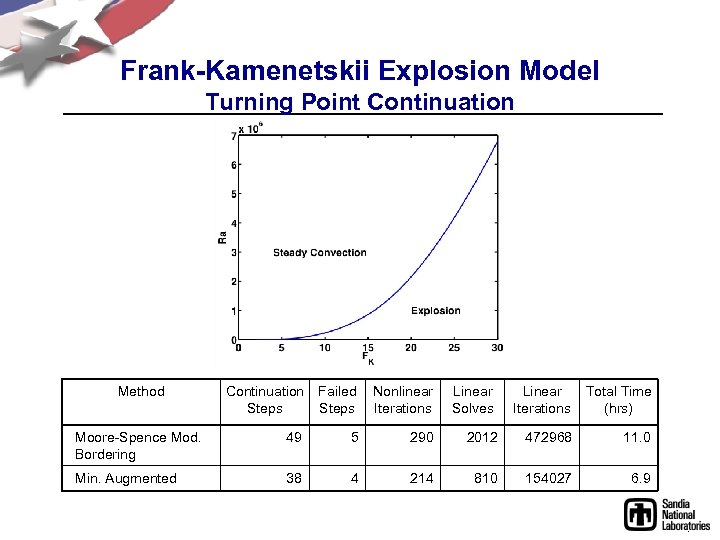
Frank-Kamenetskii Explosion Model Turning Point Continuation Method Continuation Steps Failed Steps Nonlinear Iterations Linear Solves Linear Iterations Total Time (hrs) Moore-Spence Mod. Bordering 49 5 290 2012 472968 11. 0 Min. Augmented 38 4 214 810 154027 6. 9

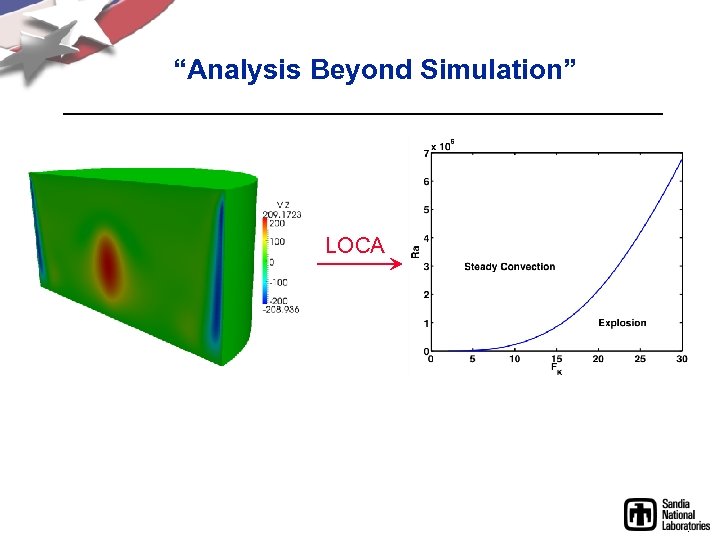
“Analysis Beyond Simulation” LOCA

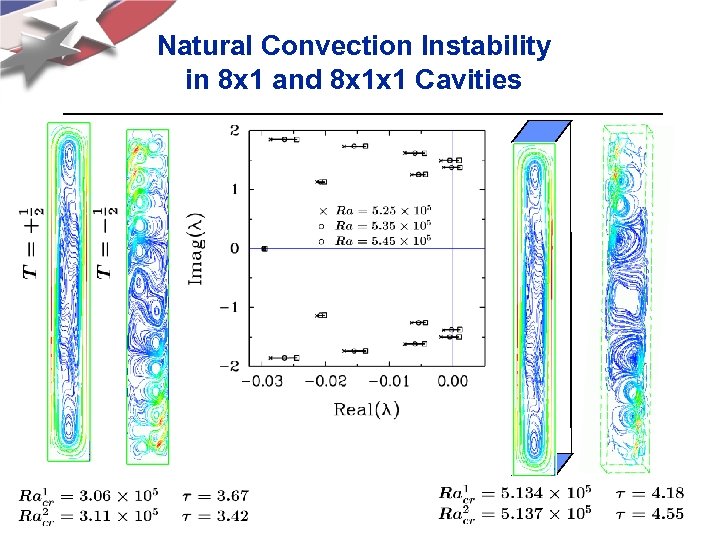
Natural Convection Instability in 8 x 1 and 8 x 1 x 1 Cavities

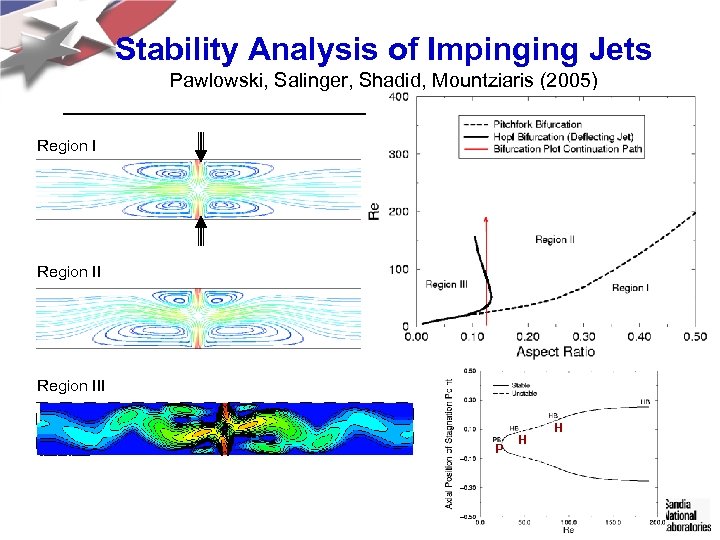
Stability Analysis of Impinging Jets Pawlowski, Salinger, Shadid, Mountziaris (2005) Region III P H H

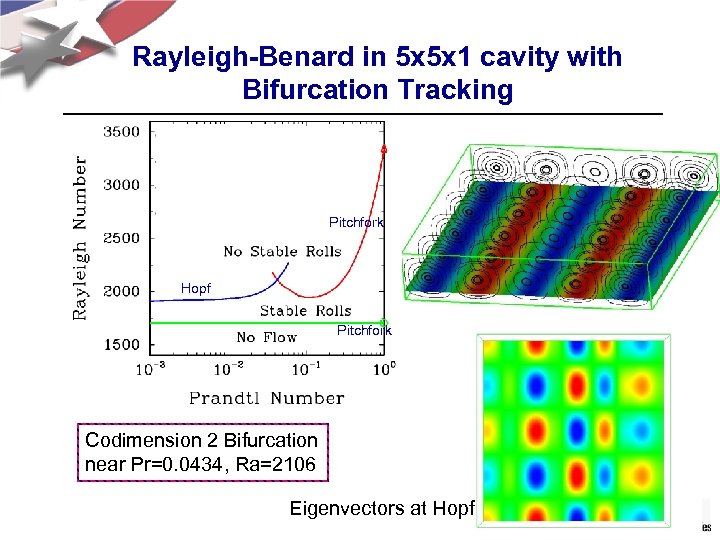
Rayleigh-Benard in 5 x 5 x 1 cavity with Bifurcation Tracking Pitchfork Hopf Pitchfork Codimension 2 Bifurcation near Pr=0. 0434, Ra=2106 Eigenvectors at Hopf

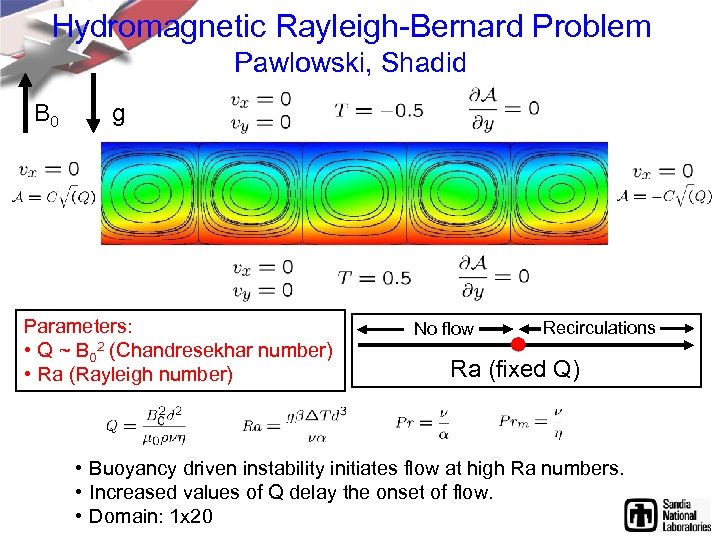
Hydromagnetic Rayleigh-Bernard Problem Pawlowski, Shadid B 0 g Parameters: • Q ~ B 02 (Chandresekhar number) • Ra (Rayleigh number) No flow Recirculations Ra (fixed Q) • Buoyancy driven instability initiates flow at high Ra numbers. • Increased values of Q delay the onset of flow. • Domain: 1 x 20

Resistive, Extended MHD Equations Extended MHD Model in Residual Form Involution:

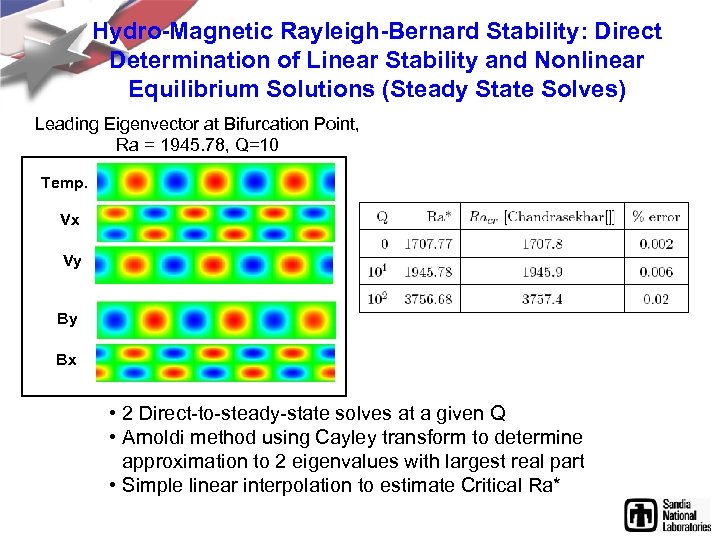
Hydro-Magnetic Rayleigh-Bernard Stability: Direct Determination of Linear Stability and Nonlinear Equilibrium Solutions (Steady State Solves) Leading Eigenvector at Bifurcation Point, Ra = 1945. 78, Q=10 Temp. Vx Vy By Bx • 2 Direct-to-steady-state solves at a given Q • Arnoldi method using Cayley transform to determine approximation to 2 eigenvalues with largest real part • Simple linear interpolation to estimate Critical Ra*

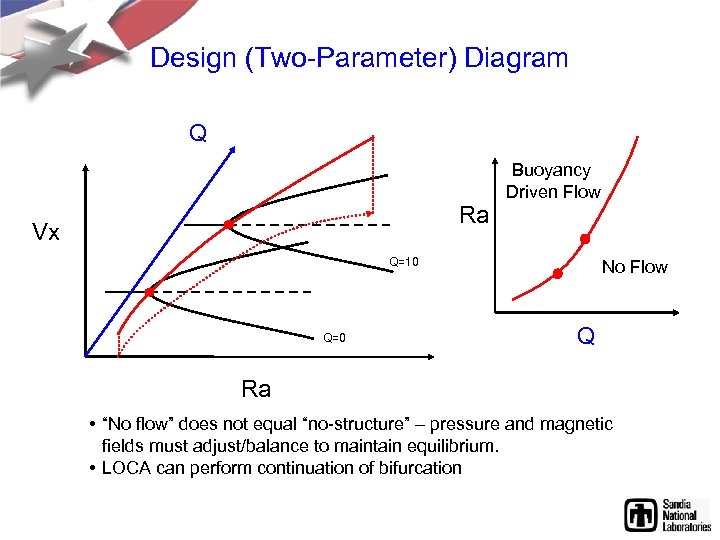
Design (Two-Parameter) Diagram Q Ra Vx Buoyancy Driven Flow Q=10 Q=0 No Flow Q Ra • “No flow” does not equal “no-structure” – pressure and magnetic fields must adjust/balance to maintain equilibrium. • LOCA can perform continuation of bifurcation

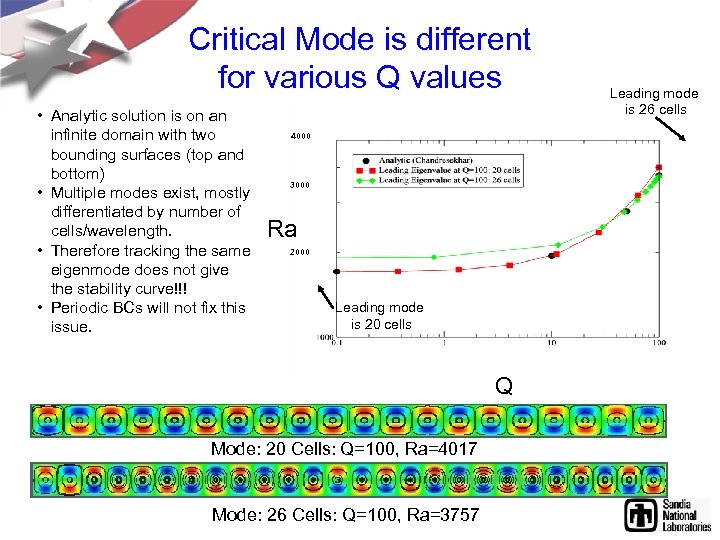
Critical Mode is different for various Q values • Analytic solution is on an infinite domain with two bounding surfaces (top and bottom) • Multiple modes exist, mostly differentiated by number of cells/wavelength. • Therefore tracking the same eigenmode does not give the stability curve!!! • Periodic BCs will not fix this issue. 4000 3000 Ra 2000 Leading mode is 20 cells Q Mode: 20 Cells: Q=100, Ra=4017 Mode: 26 Cells: Q=100, Ra=3757 Leading mode is 26 cells

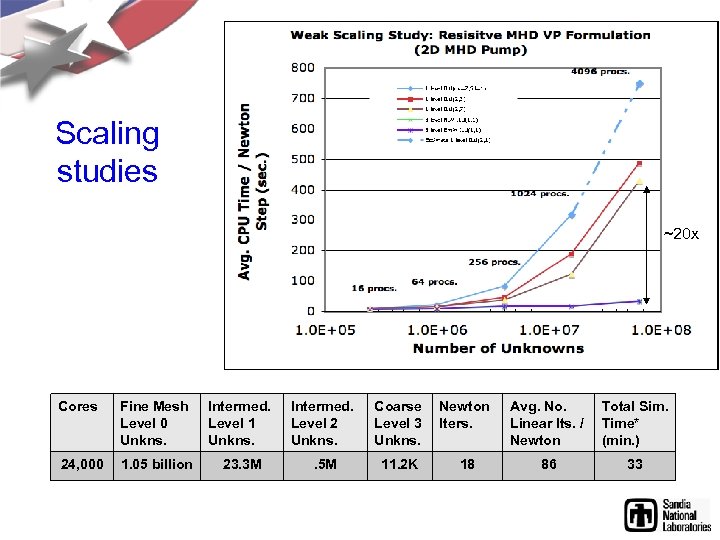
Scaling studies ~20 x Cores Fine Mesh Level 0 Unkns. Intermed. Level 1 Unkns. Intermed. Level 2 Unkns. Coarse Level 3 Unkns. Newton Iters. Avg. No. Linear Its. / Newton Total Sim. Time* (min. ) 24, 000 1. 05 billion 23. 3 M . 5 M 11. 2 K 18 86 33

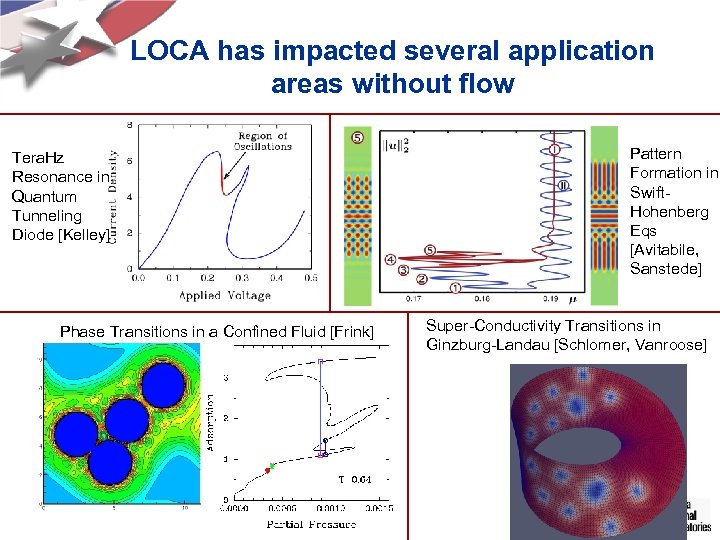
LOCA has impacted several application areas without flow Tera. Hz Resonance in Quantum Tunneling Diode [Kelley] Phase Transitions in a Confined Fluid [Frink] Pattern Formation in Swift. Hohenberg Eqs [Avitabile, Sanstede] Super-Conductivity Transitions in Ginzburg-Landau [Schlomer, Vanroose]

How do I attribute the successes that LOCA has had? 1. Algorithmic research in large-scale bifurcations 10% 2. Science demonstrations 15% 3. LOCA is hooked up to Trilinos linear solvers 75% What broader lesson is there? Build software in independent-yet-interoperable components

Build Software in Independent-yet. Interoperable Components Analysis Tools Nonlinear Solver Time Integration Continuation Sensitivity Analysis Stability Analysis Constrained Solves Optimization Linear Algebra Data Structures Iterative Solvers Direct Solvers Eigen Solver Preconditioners Matrix Partitioning Derivative Tools Derivatives Sensitivities Continuation, Bifurcation, Stability Analysis

Build Software in Independent-yet. Interoperable Components Analysis Tools Nonlinear Solver Time Integration Continuation Sensitivity Analysis Stability Analysis Constrained Solves Optimization Linear Algebra Data Structures Iterative Solvers Direct Solvers Eigen Solver Preconditioners Matrix Partitioning Derivative Tools Derivatives Sensitivities Transient sensitivity analysis

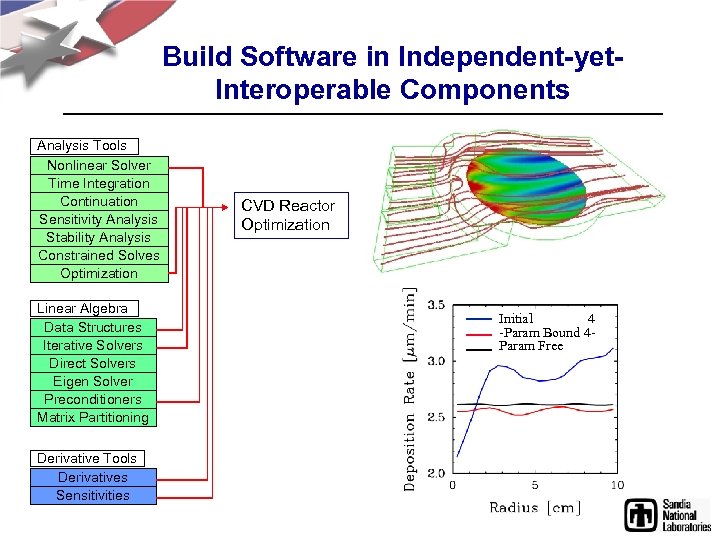
Build Software in Independent-yet. Interoperable Components Analysis Tools Nonlinear Solver Time Integration Continuation Sensitivity Analysis Stability Analysis Constrained Solves Optimization Linear Algebra Data Structures Iterative Solvers Direct Solvers Eigen Solver Preconditioners Matrix Partitioning Derivative Tools Derivatives Sensitivities CVD Reactor Optimization Initial 4 -Param Bound 4 Param Free

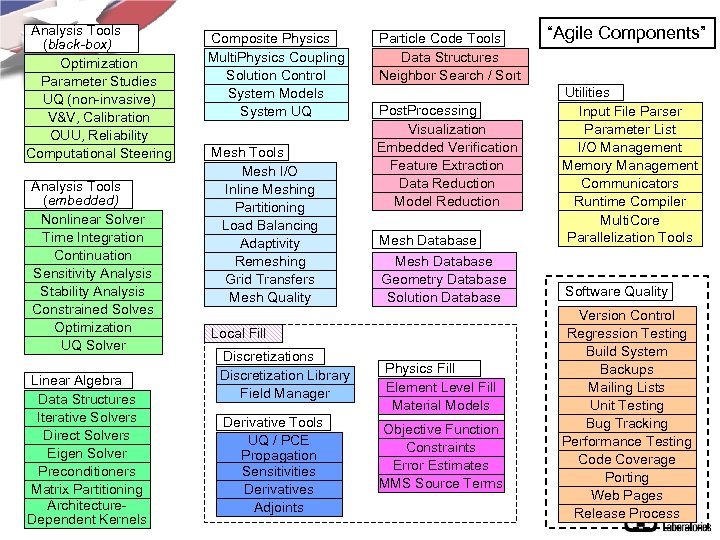
Analysis Tools (black-box) Optimization Parameter Studies UQ (non-invasive) V&V, Calibration OUU, Reliability Computational Steering Analysis Tools (embedded) Nonlinear Solver Time Integration Continuation Sensitivity Analysis Stability Analysis Constrained Solves Optimization UQ Solver Linear Algebra Data Structures Iterative Solvers Direct Solvers Eigen Solver Preconditioners Matrix Partitioning Architecture. Dependent Kernels Composite Physics Multi. Physics Coupling Solution Control System Models System UQ Mesh Tools Mesh I/O Inline Meshing Partitioning Load Balancing Adaptivity Remeshing Grid Transfers Mesh Quality Particle Code Tools Data Structures Neighbor Search / Sort Mesh Database Utilities Input File Parser Parameter List I/O Management Memory Management Communicators Runtime Compiler Multi. Core Parallelization Tools Mesh Database Geometry Database Solution Database Software Quality Post. Processing Visualization Embedded Verification Feature Extraction Data Reduction Model Reduction Local Fill Discretizations Discretization Library Field Manager Derivative Tools UQ / PCE Propagation Sensitivities Derivatives Adjoints “Agile Components” Physics Fill Element Level Fill Material Models Objective Function Constraints Error Estimates MMS Source Terms Version Control Regression Testing Build System Backups Mailing Lists Unit Testing Bug Tracking Performance Testing Code Coverage Porting Web Pages Release Process

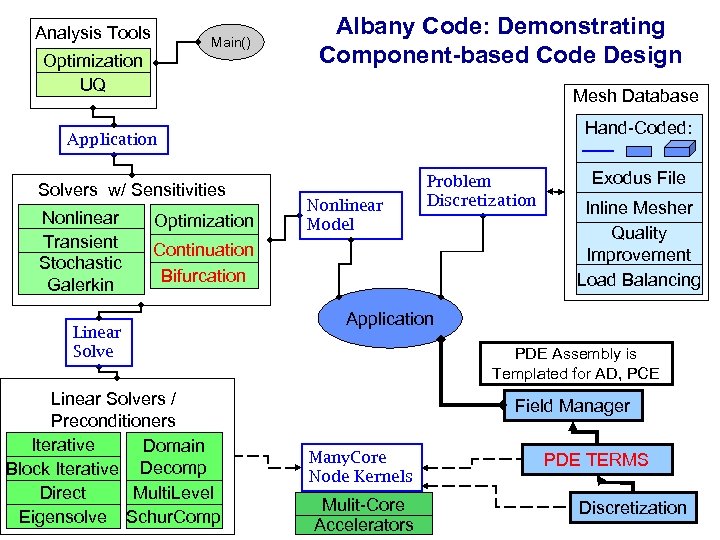
Analysis Tools Main() Optimization UQ Albany Code: Demonstrating Component-based Code Design Mesh Database Hand-Coded: Application Solvers w/ Sensitivities Nonlinear Transient Stochastic Galerkin Optimization Nonlinear Model Problem Discretization Continuation Bifurcation Linear Solvers / Preconditioners Iterative Domain Block Iterative Decomp Direct Multi. Level Eigensolve Schur. Comp Exodus File Inline Mesher Quality Improvement Load Balancing Application PDE Assembly is Templated for AD, PCE Field Manager Many. Core Node Kernels Mulit-Core Accelerators PDE TERMS Discretization

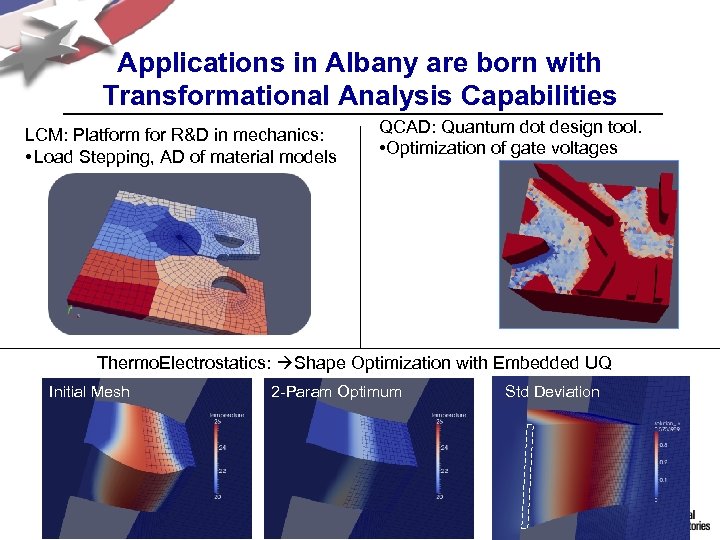
Applications in Albany are born with Transformational Analysis Capabilities LCM: Platform for R&D in mechanics: • Load Stepping, AD of material models QCAD: Quantum dot design tool. • Optimization of gate voltages Thermo. Electrostatics: Shape Optimization with Embedded UQ Initial Mesh 2 -Param Optimum Std Deviation

Summary • LOCA and Trilinos provide powerful simulation and analysis capabilities – Continuation, bifurcation, and linear stability analysis – Scalable linear algebra – Optimization, time integration, automatic differentiation, uncertainty quantification, discretization, … • Missing Capabilities (formerly future work) – More generic algorithms for bordered matrix solves • Much is hardwired to our Epetra format – Periodic Orbit tracking beyond initial attempt – Automated initial guess generation for null vectors – Better documentation, examples, error checking, etc. • Current Passion – Component-based code design with Embedded Analysis in Mind from the beginning