General Education Assessment in Mathematics Courses Finding What

General Education Assessment in Mathematics Courses: Finding What Works Teri Rysz, Ed. D Teri. Rysz @uc. edu Margaret J. Hager, Ed. D Margaret. Hager@uc. edu University of Cincinnati Clermont AMATYC Las Vegas, 11/12/2009

Beginnings l Summer, 2004 – New Associate Dean of Academics 6 General Education Math Courses were identified to be assessed. – General Education Course Assessment Plan designed by all attendees. –

Individual Assignments l Individual Assessment Assignments l Designed for all courses. l Demonstrated l Competence Rubric given to each student along with the assignment.

High Hopes l Assignment was to be given to all students in every section. l Instructors would forward responses to Coordinator. l A random sample chosen to be ‘graded’ with rubric previously given to student.

Would a Random Sample Work? l My argument was to have the assignments given every quarter to every student, thereby making the process something that instructors would have as a regular part of their syllabus.

Feedback l Based on feedback from the first two rounds (with limited instructor buy-in): Three assignments were tweaked. – It could work, but needed more consistency with all instructors. –

Changing of the Guard l Current Associate Dean decided that random sections would be assessed. l Coordinator was inconsistent in getting this information to instructors in a timely manner (once given to me in last week of the quarter ).

What Happened Next? l Frustrated with the process, and deep into writing a dissertation, I could no longer be involved. l Coordinator was getting paid to do it, but wasn’t following through. l Needed ‘New Blood’: – Dr. Teri Rysz

General Education Mathematics Courses at Clermont l Math for Behavioral Sciences I (MATH 136) l Math for Behavioral Sciences II (MATH 137) l Statistics for Health Sciences (MATH 146) l College Algebra I (MATH 173) l Finite Math & Calculus I (MATH 225) l Calculus & Analytic Geometry I (MATH 261)

Pilot Study College Algebra I (MATH 173) Search for simple assessment question – 2 major concepts a successful College Algebra I student learns – 10 real world application questions for inverse functions – Colleague asked to choose question to ask students – Question to current College Algebra I instructors

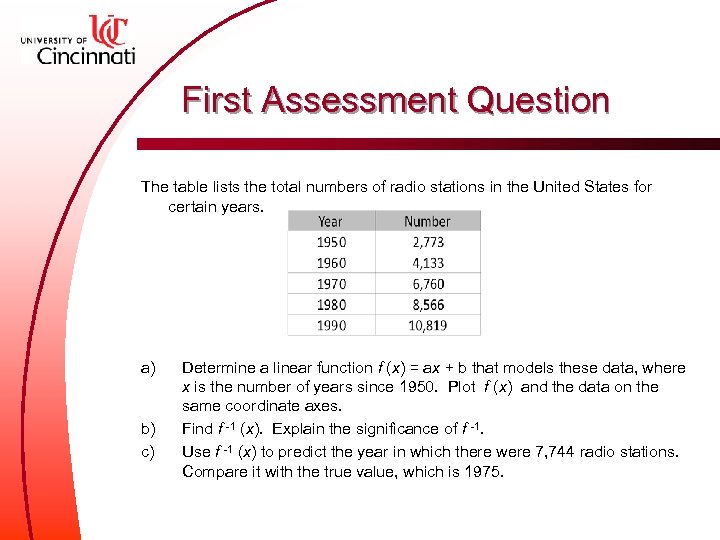First Assessment Question The table lists the total numbers of radio stations in the United States for certain years. a) b) c) Determine a linear function f (x) = ax + b that models these data, where x is the number of years since 1950. Plot f (x) and the data on the same coordinate axes. Find f -1 (x). Explain the significance of f -1. Use f -1 (x) to predict the year in which there were 7, 744 radio stations. Compare it with the true value, which is 1975.

Rubric l 1 point – f (x) = 201. 15 x + 2, 773 Slope could be anything close to 201. 15. l 1 point – f -1 (x) = (x – 2, 773)/201. 15 If incorrect function in part a, 1 point for correct inverse function from stated function l 1 point – inverse function predicts the year for a given number of radio stations l 1 point – correct year for the inverse function determined or explanation of the process for a correct prediction l 0 points - no correct responses

Results Score Count 0 19 1 11 2 3 3 2 4 7 l 42 scores l Mean of 1. 2 l 21. 4% scored 3 or better

Revisions l Graphing extraneous, eliminate plot directions l Because the data was not exactly linear, some students decided a function could not be determined. “Use the number of radio stations in the first and last year to determine an average rate of change for the slope in the function. ” l Question was asked with different risk factors – Two sections: question on final exam – One section: review for final exam

Expectations for Next Round l Mean of 1. 5 (1. 2) l 30% (21. 4%) score a 3 or better l Subsequent reflection on further editions to the question and/or instruction.

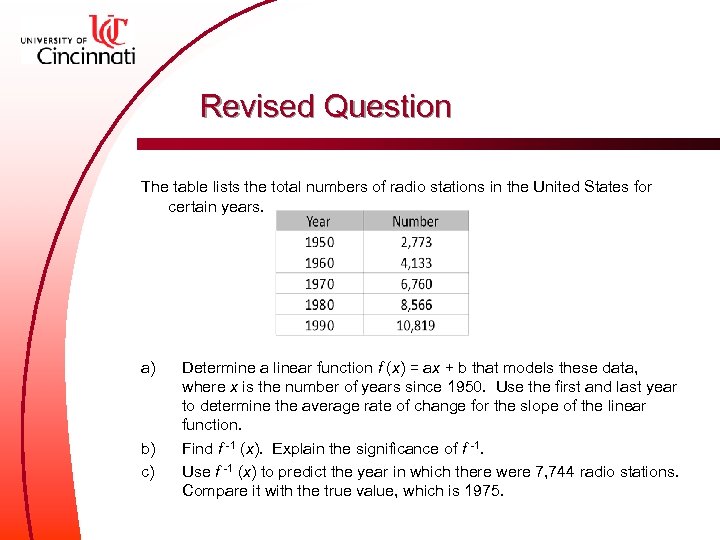Revised Question The table lists the total numbers of radio stations in the United States for certain years. a) b) c) Determine a linear function f (x) = ax + b that models these data, where x is the number of years since 1950. Use the first and last year to determine the average rate of change for the slope of the linear function. Find f -1 (x). Explain the significance of f -1. Use f -1 (x) to predict the year in which there were 7, 744 radio stations. Compare it with the true value, which is 1975.

Revised Results Score 0 Count 9 l 1 2 3 4 19 scores l one section “disappeared” l Mean of 1. 52 (1. 5) l 31. 6% (30%) scored 3 or better 2 2 1 5

Plans Mathematics for Behavioral Sciences II A student observes the spinner below and claims that the color red has the highest probability of appearing since there are two red areas on the spinner. What is your reply? – Rubric l 1 point – compares yellow area to red area l 1 point – yellow has 50% of the area l 1 point – yellow is greater area l 1 point – yellow has higher probability l 0 point – only false statement or no statement is made – Results – Score 0 1 2 3 4 Count 4 8 10 11 12 45 responses Mean is 2. 4 51. 1% scored 3 or better

Plans (continued) Academic Assessment Committee l Mathematics instructors meeting – Full time and adjunct – Improves instruction → improves learning – Collaborate and cooperate to learn from results l Continue building assessment coverage and on-time reports l