eda21c559e42fd7372bb5f43bb07b5ab.ppt
- Количество слайдов: 70

General Concepts Players: Alice, Bob and Trudy. How to communicate securely over an insecure medium? Alice should be able to send a message to Bob That Trudy can't understand or modify and Bob is assured that Alice is the sender.

Types of Attaches Passive Attacks: The attacker eavesdrops and read/record messages in transit. Active Attacks: The attacker may: Transmit new messages, l Replay old essages, l Modify/Delete messages on transit. l

Fundamental Tenet of Cryptography l If lots of smart people failed to solve a problem, then it probably won't be solved (soon). l The time required to break a code should be longer than the time the encrypted data must remain secret. l The value of most data decreases overtime.

Cryptographic System: Algorithm + Key l It is perfectly OK to let everyone know the algorithm. Knowledge of the algorithm without the key does not help unmangle the information. l Publishing the algorithm provides an enormous amount of free consulting to uncover weaknesses.

Layers and Cryptography l l l Application (e. g. , PEM), Transport (e. g. , SSL), Network (e. g. , IPsec).

Trojan horse/virus/worm: Malicious code written by bad guys. Modern mail systems & Internet connectivity (Cable Modems/DSL) contribute to its spread. Virus Checkers: looks for instruction sequences for known viruses and uses message digests for files.

Covert Channels : Very low bandwidth (e. g. , 1 bit every 10 seconds), but can be used to steal cryptographic keys. Steganography: Hide secret messages in other messages.

Traditional use of cryptography: plaintext >>>> ciphertext >>>>>>> plaintext (encryption) (decryption) cryptographer: invent clever secret codes. cryptanalyst: attempt to break these codes.

¢ ¢ Fundamental Tenet of Cryptography: If lots of smart people failed to solve a problem, then it probably won't be solved (soon). The time required to break a code should be longer than the time the encrypted data must remain secret. The value of most data decreases overtime. ¢

¢ Cryptographic System: Algorithm + Key ¢ It is perfectly OK to let everyone know the algorithm because knowledge of the algorithm without the key does not help unmangle the information. Publishing the algorithm provides an enormous amount of free consulting to uncover weaknesses.

¢ Computational Difficulty: Example: combination lock ¢ Typically require 3 numbers between 1 and 40. If it takes 10 seconds for a good guy, it would take 10*(40**3) seconds or about 1 week for the bad guy. By requiring 4 numbers, If it takes 13 seconds for the good guy, it would take 13*(40**4) seconds or about 1 year for the bad guy!In general, increasing the key length by 1 bit makes the good guy's job just a little bit harder, but makes the bad guy's job twice as hard!

¢ ¢ Example of Secret Codes: Caesar cipher: substitute each letter with another letter which is 3 letters away in the alphabet (with wrap around). E. g. , dozen >>> grcho. Extension: Instead of 3 use any number n between 1 and 25. E. g. , for n=1, HAL >>> IBM. ¢ Monoalphabetic cipher: arbitrary map one letter to another. There are 26!=4*(10**26) possibilities. If each possibility takes 1 microsecond it would take 10 trillion years to try all possibilities. However statistical analysis of language makes it much easier to break.
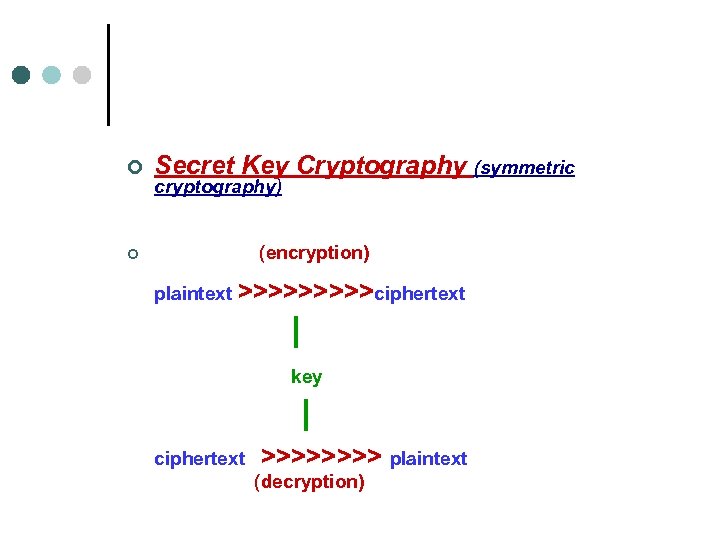
¢ Secret Key Cryptography (symmetric ¢ (encryption) cryptography) plaintext >>>>>ciphertext | key | ciphertext >>>> plaintext (decryption)

¢ Can be used for: • Transmission Over an Insecure Channel: see unintelligible data. • Secure Storage on Insecure Media: irrevocably lost. • ¢ ¢ ¢ An eavesdropper will only Forgetting the key makes the data Authentication: Alice authenticating Bob: Alice Bob challenge: r >>>>>>> r response: K{r} <<<<<<< K{r} - r is a random number, - K{r} is the secret key encryption of r using shared key K.

¢ Public Key Cryptography (asymmetric cryptography) ¢ Each individual has two keys: ¢ private key (not revealed to anyone) public key (make it known to everyone) (encryption) plaintext >>>>> ciphertext | public key ¢ private key | ciphertext >>>>> plaintext (decryption)

¢ The reverse process is called digital signature: ¢ (signing) plaintext >>>>> ciphertext | private key public key | ciphertext >>>> plaintext (verification) ¢ Public key cryptographic algorithms are orders of magnitude slower than the best known secret key cryptographic algorithms. Thus they normally used to established temporary shared secret key for use during a session.

¢ Uses of Public Key Cryptography: ¢ Transmission Over an Insecure Channel: <> Alice Bob {K}e. B >>>>> [K]d. B K{m. B} >>>>> K{m. B} K{m. A} <<<<< K{m. A}

¢ Secure Storage on Insecure Media: ¢ Alice generates a random key K and save: 1. F= K{File} KF= {K} e. A ¢ To restore the file: 1. K= [KF] d. A File = K{F}

¢ Authentication: Alice authenticating Bob: ¢ Alice ¢ Bob challenge: c = { r }e. B >>>>> c response: r <<<<< r = [c]d. B

¢ Hash Algorithms (also known as message ¢ ¢ digest/fingerprint, one-way functions) The hash of a message m, h=H(m) has the following properties: Given m, it is easy to compute h. Given h, it is hard to compute m. Given m, it is hard to find another m' such that H(m) = H(m'). It is hard to find m 1 and m 2 such that H(m 1) = H(m 2).

¢ Uses of Hash Algorithms: MAC/MIC (Message Authentication/Integrity Code) • ¢ Using Secret Key: ¢ Alice sends Bob receives m, h where h = H(m|K) >> m, h , OK if h = H (m|K) ¢ ¢ -K is the shared secret between Alice and Bob is sure that Alice sent the message, since she knows K. Bob can NOT prove to any one that Alice sent him message m, since he also knows K.

• ¢ Password Hashing: OS like UNIX stores the hash of passwords instead of storing the actual passwords. For each user U, there is a tuple <U, h> where h = H(P) is the hash of password P of user U. When a user U types a password, P, the OS compute H(P) and if it is equal to the saved value h in the tuple <U, h> the user is OK.

¢ The magic of XOR: A Simple XOR symmetric algorithm: (from Bruce Shneier textbook) ¢ 0 ® 1 = 1 1 ® 0 = 1 0 ® 0 = 0 1 ® 1 = 0 ¢ Note that: ¢ a ® a = 0 a ® b = a (since b ® b = 0) ¢ The following program is a very simple symmetric algorithm. (see /home/cs 772/public_html/demos/xor ) To decrypt, the ciphertext C is XORed with a key K to produce a plaintext P. P ® K = C To encrypt, the plaintext P is XORed with a key K to produce a ciphertext C. C ® K = P (since (P ® K) ® K = P)

¢ Secret Key Cryptography ¢ General Block Encryption: ¢ Secret key cryptographic systems take a reasonable length key (e. g. , 64 bits) and generate a one-one mapping that looks, to someone who does not know the key, completely random. I. e. , any single bit change in the input result in a totally independent random number output.

¢ Types of transformation for k-bit blocks: ¢ Substitution: For small values of k, specify for each of the 2 k possible values of the input, the k-bit output. ¢ which it goes. Permutation: Specify for each of the I input bits, the output position to


Hashes and Message Digests ¢ ¢ A hash or message digest, is a one-way function since it is not practical to reverse. A function is cryptographicaly secure if it is computationally infeasible to find: • • • a message that has a given message digest. a different message with the same message digest. two messages that have the same message digest. ¢ Major Algorithms: ¢ Ron Rivest Message Digest MD-family ¢ NIST Secure Hash Algorithm SHA-1: 160 -bit. They take an arbitrary-length string and map it to a fixed-length quantity that appears to be randomly chosen. For example, two inputs that differ by only one bit should have outputs that look like completely independently chosen random numbers. Ideally, the message digest function ¢ 128 -bit. (MD 2, MD 4 and MD 5): should be easy to compute. Like secret key algorithms. digest algorithms tends to be computed in rounds. The designers finds the smallest number of rounds necessary before the output passes various randomness tests and then add few more to be safe.

¢ Things to do with a Hash ¢ Authentication: Alice authenticating Bob: Alice Bob challenge: r >>>>>>> r response: d <<<<<<< d=MD{K|r} ¢ ¢ - r is a random number, - MD{K|r} is the message digest of K concatenated with r. Alice computes MD{K|r} and if equal d, then Bob must know K. ¢ Computing a MAC: Using Secret Key K between Alice and Bob ¢ ¢ Alice sends Bob receives m, d where d = MD(K|m) >> m, d , OK if d = MD (K|m)

¢ Encryption: ¢ Generating one-time pad: Both Alice and Bob knows the shared secret K and generates: ¢ b 1= MD(K) bi = MD(K|bi-1), i=2, 3, . . Alice sends Bob receives ci = mi ® bi >> ci and computes mi= ci ® bi

¢ Public Key Cryptography ¢ All secret key algorithms & hash algorithms do the same thing but public key algorithms look very different from each other. ¢ The thing that is common among all of them is that each participant has two keys, public and private, and most of them are based on modular arithmetic.

¢ Modular Arithmetic ¢ x mod n is the remainder of x when divided by n. e. g. , 8 mod 10 = 8, 18 mod 10 = 8, 24 mod 10 = 4

¢ Multiplication: Example: multiplication mod 10 8 x 8 = 4, 1 x 9 = 9 , 7 x 6 = 2 ¢ ¢

¢ ¢ ¢ Multiplication by 1, 3, 7 and 9 works as a cipher since it performs 1 -1 mapping. Example: if k = 7, then 1987 is encrypted to 7369 decryption is done by multiplying each digit by k-1 , the multiplicative inverse of k. A multiplicative inverse of k is the number to multiply by k to get 1. Example: if k = 7, then k-1 is 3 since 7 x 3 = 1 In the above table (Fig. 6 -2), each "1" is the intersection of k and k-1. Only the numbers {1, 3, 7, 9} have multiplicative inverse mod 10.

¢ ¢ ¢ What is so special about the set {1, 3, 7, 9}? These numbers are relatively prime to 10, i. e. , they do not share with 10 any common factors other than 1. Note that 9 is not a prime number but it is relatively prime to 10. How many numbers less than n are relatively prime to n? This quantity is referred to as Ø(n) and is called the totient function. o ¢ then {1, 2, . . . , n-1} are all relatively prime and thus Ø(n) = n-1. o ¢ ¢ If n is prime: If n = p. q where p and q are two distinct primes, then Ø(n) = (p-1)(q-1). Example: for n = 10 = 2. 5, Ø(10) =(2 -1). (5 -1)=1. 4=4, which is the set {1, 3, 7, 9}.

¢ ¢ Exponentation: Example: exponentiation mod 10 4 2 = 6, 8 8 = 6, 19 = 9 , 76 = 9 An exponentiative inverse of e is the number d such that: e. d = 1 mod Ø(n) ¢ Example: For n= 10, Ø(10)=4: ¢ e=3 and d=7 are exponentiative inverses since 3. 7=21= 1 mod 4

¢ ¢ ¢ ¢ ¢ Encrypt/Decrypt: To encrypt m: compute c = me mod n To decrypt c: compute m = cd mod n Example: encrypt m = 8: c = 83 = 2 decrypt c=2: m = 27 = 8 Sign/Verify: To sign m: compute s = md mod n To verify s: compute m = se mod n Example: sign m = 8: s = 87 = 2 verify s=2: m = 23 = 8 In public cryptography: <e, n> is public key & <d, n> is private key

¢ RSA Algorithm: ¢ ¢ generate public & private keys pair: 1. choose two large primes p and q. (typically 256 bits each & keep them secret). 2. compute n = p. q & Ø(n) = (p-1)(q-1). (it is very hard to factor n into p & q). 3. choose a number e that is relatively prime to Ø(n). 4. find a number d that is the multiplicative inverse of e mod Ø(n), i. e. , e. d = 1 mod Ø(n). 5. your public key: <e, n> & private key: <d, n>.

¢ ¢ ¢ encrypt/decrypt: To encrypt a message m (<n): c = me mod n & To decrypt c: m = cd mod n This works since: cd mod n = (me)d mod n = me. d mod n = m mod n // since e. d = 1 mod Ø(n) = m // since m < n ¢ ¢ ¢ sign/verify: To sign a message m (<n): s = md mod n & To verify s: m = se mod n This also works since: se mod n = me. d mod n = m

¢ ¢ Why is RSA Secure: Every one knows the public key: <e, n>. To find the private key <d, n> you need to know Ø(n) since e. d = 1 mod Ø(n). To know Ø(n) you need to p and q since Ø(n) = (p 1). (q-1). Thus to break RSA you should know how to factor n to find p and q. Factoring a big number like n is hard. (the best technique to factor 512 bit number will take 30, 000 MIPS-years!)

¢ ¢ ¢ ¢ Efficiency of RSA Operations: Exponentiation How to compute 12354 mod 678? 1232 = 123 = 15129 = 213 mod 678 1233 = 123. 213 = 26199 = 435 mod 678 1234 = 123. 435 = 53505 = 621 mod 678 . . . 12354 = . . . = 87 mod 678 This requires 54 small number multiplications and 54 small number divisions. How to compute 123 32 mod 678? 1232 = 123 = 15129 = 213 mod 678 1234 = 213 = 45369 = 621 mod 678 1238 = 621 = 385641 = 537 mod 678 12316 = 537 = 288369 = 219 mod 678 12332 = 219 = 47961 = 501 mod 678 This requires 5 multiplications and 5 divisions instead of 32. To efficiently compute 123 54 : 54 is represented in binary as: 1 0 | | | (((( (1232)123 ) 2 )2123 )2 This requires 8 multiplications and 8 divisions instead of 32. Each 1 requires two multipliactions and two divisions and each 0 requires one multipliaction and one division. Thus in the above we have three 1 s and two 0 s that yeilds 3. 2+2. 1=8 (we ignore the leading 1). Another example: y 14 , 14 is represented in binary as: 1 1 0 | | (( ( y 2) y ) 2 y ) 2 This requires 5 multiplication's and 5 divisions instead of 32.

The RSA keys: ¢ public key: <3|65537, n> private key: <d , n>. ¢ ¢

¢ Diffie-Hellman ¢ Alice and Bob agree on: p (large ¢ ¢ ¢ prime) & g < p. Alice Bob Pick SA (512 -bit random number) Pick SB (512 -bit random number) Compute TA = ( g. SA) mod p Compute TB = (g. SB) mod p TA >>> <<< TB Compute X = TB SA mod p Compute Y = TA SB mod p X is the same as Y! why? X = TBSA = g B A Y = TASB = g A B (SASB ) by knowing g (SA ) & g (SB ) No one can compute g S S ¢ S S

¢ Email Security Protocols: PEM & S/MIME ¢ PEM (Privacy Enhanced Mail): Add encryption, authentication and integrity to ordinary text messages. ¢ MIME (Multipurpose Internet Mail Extensions): Is a standard for encoding arbitrary data in email (images, video, etc. ). ¢ S/MIME: Incorporated many principles of PEM into MIME. ¢

¢ 1. MIC-CLEAR From: Alice To: Bob Subject: Colloquium Date: Tue Oct 26, 2005 -----BEGIN PRIVACY ENHANCED MESSAGE----- Proc-Type: 4, MIC-CLEAR Content-Type: RFC 822 Originator-ID-Asymmetric: <certificate ID> MIC-Info: RSA-MD 5, RSA, <encoded MIC> ¢ Dear Bob: I would like to invite you to give a colloquium next Fall, if you accept, let us talk about the details. Alice -----END PRIVACY ENHANCED MESSAGE----¢

¢ 3. ENCRYPTED From: Alice To: Bob Subject: Colloquium Date: Tue Oct 26, 2005 -----BEGIN PRIVACY ENHANCED MESSAGE----- Proc-Type: 4, ENCRYPTED DEK-Info: DES-CBC, IV Content-Type: RFC 822 Originator-ID-Asymmetric: <Originator certificate ID> Key-Info: RSA, <encoded message key encrypted with originator public key> MIC-Info: RSA-MD 5, RSA, <encoded encrypted MIC> ¢ ¢ Recipient-ID-Asymmetric: <Recipient certificate ID> Key-Info: RSA, <encoded message key encrypted with recipient public key> <encoded encrypted message using DES-CBC> -----END PRIVACY ENHANCED MESSAGE-----

¢ SSL/TLS Protocols ¢ SSL (Secure Socket Layer, developed by Netscape ) & TLS (Transport Layer Security, is an IETF standard) are almost the ¢ ¢ ¢ same. They run as a user-level processes on top of TCP/IP. The Basic Protocol: {==================== Alice Bob I want to talk, ciphers I support, Ra > < certificate, cipher I choose, Rb choose secret S, compute K= f (S, Ra, Rb): {S}Bob , {keyed hash of handshake msgs} > compute K= f(S, Ra, Rb): < {keyed hash of handshake msgs} ¢ < data protected with keys derived from K > ¢ ====================} ¢

¢ ¢ ¢ ¢ ¢ Keys: Alice chooses a random number S, known as the pre-master secret. It is shuffled with Ra and Rb to produce a master secret K. Ra and Rb are 32 octets long, the first 4 are the UNIX time (seconds since Jan 1, 1970). This ensures that Rs are always different. The master secret is shuffled with the two Rs to produce six (6) keys: Three for each side for encryption, integrity, and IV. The three keys used for transmission are known as the write keys while three used for receipt are known as the read keys Thus Alice's write keys are Bob's read keys and vice versa. To ensure that the keyed hash Alice sends is different from the keyed hash Bob sends, Alice include the string "CLNT" and the Bob include "SRVR" in the hash. Note that Alice has authenticated Bob, but Bob has no idea to whom he's talking In SSL it is optional for the server to authenticate the client, if he has a certificate. Normally the server authenticates the user using: <name, password> sent securely over the ssl connection.

¢ Authentication Systems ¢ ¢ Password-based Authentication ¢ It's not who you know. It's what you know ¢ ¢ On-line Password attack: Easy to defend, limit and slow down the number of guesses. ¢ Off-line Password attack: Capture a quantity X derived from the password and take your time to guess (e. g. , use a dictionary) the passwd that produces X.

¢ Address-based Authentication ¢ It's not what you know. It's where you are ¢ In Unix implementations: ¢ /etc/hosts. equiv: Contains a list of computers that have identical user accounts. allow users on these hosts to login (rsh) without providing passwords.

¢ Trusted Intermediaries If we have N nodes: ¢ If each nodes keeps N-1 secrets, ¢ then adding a new node involves adding N new secrets, one at each node. Clearly not practical for large N. KDC (Key Distribution Center): KDC knows N keys, one for each node. Adding a new node involves only adding one key at KDC. If Alice like to talk to Bob: Alice KDC Bob Need to talk to Bob ---> random R R= KA[X] <--- X= KA{R} Y= KB{R} ---> R= KB[Y] ¢ ¢ ¢ C 1 = R{M 1} -----------> M 1 = R[C 1] M 2 = R[C 2] <----------- C 2 = R{M 2} Disadvantages of KDC: If compromised, all Keys are compromised. Single point of failure Performance bottleneck.

¢ ¢ ¢ ¢ CA (Certificate Authority): Each node keeps its private key. The CA certifies (sign) that the public key belong to the node and everyone trust the CA that he checked this fact for each node. All public key certificates may be kept in one place or each node keeps its own certificate and presents it to whoever asks for it. Certifies expire after a reasonable period (e. g. , 1 year) but can be revoked at any time and the CA periodically publish a CRL (certificate revocation list) that contains all the revoked certificates. Clients should check the latest CRL before trusting a certificate.

¢ Session Key Establishment ¢ It is a good idea to generate a separate key for each session to use for encryption/decryiption of session data following the session authentication phase. Why? • • Keys a kind of "wear out" if used a lot! The availability of more cipher text, the more likely an intruder may find the key. Prevent replay and decryption of previously recorded message.

¢ Delegation It's not who you are. It's who you're working for Sometime it is necessary to have some entity act on your behave. One possible means of allowing this is to give your password to this entity. This is not usually a good idea (please never do that! oducsc). ¢ ¢ The best mechanism to achieve that is delegation (or authentication forwarding). Generate a special message, signed by you (using public key cryptography, or through the use of KDC), specifying: To whom you are delegating the rights, Which rights are being delegated & For how long.

¢ Passwords Problems: • • • ¢ Eavesdropping. Read stored file. Easy to guess on-line. Easy to crack off-line. Users may write it down. On-Line Password Guessing

¢ Helpful Tips: • • • Set limit on the number of trials. Process incorrect passwords s l o w l y Report to users of unsuccessful attempts. Assign users an easy to pronounce strings as passwords. Do not let users choose easy-toguess passwords. Force users to change passwords

¢ ¢ Off-Line Password Guessing Obtaining a hash of a password h, an attacker can guess the password w and checks to see if h = MD (w). ¢ ¢ ¢ ¢ If some one obtains a file F containing the hashes of many passwords, e. g. , /etc/passwd he can perform a dictionary attack : for each word w in dictionary D do compute h = MD (w) for each e in F do if e = h then w as a password done The number of performed hashes is: |D|

¢ Storing a random number s (salt) with e = MD (w|s) makes it harder for a dictionary attack: ¢ for each entry <s, e> in F do for each word w in the dictionary D do ¢ compute h = MD (w|s) if e = h then w as a password done ¢ done The number of performed hashes is: |D|. |F|

¢ ¢ ¢ How long should a password be? To protect against on-line attack: short password is fine. E. g. , ATM systems have 4 digits (10, 000 different PIDs), it is ¢ ¢ ¢ OK since you only have 3 guesses before rejecting your card. To protect against off-line attack: 64 bits of randomness makes the number of trials 264 which is considered computationally hard: In decimal this is about 20 digits to remember. If we select random characters (from a 64 chars of upper case, lower case, digits, punctuations) we need 11 characters. If generate pronounceable passwords (case-insensitive and every third char is one of the 6 vowels) we need 16 characters. If we allow humans generated passwords, we need 32 characters.

General Tips: ¢ Do not exchange passwords using email. ¢ Use different passwords on different systems or accounts. ¢ Change your password frequently. ¢ Abort Login Trojan Horses (e. g. , type Alt-Ctrl-Del). ¢

¢ Mutual Authentication ¢ ¢ Shared Secret ¢ Protocol 7: {================ Alice Bob I'm Alice > f(K, Rb) > Ra > < f(K, Ra) < Rb ================}

¢ ¢ Protocol 8: Reduce number of messages in Protocol by putting more than one item of information into each message: {================ Alice Bob I'm Alice, Ra > f(K, Rb) > < Rb, f(K, Ra) ================}

¢ Pitfall 1: Reflection Attack ¢ Trudy can impersonate Alice to Bob by oppening a second connection to Bob (or to another sever that share the same secret with Alice): ¢ Session 1: {================= Trudy ob B ¢ I'm Alice, Ra > < b, f(K, Ra) R suspend session 1. . . ¢ Session 2: {================= Trudy Bob I'm Alice, Rb > < Rb', f(K, Rb) abort session 2. . . . =================} ¢ continue session 1. . . f(K, Rb) > =================} ¢

¢ Pitfall 2: Passwod guessing Trudy mount an off-line password guessing attack: {==================== ¢ Trudy Bob I'm Alice, Ra > < Rb, f(K, Ra). . suspend session and use: Ra, and f(K, Ra) to guess K. ====================}
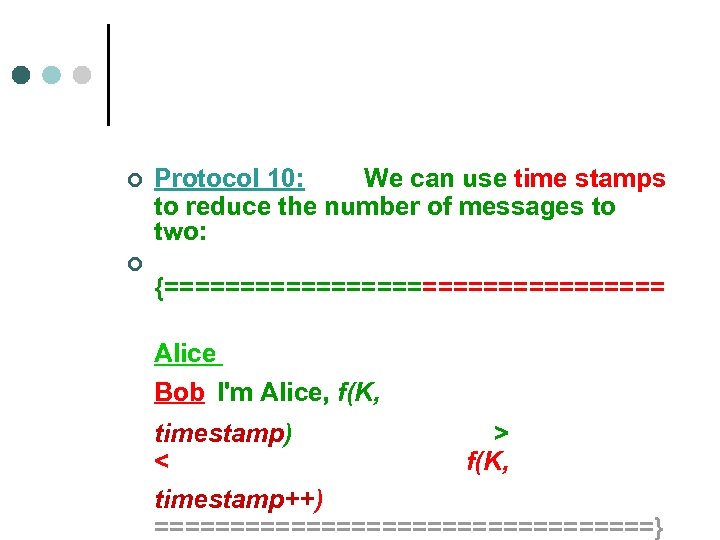
¢ ¢ Protocol 10: We can use time stamps to reduce the number of messages to two: {================= Alice Bob I'm Alice, f(K, timestamp) > < f(K, timestamp++) =================}

Mediated Authentication ¢ ¢ The Basic Needham-Shroeder Protocol {=================== Alice KDC Bob N 1, Alice wants Bob > < Ka {N 1, "Bob", Kab, ticket to Bob}, where ticket to Bob = Kb {Kab, "Alice"} ¢ ¢ ¢ ¢ ticket to Bob, Kab{N 2} > < Kab{N 2 --, N 3} Kab {N 3 --} > ===================} N is a "nonce", a number that is used only once (e. g. , a sequence numer, random number, timestamp). N 1: to prevent Trudy from impersonating KDC and replaying old replies to Alice. N 2 and N 3 are challenges for mutual authentication.

¢ ¢ The Kerberos Authentication Protocol: It is based on Needham-Shroered protocol, but is much simpler since it is based on timestamp and the ticket includes expiration date. ¢ {=================== Alice KDC Bob ¢ N 1, Alice wants Bob > < Ka{N 1, "Bob", Kab, ticket to Bob}, where ticket to Bob = Kb {Kab, "Alice", expiration time} ¢ ¢ ticket to Bob, Kab{timestamp} > < Kab{timestamp++} ===================}
eda21c559e42fd7372bb5f43bb07b5ab.ppt