Gene-Environment Case-Control Studies Raymond J Carroll Department of

Gene-Environment Case-Control Studies Raymond J. Carroll Department of Statistics Center for Statistical Bioinformatics Institute for Applied Mathematics and Computational Science Texas A&M University http: //stat. tamu. edu/~carroll

Note the Maroon color scheme! And the green MSU flag.

Apologies to Dr. Seuss

Michigan State Grads at TAMU Mohsen Pourahmadi Soumen Lahiri

Other Michigan State Contacts David Ruppert Anton Schick

Outline • Problem Case-Control Studies with Gene: Environment relationships • Theme I Logistic regression is lousy for : understanding interactions. We make assumptions that can double or triple the effective sample size

Outline • Problem Case-Control Studies with Gene: Environment relationships • Theme II There is a lousy estimator, and a : good one that makes more assumptions. How do you protect yourself if the assumptions fail, and you want to analyze 500, 00 SNP?

Outline • Problem Case-Control Studies with Gene: Environment relationships • Theme III How does all this work with actual : data, as opposed to simulated data?

Software • SAS and Matlab Programs Available at my web site under the software button http: //stat. tamu. edu/~carroll • R programs available from the NCI • New Statistical Science paper 2009, volume 24, 489 -502

Basic Problem Formalized • Gene and Environment • Question For women who carry the BRCA 1/2 : mutation does oral contraceptive use , provide any protection against ovarian cancer?

Basic Problem Formalized • Gene and Environment • Question For people carrying a particular : haplotype in the VDR pathway , does higher levels of serum Vitamin D protect against prostate cancer?

Basic Problem Formalized • Gene and Environment • Question If you are a current smokerare you : , protected against colorectal adenoma if you carry a particular haplotype in the NAT 2 smoking metabolism region?

Retrospective Studies • D = disease status (binary) • X = environmental variables • Smoking status • Vitamin D • Oral contraceptive use • G = gene status • Mutation or not • Multiple or single SNP • Haplotypes

Prospective and Retrospective Studies • Retrospective Studies : Usually called casecontrol studies • Find a population of cases i. e. , people with a , disease, and sample from it. • Find a population of controls i. e. , people , without the disease, and sample from it.

Prospective and Retrospective Studies • Retrospective Studies : Because the gene G and the environment X are sample after disease status is ascertained

Basic Problem Formalized • Case control sample: D = disease • Gene expression: G • Environment, can include strata: X • We are interested in main effects for G and X along with their interaction as they affect development of disease

Logistic Regression • Logistic Function : • The approximation works for rare diseases

Prospective Models • Simplest logistic model withoutan interaction • The effect of having a mutation (G=1) versus not (G=0) is

Prospective Models • Simplest logistic model withan interaction • The effect of having a mutation (G=1) versus not (G=0) is

Empirical Observations • Statistical Theory. There is a lovely statistical : theory available • It says: ignore the fact that you have a casecontrol sample, and pretend you have a prospective study

When G is observed • Logistic regression is robust to any modeling assumptions about the covariates in the population • Unfortunately it is not very efficient for understanding interactions • Much larger sample sizes are required for interactions that for just gene effects

Gene-Environment Independence • In many situations, it may be reasonable to assume G and X are independently distributed in the underlying population , possibly after conditioning on strata • This assumption is often used in geneenvironment interaction studies

G-E Independence • Does not always hold! • Example polymorphisms in the smoking : metabolism pathway may affect the degree of addiction

Gene-Environment Independence • If you are willing to make assumptions about the distributions of the covariates in the population, more efficiency be obtained. can • This is NOT TRUEfor prospective studies, only true for retrospective studies.

Gene-Environment Independence • The reason is that you are putting a constraint on the retrospective likelihood

Gene-Environment Independence • Our Methodology. Is far more general than : assuming that genetic status and environment are independent • We have developed capacity for modeling the distribution of genetic status given strata and environmental factors • I will skip this and just pretend G-E independence here

More Efficiency, G Observed • Our model: G-E independence and a genetic model, e. g. , Hardy-Weinberg Equilibrium

The Formulation • Any logistic model works • Question What methods do we have to : construct estimators?

Methodology • I won’t give you the full methodology, but it works as follows. • Case-control studies are very close to a prospective (random sampling) study, with the exception that sometimes you do not observe people

Methodology N Total Population Cases in the Population Np 1 Cases in the Sample n 1 n 0 Np 1 -n 1 Np 0 -n 0 Missing Cases % of Cases observed Np 0 Controls in the Population Controls in the Sample Missing Controls % of Controls observed

Pretend Missing Data Formulation • This means that there is a missing data problem. • The selection into the case control study is biased: cases are vastly over-represented • Ordinary logistic regression computes the probability of disease given the environment, given the gene, and given that the person was selected into the case control study

Pretend Missing Data Formulation • This means that there is a missing data problem. • Our method computes the probability of disease and the probability of gene given the environment and given that the person was selected into the case control study • The selection into the case control study is biased: cases are vastly over-represented

Methodology • Our method has an explicit form, i. e. , no integrals or anything nasty • It is easy to program the method to estimate the logistic model • It is likelihood based. Technically, a semiparametric profile likelihood

Methodology • We can handle missing gene data • We can handle error in genotyping • We can handle measurement errors in environmental variables, e. g. , diet

Methodology • Our method results in much more efficient statistical inference

More Data • What does More efficient statistical inference mean? • It means, effectively, that you have more data • In cases that G is a simple mutation, our method is typically equivalent to having 3 times more data

How much more data: Typical Simulation Example • The increase in effective sample size when using our methodology

Real Data Complexities • The Israeli Ovarian Cancer Study • G = BRCA 1/2 mutation (very deadly) • X includes • age, • ethnic status (below), • parity, • oral contraceptive use • Family history • Smoking • Etc.

Real Data Complexities • In the Israeli Study, G is missing in 50% of the controls, and 10% of the cases • Also, among Jewish citizens, Israel has two dominant ethnic types • Ashkenazi (European) • Shephardic (North African)

Real Data Complexities • The gene mutation BRCA 1/2 if frequent among the Ashkenazi, but rare among the Shephardic • Thus, if one component of X is ethnic status, then pr(G=1 | X) depends on X • Gene-Environment independence fails here • What can be done? Model pr(G=1 | X) as binary with different probabilities!

Israeli Ovarian Cancer Study • Question Can carriers of the BRCA 1/2 mutation : be protected via OC-use?

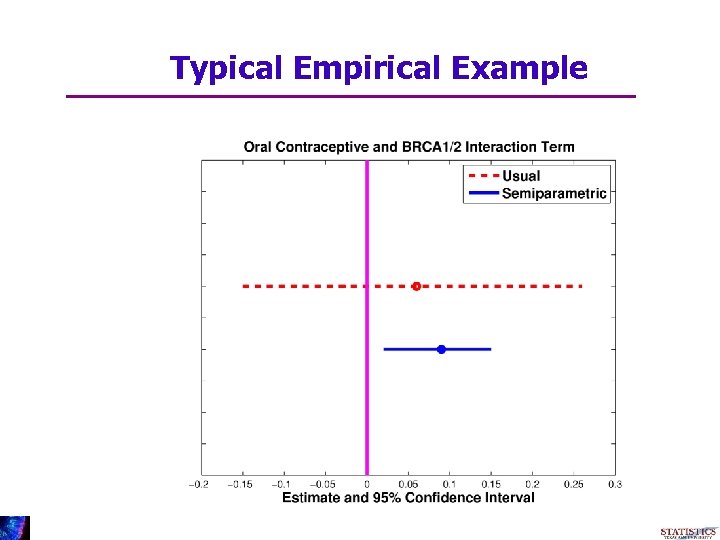Typical Empirical Example

Israeli Ovarian Cancer Study • Main Effect of BRCA 1/2 :

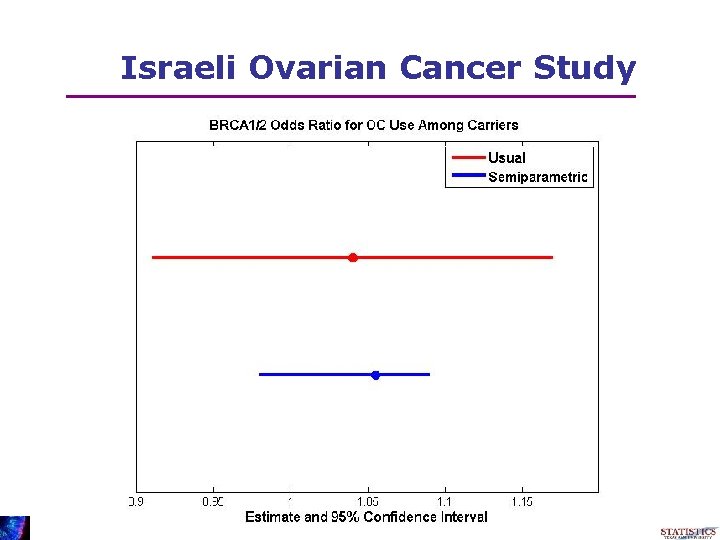Israeli Ovarian Cancer Study

Haplotypes • Haplotypes consist of what we get from our mother and father at more than one site • Mother gives us the haplotype hm = (Am, Bm) • Father gives us the haplotype hf = (af, bf) • Our diplotype is Hdip = {(Am, Bm), (af, bf)}

Haplotypes • Unfortunately, we cannot presently observe the two haplotypes • We can only observe genotypes • Thus, if we were really Hdip = {(Am, Bm), (af, bf)}, then the data we would see would simply be the unordered set (A, a, B, b)

Missing Haplotypes • Thus, if we were really Hdip = {(Am, Bm), (af, bf)}, then the data we would see would simply be the unordered set (A, a, B, b) • However, this is also consistent with a different diplotype, namely Hdip = {(am, Bm), (Af, bf)} • Note that the number of copies of the (a, b) haplotype differs in these two cases • The true diploid = haplotype pair is missing

Missing Haplotypes • Our methods handle unphased diplotyes (missing haplotypes) with no problem. • Standard EM-algorithm calculations can be used • We assume that the haplotypes are in HWE, and have extended to cases of non-HWE

Robustness • Robustness We are making assumptions to gain : efficiency = “get more data” • What happens if the assumptions are wrong? • Biases, incorrect conclusions, etc. • How can we gain efficiency when it is warranted, and yet have valid inferences?

Two Likelihoods • The two likelihoods lead to two estimators • The former is robustbut not efficient • The latter is efficientbut not robust • What to do?

Empirical Bayes • The idea is to take a weighted average of the model free and model based estimators • The weight depends on how different the estimators are • Relative to how variable the difference is

Empirical Bayes • You can actually formally test the hypothesis of whether the model fits the data • It is just a t-test on the difference between the two estimators

Empirical Bayes • If the difference is small relative to the variability, then this argues in favor of the model based approach

Empirical Bayes • We chose an Empirical Bayes type-approach • Let • Then and

Comments on Empirical Bayes • If the model fails, then the estimator converges to the model-free estimator • If the model holds, the estimator estimates the right thing, but is much more efficient than the model-free estimator

Example 1: Prostate Cancer • G = SNPs in the Vitamin D Pathway • X = Serum-level biomarker of vitamin D (diet and sun) • The VDR gene is downstream in the pathway, hence unlikely to influence the level of X • Gene-environment independence likely

Example 1: Prostate Cancer • 3 age groups • 9 centers • Two haplotype-serum Vitamin D interactions • Three haplotype main effects

Example 2: Colorectal Adenoma • G = SNPs in the NAT 2 gene, which is important in the metabolism of • X =Various measures of smoking history • The NAT 2 gene may make smokers more addicted • Gene-environment independence unlikely

Example 2: Colorectal Adenoma • Two genders • 4 age groups • 7 common haplotypes as main effects • One haplotype known to affect metabolism • Current and former smoking interactions

The NAT 2 Example • Current smoking and 101010 haplotype interaction coefficient Method Estimate s. e. p-value Model Free -0. 63 0. 17 0. 014 Independence -0. 33 0. 16 0. 048 Consistent EB 1 -0. 59 0. 25 0. 017 • Current smokers with this haplotype are 50% less likely develop a colorectal adenoma to

The VDR Example • Serum Vitamin D and 000 haplotype interaction coefficient Method Estimate s. e. p-value Model Free -0. 21 0. 12 0. 093 Independence -0. 18 0. 019 Consistent EB 1 -0. 19 0. 08 0. 021 • Men with 1 sd greater Serum vitamin D then the norm are 70% less likely develop to prostate cancer

Genome-Wide Association Studies • These methods are routinely applied to GWAS • My last two examples were actually from the PLCO GWAS • Also, can call the environment = other SNP

Summary • Case-control studies are the backbone of epidemiology in general, and genetic epidemiology in particular • Their retrospective nature distinguishes them from random samples = prospective studies

Summary • We start by assuming relationships between the genes and the “environment in the population, ” e. g. , independence • This model can be fully flexible • We also, where necessary, specify distributions for genes

Summary • We calculated a new likelihood function, leading to more much more precise inferences • The method can handle missing genes , genotyping errors , measurement errors in the environment • Calculations are straightforward via the EM algorithm

Summary • Forced to face the dilemma • Lousy but robust method • Great but not robust method • We developed a fast, data adaptive, novel way of addressing this issue • In cases where one can predict the outcome, the EB method works as desired

Acknowledgments • This work is joint with Nilanjan Chatterjee (NCI) and Yi-Hau Chen (Academia Sinica)

Acknowledgments • This work is supposed by – NCI-R 27 -CA 057030 – NHLBI RO 1 -HL 091172 (P. I. , N. Chatterjee) – Texas A&M Institute of Applied Mathematics and Computational Science through KAUST (King Abdullah University of Science and Technology)