6d56e62486184d10b32bee9b3cc3253c.ppt
- Количество слайдов: 43
 GCSE - Higher P 2 Calculator Assessment 1
GCSE - Higher P 2 Calculator Assessment 1
 Question 1 (i) Find the value of: (give your answer to 1 dp) Using a Calculator 7. 8 12. 5 – 6. 8 (ii) Find the value of: (give your answer to 3 sf) √ 2. 7³ – 15. 3
Question 1 (i) Find the value of: (give your answer to 1 dp) Using a Calculator 7. 8 12. 5 – 6. 8 (ii) Find the value of: (give your answer to 3 sf) √ 2. 7³ – 15. 3
 Question 2 Standard Form Use you calculator to work out the value of the following, giving your answers in standard form. (i) 2. 71 × 106 – 4. 8 × 105 (ii) 3. 4 × 106 ÷ 1. 7 × 10 -2
Question 2 Standard Form Use you calculator to work out the value of the following, giving your answers in standard form. (i) 2. 71 × 106 – 4. 8 × 105 (ii) 3. 4 × 106 ÷ 1. 7 × 10 -2
 Question 3 Trial & Improvement Solve by Trial & Improvement to 1 dp: x³ + 4 x = 48
Question 3 Trial & Improvement Solve by Trial & Improvement to 1 dp: x³ + 4 x = 48
 Question 4 % Change A house’s value decreases from £ 165, 000 to £ 130, 000. Find the % decrease in its value to the nearest %.
Question 4 % Change A house’s value decreases from £ 165, 000 to £ 130, 000. Find the % decrease in its value to the nearest %.
 Question 5 % – Compound Interest A person invests £ 5, 000 for 3 years at a rate of 3. 75% per annum. Calculate the value of their investment after the 3 years.
Question 5 % – Compound Interest A person invests £ 5, 000 for 3 years at a rate of 3. 75% per annum. Calculate the value of their investment after the 3 years.
 Question 6 % – Finding the Original A leather settee is reduced in a sale by 30%. It now costs £ 595. Calculate the price of the settee before the reduction.
Question 6 % – Finding the Original A leather settee is reduced in a sale by 30%. It now costs £ 595. Calculate the price of the settee before the reduction.
 Question 7 Nth Term & Sequences (i) Find the Nth term in the following sequence: 1, 4, 7, 10, 13 (ii) What would the 20 th term be?
Question 7 Nth Term & Sequences (i) Find the Nth term in the following sequence: 1, 4, 7, 10, 13 (ii) What would the 20 th term be?
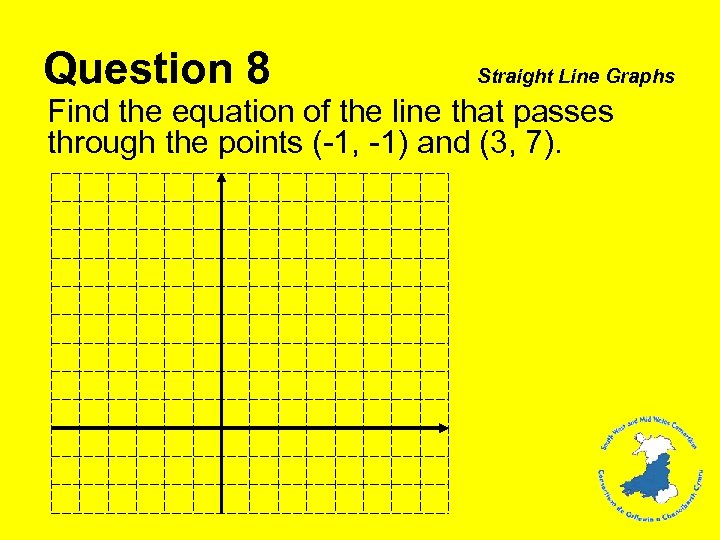 Question 8 Straight Line Graphs Find the equation of the line that passes through the points (-1, -1) and (3, 7).
Question 8 Straight Line Graphs Find the equation of the line that passes through the points (-1, -1) and (3, 7).
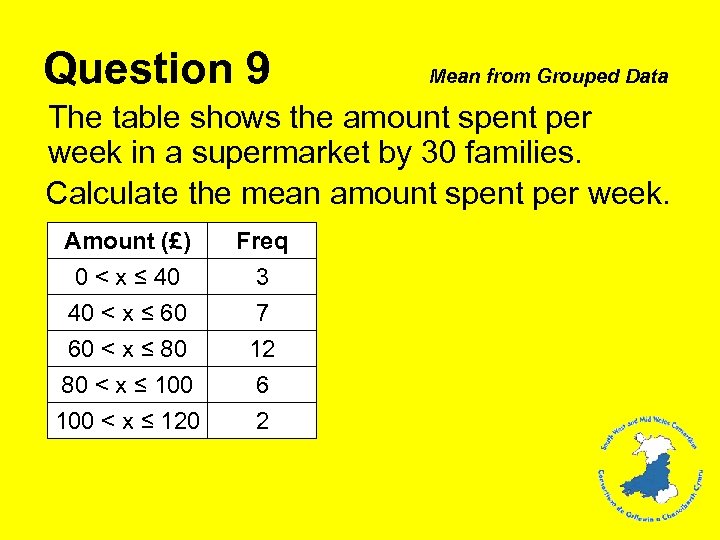 Question 9 Mean from Grouped Data The table shows the amount spent per week in a supermarket by 30 families. Calculate the mean amount spent per week. Amount (£) 0 < x ≤ 40 40 < x ≤ 60 60 < x ≤ 80 Freq 3 7 12 80 < x ≤ 100 < x ≤ 120 6 2
Question 9 Mean from Grouped Data The table shows the amount spent per week in a supermarket by 30 families. Calculate the mean amount spent per week. Amount (£) 0 < x ≤ 40 40 < x ≤ 60 60 < x ≤ 80 Freq 3 7 12 80 < x ≤ 100 < x ≤ 120 6 2
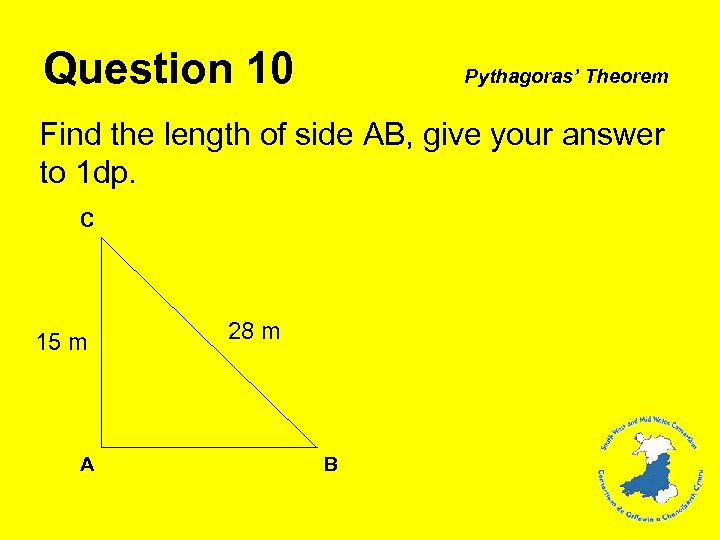 Question 10 Pythagoras’ Theorem Find the length of side AB, give your answer to 1 dp. C 15 m A 28 m B
Question 10 Pythagoras’ Theorem Find the length of side AB, give your answer to 1 dp. C 15 m A 28 m B
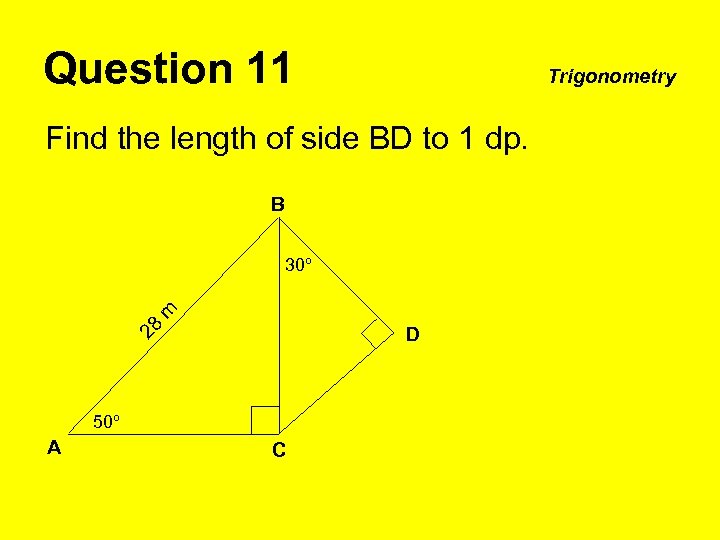 Question 11 Trigonometry Find the length of side BD to 1 dp. B m 30º 28 D 50º A C
Question 11 Trigonometry Find the length of side BD to 1 dp. B m 30º 28 D 50º A C
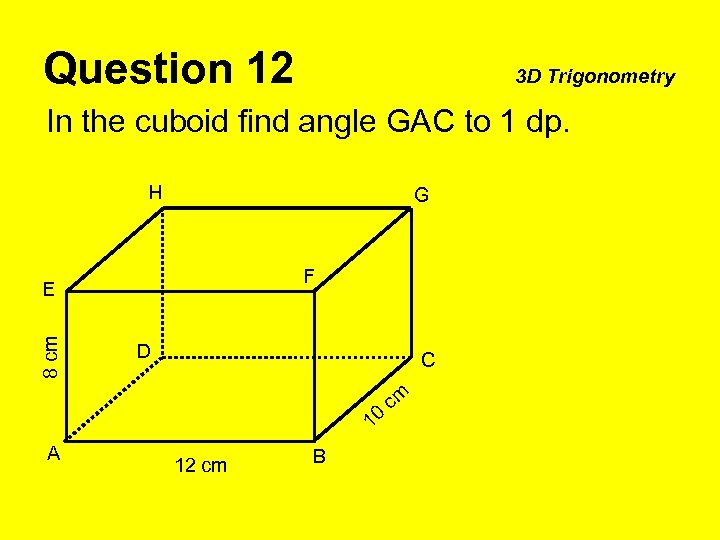 Question 12 3 D Trigonometry In the cuboid find angle GAC to 1 dp. H G F 8 cm E D C m c 0 1 A 12 cm B
Question 12 3 D Trigonometry In the cuboid find angle GAC to 1 dp. H G F 8 cm E D C m c 0 1 A 12 cm B
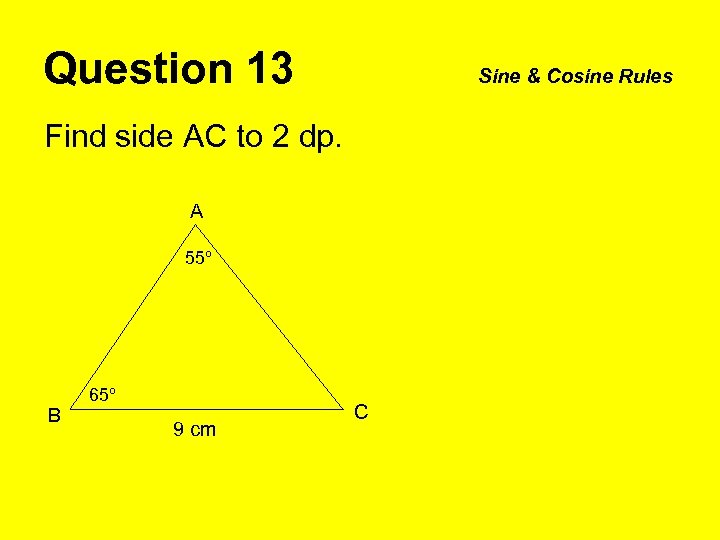 Question 13 Sine & Cosine Rules Find side AC to 2 dp. A 55º B 65º 9 cm C
Question 13 Sine & Cosine Rules Find side AC to 2 dp. A 55º B 65º 9 cm C
 Question 14 Expanding Brackets Expand simplify the following: (i) 2(4 x + 5) – 3(x – 2) (ii) (x + 6)(x – 7)
Question 14 Expanding Brackets Expand simplify the following: (i) 2(4 x + 5) – 3(x – 2) (ii) (x + 6)(x – 7)
 Question 15 Algebraic Problem – Linear The rectangle has a perimeter of 28 cm. Form an equation and solve it to find x. 3 x + 4 2 x
Question 15 Algebraic Problem – Linear The rectangle has a perimeter of 28 cm. Form an equation and solve it to find x. 3 x + 4 2 x
 Question 16 Simplify: (i) (2 – √ 3 )² Rationalise the denominator (ii) 12 √ 3 Surds
Question 16 Simplify: (i) (2 – √ 3 )² Rationalise the denominator (ii) 12 √ 3 Surds
 Question 17 Quadratic – Forming Expressions The rectangle has an area of 30 cm². Show that it satisfies the equation: 2 x² – 7 x – 45 = 0 2 x + 3 x - 5
Question 17 Quadratic – Forming Expressions The rectangle has an area of 30 cm². Show that it satisfies the equation: 2 x² – 7 x – 45 = 0 2 x + 3 x - 5
 Question 18 Solve 2 x² – 7 x – 45 = 0 giving your answers to 2 dp. Quadratic – Formula
Question 18 Solve 2 x² – 7 x – 45 = 0 giving your answers to 2 dp. Quadratic – Formula
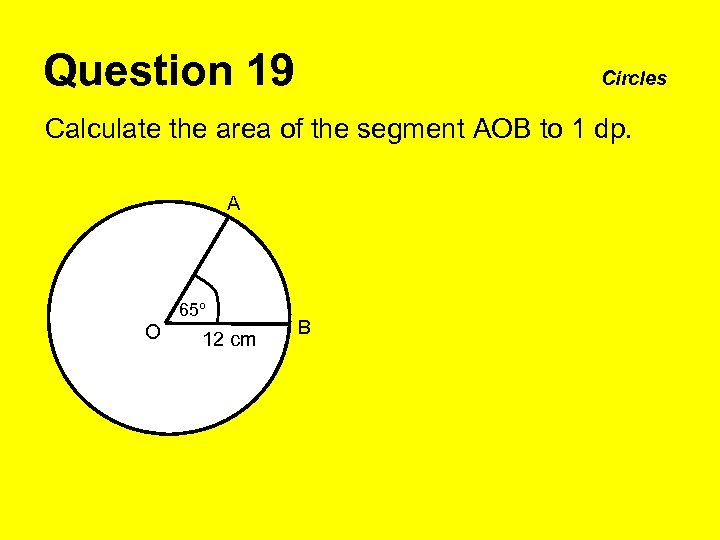 Question 19 Circles Calculate the area of the segment AOB to 1 dp. A 65º O 12 cm B
Question 19 Circles Calculate the area of the segment AOB to 1 dp. A 65º O 12 cm B
 Question 20 A sphere has a volume of 3000 cm³. Calculate its radius to 2 dp. Volume
Question 20 A sphere has a volume of 3000 cm³. Calculate its radius to 2 dp. Volume
 End of Assessment
End of Assessment
 Answers
Answers
 Question 1 (i) Find the value of: (give your answer to 1 dp) Using a Calculator 7. 8 12. 5 – 6. 8 1. 368421053 = 1. 4 (1 dp) (ii) Find the value of: (give your answer to 3 sf) √ 2. 7³ – 15. 3 2. 093561559 = 2. 09 (3 sf)
Question 1 (i) Find the value of: (give your answer to 1 dp) Using a Calculator 7. 8 12. 5 – 6. 8 1. 368421053 = 1. 4 (1 dp) (ii) Find the value of: (give your answer to 3 sf) √ 2. 7³ – 15. 3 2. 093561559 = 2. 09 (3 sf)
 Question 2 Standard Form Use you calculator to work out the value of the following, giving your answers in standard form. (i) 2. 71 × 106 – 4. 8 × 105 2, 230, 000 = 2. 23 × 106 (ii) 3. 4 × 106 ÷ 1. 7 × 10 -2 200, 000 = 2 × 108
Question 2 Standard Form Use you calculator to work out the value of the following, giving your answers in standard form. (i) 2. 71 × 106 – 4. 8 × 105 2, 230, 000 = 2. 23 × 106 (ii) 3. 4 × 106 ÷ 1. 7 × 10 -2 200, 000 = 2 × 108
 Question 3 Trial & Improvement Solve by Trial & Improvement to 1 dp: x³ + 4 x = 48 x = 3 x = 4 x = 3. 2 x = 3. 3 (3)³ + 4(3) = 39 (4)³ + 4(4) = 80 (3. 2)³ + 4(3. 2) = 45. 568 (3. 3)³ + 4(3. 3) = 49. 137 Closest 1 dp guess x = 3. 3 (1 dp) too small too big
Question 3 Trial & Improvement Solve by Trial & Improvement to 1 dp: x³ + 4 x = 48 x = 3 x = 4 x = 3. 2 x = 3. 3 (3)³ + 4(3) = 39 (4)³ + 4(4) = 80 (3. 2)³ + 4(3. 2) = 45. 568 (3. 3)³ + 4(3. 3) = 49. 137 Closest 1 dp guess x = 3. 3 (1 dp) too small too big
 Question 4 % Change A house’s value decreases from £ 165, 000 to £ 130, 000. Find the % decrease in its value to the nearest %. % Change = Change × 100 Original % Change = 35, 000 × 100 165, 000 = 21%
Question 4 % Change A house’s value decreases from £ 165, 000 to £ 130, 000. Find the % decrease in its value to the nearest %. % Change = Change × 100 Original % Change = 35, 000 × 100 165, 000 = 21%
 Question 5 % – Compound Interest A person invests £ 5, 000 for 3 years at a rate of 3. 75% per annum. Calculate the value of their investment after the 3 years. 1 st year 3. 75 × £ 5000 = £ 187. 50 100 2 nd year 3. 75 × £ 5187. 50 = £ 194. 53 100 3 rd year Value: £ 5187. 50 Value: £ 5382. 03 3. 75 × £ 5382. 03 = £ 201. 83 100 Final Value: £ 5583. 86
Question 5 % – Compound Interest A person invests £ 5, 000 for 3 years at a rate of 3. 75% per annum. Calculate the value of their investment after the 3 years. 1 st year 3. 75 × £ 5000 = £ 187. 50 100 2 nd year 3. 75 × £ 5187. 50 = £ 194. 53 100 3 rd year Value: £ 5187. 50 Value: £ 5382. 03 3. 75 × £ 5382. 03 = £ 201. 83 100 Final Value: £ 5583. 86
 Question 6 % – Finding the Original A leather settee is reduced in a sale by 30%. It now costs £ 595. Calculate the price of the settee before the reduction. 100% = Original Price 70% = New Price 70% = £ 595 1% = £ 8. 50 100% = £ 850 (595 ÷ 70) (8. 5 × 100)
Question 6 % – Finding the Original A leather settee is reduced in a sale by 30%. It now costs £ 595. Calculate the price of the settee before the reduction. 100% = Original Price 70% = New Price 70% = £ 595 1% = £ 8. 50 100% = £ 850 (595 ÷ 70) (8. 5 × 100)
 Question 7 Nth Term & Sequences (i) Find the Nth term in the following sequence: 1 2 3 4 5 N th 1, 4, 7, 10, 13 3 n – 2 (ii) What would the 20 th term be? 3(20) - 2 60 - 2 58 ?
Question 7 Nth Term & Sequences (i) Find the Nth term in the following sequence: 1 2 3 4 5 N th 1, 4, 7, 10, 13 3 n – 2 (ii) What would the 20 th term be? 3(20) - 2 60 - 2 58 ?
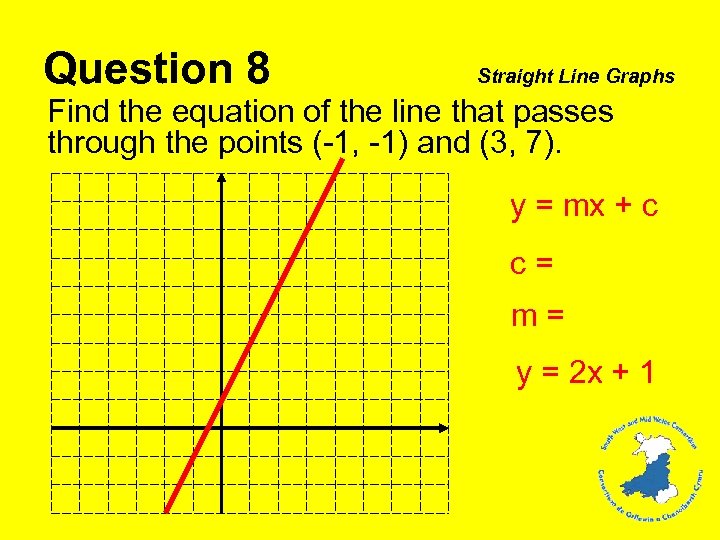 Question 8 Straight Line Graphs Find the equation of the line that passes through the points (-1, -1) and (3, 7). y = mx + c c = m = y = 2 x + 1
Question 8 Straight Line Graphs Find the equation of the line that passes through the points (-1, -1) and (3, 7). y = mx + c c = m = y = 2 x + 1
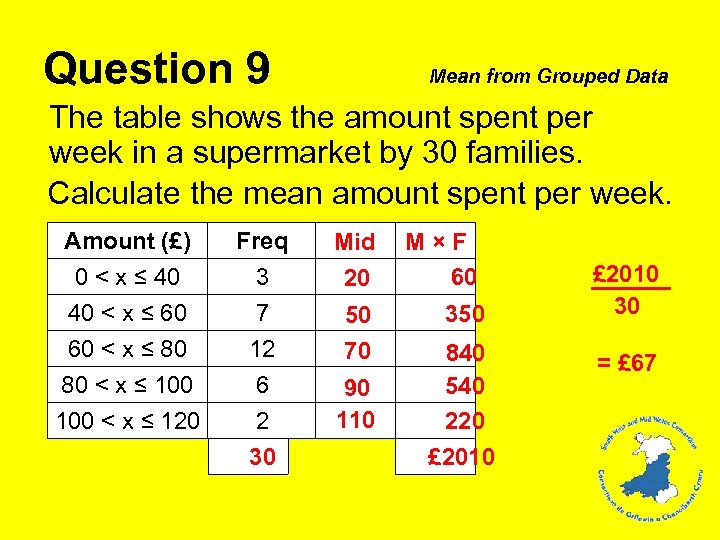 Question 9 Mean from Grouped Data The table shows the amount spent per week in a supermarket by 30 families. Calculate the mean amount spent per week. Amount (£) 0 < x ≤ 40 40 < x ≤ 60 60 < x ≤ 80 Freq 3 7 12 Mid 20 50 70 80 < x ≤ 100 < x ≤ 120 6 2 30 90 110 M×F 60 350 840 540 220 £ 2010 30 = £ 67
Question 9 Mean from Grouped Data The table shows the amount spent per week in a supermarket by 30 families. Calculate the mean amount spent per week. Amount (£) 0 < x ≤ 40 40 < x ≤ 60 60 < x ≤ 80 Freq 3 7 12 Mid 20 50 70 80 < x ≤ 100 < x ≤ 120 6 2 30 90 110 M×F 60 350 840 540 220 £ 2010 30 = £ 67
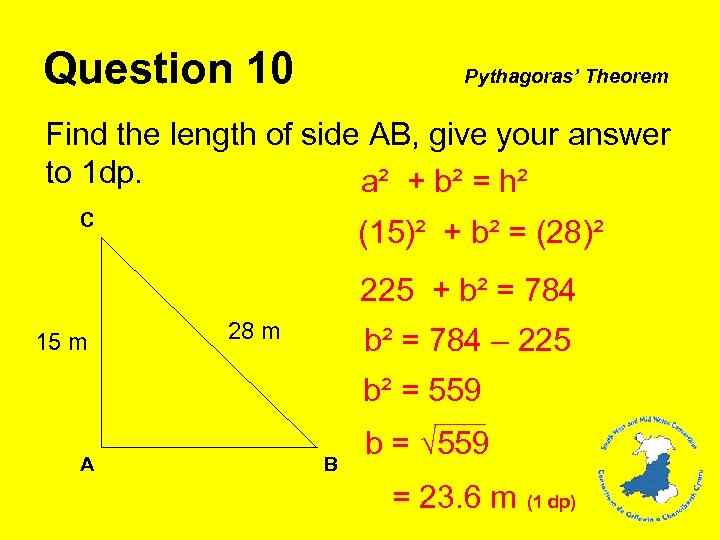 Question 10 Pythagoras’ Theorem Find the length of side AB, give your answer to 1 dp. a² + b² = h² C (15)² + b² = (28)² 225 + b² = 784 15 m 28 m b² = 784 – 225 b² = 559 A B b = √ 559 = 23. 6 m (1 dp)
Question 10 Pythagoras’ Theorem Find the length of side AB, give your answer to 1 dp. a² + b² = h² C (15)² + b² = (28)² 225 + b² = 784 15 m 28 m b² = 784 – 225 b² = 559 A B b = √ 559 = 23. 6 m (1 dp)
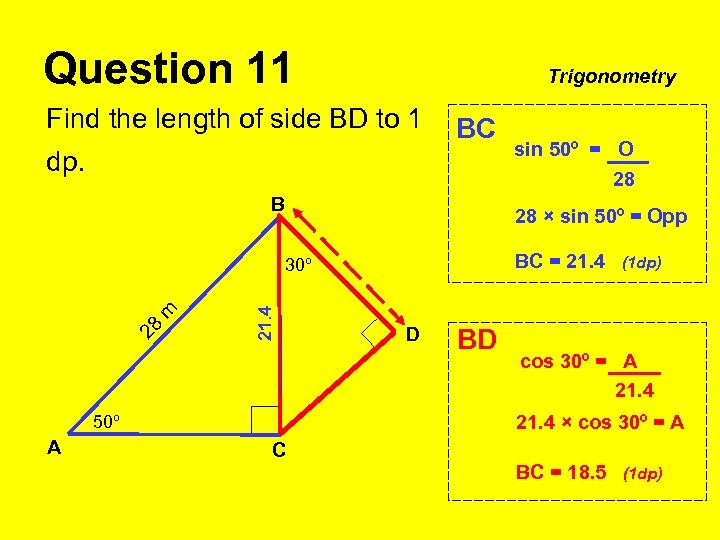 Question 11 Trigonometry Find the length of side BD to 1 BC dp. B 28 × sin 50º = Opp BC = 21. 4 28 m 30º D BD (1 dp) cos 30º = A 21. 4 × cos 30º = A 50º A sin 50º = O 28 C BC = 18. 5 (1 dp)
Question 11 Trigonometry Find the length of side BD to 1 BC dp. B 28 × sin 50º = Opp BC = 21. 4 28 m 30º D BD (1 dp) cos 30º = A 21. 4 × cos 30º = A 50º A sin 50º = O 28 C BC = 18. 5 (1 dp)
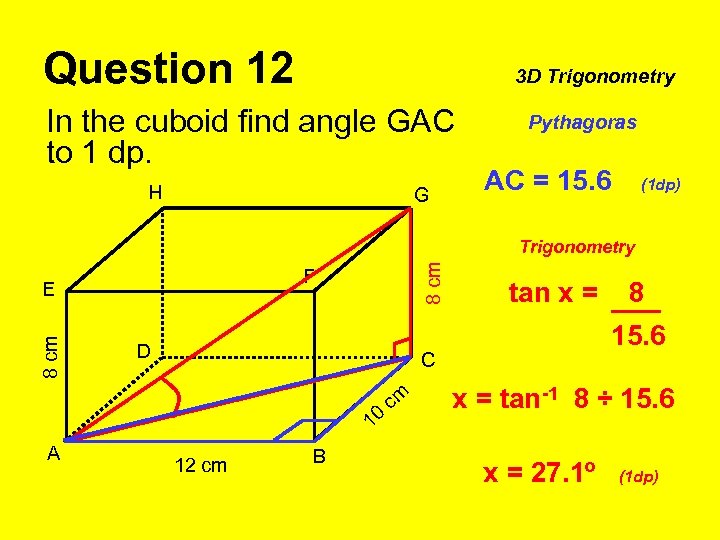 Question 12 3 D Trigonometry In the cuboid find angle GAC to 1 dp. H G Pythagoras AC = 15. 6 (1 dp) F E 8 cm Trigonometry D m 1 12 cm B 8 15. 6 C c 0 A tan x = tan-1 8 ÷ 15. 6 x = 27. 1º (1 dp)
Question 12 3 D Trigonometry In the cuboid find angle GAC to 1 dp. H G Pythagoras AC = 15. 6 (1 dp) F E 8 cm Trigonometry D m 1 12 cm B 8 15. 6 C c 0 A tan x = tan-1 8 ÷ 15. 6 x = 27. 1º (1 dp)
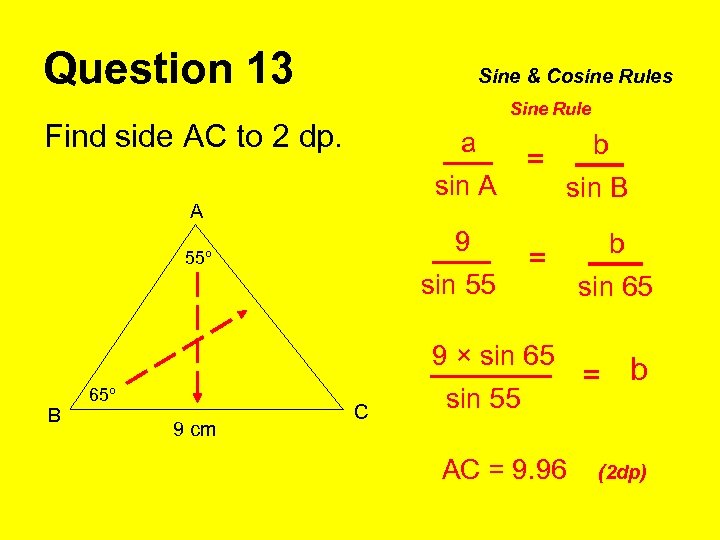 Question 13 Sine & Cosine Rules Sine Rule Find side AC to 2 dp. a sin A A 9 55º sin 55 = b sin B = 9 × sin 65 B 65º 9 cm C sin 55 AC = 9. 96 b sin 65 = b (2 dp)
Question 13 Sine & Cosine Rules Sine Rule Find side AC to 2 dp. a sin A A 9 55º sin 55 = b sin B = 9 × sin 65 B 65º 9 cm C sin 55 AC = 9. 96 b sin 65 = b (2 dp)
 Question 14 Expanding Brackets Expand simplify the following: (i) 2(4 x + 5) – 3(x – 2) (ii) (x + 6)(x – 7) 5 x +16 x² – x – 42
Question 14 Expanding Brackets Expand simplify the following: (i) 2(4 x + 5) – 3(x – 2) (ii) (x + 6)(x – 7) 5 x +16 x² – x – 42
 Question 15 Algebraic Problem – Linear The rectangle has a perimeter of 28 cm. Form an equation and solve it to find x. 3 x + 4 10 x + 8 = 28 2 x x = 2
Question 15 Algebraic Problem – Linear The rectangle has a perimeter of 28 cm. Form an equation and solve it to find x. 3 x + 4 10 x + 8 = 28 2 x x = 2
 Question 16 Simplify: (i) (2 – √ 3 )² Surds 7 - 4√ 3 Rationalise the denominator (ii) 12 √ 3 4 √ 3
Question 16 Simplify: (i) (2 – √ 3 )² Surds 7 - 4√ 3 Rationalise the denominator (ii) 12 √ 3 4 √ 3
 Question 17 Quadratic – Forming Expressions The rectangle has an area of 30 cm². Show that it satisfies the equation: 2 x² – 7 x – 45 = 0 2 x + 3 x - 5 Area = L × W (2 x + 3)(x - 5) = 30 2 x² - 10 x + 3 x - 15 = 30 2 x² - 7 x - 15 - 30 = 0 2 x² - 7 x - 45 = 0
Question 17 Quadratic – Forming Expressions The rectangle has an area of 30 cm². Show that it satisfies the equation: 2 x² – 7 x – 45 = 0 2 x + 3 x - 5 Area = L × W (2 x + 3)(x - 5) = 30 2 x² - 10 x + 3 x - 15 = 30 2 x² - 7 x - 15 - 30 = 0 2 x² - 7 x - 45 = 0
 Question 18 Solve Quadratic – Formula a = 2 2 x² – 7 x – 45 = 0 b = – 7 c = – 45 giving your answers to 2 dp. - b ± √b² - 4 ac 2 a -- 7 ± √(-7)² - 4(2)(-45) 2(2) + 7 ± √ 49 -- 360 4 7 ± √ 409 4 1 st Soln 7 + √ 409 = 6. 81 (2 dp) 4 n 2 nd Sol 7 – √ 409 4 = -3. 31 (2 dp)
Question 18 Solve Quadratic – Formula a = 2 2 x² – 7 x – 45 = 0 b = – 7 c = – 45 giving your answers to 2 dp. - b ± √b² - 4 ac 2 a -- 7 ± √(-7)² - 4(2)(-45) 2(2) + 7 ± √ 49 -- 360 4 7 ± √ 409 4 1 st Soln 7 + √ 409 = 6. 81 (2 dp) 4 n 2 nd Sol 7 – √ 409 4 = -3. 31 (2 dp)
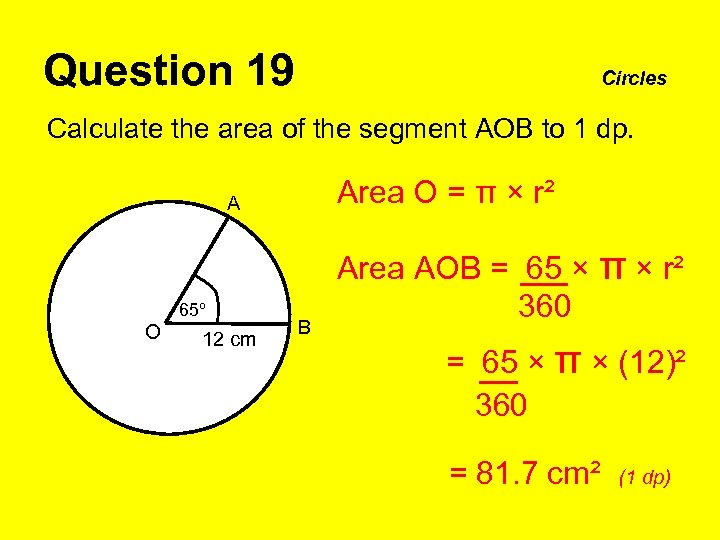 Question 19 Circles Calculate the area of the segment AOB to 1 dp. Area O = π × r² A 65º O 12 cm B Area AOB = 65 × π × r² 360 = 65 × π × (12)² 360 = 81. 7 cm² (1 dp)
Question 19 Circles Calculate the area of the segment AOB to 1 dp. Area O = π × r² A 65º O 12 cm B Area AOB = 65 × π × r² 360 = 65 × π × (12)² 360 = 81. 7 cm² (1 dp)
 Question 20 Volume A sphere has a volume of 3000 cm³. Calculate its radius to 2 dp. Vol = 43 × π × r³ 3000 × 3 = r³ 4 × π r³ = 716. 2 r = 716. 2 = 8. 95 cm (2 dp) 3
Question 20 Volume A sphere has a volume of 3000 cm³. Calculate its radius to 2 dp. Vol = 43 × π × r³ 3000 × 3 = r³ 4 × π r³ = 716. 2 r = 716. 2 = 8. 95 cm (2 dp) 3


