Гармонический осциллятор Семинар 7
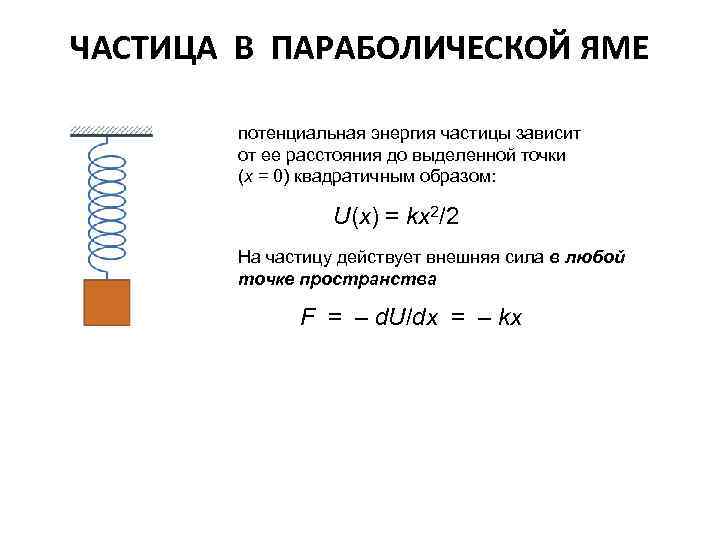
ЧАСТИЦА В ПАРАБОЛИЧЕСКОЙ ЯМЕ потенциальная энергия частицы зависит от ее расстояния до выделенной точки (х = 0) квадратичным образом: U(x) = kx 2/2 На частицу действует внешняя сила в любой точке пространства F = – d. U/dx = – kx
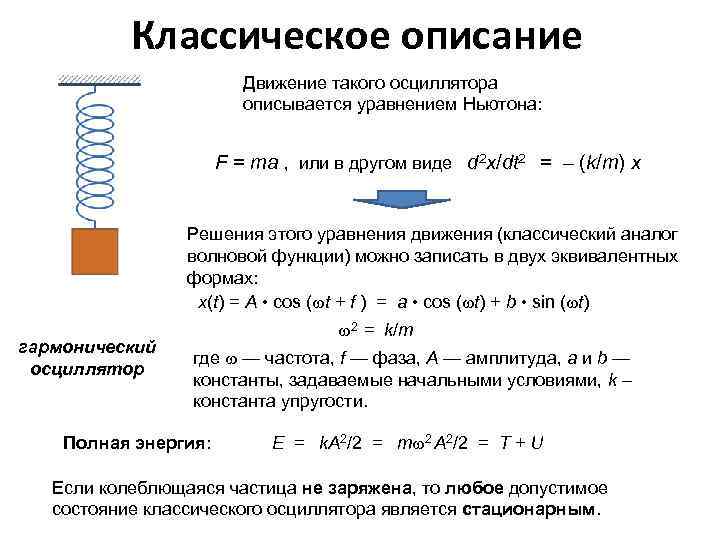
Классическое описание Движение такого осциллятора описывается уравнением Ньютона: F = ma , или в другом виде d 2 x/dt 2 = – (k/m) x Решения этого уравнения движения (классический аналог волновой функции) можно записать в двух эквивалентных формах: x(t) = A • cos ( t + f ) = a • cos ( t) + b • sin ( t) гармонический осциллятор 2 = k/m где — частота, f — фаза, А — амплитуда, а и b — константы, задаваемые начальными условиями, k – константа упругости. Полная энергия: Е = k. A 2/2 = m 2 A 2/2 = Т + U Если колеблющаяся частица не заряжена, то любое допустимое состояние классического осциллятора является стационарным.
Квантовомеханическое описание Квантовомеханические состояния осциллятора должны описываться волновыми функциями, зависящими от времени и одной пространственной переменной. Среди них имеются и стационарные: Ф(x, t) = Ф(x) • e i(E/h)t Стационарное уравнение Шредингера С целью упрощения произведем некоторые преобразования, которые сводятся к следующему: а) вместо независимой переменной х берется другая мера расстояния = ( )1/2 • х , где = m / h при этом функция Ф(х) переходит в функцию Ф( ), б) вместо энергии Е берется другая мера энергии = (2 m / h 2) • E.
Волновая функция теперь приобретает более простой вид: Ф( ) = N • exp(– 2/2) • H( ) Нормировочный множитель Экспоненциальный Множитель (один для всех решений) Степенной множитель (для каждого решения свой) уравнение для степенного множителя Уравнение Эрмита его решения: Полиномы Эрмита Нv ( ) = (– 1)v • exp ( 2) • dv [exp (– 2)]/d v Н 0 = 1; H 1 = 2 ; H 2 = 4 2 – 2; H 3 = 8 3 – 12 Н v + 1 = 2 • Н v – 2 v • H v – 1 и т. д.
Видно, что функции, описывающие стационарные состояния осциллятора, образуют дискретный набор, нумеруемый квантовым числом v, которое называется колебательным квантовым числом и может принимать любые целые значения от 0 до бесконечности: v = 0, 1, 2, … выражение для нормировочного множителя: где v — квантовое число, а ! — знак операции факториала. Через это квантовое число v можно также рассчитать и энергию соответствующего стационарного состояния: Еv = h (v + 1/2)
Энергетическая диаграмма нулевая энергия
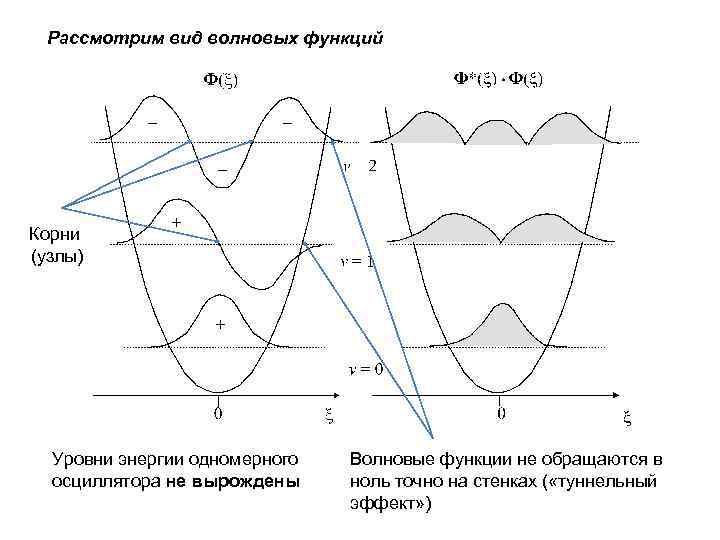
Рассмотрим вид волновых функций Корни (узлы) Уровни энергии одномерного осциллятора не вырождены Волновые функции не обращаются в ноль точно на стенках ( «туннельный эффект» )
Многомерный осциллятор В большинстве реальных структур возможно не одно, а множество различных типов колебаний. Колебательное движение сложной системы модель многомерного осциллятора совокупность (наложение, суперпозицию) независимых друг от друга одномерных колебаний, которые называются нормальными. 1) участвуют все атомы молекулы, 2) все атомы колеблются в одной и той же частотой и фазой. Ф( 1 , 2 , . . . n ) = Ф 1( 1) Ф 2( 2). . . Фn( n) Е = Е 1 + Е 2 +. . + Еn = h 1(v 1 + 1/2) + h 2(v 2 + 1/2) +. . . Число нормальных колебаний (n) зависит от числа атомов (N) в молекуле и равно n = 3 N – 6 (для нелинейных молекул) или n = 3 N – 5 (для линейных молекул).
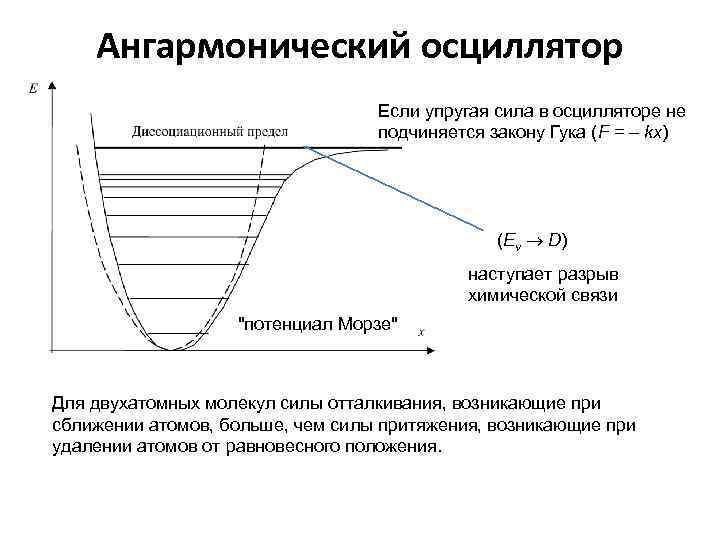
Ангармонический осциллятор Если упругая сила в осцилляторе не подчиняется закону Гука (F = – kx) (Еv D) наступает разрыв химической связи "потенциал Морзе" Для двухатомных молекул силы отталкивания, возникающие при сближении атомов, больше, чем силы притяжения, возникающие при удалении атомов от равновесного положения.
Скачать презентацию Гармонический осциллятор Семинар 7 ЧАСТИЦА В ПАРАБОЛИЧЕСКОЙ
07_oscillator.ppt