ГАРМОНИЧЕСКИЕ ВОЛНОВЫЕ ПОЛЯ ПЛОСКИЕ ОДНОРОДНЫЕ И НЕОДНОРОДНЫЕ ВОЛНЫ

ГАРМОНИЧЕСКИЕ ВОЛНОВЫЕ ПОЛЯ. ПЛОСКИЕ ОДНОРОДНЫЕ И НЕОДНОРОДНЫЕ ВОЛНЫ

Волновое уравнение Гельмгольца В физике и технике распространен спектральный подход к изучению волновых явлений. Этот метод позволяет свести анализ поведения волн к анализу поведения «гармонических» волн. И решение волнового уравнения записывается в виде:

Волновое уравнение Гельмгольца Поскольку дифференцирование такого вида по t сводится к умножению на j , то при подстановке этих обозначений в волновое уравнение Даламбера мы получим волновое уравнение Гельмгольца: уравнение Гельмгольца где волновые числа:

Волновое уравнение Гельмгольца Решение запишется в виде Где r – расстояние от источника в направлении распространения луча. Мы имеем волну, гармоническую во времени и пространстве, модуль волнового вектора. - постоянная величина, численно равна амплитуде на единичном расстоянии от источника.

Волновое уравнение Гельмгольца • Разложение сложного волнового процесса на гармонические волны и сведение задачи к уравнению Гельмгольца, где частота считается уже заданной, очень удобно. • Волновой вектор равен по модулю волновому числу k и имеет направление нормали к волновой поверхности.

Решение уравнения Гельмгольца. Плоские однородные и неоднородные волны Подставим решение в уравнение Гельмгольца для простоты опускаем то, что идет под знаком экспоненты отсюда мы имеем т. е. функция такого вида является решением, если аргумент удовлетворяет этому условию

Решение уравнения Гельмгольца. Плоские однородные и неоднородные волны Пусть смещение имеет компоненту OXZ, волна поляризована вертикально, тогда т. е. при k=const для любого k найдется Возможно два случая: 1) , то - действительное число и 2) , то и Такая волна называется неоднородной плоской волной. выбор знака определяется соображением

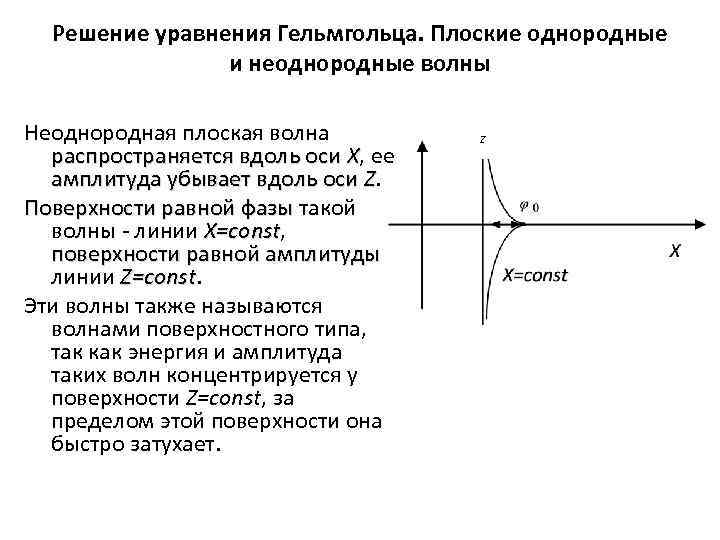Решение уравнения Гельмгольца. Плоские однородные и неоднородные волны Неоднородная плоская волна распространяется вдоль оси X, ее амплитуда убывает вдоль оси Z. Поверхности равной фазы такой волны - линии X=const, const поверхности равной амплитуды линии Z=const Эти волны также называются волнами поверхностного типа, так как энергия и амплитуда таких волн концентрируется у поверхности Z=const, за пределом этой поверхности она быстро затухает. Z

Решение уравнения Гельмгольца. Плоские однородные и неоднородные волны Т. к. kx k, Cx C, где Сx - фазовая скорость распространения плоских волн. Из последнего соотношения видно, что скорость убывания волны по Z определяется длиной волны : чем меньше длина волны, тем скорее амплитуда волны уменьшается при удалении от плоскости Z=0.

Поле смещений для плоских однородных и неоднородных волн Поле смещений плоской однородной волны имеет вид: Вектор параллелен , т. е. частицы смещаются в направлении, совпадающем с нормалью к фронту (волна имеет линейную поляризацию).

Поле смещений для плоских однородных и неоднородных волн Потенциал плоской неоднородной волны может быть записан в виде: Поле смещений плоских неоднородных волн можно записать следующим образом: Где

Поле смещений для плоских однородных и неоднородных волн Вспомним из ТФКП, как определяются величины: действительные части компонент смещения частиц будут выражаться: Разделим их на коэффициенты A и B. отсюда

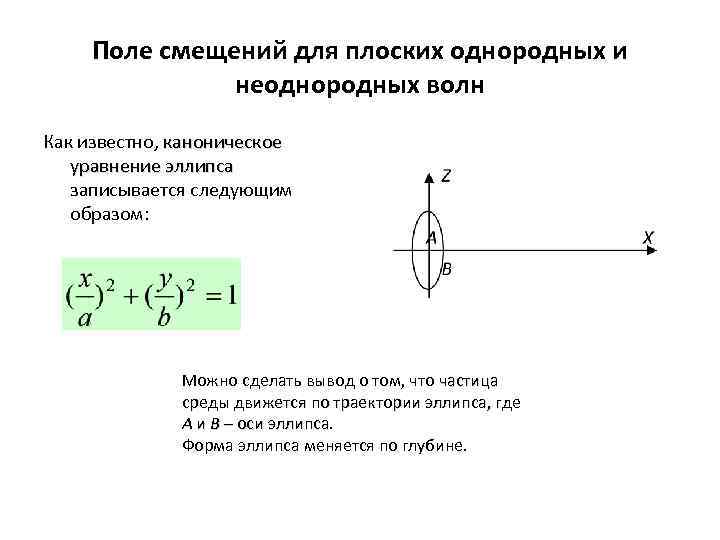Поле смещений для плоских однородных и неоднородных волн Как известно, каноническое уравнение эллипса записывается следующим образом: Можно сделать вывод о том, что частица среды движется по траектории эллипса, где A и B – оси эллипса Форма эллипса меняется по глубине.

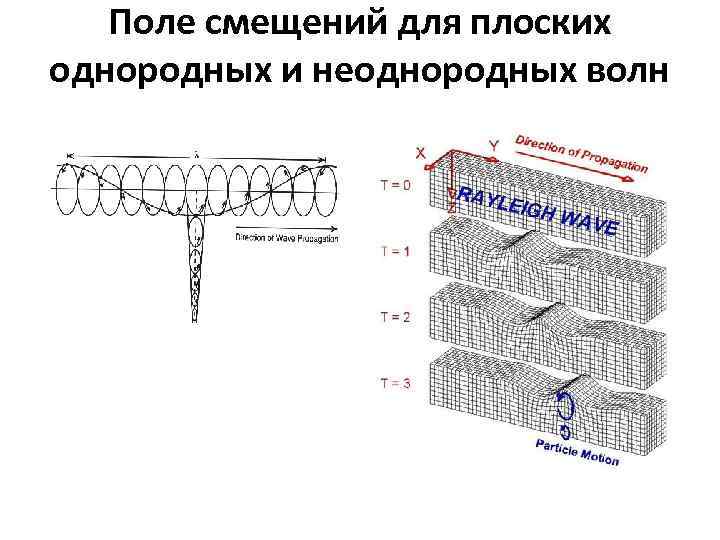
Поле смещений для плоских однородных и неоднородных волн В качестве примера неоднородных плоских волн можно привести волну Релея, которая распространяется вдоль свободной границы. Поверхностные волны Рэлея имеют эллиптическую поляризацию. При этом вертикальная компонента по абсолютной величине всегда больше горизонтальной. Рэлеевские волны обладают малыми скоростями и низкими частотами. Волна Релея вызывает одновременно деформацию объема и сдвига, и ее сдвига интенсивность экспоненциально убывает с удалением от поверхности, так что она практически существует поверхности только в слое толщиной порядка длины волны. Поэтому чем больше длина волны, т. е. ниже частота колебаний, тем глубже они проникают внутрь среды

Поле смещений для плоских однородных и неоднородных волн Скорость VR зависит от соотношения Vs/Vp, т. е. от коэффициента Пуассона. Однако эта зависимость проявляется слабо. При изменении величины Vs/Vp в допустимых пределах (0 -0, 7) отношение VR/VS изменяется от 0, 87 до 0, 96. Можно считать, что волна Релея распространяется вдоль свободной поверхности полупространства со скоростью VR = 0, 9 Vs. Скорость ее в однородной среде не зависит от частоты колебаний Это означает, что волна Релея, образующаяся на свободной границе абсолютно упругого полупространства, не имеет частотной дисперсии. Вблизи земной поверхности, особенно у дисперсии подошвы ЗМС, упругие постоянные испытывают значительные изменения, поэтому скорость волн Рэлея меняется с изменением длины волны, волны диспергируют и форма волнового пакета в процессе распространения меняется. Поскольку поверхностные волны характеризуются большими амплитудами, необходимо производить заглубление источника при возбуждении

Поле смещений для плоских однородных и неоднородных волн

Что такое гармонические волновые поля? Что такое волновое число? Что такое неоднородная плоская волна? По какой траектории происходит движение частицы при распространении неоднородной плоской волны? • Для чего необходимо заглублять источник при возбуждении? • •