Game Theory Topic 3 Sequential Games It is

Game Theory Topic 3 Sequential Games “It is true that life must be understood backward, but … it must be lived forward. ” - Søren Kierkegaard

Review Understanding the outcomes of games n Sometimes easy n q Dominant n Sometimes more challenging q “I n strategies know that you know …” What if a game is sequential? q Market entry 2 Mike Shor

Very Large Airplanes: Airbus vs. Boeing n Industry background q “ The problem is the monopoly of the 747 … They have a product. We have none. ” - Airbus Executive n Industry feasibility studies: q n Room for at most one megaseater Airbus q Initiated plans to build a super-jumbo jet 3 Mike Shor

Very Large Airplanes: Airbus vs. Boeing n Boeing reaction “Boeing, the world’s top aircraft maker, announced it was building a plane with 600 to 800 seats, the biggest and most expensive airliner ever. ” - Business. Week 4 Mike Shor

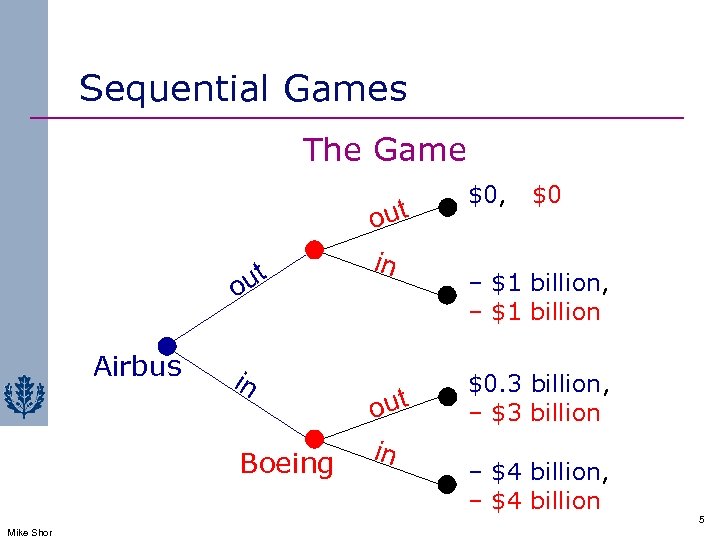Sequential Games The Game ut o Airbus in Boeing out in $0, $0 – $1 billion, – $1 billion $0. 3 billion, – $3 billion – $4 billion, – $4 billion 5 Mike Shor

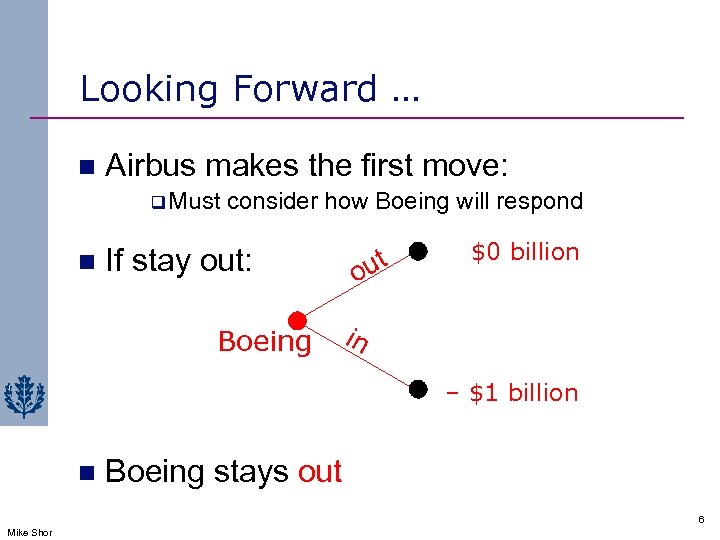Looking Forward … n Airbus makes the first move: q Must n consider how Boeing will respond If stay out: Boeing ut o $0 billion in – $1 billion n Boeing stays out 6 Mike Shor

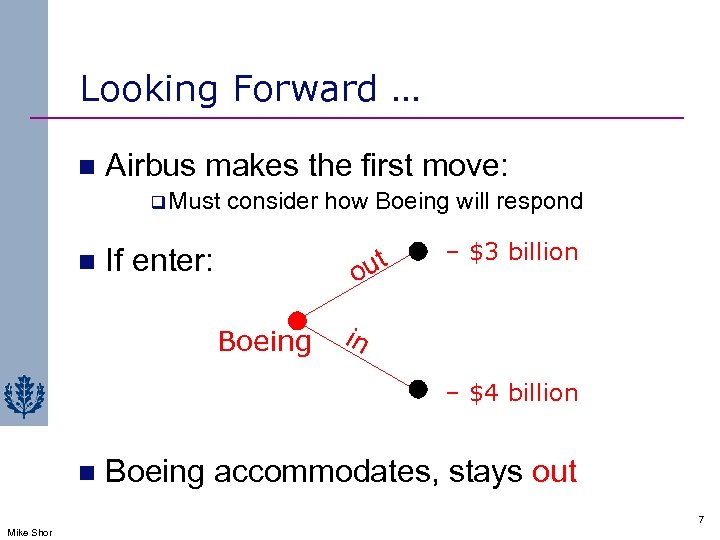Looking Forward … n Airbus makes the first move: q Must n consider how Boeing will respond If enter: ut o Boeing – $3 billion in – $4 billion n Boeing accommodates, stays out 7 Mike Shor

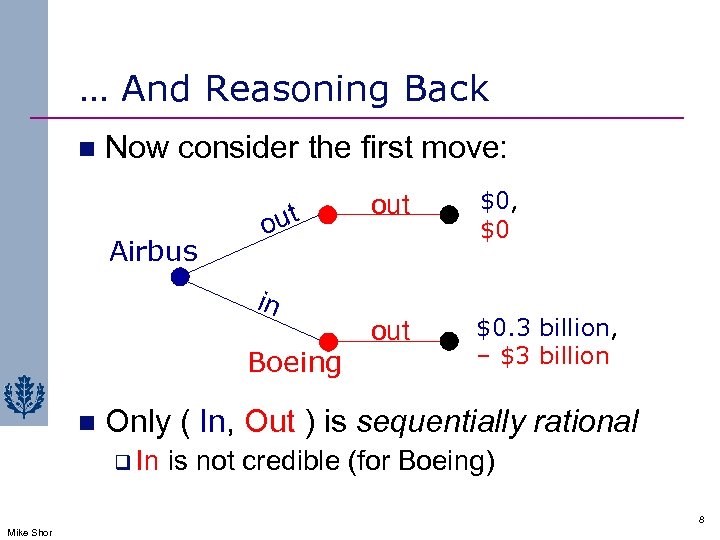… And Reasoning Back n Now consider the first move: Airbus out in Boeing n out $0, $0 out $0. 3 billion, – $3 billion Only ( In, Out ) is sequentially rational q In is not credible (for Boeing) 8 Mike Shor

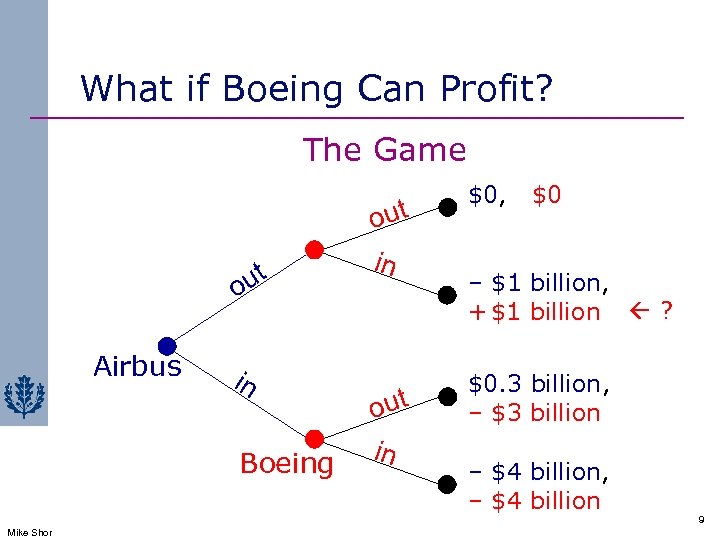What if Boeing Can Profit? The Game ut o Airbus in Boeing out in $0, $0 – $1 billion, + $1 billion ? $0. 3 billion, – $3 billion – $4 billion, – $4 billion 9 Mike Shor

Nash Equilibria Are Deceiving Boeing Airbus Out In Out 0 , 0 0. 3 , -3 In -1 , 1 -4 , -4 n Two equilibria (game of chicken) n But, still only one is sequentially rational 10 Mike Shor

Airbus vs. Boeing • October 2007 • A 380 enters commercial service • Singapore to Sydney • List price: $350 million • September 2011 • Four year anniversary: 12, 000 seats sold 11 Mike Shor

Solving Sequential Games n Intuitive Approach: Start at the end and trim the tree to the present q Eliminates non-credible future actions q 12 Mike Shor

Solving Sequential Games n Steps: 1. 2. 3. 4. 5. 6. 7. q q n Pick a last move What player is making the decision? What decisions are available to that player? What are that player’s payoffs from each decision? Select the highest Place an arrow on the selected branch Delete all other branches Now, treat the next-to-last player to act as last Continue in this manner until you reach the root Equilibrium: the “name” of each arrow 13 Mike Shor

Subgame Perfect Equilibrium n Subgame: q n A decision node and all nodes that follow it Subgame Perfect Equilibrium: (a. k. a. Rollback, Backwards Induction) The equilibrium specifies an action at every decision node in the game q The equilibrium is also an equilibrium in every subgame q 14 Mike Shor

Nash Equilibria Are Deceiving Player 2 Player 1 n n Mike Shor Less More X 10 , 0 20 , 20 Y 30 , 30 40 , 10 Does either player have a dominant strategy? What is the equilibrium? What if Player 1 goes first? What if Player 2 goes first? 15

Solving Sequential Games n Thinking backwards is easy in game trees q Start at the end and trim the tree to the present n Thinking backwards is challenging in practice n Outline: Strategic moves in early rounds q The rule of three (again) q Seeing the end of the game q 16 Mike Shor

Graduation Speaker Revisited Graduation speaker Bernie Sanders, Donald Trump, or Hillary Clinton? n Four committee members prefer: Bernie n (B>D>H) to Hillary to Bernie ( D > H > B) Two committee members prefer: Hillary n to Hillary Three committee members prefer: Donald n to Donald to Bernie to Donald (H>B>D) Voting by Majority Rule 17 Mike Shor

Graduation Speaker Revisited Graduation speaker Bernie Sanders, Donald Trump, or Hillary Clinton? n n Member preferences: 4 (B>D>H) 3 (D>H>B) Majority rule results: q n B beats D ; D beats H 2 (H>B>D) ; H beats B Voting results (example): q B beats D then winner versus H H 18 Mike Shor

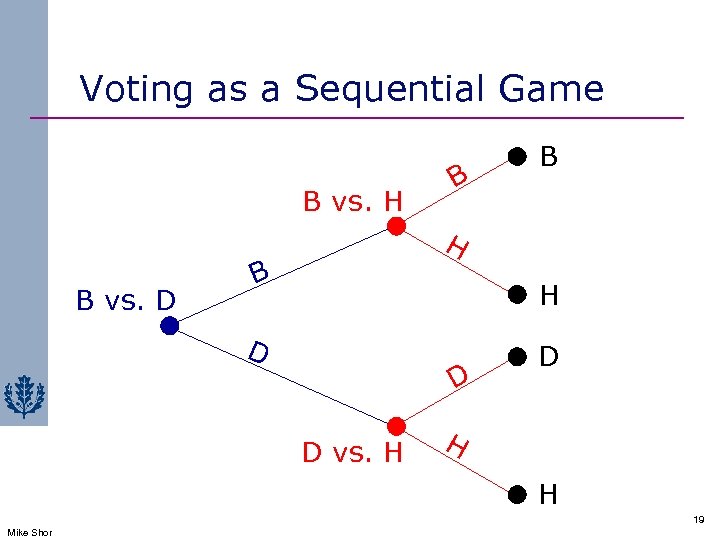Voting as a Sequential Game B vs. H B B H B vs. D B H D D D vs. H D H H 19 Mike Shor

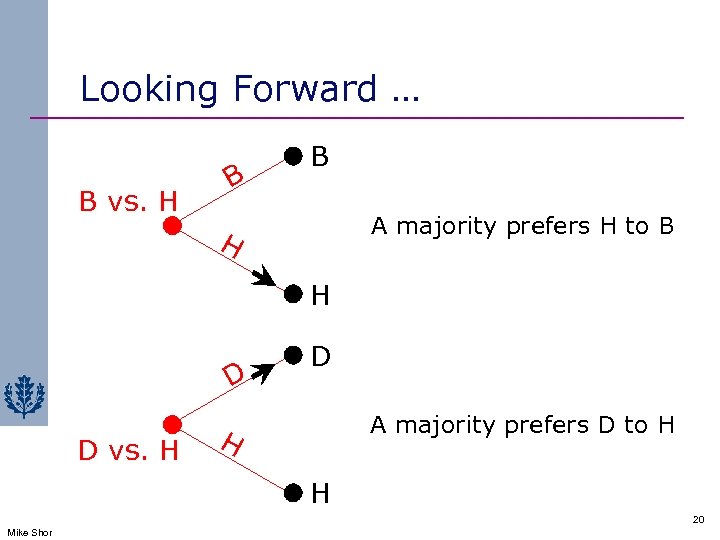Looking Forward … B vs. H B B A majority prefers H to B H H D D vs. H D A majority prefers D to H H H 20 Mike Shor

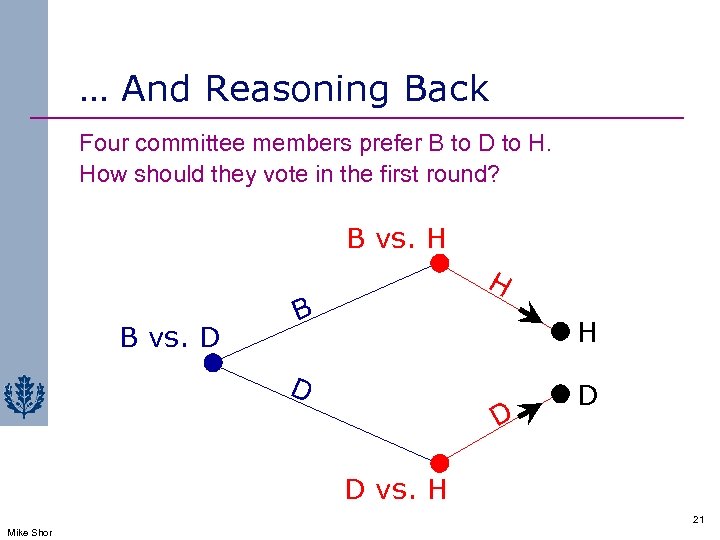… And Reasoning Back Four committee members prefer B to D to H. How should they vote in the first round? B vs. H H B vs. D B H D D vs. H 21 Mike Shor

Sequential Rationality Look forward and reason back. Anticipate what your rivals will do tomorrow in response to your actions today 22 Mike Shor

Importance of Rules n Outcome is still predetermined: q q q B D H vs. vs. D H B then winner versus H then winner versus B then winner versus D 23 Mike Shor

Accommodating a Potential Entrant n Do you enter? n Do you accommodate entry? n What if there are fifty potential entrants? 24 Mike Shor

Survivor Immunity Challenge n There are 21 flags n Players alternate removing 1, 2, or 3 flags n The player to take the last flag wins 25 Mike Shor

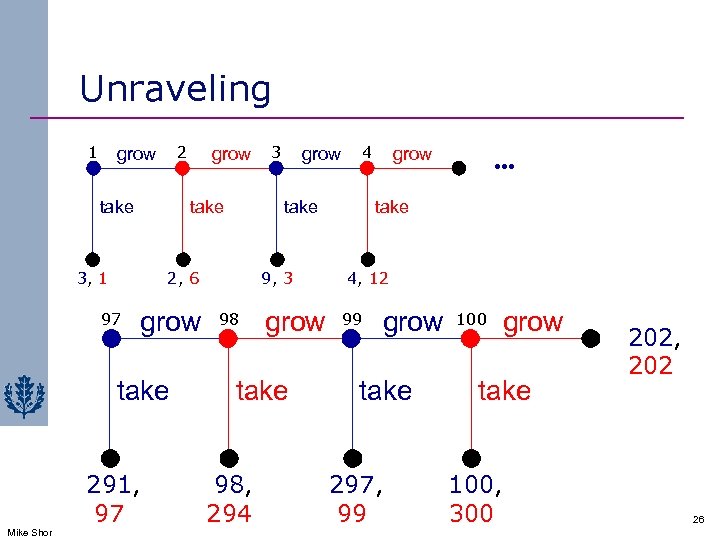Unraveling 1 2 grow take 3, 1 grow take 291, 97 3 grow 4 take 2, 6 97 Mike Shor grow take 9, 3 98 4, 12 grow 99 take 98, 294 grow take 297, 99 100 grow take 100, 300 202, 202 26

Unraveling n Equilibrium: take , take , take , … n Remember: An equilibrium specifies an action at every decision node q Even those that will not be reached in equilibrium q 27 Mike Shor

Sequential Games n n You have a monopoly market in every state There is one potential entrant in each state They make their entry decisions sequentially q Florida may enter today q New York may enter tomorrow q etc. q n n Each time, you can accommodate or fight What do you do the first year? 28 Mike Shor

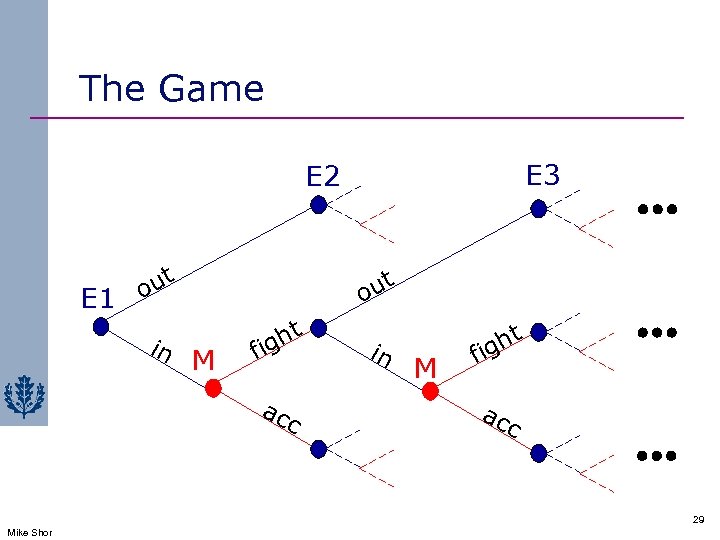The Game E 3 E 2 E 1 t t ou in ou M ht ig f ac c in M ht ig f ac c 29 Mike Shor

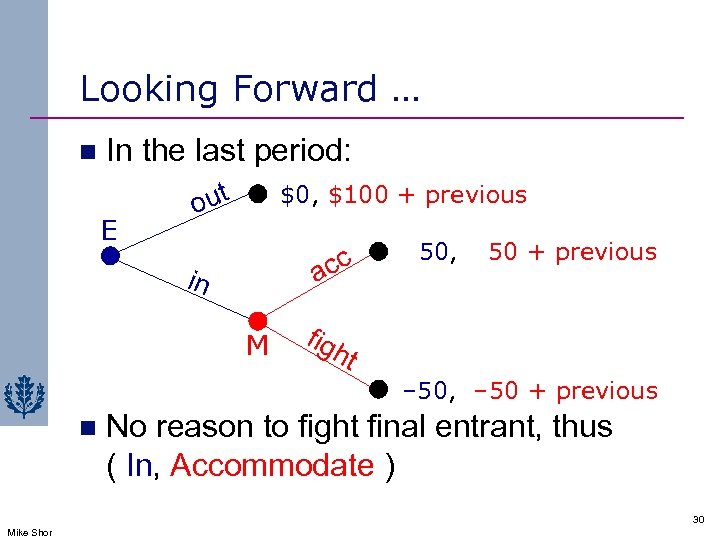Looking Forward … n In the last period: E out $0, $100 + previous c ac in M 50, 50 + previous fig ht – 50, – 50 + previous n No reason to fight final entrant, thus ( In, Accommodate ) 30 Mike Shor

… And Reasoning Back n The Incumbent will not fight the last entrant But then, no reason to fight the previous entrant q … q But then, no reason to fight the first entrant q n Only one sequential equilibrium All entrants play In q Incumbent plays Accommodate q n n But for long games, this is mostly theoretical People “see” the end two to three periods out! 31 Mike Shor

Breakfast Cereals A small sampling of the Kellogg’s portfolio 32 Mike Shor

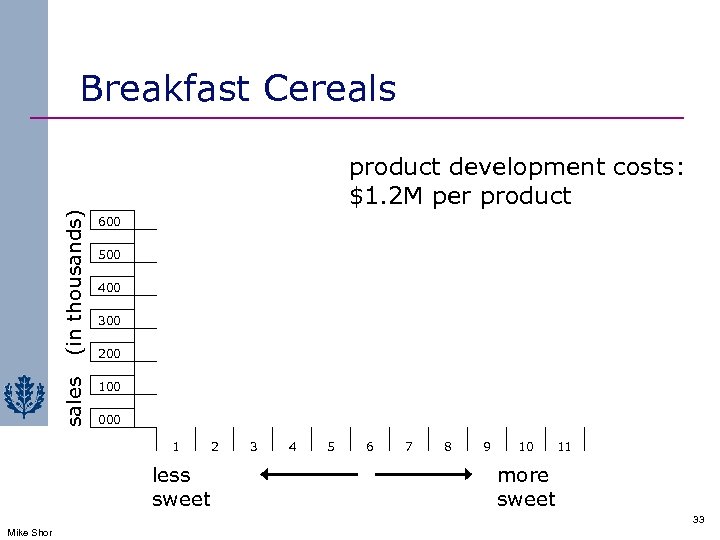Breakfast Cereals (in thousands) 600 sales product development costs: $1. 2 M per product 100 500 400 300 200 000 1 less sweet 2 3 4 5 6 7 8 9 10 11 more sweet 33 Mike Shor

Breakfast Cereals 34 Mike Shor

(in thousands) 600 sales Breakfast Cereals 100 500 400 300 200 000 1 less sweet 2 3 4 5 6 7 8 9 10 11 more sweet 35 Mike Shor

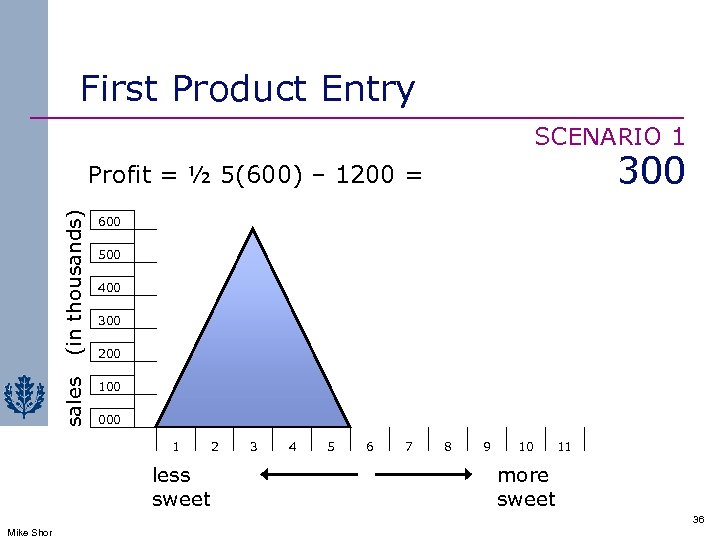First Product Entry SCENARIO 1 300 (in thousands) 600 sales Profit = ½ 5(600) – 1200 = 100 500 400 300 200 000 1 less sweet 2 3 4 5 6 7 8 9 10 11 more sweet 36 Mike Shor

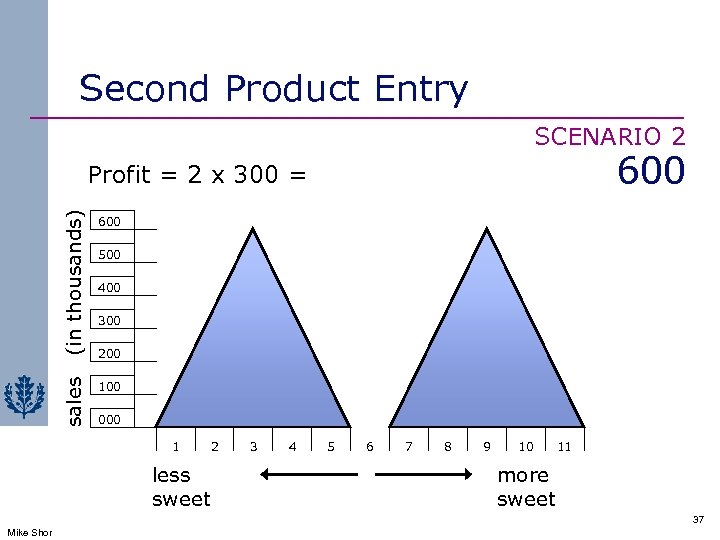Second Product Entry SCENARIO 2 600 (in thousands) 600 sales Profit = 2 x 300 = 100 500 400 300 200 000 1 less sweet 2 3 4 5 6 7 8 9 10 11 more sweet 37 Mike Shor

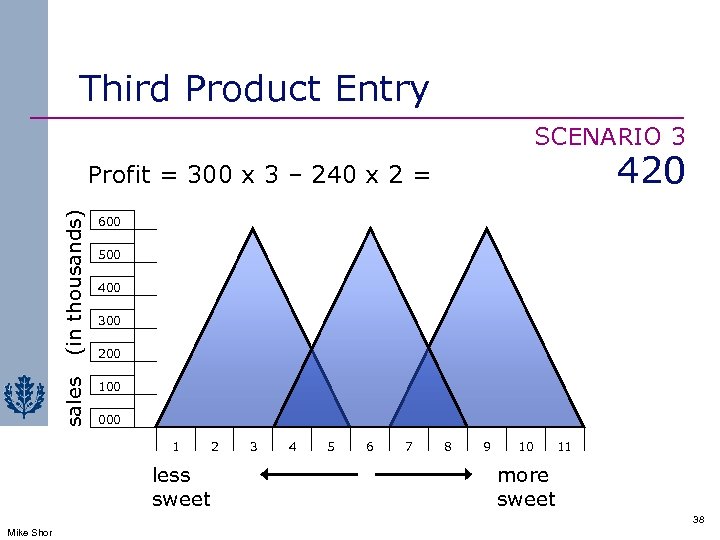Third Product Entry SCENARIO 3 420 (in thousands) 600 sales Profit = 300 x 3 – 240 x 2 = 100 500 400 300 200 000 1 less sweet 2 3 4 5 6 7 8 9 10 11 more sweet 38 Mike Shor

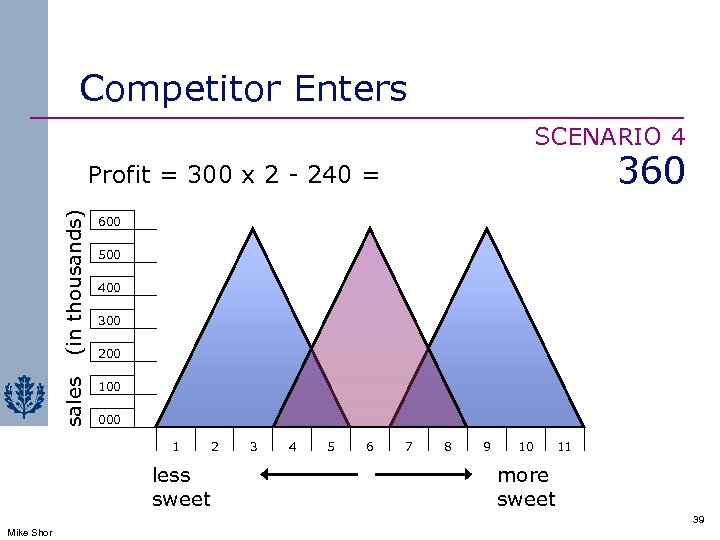Competitor Enters SCENARIO 4 360 (in thousands) 600 sales Profit = 300 x 2 - 240 = 100 500 400 300 200 000 1 less sweet 2 3 4 5 6 7 8 9 10 11 more sweet 39 Mike Shor

Strategic Voting n We saw that voting strategically rather than honestly can change outcomes n Other examples? q Amendments to make bad bills worse q Crossing over in open primaries q “Centrist” voting in primaries 40 Mike Shor

Strategic Voting Maybe majority rule causes this. n Can we eliminate “strategic voting” with other rules? n q Ranking of all candidates q Proportional representation q Run offs q Etc. 41 Mike Shor

Arrow’s Impossibility Theorem n Consider a voting rule that satisfies: q If everyone prefers A to B, B can’t win q If A beats B and C in a three-way race, then A beats B in a two way race n The only political procedure that always guarantees the above is a dictator q No voting system avoids strategic voting 42 Mike Shor

Summary n Thinking forward misses opportunities n Make sure to see the game through to the logical end n Don’t expect others to see the end until it is close q The rule of three steps 43 Mike Shor