Game Theory II l Mixed Strategies l Repeated

Game Theory II l. Mixed Strategies l. Repeated Games l. Co-operative Game Theory

Last time l Games of strategy l l l Sequential games Simultaneous games Dominated strategies Nash equilibria Prisoners’ dilemma Ensuring co-operation; Credible Threat SEEM 3530 Game Theory II 2

Game Theory - History 1838 Cournot “Mathematical Principles of the Theory of Wealth” 1944 von Neumann and Morgenstern “Theory of Games and Economic Behaviour” 1994 Harsanyi, Nash, Selten (Nobel Prize) “for their pioneering analysis of equilibria in theory of non-cooperative games" 2005 Aumann, Schelling "for … understanding of conflict and cooperation through game-theory analysis" SEEM 3530 Game Theory II 3

l Game: l l l description (strategic form) Strategy l l l What does it mean? Does it exist ? Co-operative n-player games l l SEEM 3530 dominant, pure, mixed Equilibrium l l Multiple Players Different/Conflicting goals payoff to each player depends on strategies chosen by all players coalitions reward allocation Game Theory II 4

Nash Equilibrium In an n-player game, a set of strategies (s 1*, s 2*, . . . , sn*) constitute a Nash equilibrium if for each player i, si* is the best response strategy to the strategies s 1*, s 2*, . . . , s*i-1, s*i + 1. . . , sn* for the n-1 other players. SEEM 3530 Game Theory II 5

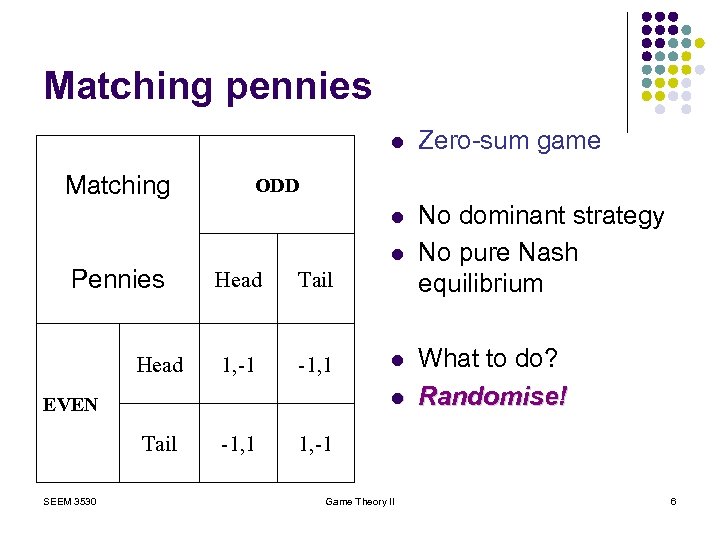Matching pennies l l Matching Pennies Head No dominant strategy No pure Nash equilibrium ODD l Head Tail 1, -1 -1, 1 l l EVEN Tail SEEM 3530 Zero-sum game -1, 1 What to do? Randomise! 1, -1 Game Theory II 6

To mix your plays In American Football, the offense may choose between passing or running for each snap (begin of play). l In tennis, the server may serve to the opponent’s forehand or backhand. l In football, the goalkeeper has to decide if the penalty kick will be to the left, right, or centre. Put yourself in opponent’s shoes! Anticipate! l SEEM 3530 Game Theory II 7

Longest match at Wimbledon l l l Isner won 6 -4, 3 -6, 6 -7 (7 -9), 7 -6 (7 -3), 70 -68 in 11 hours, 5 minutes over 3 days. SEEM 3530 Game Theory II John Isner vs. Nicolas Mahut (23 June, 2010) After 10 hours’ play over 2 days, the score was tied 6 -4, 3 -6, 67(7), 7 -6(3), 59 -59 !! If strategy is predictable, opponent knows how to respond! 8

Unpredictability l l To win requires the mixing of plays in an unpredictable (probabilistic) manner. Unpredictability is a critical element of strategy whenever one player prefer a co-incidence of action and the opponent wishes to avoid it. l l IRD wants to audit those who evade taxes, and those who cheat wants to avoid it. Unpredictable does not necessarily mean all strategies are equally likely. SEEM 3530 Game Theory II 9

Randomized strategies Suppose the strategy-set for player i consists of k strategies, i. e. Si = {Si 1, Si 2, . . . , Sik}, then a mixed strategy for player i is a probability distribution Pi = (Pi 1, Pi 2, . . . , Pik), where 0 < Pik < 1 and ∑ Pik = 1. Pik = probability that player i will play her kth strategy SEEM 3530 Game Theory II 10

Nash’s theorem (1950) In an n-player game where each player has a finite set of strategies, then there always exists at least one Nash equilibrium, possibly involving mixed strategies. What is a pair of Nash-equilibrium mixed strategies for the matching pennies game? SEEM 3530 Game Theory II 11

Matching pennies – mixed-strategy equilibrium l Matching ODD l l Pennies Head Tail Randomise! Each player plays H or T with probability 0. 5. Expected payoff for each player is zero. Why prob = 0. 5? Head 1, -1 -1, 1 l EVEN Tail -1, 1 1, -1 l l SEEM 3530 Suppose ODD plays H with prob. 0. 75. Then EVEN should play H (with EV=0. 75+0. 25(-1) = 0. 5) rather than T (with EV=-0. 5). In response, ODD should play T, not a mixed strategy! Game Theory II 12

Tennis anyone? l l l A mixed strategy does not mean all strategies Probability Server’s Aim to equally likely. receiver A tennis player may have stronger forehand successfully than backhand; Forehand Backhand return serve Server has to choose which side to serve to. Receiver wants to Forehand 90% 20% maximize successful Receiver return percentage; Moves to Server wants to Backhand 30% 60% minimize it. SEEM 3530 Game Theory II 13

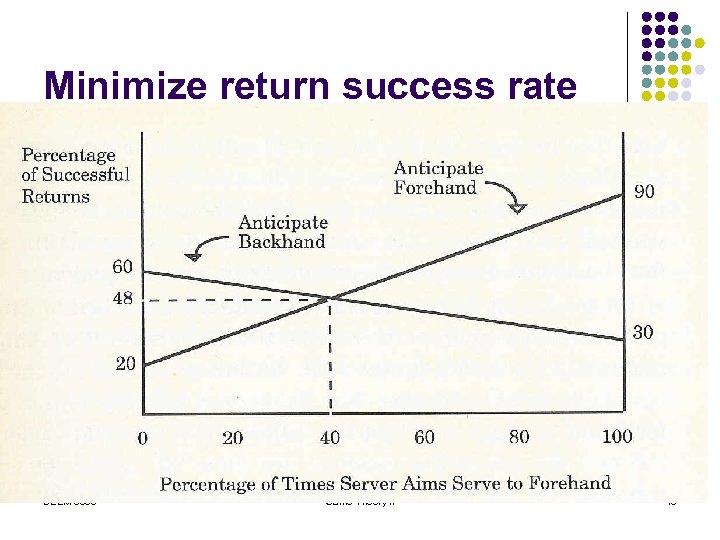
Best return of serve l l l Suppose the server tosses a coin before serving: heads => serve to forehand, tails => backhand. If the receiver always moves to forehand, he is right half of the time. His overall successful return rate is ½ x 90% + ½ x 20% = 55%. If receiver moves to backhand all the time, the overall successful return rate is ½ x 60% + ½ x 30% = 45%. SEEM 3530 Game Theory II 14

Best Serve ? l What is the best strategy for the server? l l l Serve always to forehand [Receiver moves to forehand] : return success rate = 90% Serve always to backhand [ Receiver moves to backhand] : return success rate = 60% Mixed 50: 50 strategy : return success rate = 55 % Mixed strategy is better than the two pure strategies? What is the right “mix” for the server? SEEM 3530 Game Theory II 15

Minimize return success rate SEEM 3530 Game Theory II 16

Best Server Strategy l l l The server needs to find the best probabilities of forehand backhand serving so that the receiver is indifferent between either moves he makes. Consider a serve strategy where Prob(forehand) = 0. 40 Lower than this, receiver will anticipate backhand increase return success. Higher than this, receiver will anticipate forehand increase return success. With the 40: 60 serve strategy, receiver is indifferent between moving to forehand or backhand, and successful return rate is 48%. SEEM 3530 Game Theory II 17

Analysis for the Receiver SEEM 3530 Game Theory II 18

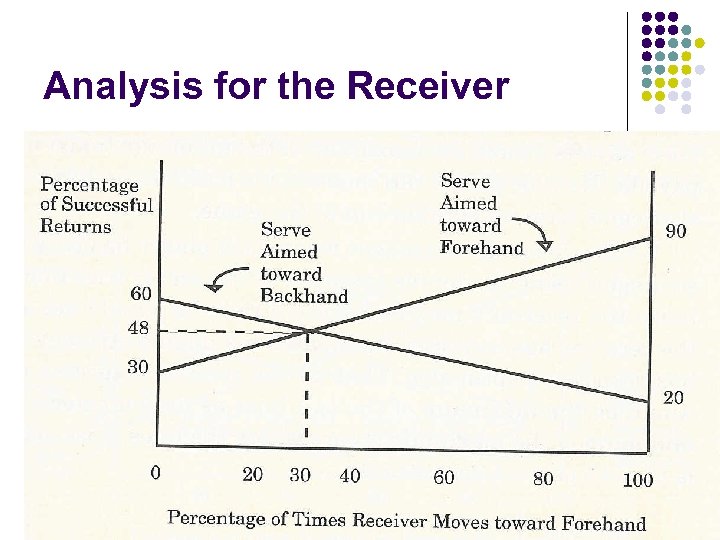
Best Strategy for the Receiver l l Consider a receiver strategy where Prob(move to forehand) = 0. 30 Lower than this, server will aim to forehand return success rate is lower. Higher than this, server will aim to backhand return success rate is lower. With the 30: 70 return strategy, server is indifferent between serving to forehand or backhand, and successful return rate is 48%. SEEM 3530 Game Theory II 19

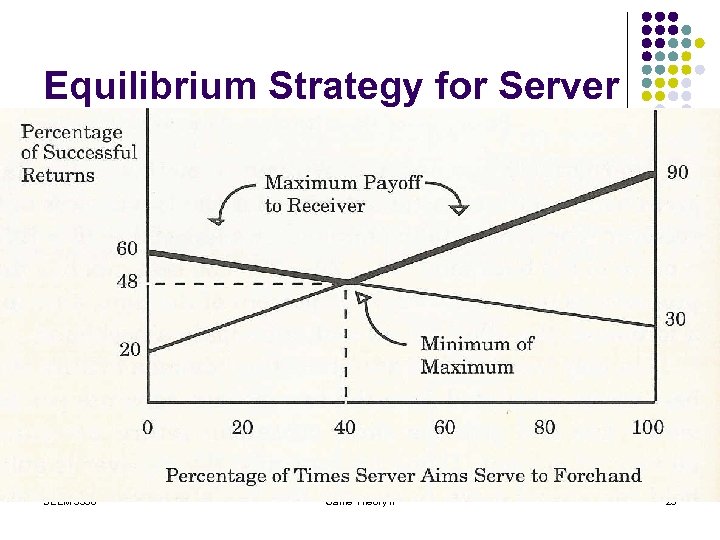
Equilibrium strategies l l Receiver’s best mixed strategy => keeps min return success rate up to 48% Server’s best mixed strategy => keeps max return success rate down to 48% Using his best mix, the receiver is able to hold the server down to exactly the same success percentage as the server is able to achieve using his own best mix. This is a general property of all games with two players whose interests are strictly opposed to each other. SEEM 3530 Game Theory II 20

Mini. Max Theorem (von Neumann, 1928). l l l SEEM 3530 In a two-player zero-sum game (where the gain to one player is the loss of the other), one player tries to minimize the opponents maximum payoff while the other player maximizes its own minimum payoff. The theorem states that the minimum of the maximum (mini-max) payoffs equals to the maximum of the minimum (maxi-min) payoffs. Neither player can improve his position, so these strategies form an equilibrium of the game. Game Theory II 21

Minimax theorem for tennis example l The server should assume that the receiver will correctly anticipate his mixed strategy and act optimally. l l Thus, return success rate will be max of the two receiver strategies. l l l The server tries to minimize the receiver’s maximum payoff. SEEM 3530 The receiver should assume that the server will correctly anticipate his mixed strategy and act optimally. Game Theory II Thus, return success rate will be min of the two server strategies. The receiver tries to maximize his minimum payoff. 22

Equilibrium Strategy for Server SEEM 3530 Game Theory II 23

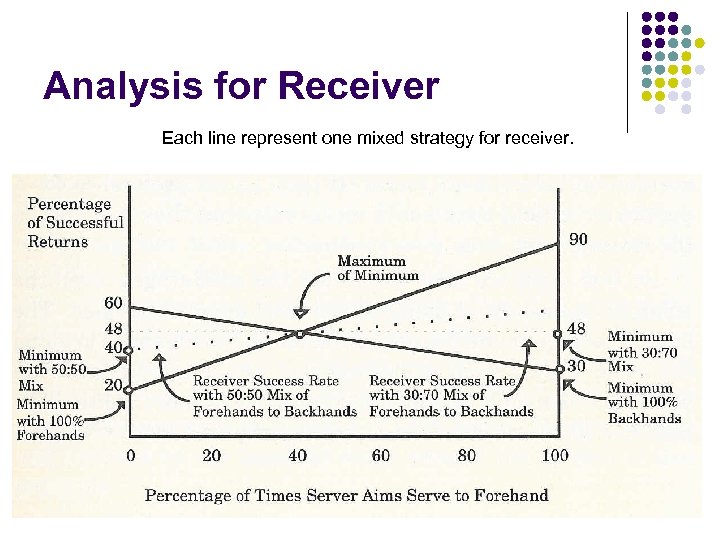Analysis for Receiver Each line represent one mixed strategy for receiver. SEEM 3530 Game Theory II 24

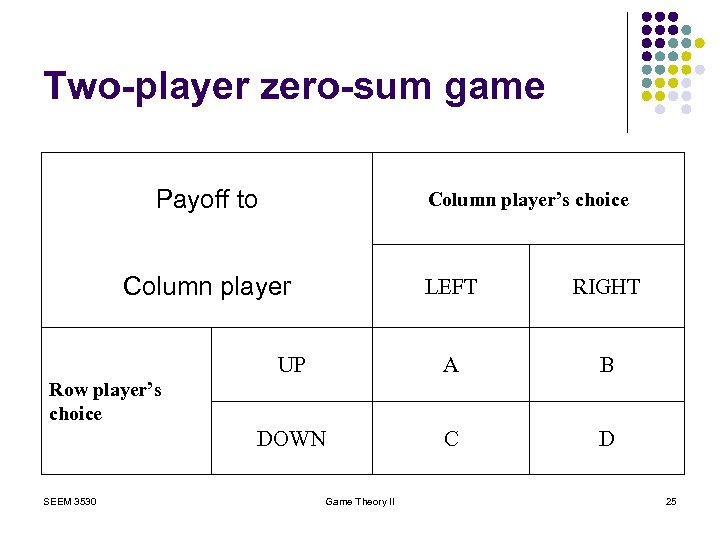Two-player zero-sum game Payoff to Column player’s choice Column player LEFT RIGHT UP A B DOWN C D Row player’s choice SEEM 3530 Game Theory II 25

Minimax strategies l Choose for the column player the best probabilities of LEFT (p) and RIGHT (1−p) so that the row player is indifferent between UP or DOWN. p. A + (1 – p)B = p. C + (1 – p)D p / (1 – p) = (D – B) / (A – C). l Choose the best probabilities for the strategies UP (q) and DOWN (1 -q) for the row player so that the column player is indifferent between his strategies. q. A + (1 – q)C = q. B + (1 – q)D q / (1 – q) = (D – C) / (A – B) l Value of game = (AD – CB)/[(A+D) – (B+C)] SEEM 3530 Game Theory II 26

Computing mixed-strategy equilibria l l l Select mixed strategies so opponent is indifferent about their strategy choices. More general algorithms (e. g. Linear programming) have been used to solve for the equilibria for more complicated zerosum games. Mathematical theoretical links: l l SEEM 3530 Linear algebra duality Minimax results in combinatorics / graph theory Game Theory II 27

Mixed-strategy equilibria The randomized strategy prevents others from exploiting any systematic behaviour of yours! Important: l Randomisation (unpredictability) l l l Use the right randomisation probabilities l l If server follows a pattern (e. g. 4 to forehand, then 6 to backhand), then receiver can exploit this! Using your best mix keep the other player using theirs! Nash “Best response” equilibrium SEEM 3530 Game Theory II 28

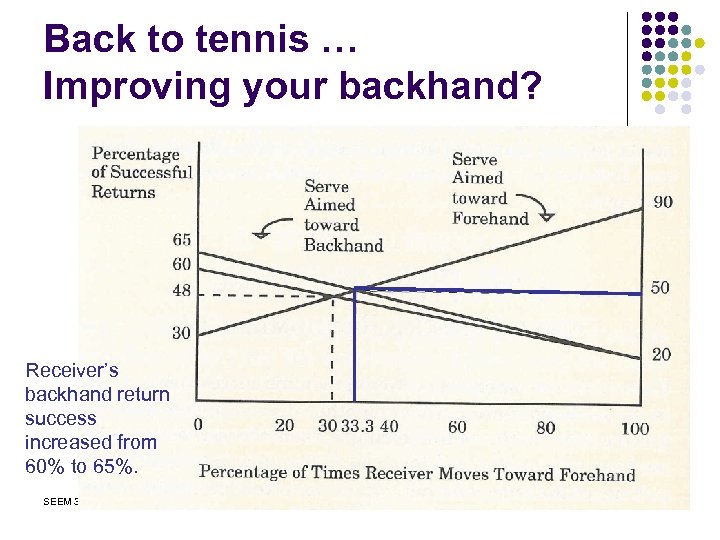Back to tennis … Improving your backhand? Receiver’s backhand return success increased from 60% to 65%. SEEM 3530 Game Theory II 29

Sensitivity Analysis of Equilibrium l l l SEEM 3530 Backhand return success is improved from 60% to 65%. The overall successful return rate goes up from 48% to 50%. The receiver moves more to the forehand: from 30% to 33. 3%. An improved backhand means the receiver uses his backhand return less often than before!? Because … when receiver’s backhand improves, the server serves more to the forehand, so receiver moves more to forehand. A better backhand unlocks the power of your forehand! Game Theory II 30

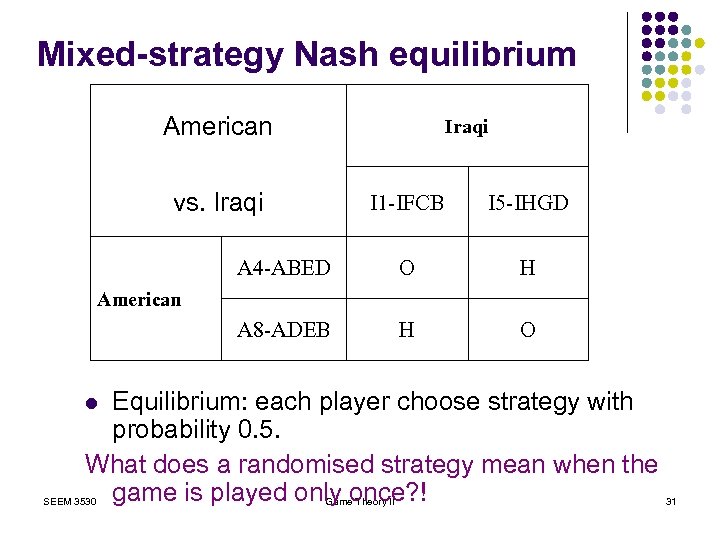Mixed-strategy Nash equilibrium American Iraqi vs. Iraqi I 1 -IFCB I 5 -IHGD A 4 -ABED O H A 8 -ADEB H O American Equilibrium: each player choose strategy with probability 0. 5. What does a randomised strategy mean when the game is played only once? ! l SEEM 3530 Game Theory II 31

Equilibria for Non-Zero-sum Games l l l Suppose players share common interests. A mixed-strategy equilibrium exists, but the randomised strategies may lead to a worse outcome for all players! In O. Henry’s story “The Gift of the Magi”, Della and Jim are a poor couple who truly love each other. Both want to give a Christmas gift for each other. [Since it is a surprise gift, they have not communicated. ] l Della would sell her hair to get Jim a chain for his heirloom watch. l Jim would sell the watch to buy a comb for Della’s beautiful hair. SEEM 3530 Game Theory II 32

Non-zero sum Game: Della and Jim Each prefer to give (2) than to receive (1). Payoff to Jim’s Choice [Della, Jim] Sell Watch Keep Hair 1, 2 0, 0 Sell Hair 0, 0 2, 1 Della’s Choice SEEM 3530 Game Theory II 33

Multiple Nash Equilibria l Two pure Nash equilibria: l l l (Della keeps hair, Jim sells watch); payoff [1, 2] (Della sells hair, Jim keeps watch); payoff [2, 1] A mixed equilibrium: l l l SEEM 3530 Both choose to give with probability 2/3 and choose to receive with probability 1/3. If Jim sells his watch, 1/3 chance that Della has kept her hair. The expected payoff for Jim is 2/3. If Jim keeps his watch, 2/3 chance that Della has sold her hair. The expected payoff for Jim is 2/3. Similar calculations for Della. Expected payoff for each player is 2/3. Game Theory II 34

Lack of co-ordination l l With the mixed strategy, 4 times out of 9, the couple finds that each has sold the item for which the other has bought the gift, and 1 out of 9 times, neither gets any gift. Better for Della and Jim to co-ordinate: l Toss one coin to decide who gives and who receives (i. e. choose one of the two pure equilibria) l Average outcome is 1. 5, better than 2/3 !! Of course, now, no more surprise … no more romance? ! l SEEM 3530 Game Theory II 35

Example – Timing Promotions l l l l Companies use price discount coupons to build market share by enticing consumers to switch brands. Coke offer coupons to attract Pepsi customers; Pepsi also want to give coupons to attract Coke customers. If both offer coupons simultaneously, the effects cancel out and both are worse off (loss of revenue). Coordination between two will be good. The two company could (secretly) agree to offer coupons alternately. Collusion illegal? ! SEEM 3530 Game Theory II 36

Tobacco Industry vs. Government l l Cigarette Advertising was banned on TV in many countries. Many big cigarette manufacturers complained that governments had interfered in the commercial sector. But do the companies really want to advertise on TV? Example from Professor Andrew Buck (from Temple University). SEEM 3530 Game Theory II 37

Government’s Big Favor l Manufacturers’ Profit Philip-Morris [Lorillard, P-M] Don’t Advert Don’t Adv 50, 50 20, 60 Advert 60, 20 l l Lorillard SEEM 3530 27, 27 Game Theory II Before the ban, both manufacturers want to advertise to increase their profits, although this leads to a lose-lose situation. No coordination mechanism in place to enable cooperation. The government’s ban provides the coordination mechanism! 38

Summary l l l l l Games of strategy Nash equilibrium Mixed (randomized) strategies Repeated games Two-person zero-sum games Minimax theorem Unpredictability and randomisation Non-zero-sum games Co-ordination SEEM 3530 Game Theory II 39

Co-operative Game Theory l l Some games involve more than two players. Instead of each player acting independently, players could form coalitions and get synergistic benefits. SEEM 3530 Game Theory II Coalition of Liu Biu (劉備) and Sun Quan (孫權) defeated Cao (曹操 ) at Battle of Red Cliff 40 (赤壁之戰), 208 AD.

n-player Games l l N = {1, 2, … , n} is the set of players A subset of players can form a coalition and receive a joint payoff The characteristic function of a game is defined for each subset S of N; it is the amount v(S) that the members of S can be sure of receiving if they form a coalition. Superadditivity: v(A U B) > v(A) + v(B) SEEM 3530 Game Theory II 41

Example – Land Development Game l l Player 1 owns a piece of land values the land at $1, 000. Player 2 is a subdivider who can develop the land increase its worth to $2, 000. Player 3, another subdivider, can develop the land to be worth $3, 000. What is the characteristic function of this game? v({1}) = 1, v({2}) = v({3}) = 0, v({1, 2, 3}) = 3, v({1, 2}) = 2, v({1, 3}) = 3, v({2, 3}) = 0. SEEM 3530 Game Theory II 42

Rewards and Imputations l l The reward vector x = {x 1, x 2, … xn } denotes the payoff for each player. A reward vector is not reasonable unless: l group rationality individual rationality xi > v({i}) for each i. If x satisfies both conditions, it is called an imputation. l l SEEM 3530 Game Theory II 43

Domination and the Core of a Game The imputation y dominates x through a coalition S, y >S x, if and yi > xi for each i in S. That is, 1. the total value v(S) is sufficient for re-distribution according to y to members in S, and 2. each member i in S prefers yi to xi. The core of an n-player game is the set of all undominated imputations. SEEM 3530 Game Theory II 44

Characterising the Core l An imputation x is in the core of an n-player game if and only if for each subset S of N, (*) Example for the land development game: any vector (x 1, x 2, x 3) with x 2 = 0, x 1+x 3 = 3, and 2 < x 1 < 3 is in the core. l The core can contain many different imputations. SEEM 3530 Game Theory II 45

Games with no core l l The Garbage Game Each of 4 property owners has one bag of garbage and must dump it on someone’s property. If b bags of garbage is dumped on the joint property of a coalition S, then the coalition gets v(S)= −b. What is the characteristic function? SEEM 3530 Game Theory II 46

Characteristic function of the Garbage Game l The best that a coalition S can do is to dump all their garbage on the property of owners NOT in S. v({1, 2, 3, 4}) = − 4 , v(S) = − (4 − |S|) if |S| < 4. l Core? SEEM 3530 Game Theory II 47

Core of the Garbage Game Determine the core of the garbage game. Note that x = (x 1, x 2, x 3, x 4) will be an imputation iff x 1 -3 (G 3) x 2 -3 (G 4) x 3 -3 (G 5) x 4 -3 (G 6) x 1+ x 2 + x 3 + x 4 = -4 (G 7) SEEM 3530 Game Theory II 48

The Garbage Game (cont) Considering all three-player coalitions, for x to be in the core, we must have: x 1+ x 2 + x 3 -1 (G 8) x 1+ x 2 + x 4 -1 (G 9) x 1+ x 3 + x 4 -1 (G 10) x 2 + x 3+ x 4 -1 (G 11) SEEM 3530 Game Theory II 49

The Garbage Game – Empty Core We now show that no imputation x = (x 1, x 2, x 3, x 4) can satisfy (G 8) - (G 11). If x is to be in the core of the garbage game, x must satisfy the inequality generated by adding together (G 8) - (G 11): 3(x 1 + x 2 + x 3 + x 4) -4 (G 12) which contradicts (G 7). This means that no imputation x can satisfy (G 8) (G 11) and the core of the garbage game is empty. SEEM 3530 Game Theory II 50

The Garbage Game (cont) To understand why the garbage game has an empty core, consider the imputation x = (-2, -1, 0), which treats players 1 and 2 unfairly. By joining, players 1 and 2 could ensure that the imputation y = (-1. 5, -0. 5, -1) occurred. Thus, y > {1, 2} x. Similarly, any imputation can be dominated by another imputation. We note that for a two-player version of the garbage game, the core consists of the imputation (-1, -1), and for n > 2, the n-player garbage game has an empty core. SEEM 3530 Game Theory II 51

The Drug Game l l Player 1 invented and patented a new drug. He can sell the formula to either Player 2 or Player 3 to manufacture. Inventor and manufacturer(s) will share the profit of $1 million. Characteristic function: v({1}) = v({2}) = v({3}) = v({2, 3}) = 0, v({1, 2}) = v({1, 3}) = v({1, 2, 3}) = $1 million. SEEM 3530 Game Theory II 52

Core of the Drug Game l (x 1 , x 2 , x 3 ) is an imputation of the drug game iff: xi > 0 for i = 1, 2, 3; x 1 + x 2 + x 3 = 1. l . Further, this is in the core only if: x 1 + x 2 > 1 x 1 + x 3 > 1 x 2 + x 3 > 0 x 1 + x 2 + x 3 > 1 l l The only feasible imputation in the core is (1, 0, 0)! The core contains only one imputation, which emphasize the importance of player 1. SEEM 3530 Game Theory II 53

Core imputation and Equitability l l The core imputation of the drug game allocates ALL benefits to the inventor and none to the manufacturer. Is there another (non-core) imputation that might be more equitable? SEEM 3530 Game Theory II 54

Shapley value (1953) Nobel prize, 2012 Axioms: 1. Individual fairness: φi(v) ≥ v({i}) for every i in N, 2. Efficiency: The total gain is distributed: ∑ φi(v) = v(N), 3. Symmetry: If i and j are equivalent in that v(S {i}) = v(S {j}) for every subset S of N which contains neither i nor j, then φi(v) = φj(v). 4. Zero Player (Null player): A player i is null if v(S {i}) = v(S) for all S not containing i. A null player should receive zero: φi(v) = 0. SEEM 3530 Game Theory II 55

Shapley value l “Average” incremental contribution. All possible ways that the coalition can be formed by adding one player at a time. l Not easy to compute! l SEEM 3530 Game Theory II 56

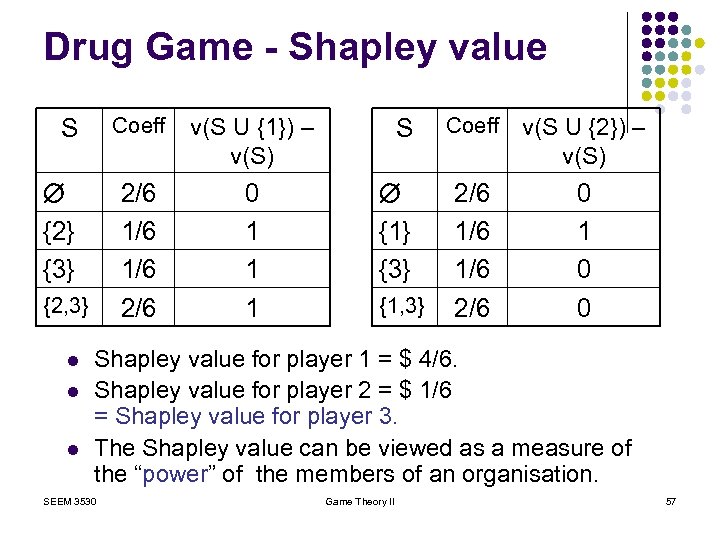Drug Game - Shapley value Coeff {2} {3} {2, 3} l l l v(S U {1}) – v(S) 2/6 1/6 2/6 S 0 1 1 1 S {1} {3} {1, 3} Coeff v(S U {2}) – v(S) 2/6 1/6 2/6 0 1 0 0 Shapley value for player 1 = $ 4/6. Shapley value for player 2 = $ 1/6 = Shapley value for player 3. The Shapley value can be viewed as a measure of the “power” of the members of an organisation. SEEM 3530 Game Theory II 57

Fair and Equal Division Pirates dividing the loot. SEEM 3530 Game Theory II 58

The Judgment of Solomon (1 Kings 3: 16 -28) Pilgrimage church of Frauenberg , Styria (Austria) . Ceiling fresco in the rectory ("emperor's room"). Unknown 17 th century (? ) painter SEEM 3530 Game Theory II 59

Fair Division l Divorce settlements? Dispute resolution? Different players might have different perceptions of value of allocation! l How to divide a cake: l l SEEM 3530 Between 2 ? Among 3 ? Among n ? Game Theory II 60

Envy-free Cake Cutting for 3 (Selfridge and Conway) 1. 2. 3. Alex cuts [into what he thinks are thirds]. Bob trims one piece [to create a 2 -way tie for largest], and sets the trimmings aside. Let Calvin pick a piece, then Bob, then Alex. 1. 4. 5. 6. Require Bob to take a trimmed piece if Calvin does not. Call the person who took the trimmed piece T, and the other (of Bob and Calvin) NT. To deal with the trimmings, let NT cut them [into what he thinks are thirds]. Let players pick pieces in this order: T, Alex, then NT. Su, Francis E. , et al. "Envy-free Cake Division. " Math Fun Facts. http: //www. math. hmc. edu/funfacts/ffiles/30001. 4 -8. shtml SEEM 3530 Game Theory II 61

Co-operative Game theory l l l l SEEM 3530 N-player games coalitions rewards imputations core Shapley value Fair Division Game Theory II 62