Game theory and security Jean-Pierre Hubaux EPFL With

Game theory and security Jean-Pierre Hubaux EPFL With contributions (notably) from M. Felegyhazi, J. Freudiger, H. Manshaei, D. Parkes, and M. Raya

Security Games in Computer Networks • • Security of Physical and MAC Layers Mobile Networks security Anonymity and Privacy Intrusion Detection Systems Sensor Networks Security Mechanisms Game Theory and Cryptography Distributed Systems – More information: http: //lca. epfl. ch/gamesec

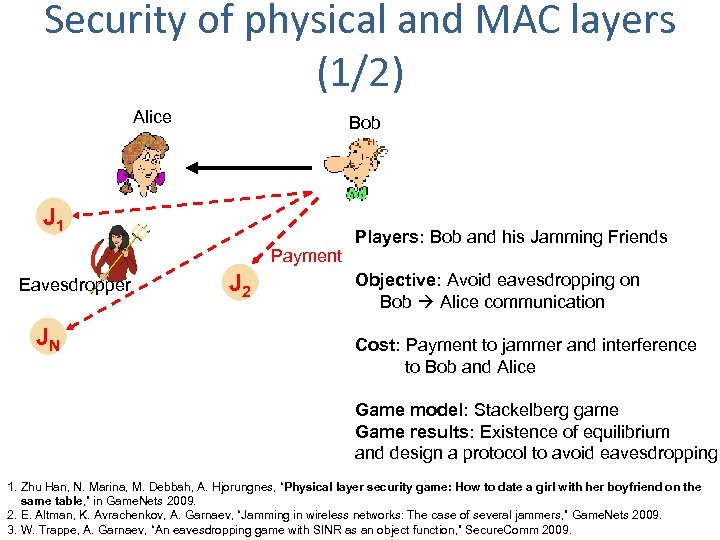
Security of physical and MAC layers (1/2) Alice Bob J 1 Payment Eavesdropper JN J 2 Players: Bob and his Jamming Friends Objective: Avoid eavesdropping on Bob Alice communication Cost: Payment to jammer and interference to Bob and Alice Game model: Stackelberg game Game results: Existence of equilibrium and design a protocol to avoid eavesdropping 1. Zhu Han, N. Marina, M. Debbah, A. Hjorungnes, “Physical layer security game: How to date a girl with her boyfriend on the same table, ” in Game. Nets 2009. 2. E. Altman, K. Avrachenkov, A. Garnaev, “Jamming in wireless networks: The case of several jammers, ” Game. Nets 2009. 3. W. Trappe, A. Garnaev, “An eavesdropping game with SINR as an object function, ” Secure. Comm 2009.

Security of physical and MAC layers (2/2) S W Players (Ad hoc or Infrastructure mode): 1. Well-behaved (W) wireless modes 2. Selfish (S) - higher access probability 3. Malicious (M) - jams other nodes (Do. S) Objective: Find the optimum strategy against M and S nodes M S Reward and Cost: Throughput and Energy W Game model: A power- controlled MAC game solved for Bayesian Nash equilibrium Game results: Introduce Bayesian learning mechanism to update the type belief in repeated games Optimal defense mechanisms against denial of service attacks in wireless networks Y. E. Sagduyu, R. Berry, A. Ephremides, “MAC games for distributed wireless network security with incomplete information of selfish and malicious user types, ” Game. Nets 2009.

Sensor networks security Players: 1. IDS (residing at the base station) 2. Sensor nodes (some nodes could act maliciously: drop packets) IDS at BS Miss Catch Normal Malicious (Fwr Pkts) (Drop Pkts) Sensor Node Least damage False Positive False Negative Best Choice for IDS Game: A repeated game between IDS and nodes to detect the malicious nodes Game Results: Equilibrium calculation in infinite repeated game and using the results to evaluate reputation of nodes A. Agah, M. Asadi, S. K. Das, “Prevention of Do. S Attack in Sensor Networks using Repeated Game Theory, ” ICWN 2006.

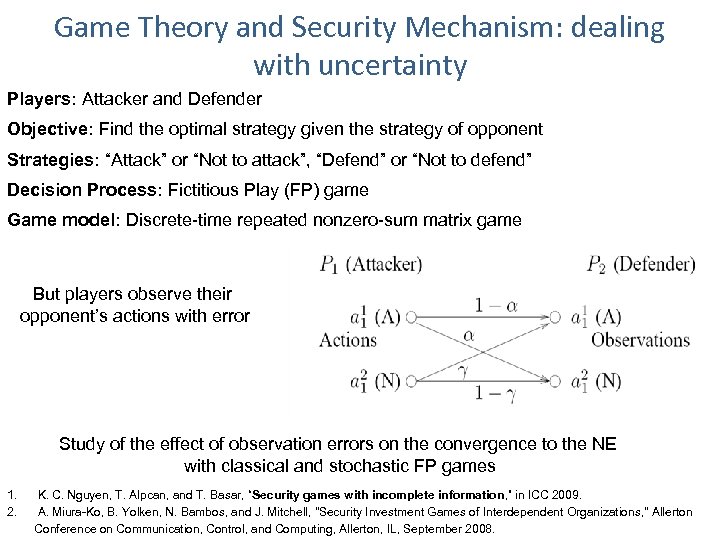
Game Theory and Security Mechanism: dealing with uncertainty Players: Attacker and Defender Objective: Find the optimal strategy given the strategy of opponent Strategies: “Attack” or “Not to attack”, “Defend” or “Not to defend” Decision Process: Fictitious Play (FP) game Game model: Discrete-time repeated nonzero-sum matrix game But players observe their opponent’s actions with error Study of the effect of observation errors on the convergence to the NE with classical and stochastic FP games 1. 2. K. C. Nguyen, T. Alpcan, and T. Basar, “Security games with incomplete information, ” in ICC 2009. A. Miura-Ko, B. Yolken, N. Bambos, and J. Mitchell, "Security Investment Games of Interdependent Organizations, " Allerton Conference on Communication, Control, and Computing, Allerton, IL, September 2008.

Cryptography Vs. Game Theory Issue Cryptography Game Theory Incentive None Payoff Players Totally honest/ malicious Always rational Punishing cheaters Outside the model Central part Solution concept Secure protocol Equilibrium Early stopping Problem Not an issue Y. Dodis, S. Halevi, T. Rubin. A cryptographic Solution to a Game Theoretic Problem. Crypto 2000 7

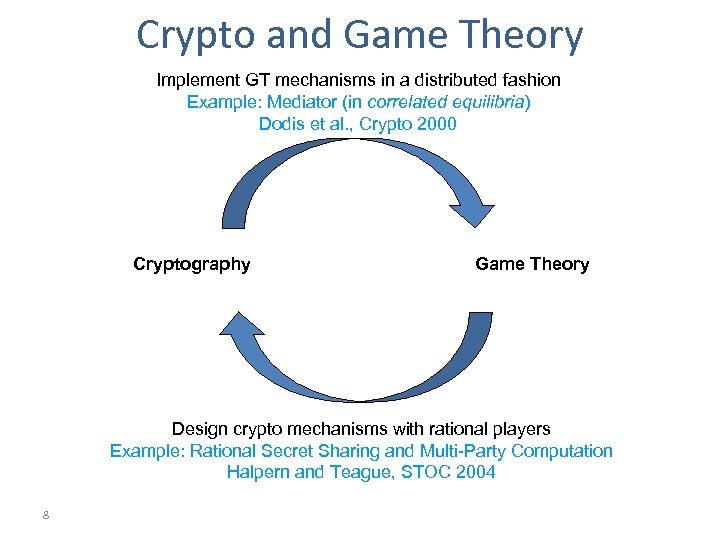
Crypto and Game Theory Implement GT mechanisms in a distributed fashion Example: Mediator (in correlated equilibria) Dodis et al. , Crypto 2000 Cryptography Game Theory Design crypto mechanisms with rational players Example: Rational Secret Sharing and Multi-Party Computation Halpern and Teague, STOC 2004 8

Improving Nash equilibria (1/2) Player 2 Chicken Player 1 Dare Chicken 4, 4 1, 5 Dare 5, 1 0, 0 3 Nash equilibria: (D, C), (C, D), Payoffs: [5, 1] [1, 5] (½ D + ½ C, ½ C+ ½ D) [5/2, 5/2] The payoff [4, 4] cannot be achieved without a binding contract, because it is not an equilibrium Possible improvement 1: communication Toss a fair coin if Head, play (C, D); if Tail, play (D, C) average payoff = [3, 3] Y. Dodis, S. Halevi, and T. Rabin. A Cryptographic solution to a game theoretic problem, Crypto 2000 9

Improving Nash equilibria (2/2) Player 2 Chicken Player 1 Dare Chicken 4, 4 1, 5 Dare 5, 1 0, 0 Possible improvement 2: Mediator Introduce an objective chance mechanism: choose V 1, V 2, or V 3 with probability 1/3 each. Then: - Player 1 is told whether or not V 1 was chosen and nothing else - Player 2 is told whether or not V 3 was chosen and nothing else If informed that V 1 was chosen, Player 1 plays D, otherwise C If informed that V 3 was chosen, Player 2 plays D, otherwise C This is a correlated equilibrium, with payoff [3 1/3, 3 1/3] It assigns probability 1/3 to (C, C), (C, D), and (D, C) and 0 to (D, D) How to replace the mediator by a crypto protocol: see Dodis et al. 10

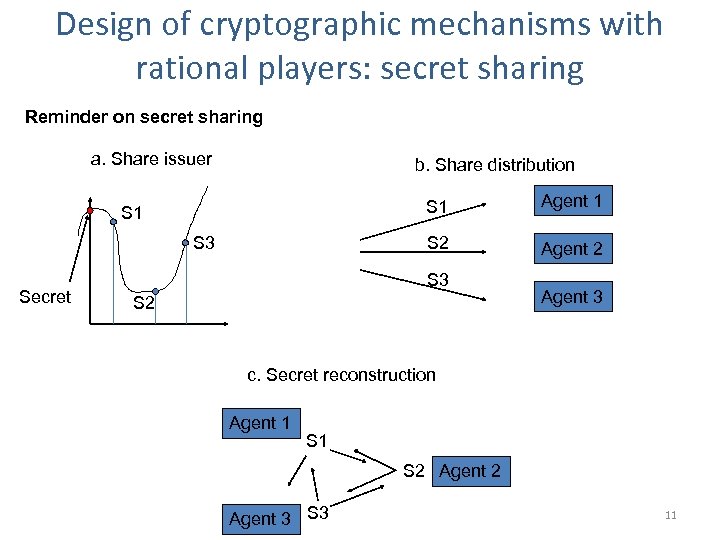
Design of cryptographic mechanisms with rational players: secret sharing Reminder on secret sharing a. Share issuer b. Share distribution S 1 S 3 Secret Agent 1 S 2 S 1 Agent 2 S 3 S 2 Agent 3 c. Secret reconstruction Agent 1 S 2 Agent 3 S 3 11

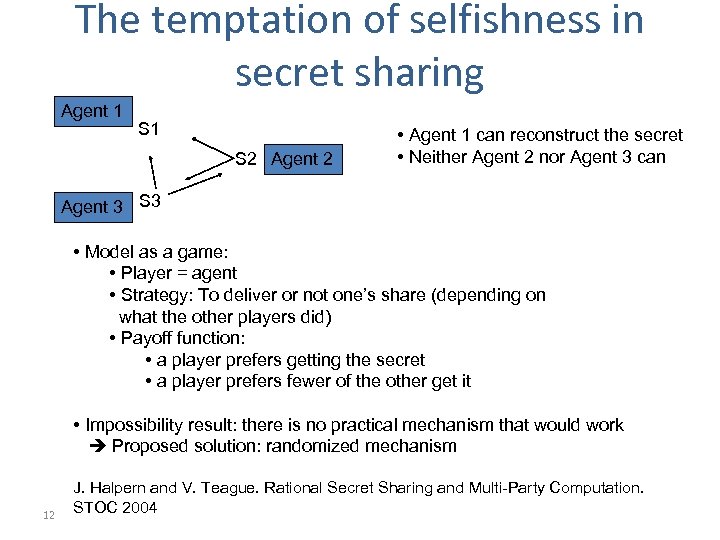
The temptation of selfishness in secret sharing Agent 1 S 2 Agent 2 • Agent 1 can reconstruct the secret • Neither Agent 2 nor Agent 3 can Agent 3 S 3 • Model as a game: • Player = agent • Strategy: To deliver or not one’s share (depending on what the other players did) • Payoff function: • a player prefers getting the secret • a player prefers fewer of the other get it • Impossibility result: there is no practical mechanism that would work Proposed solution: randomized mechanism 12 J. Halpern and V. Teague. Rational Secret Sharing and Multi-Party Computation. STOC 2004

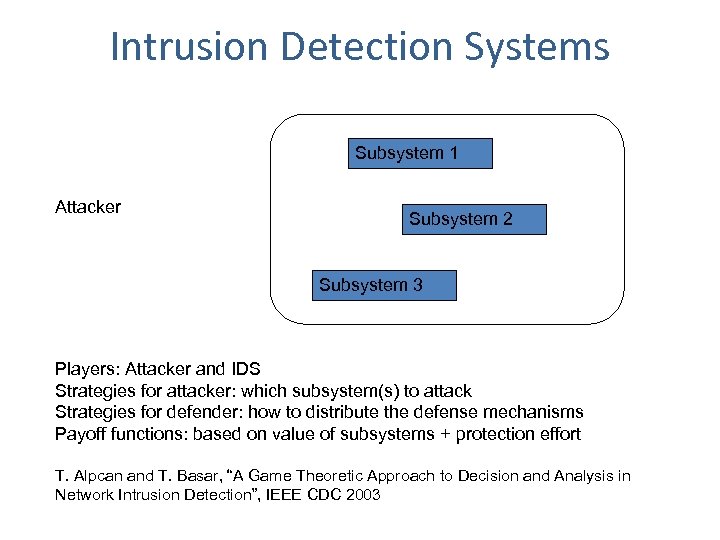
Intrusion Detection Systems Subsystem 1 Attacker Subsystem 2 Subsystem 3 Players: Attacker and IDS Strategies for attacker: which subsystem(s) to attack Strategies for defender: how to distribute the defense mechanisms Payoff functions: based on value of subsystems + protection effort T. Alpcan and T. Basar, “A Game Theoretic Approach to Decision and Analysis in Network Intrusion Detection”, IEEE CDC 2003

Two detailed examples • Revocation Games in Ephemeral Networks [CCS 2008] • On Non-Cooperative Location Privacy: A Game -Theoretic Analysis [CCS 2009] 14

Misbehavior in Ad Hoc Networks Traditional ad hoc networks A M Ephemeral networks B • Packet forwarding • Routing • Large scale • High mobility • Data dissemination Solution to misbehavior: Reputation systems ? 15

Reputation vs. Local Revocation • Reputation systems: – Often coupled with routing/forwarding – Require long-term monitoring – Keep the misbehaving nodes in the system • Local Revocation – Fast and clear-cut reaction to misbehavior – Reported to the credential issuer – Can be repudiated 16

Tools of the Revocation Trade • Wait for: – Credential expiration – Central revocation • Vote with: – Fixed number of votes – Fixed fraction of nodes (e. g. , majority) • Suicide: – Both the accusing and accused nodes are revoked Which tool to use? 17

How much does it cost? • Nodes are selfish • Revocation costs • Attacks cause damage How to avoid the free rider problem? Game theory can help: models situations where the decisions of players affect each other 18

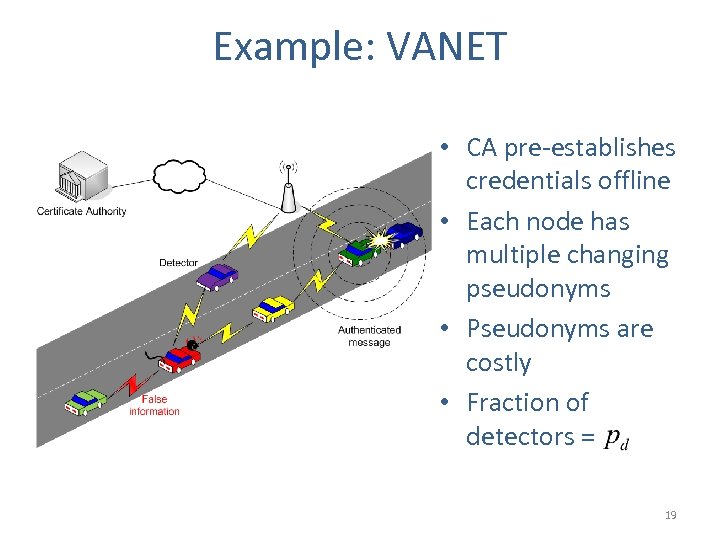
Example: VANET • CA pre-establishes credentials offline • Each node has multiple changing pseudonyms • Pseudonyms are costly • Fraction of detectors = 19

Revocation Game • Key principle: Revoke only costly attackers • Strategies: – Abstain (A) – Vote (V): votes are needed – Self-sacrifice (S) • benign nodes, including • attackers • Dynamic (sequential) game detectors 20

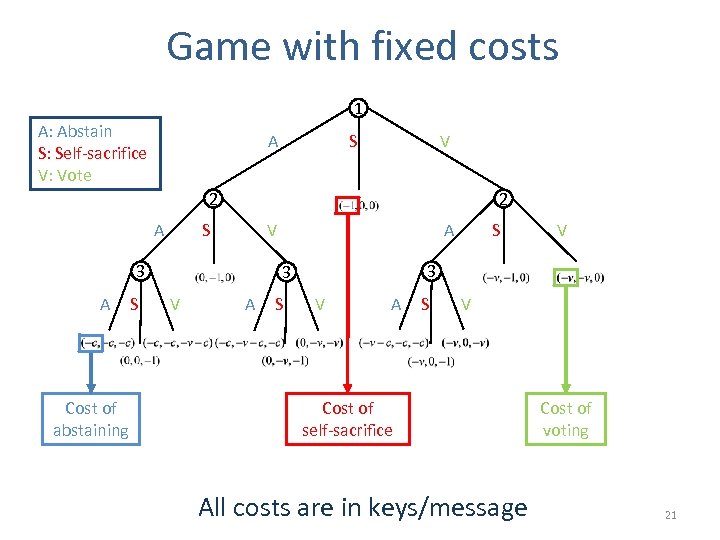
Game with fixed costs 1 A: Abstain S: Self-sacrifice V: Vote A S V 2 A 2 S 3 A Cost of abstaining S A V A S V 3 3 V S V A S V Cost of self-sacrifice All costs are in keys/message Cost of voting 21

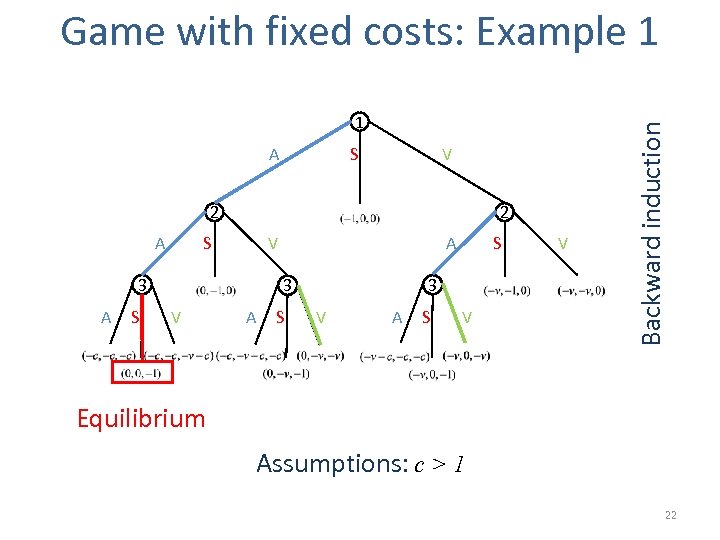
1 A S V 2 A 2 S 3 A S A V 3 3 V A S S V A S V V Backward induction Game with fixed costs: Example 1 Equilibrium Assumptions: c > 1 22

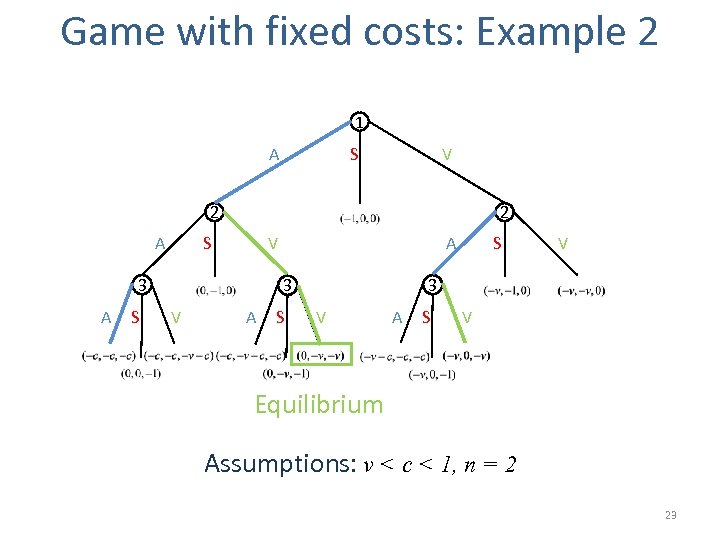
Game with fixed costs: Example 2 1 A S V 2 A 2 S 3 A S A V A S V 3 3 V S V A S V Equilibrium Assumptions: v < c < 1, n = 2 23

Game with fixed costs: Equilibrium Theorem 1: For any given values of ni, nr, v, and c, the strategy of player i that results in a subgame-perfect equilibrium is: ni = Number of remaining nodes that can participate in the game nr = Number of remaining votes that is required to revoke Revocation is left to the end, doesn’t work in practice 24

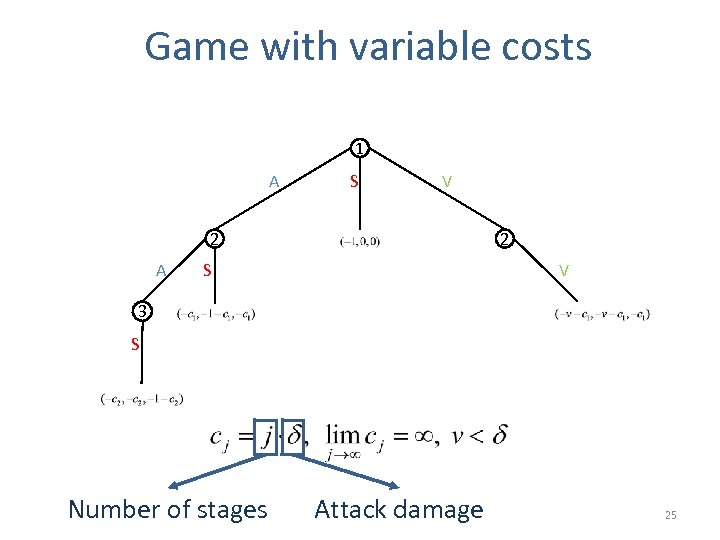
Game with variable costs 1 A S V 2 A 2 V S 3 S Number of stages Attack damage 25

Game with variable costs: Equilibrium Theorem 2: For any given values of ni, nr, v, and δ, the strategy of player i that results in a subgame-perfect equilibrium is: Revocation has to be quick 26

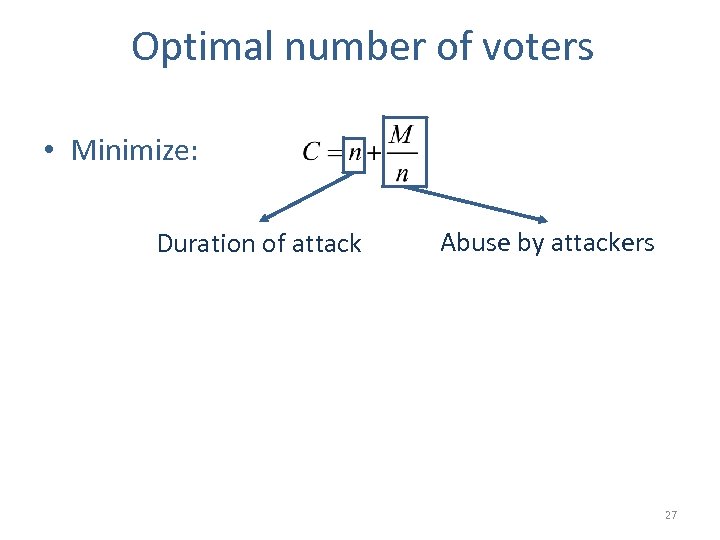
Optimal number of voters • Minimize: Duration of attack Abuse by attackers 27

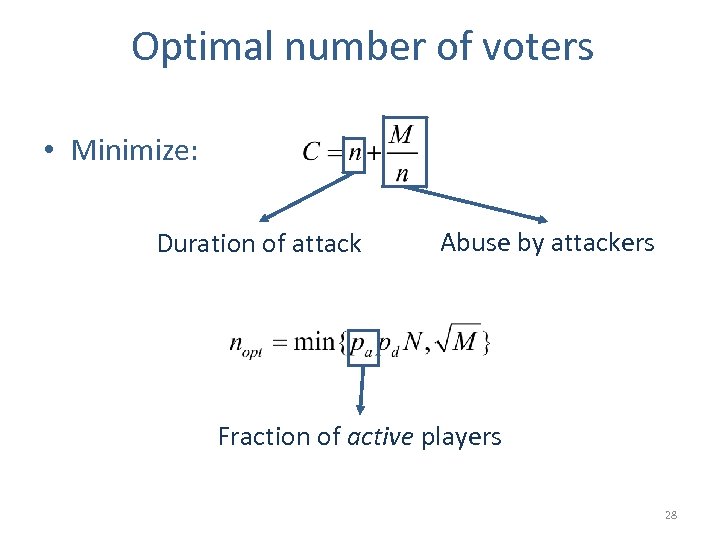
Optimal number of voters • Minimize: Duration of attack Abuse by attackers Fraction of active players 28

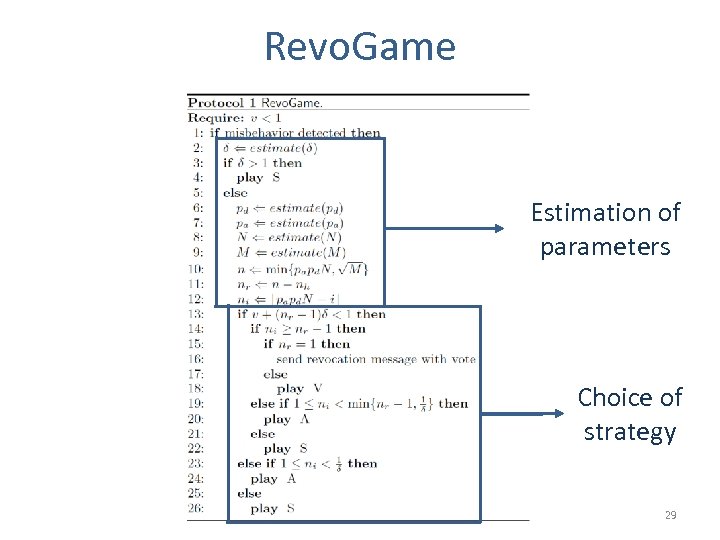
Revo. Game Estimation of parameters Choice of strategy 29

Evaluation • Tra. NS, ns 2, Google Earth, Manhattan • 303 vehicles, average speed = 50 km/h • Fraction of detectors • Damage/stage • Cost of voting • False positives • 50 runs, 95 % confidence intervals 30

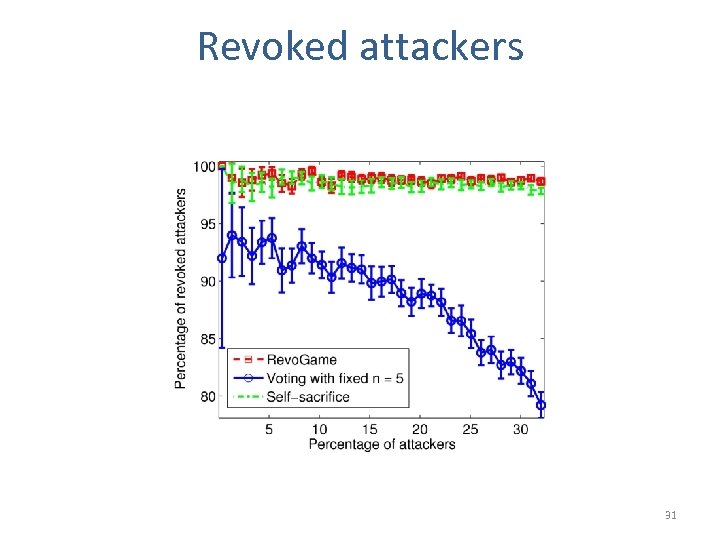
Revoked attackers 31

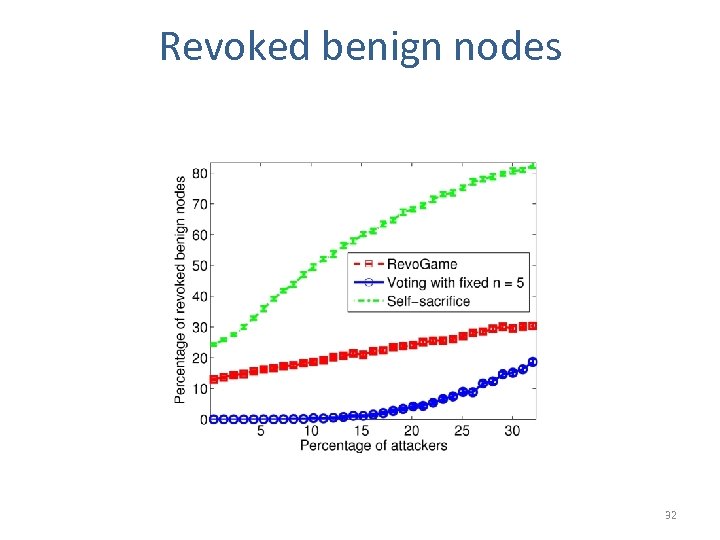
Revoked benign nodes 32

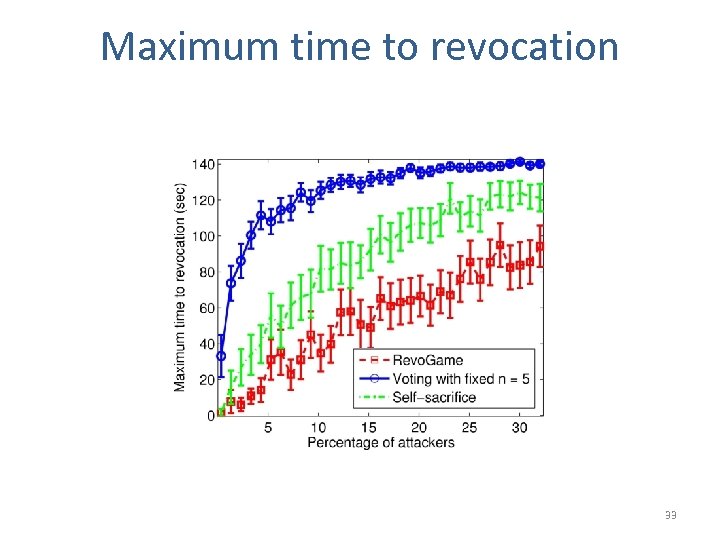
Maximum time to revocation 33

Conclusion • Local revocation is a viable mechanism for handling misbehavior in ephemeral networks • The choice of revocation strategies should depend on their costs • Revo. Game achieves the elusive tradeoff between different strategies 34

Two detailed examples • Revocation Games in Ephemeral Networks [CCS 2008] • On Non-Cooperative Location Privacy: A Game -Theoretic Analysis [CCS 2009] 35

Pervasive Wireless Networks Vehicular networks Mobile Social networks Human sensors Personal Wi. Fi bubble 36

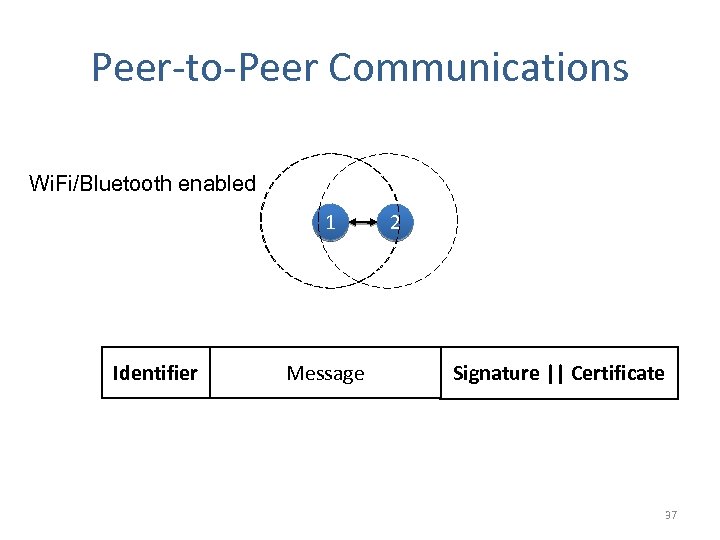
Peer-to-Peer Communications Wi. Fi/Bluetooth enabled 1 Identifier Message 2 Signature || Certificate 37

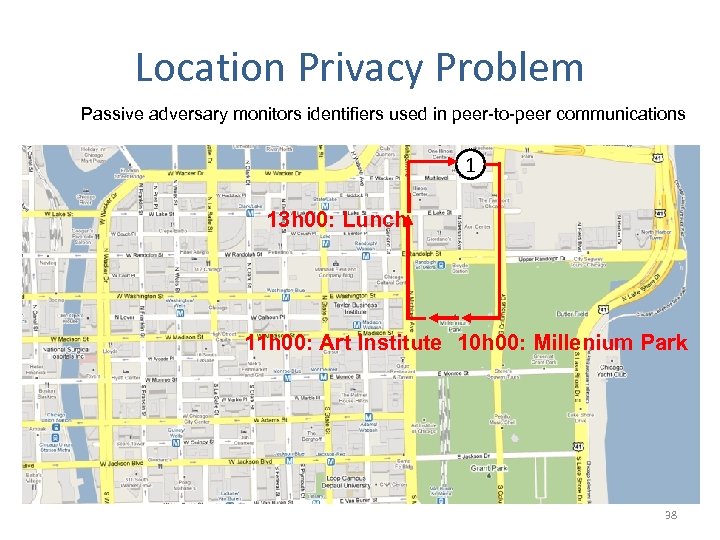
Location Privacy Problem Passive adversary monitors identifiers used in peer-to-peer communications 1 13 h 00: Lunch 11 h 00: Art Institute 10 h 00: Millenium Park 38

Previous Work Pseudonym Identifier Message • Pseudonymity is not enough for location privacy [1, 2] • Removing pseudonyms is not enough either [3] Spatio-Temporal correlation of traces [1] P. Golle and K. Partridge. On the Anonymity of Home/Work Location Pairs. Pervasive Computing, 2009 [2] B. Hoh et al. Enhancing Security & Privacy in Traffic Monitoring Systems. Pervasive Computing, 2006 [3] B. Hoh and M. Gruteser. Protecting location privacy through path confusion. SECURECOMM, 2005 39

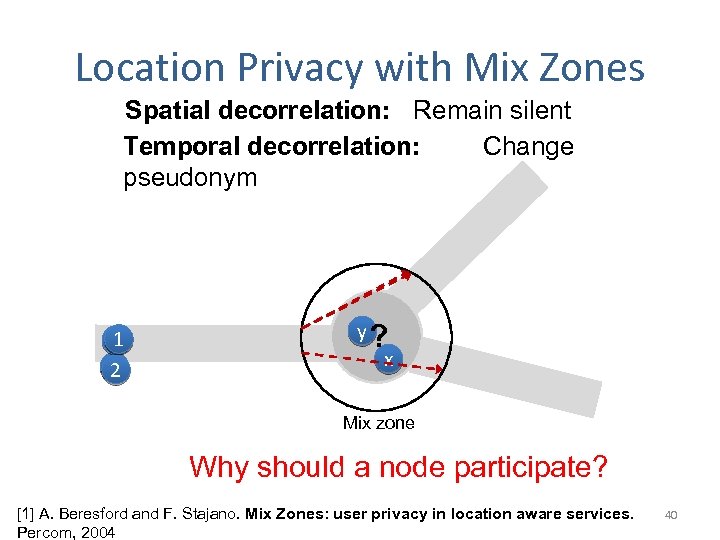
Location Privacy with Mix Zones Spatial decorrelation: Remain silent Temporal decorrelation: Change pseudonym 1 1 2 y? x Mix zone Why should a node participate? [1] A. Beresford and F. Stajano. Mix Zones: user privacy in location aware services. Percom, 2004 40

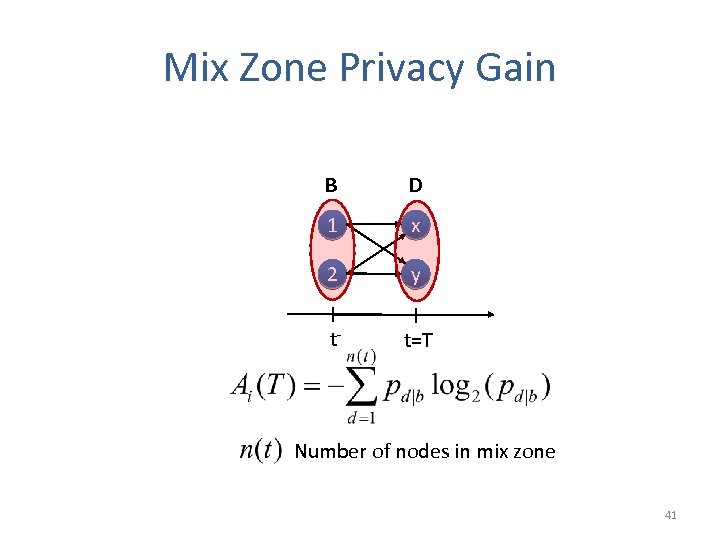
Mix Zone Privacy Gain B D 1 x 2 y t- t=T Number of nodes in mix zone 41

Cost caused by Mix Zones • Turn off transceiver + • Routing is difficult • Need new authenticated pseudonyms + = 42

Problem Tension between cost and benefit of mix zones When should nodes change pseudonym? 43

Method Rational Behavior Selfish optimization Security protocols Multi-party computations • Game theory – Evaluate strategies – Predict evolutionof security/privacy • Example – Cryptography – Revocation – Privacy mechanisms 44

Outline 1. User-centric Model 2. Pseudonym Change Game 3. Results 45

Mix Zone Establishment • In pre-determined regions [1] • Dynamically [2] – Distributed protocol [1] A. Beresford and F. Stajano. Mix Zones: user privacy in location aware services. Percom. W, 2004 [2] M. Li et al. Swing and Swap: User-centric approaches towards maximizing location privacy. WPES, 2006 46

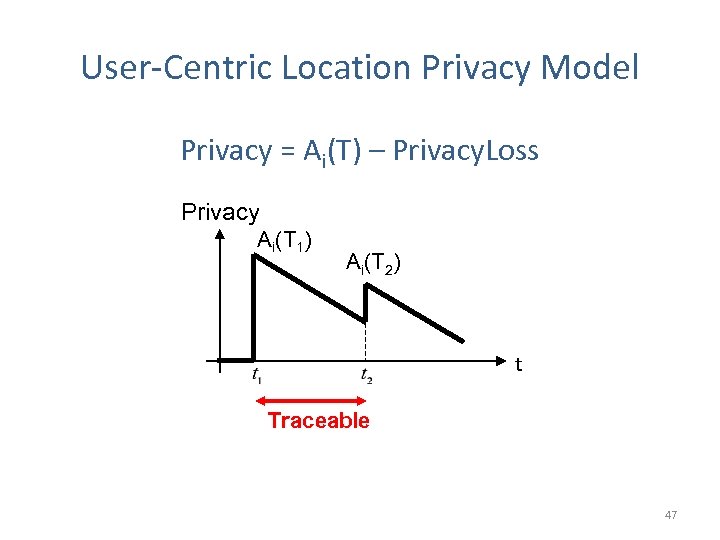
User-Centric Location Privacy Model Privacy = Ai(T) – Privacy. Loss Privacy Ai(T 1) Ai(T 2) t Traceable 47

Pros/Cons of user-centric Model • Pro – Control when/where to protect your privacy • Con – Misaligned incentives 48

Outline 1. User-centric Model 2. Pseudonym Change Game 3. Results 49

Assumptions 1 2 Pseudonym Change game – Simultaneous decision – Players want to maximize their payoff – Consider privacy upperbound Ai(T) = log 2(n(t)) 50

Game Model • Players – Mobile nodes in transmission range – There is a game iif • Strategy – Cooperate (C) : – Defect (D): Change pseudonym Do not change pseudonym 51

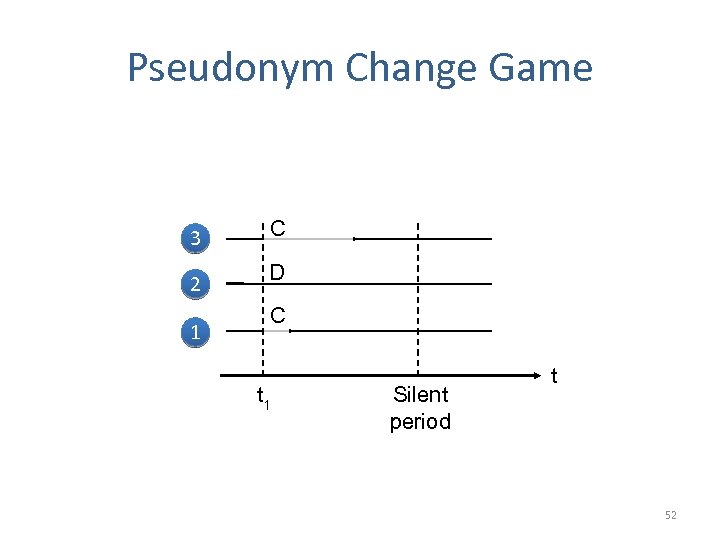
Pseudonym Change Game 3 C 2 D 1 C t 1 Silent period t 52

Payoff Function ui = privacy - cost If C&Not alone, then ui = Ai(T)- γ If C&Alone, then u i = u i -- γ If D, then ui = u i 53

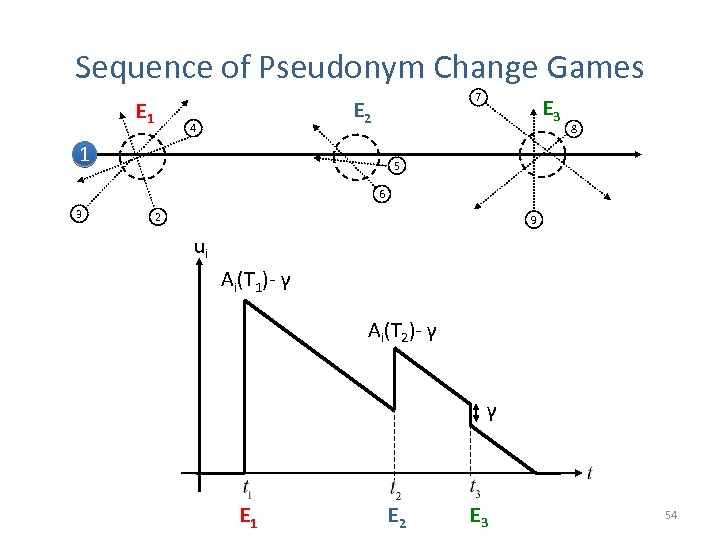
Sequence of Pseudonym Change Games E 1 7 E 2 4 1 E 3 8 5 6 3 2 9 ui Ai(T 1)- γ Ai(T 2)- γ γ E 1 E 2 E 3 54

Outline 1. User-centric Model 2. Pseudonym Change Game 3. Results 55

C-Game Complete information Each player knows the payoff of its opponents 56

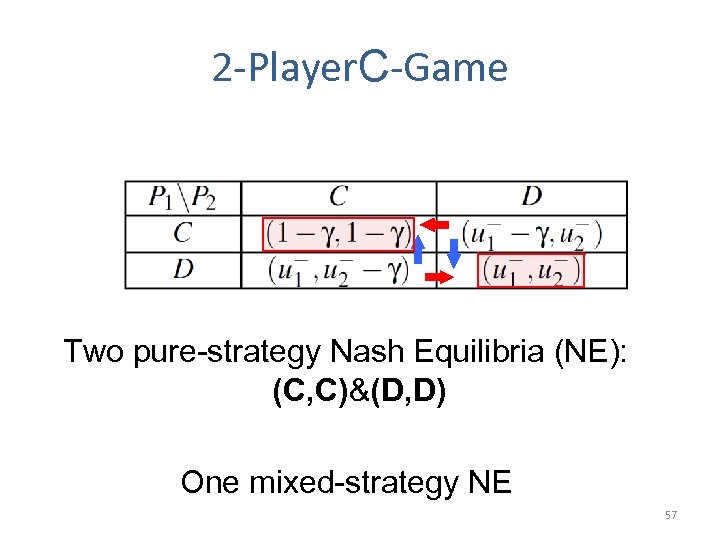
2 -Player. C-Game Two pure-strategy Nash Equilibria (NE): (C, C)&(D, D) One mixed-strategy NE 57

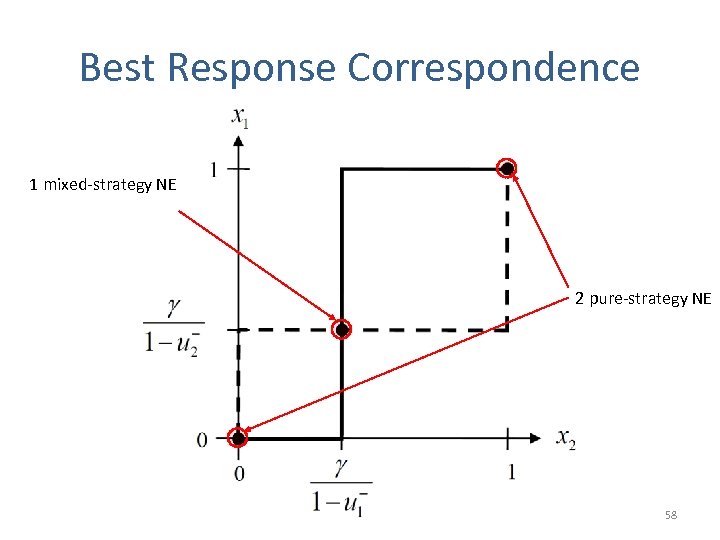
Best Response Correspondence 1 mixed-strategy NE 2 pure-strategy NE 58

n-Player. C-Game Theorem The static n-player pseudonym change. C-game has at least 1 and at most 2 pure strategy Nash equilibria. • All Defection is always a NE • A NE with cooperation exists iif there is a group of k users with in the group of k nodes 59

C-Game Results Result 1: high coordination among nodes at NE • Change pseudonyms only when necessary • Otherwise defect 60

I-Game Incomplete information Players don’t know the payoff of their opponents 61

Bayesian Game Theory Define type of player θi = ui. Predict action of opponents based on pdf over type 62

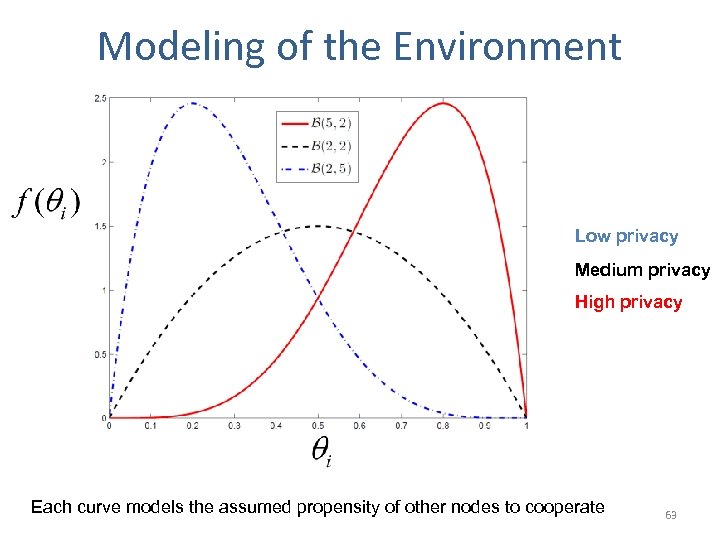
Modeling of the Environment Low privacy Medium privacy High privacy Each curve models the assumed propensity of other nodes to cooperate 63

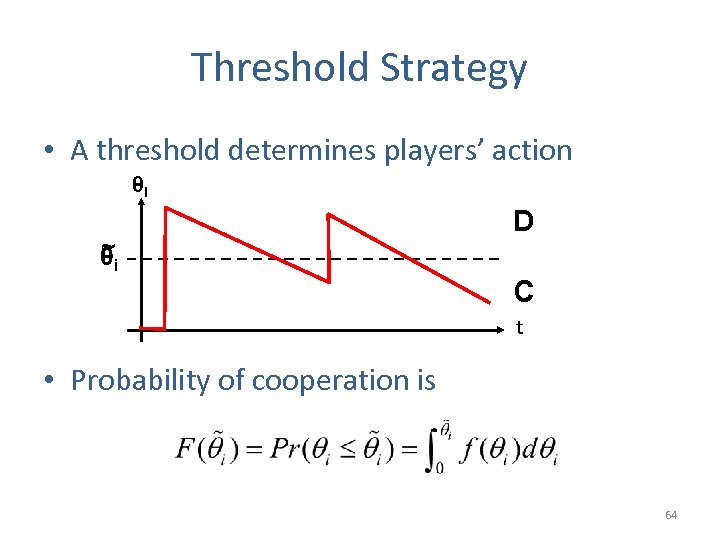
Threshold Strategy • A threshold determines players’ action θi ~ θi D C t • Probability of cooperation is 64

2 -Player I-Game Bayesian NE ~ Find threshold θi* such that Average utility of cooperation = Average utility of defection 65

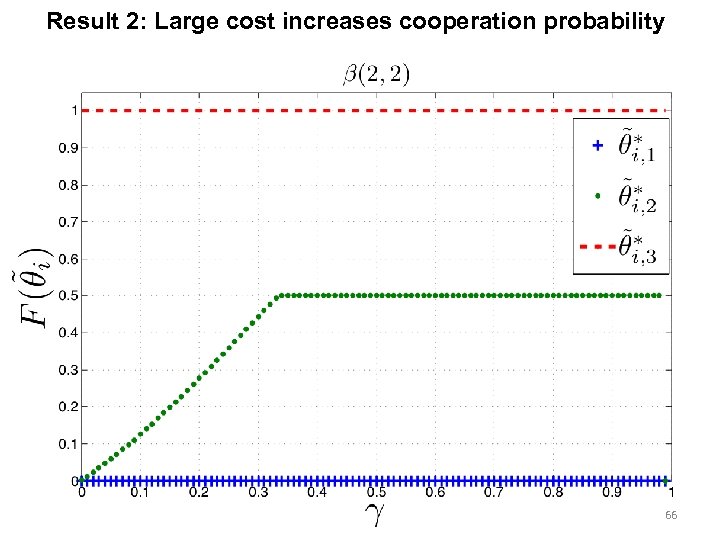
Result 2: Large cost increases cooperation probability 66

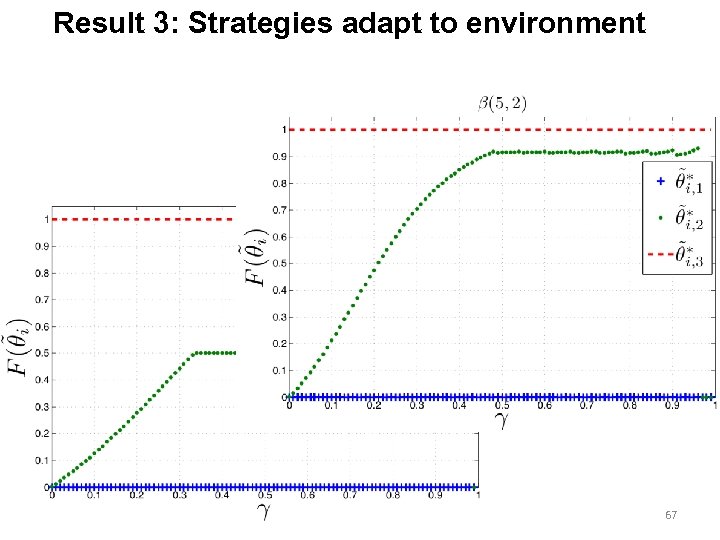
Result 3: Strategies adapt to environment 67

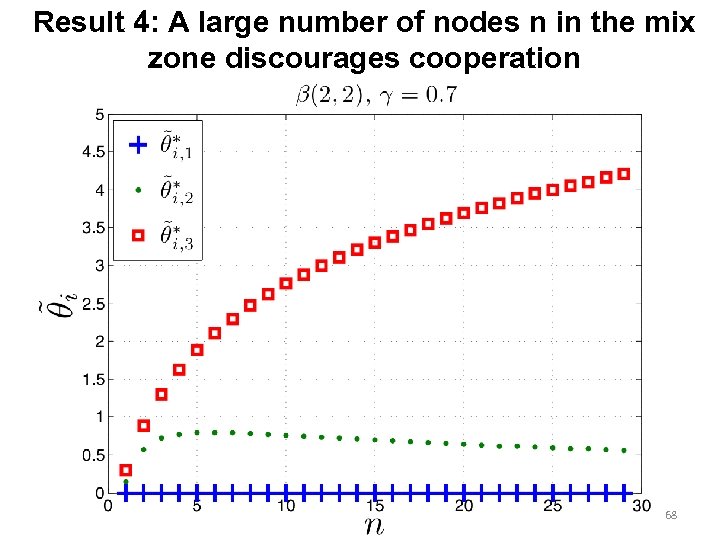
Result 4: A large number of nodes n in the mix zone discourages cooperation 68

Conclusion on non-cooperative location privacy • Considered problem of selfishness in location privacy schemes based on multiple pseudonyms • Results – Non-cooperative behavior reduces the achievable location privacy – If cost is high, users care about coordination – As the number of players increases, selfish nodes tend to not cooperate 69