Futures on Debt Securities Types T-Bills

T-Bill Futures • T-Bill futures call for the delivery or purchase of a T-bill with a maturity of 91 days and a face value of $1 M. Used for speculating on S-T rates and hedging. • Prices on T-Bill futures are quoted in terms of the IMM index or discount yield (Rd): • Formula to Convert:

Eurodollar Futures are similar to T-Bill futures. They call for delivery or purchase of Eurodollar deposits with a maturity of 90 days and F = $1 M. They are quoted in terms of the IMM index. They differ from T-Bill futures in that there is a cash settlement feature. The cash settlement is based on the LIBOR. Used for speculating on ST rates and for hedging bank positions ( correlated with CD rates).

T-Bond Futures • T-Bond Futures contracts call for the delivery or purchase of a T-Bond with a face value of $100, 000. The contract allows for the delivery of a number of T-Bonds; there is a conversion factor used to determine the actual price of the futures given the bond that is delivered. • T-Bond futures are quoted in terms of a T-Bond with an 8% coupon, semiannual payments, maturity of 15 years, and face value of $100.

Long Hedging with Debt Futures • Bond manager expecting an inflow of cash in the future which he plans to invest in T-Bills for 90 days (or long term). To hedge the manager would go long in T-Bill futures (T-Bond Futures).

Short Hedging with Debt Futures Short Hedging Strategies: • Bond manager expecting to liquidate a bond portfolio in the future. • A company planning to issue bonds or borrow. • A bank or financial institution managing its maturity gap. • A company wanting to fix a variable-rate loan.

Speculation • Outright Positions – Long: Expect rates to decrease. ST Rates: use T-Bills or Eurodollar futures; LT: use T-Bonds or Notes. – Short: Expect rates to increase. ST: use T-Bills or Eurodollars; LT: use T-Bonds or Notes. • Spread: – Intracommodity – Intercommodity: • Expect Recession: Short MBI, Long T-Bond or Short Eurodollar, long TBill. • Expect Upward Twist of YC: Short T-B 0 nd, Long T-Bill.

Cross Hedging • Cross Hedging is hedging a position with a futures contract in which the asset underlying the futures is different than the asset to be hedged. • Example: Future CP sale hedged with T-Bill futures; AA Bond portfolio hedged with T-Bond futures. • For bond positions, the following formula can be used:

Futures Pricing and Hedging with Debt Futures Contracts

Pricing T-Bill Futures • Carrying Cost Model:

Pricing T-Bill Futures • Example: • If the rate on a 161 -day spot T-Bill is 5. 7% and the repo rate (or RF rate ) for 70 days is 6. 38%, then the price on a T-Bill futures contract with an expiration of 70 days would be 98. 74875:

Pricing T-Bill Futures • The futures price is governed by arbitrage. If the market price is above f*, arbitrageurs would short the futures and go long in the spot. • Example: Suppose Fm = 99. An arbitrageur would go short in the futures, agreeing to sell a 91 -day T-Bill for 99 seventy days later and would go long in the spot, borrowing 97. 5844 at 6. 38% for 70 days to finance the purchase of the 161 -day T-Bill that is trading at 97. 5844. Seventy days later (expiration), the arbitrageur would sell the bill (which now would have a maturity of 91 days) on the futures for 99 (fm) and pay off his financing debt of 98. 74875 (f*), realizing a cash flow of $2, 513:

Pricing T-Bill Futures • Note at fm = 99, a money market manager planning to invest for 70 days in a T-Bill at 6. 38% could earn a greater return by buying a 161 -day bill and going short in the 70 -day T-Bill futures to lock in the selling price. For example, using the above numbers, if a money market manager were planning to invest 97. 5844 for 70 days, she could buy a 161 -day bill for that amount and go short in the futures at 99. Her return would be 7. 8%, compared to only 6. 38% from the 70 -day T-Bill.

Pricing T-Bill Futures • If the market price is below f*, then arbitrageurs would go long in the futures and short in the spot. • Example: Suppose Fm = 98. An arbitrageur would go long in the futures, agreeing to buy a 91 -day T-Bill for 98 seventy days later and would go short in the spot, borrowing the 161 -day T-Bill, selling it for 97. 5844 and investing the proceeds at 6. 38% for 70 days. Seventy days later (expiration), the arbitrageur would buy the bill (which now would have a maturity of 91 days) on the futures for 98 (fm), use the bill to close his short position, and collect 98. 74875 (f*) from his investment, realizing a cash flow of $7487.

Pricing T-Bill Futures • Note at fm = 98, a money market manager with a 161 -day TBill could earn an arbitrage by selling the bill for 97. 5844 and investing the proceed at 6. 38% for 70 days, then going long in the 70 -day T-Bill futures. Seventy days later, the money market manager would receive 98. 74875 from the investment and would pay 98 on the futures to reacquire the bill for a CF of. 74875.

Pricing T-Bill Futures • Implication: If the carrying-cost model holds, then the spot rate on a 70 -day bill (repo rate) will be equal to the synthetic rate (implied repo rate) formed by buying the 161 -day bill and going short in the 70 -day futures.

Pricing T-Bill Futures • Implication: If the carrying-cost model holds, then the YTM of the futures will be equal to the implied forward rate (F):

Hedging with T-Bill Futures • Case 1: Money market manager is expecting a $5 M CF in June which she plans to invest in a 91 -day T-Bill. With June T-Bill futures trading at IMM of 91, the manager could lock in a 9. 56% rate by going long in 5. 115 June T-Bill futures.

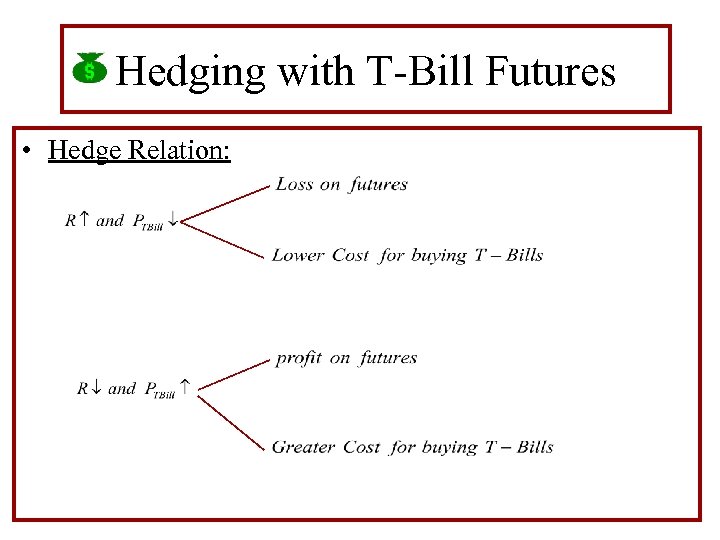
Hedging with T-Bill Futures • Hedge Relation:

Hedging with T-Bill Futures • Case 1: Suppose in June, the spot 91 -day T-bill rate is at 8%. The manager would find T-Bill prices higher at $980, 995 but would realize a profit of $17, 877 from closing the futures position. Combining the profit with the $5 M CF, the manager would be able to buy 5. 115 T-Bills and earn a rate off the $5 M investment of 9. 56%.

Hedging with T-Bill Futures • Case 1: Suppose in June, the spot 91 -day T-bill rate is at 10%. The manager would find T-Bill prices lower at $976, 518 but would realize a loss of $5, 025 from closing the futures position. After paying the CH $5, 025, the manager would still be able to buy 5. 115 T-Bills given the lower T-Bill prices, earning a a rate of return from the $5 M investment of 9. 56%.

Hedging with T-Bill Futures • Case 2: Money market manager is expecting a $5 M CF in June which she plans to invest in a 182 -day T-Bill. Since the T-Bill underlying a futures contract has a maturity of 91 days, the manager would need to go long in both a June T-Bill futures and a September T-Bill • futures (note there is approximately 91 days between the contract) in order to lock in a return on a 182 -day T-Bill investment. If June T-Bill futures were trading at IMM of 91 and September futures were trading at IMM of 91. 4, then the manager could lock in a 9. 3% rate on an investment in 182 -day T-Bills by going long in 5. 115 June T-Bill futures and 5. 11 September contracts:

Hedging with T-Bill Futures • Case 2: Suppose in June, the spot 91 -day T-bill rate is at 8% and the spot 182 -day T-Bill rate is at 8. 25%. At these rates, the price on the 91 -day spot T-Bill would be $980, 995, the price on the 182 -day spot would be $961, 245, and if the carryingcost model holds, the price on the September futures would be $979, 865. At these prices, the manager would be able to earn a profit of $24, 852 from closing both futures contract (which offsets the higher T-bill futures prices) and would be able to buy 5. 227 182 -day T-bills, yielding a rate of 9. 3% from a $5 M investment.

Hedging with T-Bill Futures • Case 2: Suppose in June, the spot 91 -day T-bill rate is at 10% and the spot 182 - day T-Bill rate is at 10. 25%. At these rates, the price on the 91 -day spot T-Bill would be $976, 518, the price on the 182 -day spot would be $952, 508, and if the carryingcost model holds, the price on the September futures would be $975, 413. At these prices, the manager would incur a loss of $20, 798 from closing both futures contracts. However, with lower T-bill futures prices, the manager would still be able to buy 5. 227 182 -day T-bills, yielding a rate of 9. 3% from a $5 M investment.

Managing the Maturity Gap • Case: In June, a bank makes a $1 M loan for 180 days which it plans to finance by selling a 90 -day CD now at the LIBOR of 8. 258% and a 90 -day CD ninety days later (in September) at the LIBOR prevailing at that time. To minimize its exposure to market risk, the bank goes short in 1. 03951 September Eurodollar futures at 92. 1 (IMM). By doing this, the bank is able to lock in a rate on its CD financing for 180 days of 8. 17%:

Managing the Maturity Gap • Case: In September, the bank will sell a new 90 -day CD at the prevailing LIBOR to finance its $1. 019758 M debt on the maturing CD plus (minus) any debt (profit) from closing its short September Eurodollar futures position. If the LIBOR rate is higher, the bank will have to pay greater interest on the new CD, but it will realize a profit on its futures which, in turn, will lower the amount of funds it needs to finance. On the other hand, if the LIBOR is lower, then the bank will have lower interest payment on its new CD, but it will also incur a loss on its futures position and therefore have more funds that need to be financed. • As shown in the exhibit, at September LIBOR’s of 7. 5% or 8. 7%, the bank’s total debt at the end of the 180 -day period will be $1, 039, 509 which equates to a rate of 8. 17%. • Note: This is true for any rate.

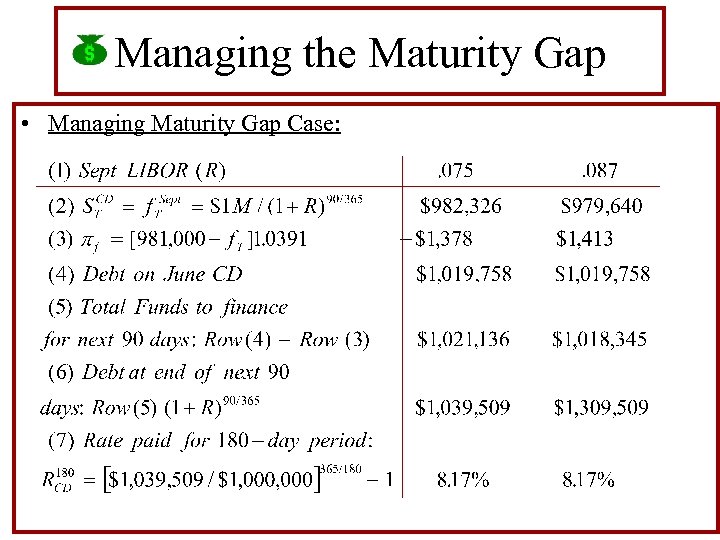
Managing the Maturity Gap • Managing Maturity Gap Case:

Fixing a Variable Rate Loan • Case: A construction company obtains a $1 M, one-year variable rate loan to finance one of its projects. The loan starts on 9/20 with the rate at 11. 25; the rate is then reset on 12/20, 3/20, and 6/20 at the prevailing LIBOR plus 150 BP. The company fixes the variable rate by going short in a series of Eurodollar futures (Eurodollar strip) with expirations of 12/20, 3/20, and 6/20 and the following prices:

Fixing a Variable Rate Loan • By doing this, the company is able to lock in a fixed rate of 10. 12%

Fixing a Variable Rate Loan • For example, if the LIBOR is at 9% on date 12/20, the company will have to pay $26, 250 on its loan the next quarter but it will also have a profit on its 12/20 Eurodollar futures of $1, 250 which it can use to defray part of the interest expenses, yielding an effective hedged rate of 10%.

Fixing a Variable Rate Loan • If the LIBOR is at 6% on date 12/20, the company will have to pay only $18, 750 on its loan the next quarter but it will also have to cover a loss on its 12/20 Eurodollar futures of $6, 250. The payment of interest and the loss on the futures yields an effective hedged rate of 10%.

Cross Hedge: Price-Sensitivity Model • Price-Sensitivity Model:

Hedging A Future CP Issue with T-Bills: Cross Hedge • Case: A company plans to sell a 182 -day CP issue with a $10 M principal in June to finance its anticipated accounts receivable. The company would like to lock in the current CP rate of 6%, ensuring it of funds from the CP sale of $9. 713635 M. Using the price-sensitivity model, the company locks in a rate by going short in 20 June T-bill futures contracts at IMM index = 95.

Hedging A Future CP Issue with T-Bills: Cross Hedge

Hedging A Future CP Issue with T-Bills: Cross Hedge • If CP sold at a discount yield that was 25 BP greater than the discount yield on T-Bills, then the company would be able to lock in a rate on its CP of 5. 48%.

Hedging A Future Bond Sale with T-Bond Futures: Cross Hedge • Bond portfolio manager plans to sell AA bond portfolio in June. Currently, the fund is worth $1. 02 M and has a YTM of 11. 76 and duration of 7. 36 years. • Using the price-sensitivity model to hedge the sale against a rate increase, the manager goes short in 15 June T-Bond contract trading at 72 - 16.

Options on Treasury Securities Hedging with Options on T-Bills and T-Bonds

T-Bill Options • Options on T-Bills give the holder the right to buy a T-Bill with a face value of $1 M and maturity of 91 days. • Exercise price is quoted in terms of the IMM index and the following formula can be used to determine X: • The option premium is quoted in terms of annual discount points (PT). The actual premium is

T- Bond Options • Options on T-Bonds give the holder the right to buy a specified T-Bond with a face value of $100, 000. • Exercise price is quoted as a percentage of par (e. g. IN = 90). If the holder exercises, she pays the exercise price plus the accrued interest: • The option premium is quoted in terms of points (PT). The actual premium is

Hedging with T-Bill Options Hedging $5 M CF in June with June T-Bill Call: • Call: X = IMM = 90; X = $975, 000; C = PT =. 5; C = $1250; Hedge: nc = $5 M/$975, 000 = 5. 128205; Cost = (5. 128205)($1250) = $6410.

Managing the Maturity Gap with T-Bill Put • Case: In June, a bank makes a $1 M loan for 180 days which it plans to finance by selling a 90 -day CD now at the LIBOR of 8. 258% and a 90 -day CD ninety days later (in September) at the LIBOR prevailing at that time. To minimize its exposure to market risk, the bank buys a T-Bill put at X = IMM = 90 for $$1250.

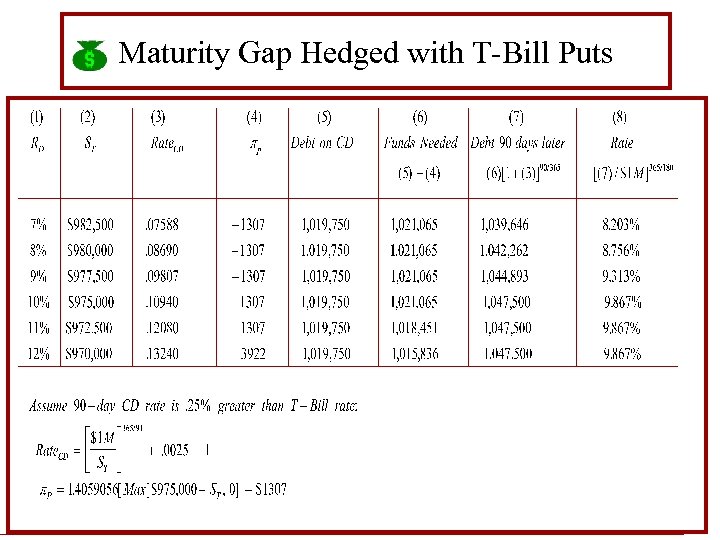
Maturity Gap Hedged with T-Bill Puts

Hedging future T-Bond Sale With T-Bond Puts • Case: Three months from the present (. 25 of year), a bond manager plans to sell a T-Bond with maturity of 15. 25 years, F = $100, 000, and coupon rate = 10%. • Manager hedges the sale against interest rate increases by buying one put option on a T-Bond with a current maturity of 15. 25 years and face value of $100, 000. The put has an expiration of T =. 25 years, exercise price of X = IN = 95 or X = $95, 000, and is trading at P = 1 - 5 or P = [1. 15625/100]($100, 000) = $1156.

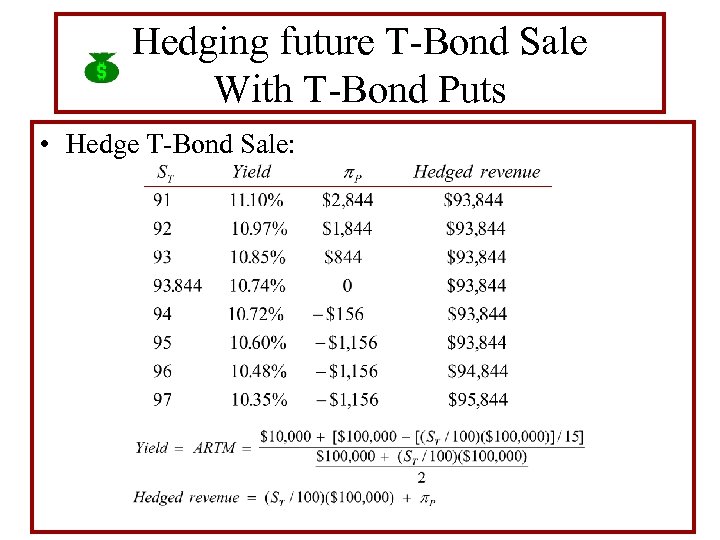
Hedging future T-Bond Sale With T-Bond Puts • Hedge T-Bond Sale:

Hedging Future Bond Portfolio Sale With T-Bond Puts • Case: Three months from the present (. 25 of year), a bond manager plans to liquidate a bond portfolio consisting of AAA, and A bonds. The portfolio currently has a WAM of 15. 25 years, F = $10 M, WAC = 10%, and has tended to yield a rate 1% above TBond rates. • Manager hedges the sale against interest rate increases by buying put options on a T-Bond with a current maturity of 15. 25 years and face value of $100, 000. The put has an expiration of T =. 25 years, exercise price of X = IN = 95 or X = $95, 000, and is trading at P = 1 - 5 or P = [1. 15625/100]($100, 000) = $1156. • To hedge, the manager buys 105. 26316 T-Bond puts for $121, 684:

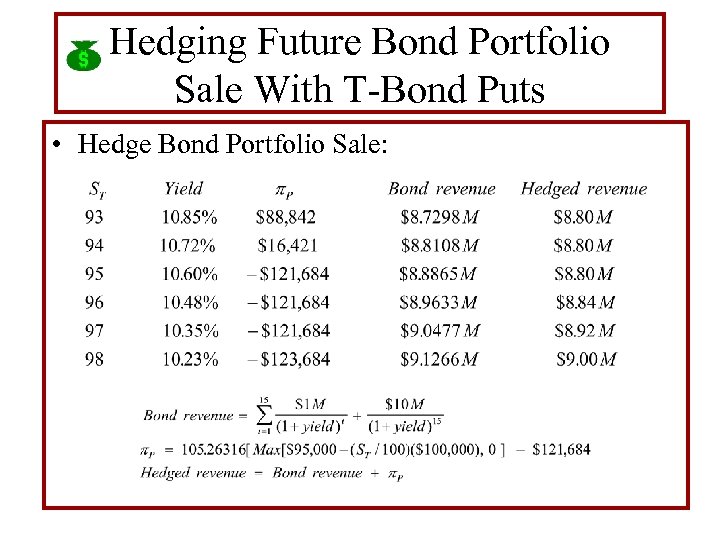
Hedging Future Bond Portfolio Sale With T-Bond Puts • Hedge Bond Portfolio Sale:

Futures Options on Treasury Securities • Futures options give the holder the right to take a futures position: – Futures Call Option gives the holder the right to go long. When the holder exercises, she obtains a long position in the futures at the current price, ft, and the assigned writer takes the short position and pays the holder ft - X. – Futures Put Option gives the holder the right to go short. When the holder exercises, she obtains a short position at the current futures price, ft, and the assigned writer takes the long position and pays put holder X - ft. • Futures option on Treasuries: Options on T-Bill Futures, T-Bond Futures, and T-Note Futures.

Futures Options on Treasury Securities Call on T-Bill Futures: • X = IMM 90 or X = $975, 000 • PT =. 5 or C = $1, 250 • Futures and options futures have same expiration.

Futures Options on Treasury Securities Put on T-Bill Futures: • X = IMM 90 or X = $975, 000 • PT =. 5 or P = $1, 250 • Futures and options futures have same expiration.

Futures Options on Treasury Securities Notes: • If the futures and the options on the futures expire at the same time and the carrying cost model holds, then the options on the spot and the options on the futures are equivalent. • Futures options are more liquid than spot options, making them more popular. • Hedging with Treasury futures options are similar to hedging with Treasury spot options.

Interest Rate Options

Interest Rate Options • Interest rate call option gives the holder the right to a payoff if an interest rate (e. g. , LIBOR) exceeds a specified exercise rate; interest rate put option gives the holder the right to a payoff if an interest rate is less than the exercise rate. • Interest rate options are written by commercial banks in conjunction with a future loan or CD investment.

Interest Rate Call Option Case: • A company plans to borrow $10 M in sixty days from Sun Bank. The loan is for 90 days with the rate equal to LIBOR in 60 days plus 100 BP. • Worried that rates could increase in the next 60 days, the company buys an interest rate call from the bank for $20, 000. • Terms: Exercise Rate = 7%; call premium plus interest will be paid at the maturity of the loan; any interest rate payoff will be paid at the loan’s maturity. • See JG, pp 522.

Interest Rate Put Option Case: • A company plans to invest $10 M in sixty days in a Sun Bank 90 -day CD. The CD will pay the LIBBER. • Worried that rates could decrease in the next 60 days, the company buys an interest rate put from the bank for $15, 000. • Terms: Exercise Rate = 7%; put premium plus interest will be paid at the maturity of the CD; any interest rate payoff will be paid at the CD’s maturity. • See JG, pp 522.

Caps: Series of Interest Rate Call Options • A Cap is a series of interest rate calls that expire at or near the interest rate payment dates on a loan. They are written by financial institutions in conjunction with a variable rate loan. Case: • A company borrow $50 M from Commerce Bank to finance its yearly construction projects. The loan starts on March 1 at 8% and is reset every three months at the prevailing LIBOR. • Cap: In order to obtain a maximum rate while still being able to obtain lower rates if the LIBOR falls, the company buys a Cap from the bank for $100, 000 with exercise Rate = 8%. • See JG, pp 524.

Floor: Series of Interest Rate Put Options • A floor is a series of interest rate puts that expire at or near the payment dates on a loan. They are purchased by financial institutions in conjunction with a variable rate loan they are providing. Case: • Commerce Bank purchases a floor with an exercise rate of 8% for $70, 000 from another institution to protect the variable rate loan it made. • See JG, pp 524.

Interest Rate Swaps

Interest Rate Swaps • An interest rate swap is an exchange of CFs. • Generic Interest Rate Swap involves the exchange of fixed-rate payments for floating-rate payments.

Interest Rate Swaps Terms: • Parties to a swap are called counterparties. There are two parties: – Fixed-Rate Payer – Floating-Rate Payer • Rates: – Fixed rate is usually a T-Note rate plus BP – Floating rate is usually the LIBOR.

Interest Rate Swaps Terms: • Interest is usually made semiannually. • Principal: Most interest rate swaps do not exchange principal. • Notional Principal: Interest is applied to a notional principal. • Maturity ranges between 3 and 5 years. • Dates: – Effective Date is the date interest begins to accrue – Payment Date is the date interest payments are made. • Only the interest differential is paid.

Interest Rate Swaps Example: • Fixed-rate payer pays 9. 5% every six months. • Floating-rate payer pays LIBOR every six months, • Notional Principal = $10 M. • Effective Dates are 3/23 and 9/23 for the next three years.

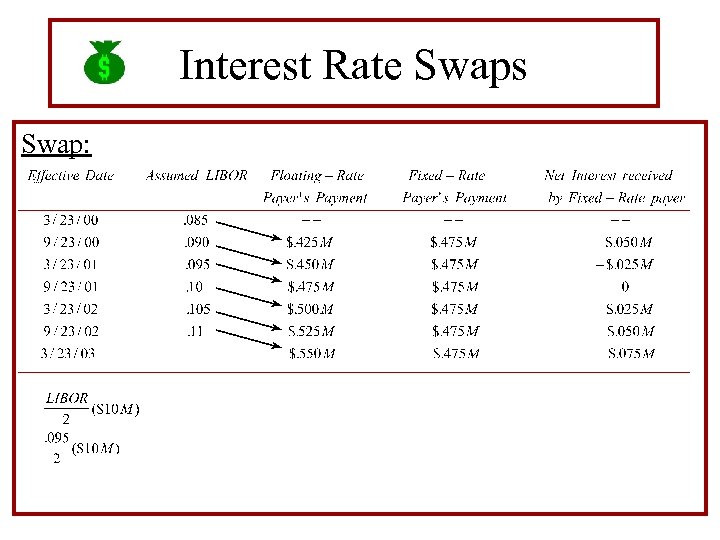
Interest Rate Swaps Swap:

Interest Rate Swaps Points: • If LIBOR > 9. 5%, then fixed payer receives the interest differential. • If LIBOR < 9. 5%, then floating payer receives the interest differential. • Fixed payer’s position is similar to a short position in Eurodollar strip. • Floating payer’s position is similar to a long position in a Eurodollar strip. See JG: 511 -512.

Interest Rate Swaps • A synthetic fixed-rate loan is formed by combining a variable rate loan with a fixed-rate payer’s position. • Example: A three-year, $10 M variable rate loan with rates set equal to the LIBOR on 3/23 and 9/23 combined with a fixed-rate payer’s position on the swap just analyzed.

Interest Rate Swaps Synthetic Fixed-Rate Loan:

Interest Rate Swaps • A synthetic variable-rate loan is formed by combining a fixed-rate loan with a floating-rate payer’s position. • Example: A three-year, $10 M, 9% fixed-rate loan combined with the floating-rate payer’s position on the swap just analyzed.

Interest Rate Swaps Synthetic Fixed-Rate Loan:

Interest Rate Swaps Points: • Swap Banks: The market for swaps is organized through a group of brokers and dealers collectively referred to as swap banks. – As brokers, swap banks try to match counterparties. – As dealers, swap banks temporary positions as fixed or floating players; often hedging their positions with positions in Eurodollar futures contracts.

Interest Rate Swaps Points: • Closing: Unlike futures positions, closing a swap position prior to maturity can be difficult. • Alternatives: – Sell Swap. – Enter offsetting swap position. – Hedge with Eurodollar futures.