Futures Futures Contract n A future contract

Futures

Futures Contract n A future contract is an agreement between to parties to buy or sell an asset at a certain time in future for a certain price. n n The buyer of the contract, who is said to be long the contract has agreed to buy (take delivery of) the goods in future. The seller is said to be short the contract and has obligation to sell (deliver) the goods in the future.

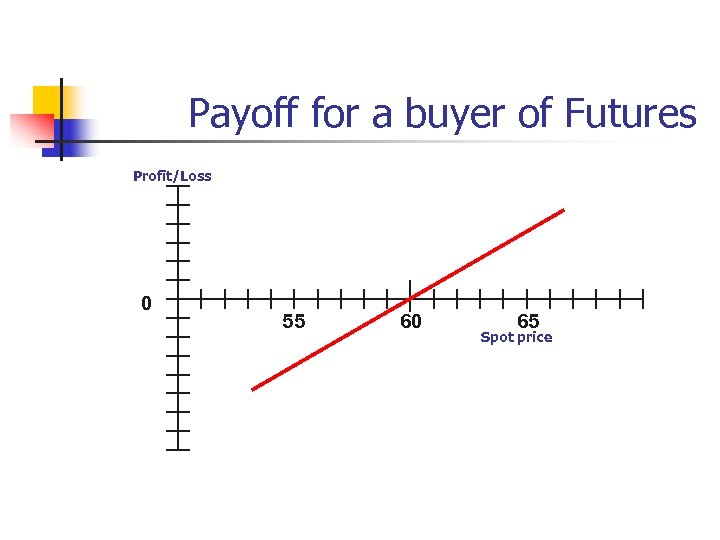Payoff for a buyer of Futures Profit/Loss 0 55 60 65 Spot price

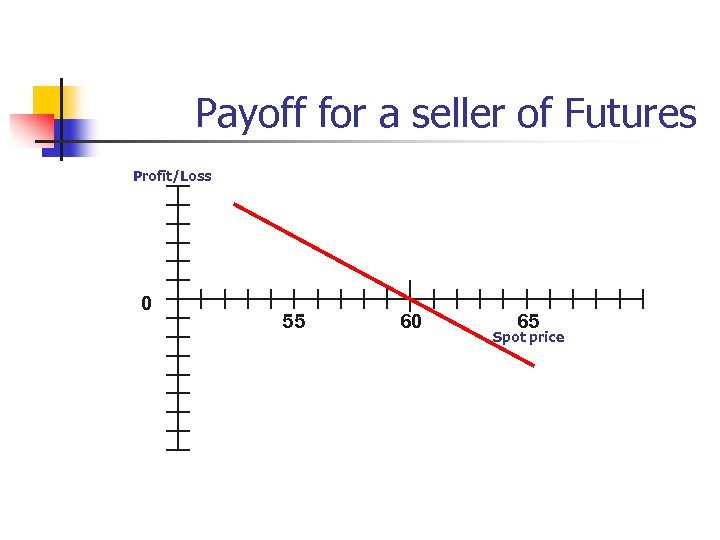Payoff for a seller of Futures Profit/Loss 0 55 60 65 Spot price

Futures Market in India n n Stock index futures launched on 12 th June, 2000 and stock futures in 9 th Nov, 2001. Futures on Stock Index and on individual stocks n n NSE: S&P CNX Nifty Futures, CNXIT Futures, BANK Nifty, CNX 100, CNX IT, CNX Nifty Junior, Nifty Midcap 50, futures on 207 individual stocks Commodity futures Currency futures Interest rate futures n NSE: Notional T – Bills, Notional 10 year bonds (coupon bearing and non-coupon bearing)

Futures Contract n n Exchange traded products. A standardized, transferable, exchangetraded contract that requires delivery of a commodity, bond, currency, or stock index, at a specified price, on a specified future date.

Forwards vs. Futures n A futures contract is like a forward contract: n n n Both specify that a certain commodity will be exchanged for another at a specified time in the future at prices specified today. They represent zero net supply; for every buyer there is a seller. Profit-loss profile realized in forwards and futures represent a zero sum game.

Forwards vs. Futures n A futures contract is different from a forward: n Futures are standardized; only the price in negotiated: e. g. all December 2004 gold futures contracts are identical in that the amount of gold (contract size), quality of gold, delivery date and place of delivery are specified. Forwards are customized and all the aspects can be negotiated.

Forwards vs. Futures n n Offesetting (prior to delivery date) a trade is possible in futures market while it is non-existent in most of the forward markets. For example, if you are long Dec 2004 gold futures contract you can close that position by later selling a Dec 2004 gold futures contract. Default risk is least in case of futures. Since forward contracts are agreements between the two parties, each part face the counterparty default risk.

Forwards vs. Futures n n Most future positions are eventually offset and in many cases they are cash settled. In contrast, most forward contracts terminate with delivery of the specified good. Margins and daily marking to market in case of futures.

Futures Contract: Standard Features n Contract specification n Asset type n n Contract size n n Exchange stipulates the grade of the asset. Specifies the amount of the asset to be delivered under one contract. Delivery agreement n The place of delivery

Futures Contract: Standard Features n Delivery months n n n Price quotes Daily price movement limits n n Futures are referred to by their delivery months. Daily price movement limits, termed as limit move (limit up and limit down) Position limits n Maximum number of contracts that a speculator may hold

Futures Contract: Standard Features n Clearing house n n Clearinghouse of the exchange becomes the opposite party to both buyers and sellers - thus guarantees the performance of the parties to each transaction. Margin requirement n When two parties trade a futures contract, the futures exchange requires some good faith money (security) from both, to act as a guarantee.

Futures Contract: Standard Features n Initial Margin n n Each exchange is responsible for setting the minimum initial margin requirements. The initial margin is the amount a trader must deposit into his trading account (also called as margin account) when establishing a position. Exchanges use SPAN (Standard Portfolio Analysis of Risk) to establish initial margin requirement.

Futures Contract: Standard Features n n Beyond the initial margin, if the equity in the account falls below a maintenance margin level, additional funds must be deposited to bring the account back up to the initial margin level. The process is known as margin call. The amount that is to be deposited is termed as variation margin. Once a trader has received the margin call, he must meet the call, even if the price has moved in his favour.

Futures Contract: Standard Features n For example, if the initial margin required to trade per gold futures contract is $1000, and the maintenance margin level is $750, then an adverse change of $2. 60/oz. will result in a margin call. Because one gold futures covers 100 oz. of gold a decline of $2. 60/oz in the futures price will deplete the long position by $260. The trader with losses must deposit sufficient funds to bring the margin to the initial level of $1000. The margin that is deposited to meet margin call is termed as variation margin.

Futures Contract: Standard Features n Types of orders n Market order n n Limit order n n Trade to be carried out immediately at the best price Specifies a particular price. The order can be executed only at this price or at one more favouarble to the investor. Stop order or stop-loss order n Also specifies a particular price. The order is executed at the best available price once a bid or offer is made at a particular price or a less favorable price.

Futures Contract: Standard Features n Stop-limit order n n Market-if-touched order n n A combination of stop order and limit order. They are like limit orders, except that they become market orders once a trade has occurred at the specified price. Discretionary order/Market-not-held order n Traded as a market order except that execution may be delayed at the broker's discretion in an attempt to get a better price.

Futures Contract: Standard Features n Time orders n n Unless specified, an order is a day order and expires at the end of the trading day. Good-till-cancelled remains active till executed or cancelled by the customer. Some other time orders are Good-thisweek, Good-this-month etc. Spread order n Specifies two trades that must be filled together. The order can specify a difference in the prices or it can be a market order.

Futures Contract: Standard Features n Offsetting the positions (squaring up) n n Most traders choose to close out their position prior to delivery period specified in the contract by entering into the opposite type of the trade. Open Interest n n Total number of contracts outstanding for a particular delivery month. Open interest is a good proxy for demand for a contract.

Futures Contract: Standard Features n Settlement n n n Physical settlement vs. Cash settlement Settlement month Settlement price

Futures Contract: Standard Features n Marking to Market n n n All futures traders’ positions are marked to market daily. Also known as daily resettlement. It means everyday, profits are added to, or losses are deducted from the trader’s account. Profits and losses are based on the changes in the settlement prices or closing futures prices.

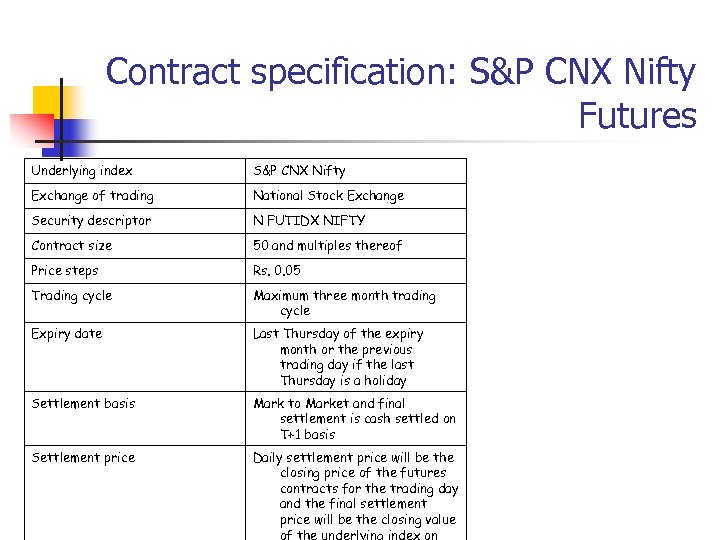Contract specification: S&P CNX Nifty Futures Underlying index S&P CNX Nifty Exchange of trading National Stock Exchange Security descriptor N FUTIDX NIFTY Contract size 50 and multiples thereof Price steps Rs. 0. 05 Trading cycle Maximum three month trading cycle Expiry date Last Thursday of the expiry month or the previous trading day if the last Thursday is a holiday Settlement basis Mark to Market and final settlement is cash settled on T+1 basis Settlement price Daily settlement price will be the closing price of the futures contracts for the trading day and the final settlement price will be the closing value of the underlying index on

Futures Contract: Standard Features n Marked to Market: An example n In NSE all future contracts are marked to market to the daily settlement price. The profit loss are computed as thus: n n n The trade price and the day’s settlement price for contracts executed during the day but not squared up Previous’ days settlement price and the current day’s settlement price for brought forward contracts Buy price and the sell price for contracts executed during the day and squared up

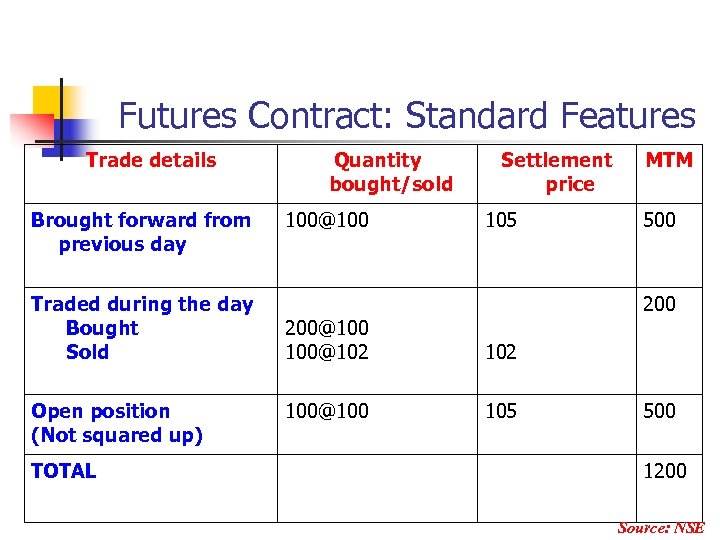Futures Contract: Standard Features Trade details Brought forward from previous day Traded during the day Bought Sold Open position (Not squared up) TOTAL Quantity bought/sold 100@100 Settlement price 105 MTM 500 200@100 100@102 100@100 105 500 1200 Source: NSE

Basis and Convergence n n Basis and convergence explain the relationship between futures price and cash price. Basis n n n Spot price (cash price) minus the futures price In a normal market basis will be negative; since future prices exceed spot prices and it is positive in an inverted market. Basis approaches zero as the delivery month is approached.

Basis and Convergence The process of basis moving towards zero is termed as convergence. Why does it happen? n It is due to arbitrage. For example, if future price is above spot price during the delivery period, the trader can n i. iii. Short a futures contract Buy the asset Make delivery

Pricing Futures n n n Do the quoted prices reflect true value of the underlying index? Does there exist any opportunity for arbitrage? Why should the basis be negative in normal markets? The dynamics lies in the Cost-of-carry model.

Cost of Carry Model n n Cost of carry measures the storage cost, plus the interest that is paid to finance the asset less the income earned on the asset. Cost of carry varies across the assets. n n For a non-dividend paying stock, the cost of carry is the risk free rate because there are no storage costs and no income is earned. For a commodity, storage cost is important.

Cost of Carry Model n The fair value of futures incorporates the ‘no -arbitrage’ limits on the prices. This is as thus F = S + CC - CR n n F = Future prices S = Spot price CC = Holding costs or carry costs. CR = Carry returns

Cost of Carry Model n For the stock index futures it can be mentioned as H(0, T) = r. T/365, where r is the annual interest rate, T is the number of days until delivery date and [FV(divs)] is the future value of all dividends paid by the component of the stock index

Cost of Carry Model n If n n traders will engage in a cash-and-carry arbitrage which calls for buying the spot index (it is relatively cheap) , ‘carrying‘ it, and selling the futures (relatively expensive). If n Traders will engage in a reverse cash-and-carry arbitrage which calls for buying the futures and selling the spot, and investing the proceeds.

Normal Backwardation and Contango n Normal backwardation n n Futures prices are below expected future spot prices, and futures price is expected to rise as the delivery date approaches Contango n A contango exists wherever the futures price lies above the expected future spot price, and the futures price generally declines as the delivery date nears.

Synthetic Stock and T Bills n n Buying a stock index futures contract and buying Treasury bills is frequently called a long synthetic stock position. Buying shares of stock that replicates an index and also selling a futures contract on the stock creates a synthetic treasury bill.

Synthetic Stock n Illustration n An investor owns $9, 523, 800 in one year T-bills which will be worth $10 million one year hence. Take long position in stock index futures with an underlying value equal to $9, 523, 800 (based on spot index). Suppose that index futures price is 1375 and the spot is at 1325 and the futures contract multiplier is 250.

Synthetic Stock n n 28. 7511 futures will be purchased ($9, 523, 800/1325*250 ) Now suppose after one year spot price and futures price are at 1500. The value of the portfolio is n n n $10 million from T bills $898, 472 in stock index futures profit (125 × 250 × 28. 7511) Gain is 14. 434%, given that investor began the year with $9, 523, 800

Synthetic Stock n n The 14. 434% is identical to the return from buying actual stocks, ignoring transaction costs. The capital appreciation on the stock was 13. 208%. (1500 -1325/1325) Had he purchased the stocks he would have received the dividends and interest on those dividends, and this dividend yield component would have been 1. 2264%. Total return is 14. 434%

Synthetic T bill n n The arbitrageur buys the stock and locks in a selling price by selling futures contract. When performing a cash-and-carry arbitrage, the synthetic T-bill is created by borrowing at a lower rate and lending at a higher rate, which is risk less.

Hedging with Futures n n n Hedgers use futures market to reduce a particular risk that they face. A perfect hedge is one that completely eliminates the risk. In practice, these are rare. When is the short futures position appropriate? When is a long futures position appropriate? Which futures contract should be used? What is the optimal size of the futures position?

Hedging: The Basic Principle n The objective is usually to take a position that neutralizes the risk as far as possible. n Consider an investor who will gain Rs. 10, 000 for each rupee increase in the price of the commodity over the next three months and lose Rs. 10, 000 for each rupee decrease in the price during the same period. To hedge, the investor should take a short futures position that is designed to offset the risk.

Hedging with Futures n Short hedge n n n Involves a short position in futures contract. Appropriate when the hedger has already owned the asset and expects to sell it in future. Can also be used when an asset is not owned right now but will be owned at some time in future.

Hedging with Futures n Short hedge illustration n On May 15, 2004 an oil produces negotiated a contract to sell 1 million barrels of crude oil. It has been argued that price that will apply in the contract is the market price on August 15. The oil producer is therefore in the position where it will gain $10, 000 for each cent increase in the price and lose $10, 000 for each cent decrease in the price.

Hedging with Futures n n n Suppose that spot price on May 15 is $19 per barrel and August crude oil futures price is $18. 75 per barrel. Each futures contract involves the delivery of 1000 barrels. The company can hedge by shorting 1000 August futures contracts. If the oil producer closes out his position on August 15, the effect of the strategy should be to lock in a price close to $18. 75 per barrel.

Hedging with Futures n Long hedge n n Long positions in a futures contract More appropriate when one needs to purchase a certain asset in the future and wants to lock in a price now.

Hedging with Futures n Long hedge illustration n n On January 15 a copper fabricator knows it will require 100, 000 pounds of copper on May 15 to meet certain contracts. The spot price of the copper is 140 cents per pound, and the May futures are priced at 120 cents per pound. Each contract is for the delivery of 25, 000 pounds of copper. The fabricator can hedge his position by taking a long position in four May futures contract.

Hedging with Stock Index Futures n Long security – Short index futures n n n Every buy position on a security is simultaneously a buy position on the index. As a way out a long position on a security can be accompanied by sale of index futures. One needs to know the beta of a security.

Hedging with Stock Index Futures n Illustration n Shyam adopts a position of Rs. 1 million LONG MTNL on date 5 th June 2001. He plans to hold the position till the 25 th. Suppose the beta of MTNL happens to be 1. 2. Hence he needs a short position of Rs. 1. 2 million on the index futures market to totally remove his Nifty exposure.

Hedging with Stock Index Futures n n On date 5 th June 2001, Nifty is 980 and the nearest futures contract (with expiration 28 th June 2001) is trading at about 1000. Hence, each market lot of the futures (200 nifties) is worth Rs. 200, 000. To sell Rs. 1. 2 million of Nifty, we need to sell 6 lots (by rounding off to the nearest market lot). He sells 6 market lots of Nifty (1200 nifties) to get the position: LONG MTNL Rs. 1, 000 SHORT NIFTY Rs. 1, 200, 000

Hedging with Stock Index Futures n n 10 days later, Nifty crashed because of instability in the government. On Thursday, Shyam unwound both positions. His position on MTNL lost Rs. 120, 000 since MTNL had dropped to 880, 000. His short position on Nifty June futures earned Rs. 141, 600. Overall, he earned Rs. 21, 600.

Hedging with Stock Index Futures n Short security – Long index futures n n n Every sell position on a security is a simultaneous sell position on the index. A short position on a security must be accompanied by a long position on the index futures. A knowledge of beta is essential.

Hedging with Stock Index Futures n Illustration n Shyam adopts a position of Rs. 1 million SHORT MTNL on date 1 st April 1997. He plans to hold the position till Thursday the 24 th. The beta of MTNL happens to be 1. 2. Hence he needs a long position of Rs. 1. 2 million on the index futures market to totally remove his Nifty exposure.

Hedging with Stock Index Futures n n On date 1 st April 97, Nifty is 980 and the nearest futures contract (with expiration 24 th April) is trading at about 1000. Hence, each market lot of the futures (200 nifties) is worth Rs. 200, 000. To buy Rs. 1. 2 million of Nifty, we need to buy 6 lots (by rounding off to the nearest market lot). He buys 6 market lots of Nifty (1200 nifties) to get the position: SHORT MTNL Rs. 1, 000 LONG NIFTY Rs. 1, 200, 000

Hedging with Stock Index Futures n n 20 days later, Nifty rose because of stable political outlook. On Thursday, Shyam unwound both positions. His position on MTNL lost Rs. 120, 000 since MTNL had gone up to 1, 120, 000. His short position on Nifty April futures earned Rs. 93, 600. Overall, he lost Rs. 26, 400.

Hedging with Stock Index Futures n Have portfolio – short index futures n n n Every portfolio contains hidden index exposure. Exposure can be minimized by using index futures. Knowledge of beta of the portfolio is essential.

Hedging with Stock Index Futures n Illustration n On 25 May 2001, Shyam has a portfolio composed of five securities: ITCHOTEL (100 shares, value Rs. 112. 00), ORIENTBANK (200 shares, value Rs. 68. 25), CIPLA (100 shares, value Rs. 847. 65), LUPINLAB (200 shares, value Rs. 149. 85), and SIEMENS (200 shares, value Rs. 237. 50). The total portfolio value is 187, 085 and the fi ve securities have weights (5. 98%, 7. 29%, 45. 31%, 16. 02%, 25. 40%). Shyam does not want to worry about budget-related fluctuations from 26 May 2001 till 10 June 2001.

Hedging with Stock Index Futures n n The five securities have the following betas: ITCHOTEL (beta 0. 59), ORIENTBANK (beta 0. 90), CIPLA (beta 0. 75), LUPINLAB (beta 1. 13), and SIEMENS (beta 1. 10). Hence the portfolio beta works out to (0. 0598*0. 59 + 0. 0729*0. 90 + 0. 4531*0. 75 + 0. 1602*1. 13 + 0. 2540*1. 10) or 0. 90. For complete hedging he will need to sell futures worth 0. 90 * 187, 085, i. e. Rs. 168, 376. 50. On 25 May 2001, Nifty is at 1, 122. 95. So he decides to sell 200 Nifties.

Hedging with Stock Index Futures n n Hence Shyam supplements his portfolio with a short position on the Nifty futures with expiry on 25 th JUNE worth Rs. 224, 590. On 10 June he buys back futures at a lower price and ends his hedge (see Table 5. 1). His profits on the futures hedging was Rs. 32, 010 and his losses on the portfolio were Rs. 32, 990. Thus the net loss is Rs. 980. If he had not hedged, he would have lost 32, 990.

Hedging with Stock Index Futures n Have funds – Long index futures n Index futures can be used to hedge against a rise in the index.

Hedging with Stock Index Futures n Illustration n n Iqbal obtained Rs. 5 million on 17 Feb 1998. He made a list of 14 securities to buy, at 17 Feb prices, totaling Rs. 5 million. At that time Nifty was at 991. 70. He entered into a LONG NIFTY MARCH FUTURES position for 5000 nifties, i. e. his long position was worth 5, 053, 600. From 18 Feb 1998 to 09 March 1998 he gradually acquired the securities (see Table 5. 2). On each day, he purchased one securities and sold off a corresponding amount of futures.

Hedging with Stock Index Futures n n On each day, the securities purchased were at a changed price (as compared to the price prevalent on 17 Feb). On each day, he obtained or paid the ‘mark–to–market margin’ on his outstanding futures position, thus capturing the gains on the index. By 09 Mar 1998 he had fully invested in all the shares that he wanted (as of 17 Feb) and had no futures position left. The same sequencing of purchases, without the umbrella of protection of the LONG NIFTY MARCH FUTURES position, would have cost Rs. 249, 724 more.

Speculation with Index Futures n Bullish index – Long nifty futures n n n n On 1 July 2001, Milan feels the index will rise. He buys 200 Nifties with expiration date on 31 st July 2001. At this time, the Nifty July contract costs Rs. 960 so his position is worth Rs. 192, 000. On 14 July 2001, Nifty has risen to 967. 35. The Nifty July contract has risen to Rs. 980. Milan sells off his position at Rs. 980. His profits from the position are Rs. 4000.

Speculation with Index Futures n Bearish index – Short nifty futures n n n On 1 June 2001, Milan feels the index will fall. He sells 200 Nifties with a expiration date of 26 th June 2001. At this time, the Nifty June contract costs Rs. 1, 060 so his position is worth Rs. 212, 000. On 10 June 2001, Nifty has fallen to 962. 90. The Nifty June contract has fallen to Rs. 990. Milan squares off his position. His profits from the position work out to be Rs. 14, 000.

Index Arbitrage n A strategy designed to profit from temporary discrepancies between the prices of the stocks comprising an index and the price of a futures contract on that index. By buying either the stocks or the futures contract and selling the other, an investor can sometimes exploit market inefficiency for a profit. Like all arbitrage opportunities, index arbitrage opportunities disappear rapidly once the opportunity becomes well-known and many investors act on it.

Index Arbitrage n n Index arbitrage can involve large transaction costs because of the need to simultaneously buy and sell many different stocks and futures, and so only large money managers are usually able to profit from index arbitrage. In addition, sophisticated computer programs are needed to keep track of the large number of stocks and futures involved, which makes this a very difficult trading strategy for individuals. Programme Trading n Trading a stock portfolio in a single order

Index Arbitrage n Suppose i. e n How does one carry index arbitrage? n Cash and Carry arbitrage

Index Arbitrage TODAY n n n Buy the component of the index in the appropriate weights, so that index is replicated Borrow the forgoing amount for the number of days until the delivery date, at an annual interest rate of r% (h% annualized) Sell one futures contract at its current futures price (F 0) Total Cash Flow - S 0 + S 0 0 0

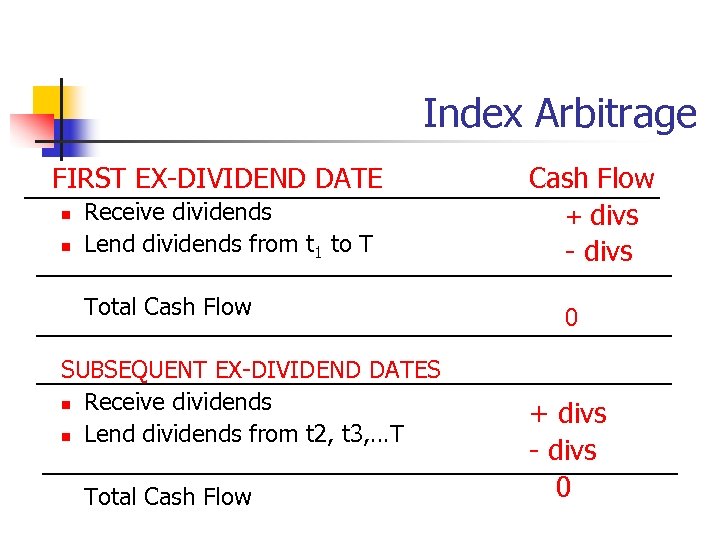Index Arbitrage FIRST EX-DIVIDEND DATE n n Receive dividends Lend dividends from t 1 to T Total Cash Flow SUBSEQUENT EX-DIVIDEND DATES n Receive dividends n Lend dividends from t 2, t 3, …T Total Cash Flow + divs - divs 0

Index Arbitrage ON THE DELIVERY DATE n n Offset the futures contract Sell the stocks Repay loan and interest Receive dividends and interest on dividends Total Cash Flow F 0 – FT = F 0 – ST ST -S 0 – h(0, T)S 0 FV(divs)

Arbitrage with Index Futures n n n On 1 August, Nifty is at 1200. A futures contract is trading with 27 August expiration for 1230. Ashish wants to earn this return (30/1200 for 27 days). He buys Rs. 3 million of Nifty on the spot market. In doing this, he places 50 market orders and ends up paying slightly more. His average cost of purchase is 0. 3% higher, i. e. he has obtained the Nifty spot for 1204. He takes delivery of the shares and waits.

Arbitrage with Index Futures n n n While waiting, a few dividends come into his hands. The dividends work out to Rs. 7, 000. On 27 August, at 3: 15, Ashish puts in market orders to sell off his Nifty portfolio, putting 50 market orders to sell off all the shares. Nifty happens to have closed at 1210 and his sell orders (which suffer impact cost) goes through at 1207. The futures position spontaneously expires on 27 August at 1210 (the value of the futures on the last day is always equal to the Nifty spot).

Arbitrage with Index Futures Ashish has gained Rs. 3 (0. 25%) on the spot Nifty and Rs. 20 (1. 63%) on the futures for a return of near 1. 88%. n In addition, he has gained Rs. 7000 or 0. 23% owing to the dividends for a total return of 2. 11% for 27 days, risk free. n

Optimal hedge ratio n n n Hedge ratio represents the ratio of the size of the position taken in futures contracts to the size of the exposure. Optimal hedge ratio may differ from 1. The optimal hedge ratio (h*) is given as n n S = Standard deviation of change in spot price F = Standard deviation of change in futures price = Correlation coefficient between spot price and futures price Optimal hedge ratio is also termed as Minimum variance hedge ratio.

Optimal hedge ratio n Optimal number of futures contracts is given as thus: n n n NA = Size of the position being hedged (units) QF = Size of the futures contracts (units) N* = Optimal number of futures contracts for hedging

Optimal hedge ratio and Beta n n n Stock index futures can be used to hedge an equity portfolio. If the portfolio mirrors the index, a hedge ratio of 1. 0 is appropriate. When the portfolio does not exactly match the index, beta from the CAPM can be used to determine the appropriate hedge. This is as thus n n P = Current value of the portfolio A = Current value of the stocks underlying one futures contract

Beta Management n Portfolio managers adjust their portfolio betas to reflect changes in the perceived market risk and return n Bullish expectation increase beta (increase the exposure to the market) Bearish expectation decrease beta (decrease the exposure to the market) How to adjust beta? n n Reduce beta by selling part of an equity portfolio and buy risk less securities Increase beta make additional investments on risky equity portfolio through borrowing/selling risk less securities

Beta Management n Adjust beta by using stock index futures n n Sell stock index futures to reduce exposure to market risk Buy stock index futures to have additional exposure to market risk See illustration

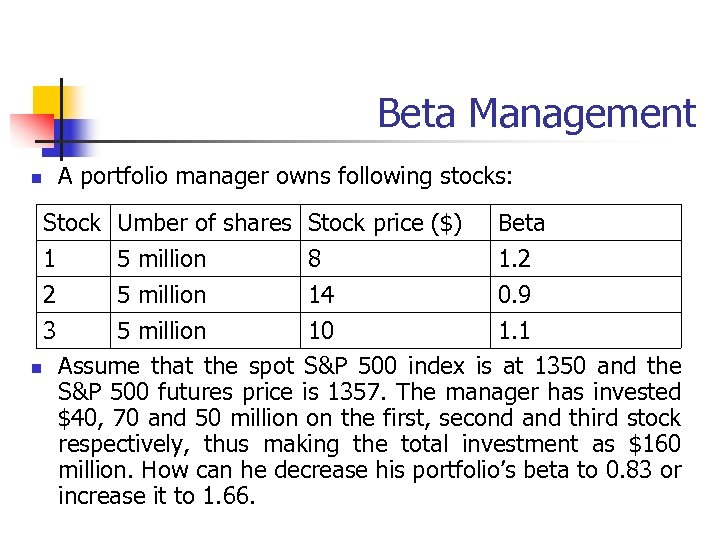Beta Management n A portfolio manager owns following stocks: Stock Umber of shares Stock price ($) Beta 1 5 million 8 1. 2 2 5 million 14 0. 9 3 5 million 10 1. 1 n Assume that the spot S&P 500 index is at 1350 and the S&P 500 futures price is 1357. The manager has invested $40, 70 and 50 million on the first, second and third stock respectively, thus making the total investment as $160 million. How can he decrease his portfolio’s beta to 0. 83 or increase it to 1. 66.

Beta Management n Decreasing the current beta from 1. 0375 to 0. 83 n n Define the current portfolio of equities to be asset 1 and the risk less security to be asset 2. The desired portfolio beta is 0. 83. Thus Therefore, a portfolio consisting of $128 million (0. 80 × $160 million) invested in our portfolio of three risky equities, and $32 million in T bills would create a portfolio with a beta of 0. 83 (0. 80 × 1. 0375 + 0. 20 × 0).

Beta Management n n Size of the position being hedged = $32, 000 (=$32, 000 / 1350 = 23703. 7 units) Size of one futures contract = 250 Beta of the portfolio = 1. 0375 Optimal number of futures contracts = 98. 370355

Interest Rate Futures

Interest Rate Futures n Long term interest futures n n n Short term interest rate futures n n n T-Bond futures T-note futures T-Bill futures contract Eurodollars Indian markets n n n Futures contract on Notional 91 day T bill Futures contract on Notional 10 year coupon bearing bond Futures contract on Notional 10 year zero coupon bond.

T-Bond Futures n n The US Treasury Bond contracts at the CBOT Contract size n n Deliverable grades n n U. S. Treasury bonds that, if callable, are not callable for at least 15 years from the first day of the delivery month or, if not callable, have a maturity of at least 15 years from the first day of the delivery month. The invoice price equals the futures settlement price times a conversion factor plus accrued interest. Tick size n n One U. S. Treasury bond having a face value at maturity of $100, 000 or multiple thereof and coupon rate being 6%. 1/32 of a point ($31. 25/contract) Contract months n Mar, Jun, Sep, Dec

T-Note Futures (10 yrs) n n One U. S. Treasury note having a face value at maturity of $100, 000 or multiple thereof. Deliverable grades n n Tick size n n One half of 1/32 of a point ($15. 625/contract) Contract months n n U. S. Treasury notes maturing at least 6 1/2 years, but not more than 10 years, from the first day of the delivery month. Mar, Jun, Sep, Dec CBOT also trades on 5 -yr and 2 -yr Treasury note futures

Interest Rate Futures (IRF) in NSE n IRF underlyings in NSE n n n Notional T – Bills (91 day) Notional 10 year bonds (coupon bearing and non -coupon bearing) Trading cycle n The interest rate future contract shall be for a period of maturity of one year

Interest Rate Futures (IRF) in NSE n Expiry day n n Interest rate future contracts shall expire on the last Thursday of the expiry month. If the last Thursday is a trading holiday, the contracts shall expire on the previous trading day. Further, where the last Thursday falls on the annual or half-yearly closing dates of the bank, the expiry and last trading day in respect of these derivatives contracts would be pre-poned to the previous trading day.

Interest Rate Futures (IRF) in NSE n Contract size n n The permitted lot size for the interest rate futures contracts shall be 2000. The minimum value of a interest rate futures contract would be Rs. 2 lakhs at the time of introduction. The price steps in respect of all interest rate future contracts admitted to dealings on the Exchange is Re. 0. 01.

Interest Rate Futures (IRF) in NSE n Settlement procedure and settlement price n n Daily Mark to Market settlement and Final Mark to Market settlement in respect of admitted deals in Interest Rate Futures Contracts shall be cash settled by debiting/ crediting of the clearing accounts of Clearing Members with the respective Clearing Bank. All positions (brought forward, created during the day, closed out during the day) of a F&O Clearing Member in Futures Contracts, at the close of trading hours on a day, shall be marked to market at the Daily Settlement Price (for Daily Mark to Market Settlement) and settled.

Interest Rate Futures (IRF) in NSE n n n All positions (brought forward, created during the day, closed out during the day) of a F&O Clearing Member in Futures Contracts, at the close of trading hours on the last trading day, shall be marked to market at Final Settlement Price (for Final Settlement) and settled. Daily settlement price shall be the closing price of the relevant Futures contract for the Trading day. Final settlement price for an Interest rate Futures Contract shall be based on the value of the notional bond determined using the zero coupon yield curve computed by National Stock Exchange or by any other agency as may be nominated in this regard.

Conversion Factor and Invoice Amounts n n The invoice amount, or invoice price, is the amount the short is paid, should they choose to deliver. He invoice amount equals the futures settlement price times a ‘conversion factor’ plus ‘accrued interest’.

Conversion Factor n Conversion factor n n Conversion factor for a given bond is the value of the bond per dollar/rupee of face value as calculated on the first day of the delivery month, using an annual YTM of 6% and semi-annual compounding (T-bond futures). Conversion factor (price factor) gives the price of an individual cash bond such that its YTM on the delivery day is equal to the notional coupon of the contract.

Accrued Interest n Accrued interest

Computing the Conversion Factor n n n Assume it is the first day of the delivery month, and calculate the time to maturity of the bond. Round down this time to maturity to the nearest three-month period. For example, 18 years and 5. 5 months becomes 18 years and 3 months. If after rounding off the life of the bond is an integer multiple of semi-annual periods, then the first coupon is assumed to be paid after 6 months, otherwise assumed to be paid after 3 months.

Conversion Factor Example I n n n We are short in a June futures contract and that today is June 1, 2001. Consider a 7% T-bond that matures on 15 June, 2029 which is eligible for delivery under the futures contract. On June 1, this bond has 28 years and 1. 5 months to maturity. When rounded off to the nearest three months, we get a figure of 28 years. The first coupon is then assumed to be paid after six months

Conversion Factor Example I n The conversion factor is calculated as below:

Conversion Factor Example II n n Instead of the July 2029 bond, consider another bond that is maturing on 15 September, 2029. On June 1, 2001, this bond has 28 years and 3. 5 months to maturity. The life of the bond, when rounded off to the nearest three months, is 28 yrs and 3 months. First coupon is assumed to be paid after three months.

Conversion Factor Example II n n n First the price of the bond three months from today, using a yield 6% is calculated. Discount the price for another three months. Subtract the accrued interest for three months, from the price obtained above.

Invoice Price n n n Let us assume that on 15 June, 2001 the 7% bond maturing on 15 September, 2029 will be delivered under June contract. The actual delivery will be made two days later, that is, on 17 June. How to calculate the invoice price?

Invoice Price n n The last coupon would have been paid on 15 March, 2001 and the next will be due on 15 September, 2001. Accrued interest for a T-bond with face value of $100, 000 is The futures settlement price on 15 June is assumed to be 95 -12. This corresponds to a decimal futures price per dollar of the face value of

Invoice Price n Invoice price

T-Bond Futures Prices n n Cost-of-Carry model determines the T-Bond futures prices. Because the short gets to choose which bond to deliver, the futures price will reflect the spot price (S) of the bond that the market expects the short to select. This is called Cheapest-to-Deliver (CTD) bond. The carry cost (CC) is the interest rate changes incurred when an trader borrows to buy the CTD. Carry return (CR) is the accrued interest, actual coupon payments and the interest on coupons, if any.

Cheapest to Deliver T-Bond n During the delivery month the CTD is determined by computing the cost and the invoice amount. CTD is one that maximizes the inflows and minimizes the outflows for the short. n n CTD = max [invoice amount – (spot price + accrued interest)] Before the delivery period, we can only estimate which T-Bond will likely to be the CTD.

Cheapest to Deliver T-Bond n Implied repo rate (IRR) n IRR is the rate of return earned by buying the deliverable spot asset and simultaneously selling a futures contract. Thus

Cheapest to Deliver T-Bond n Using duration n n If yields are above 6%, the CTD bond will be the eligible bond with highest duration. If yields are below 6%, the CTD bond will be the eligible bond with the lowest duration.

T-Bill Futures Contracts n Exchange n n Underlying n n International Money Market (IMM) segment of Chicago Mercantile Exchange (CME) 3 -month US T-bills having a face value at maturity of $1 million. Delivery dates n March, June, September and December

Eurodollar Futures n Underlying n n 3 month time deposits in dollars at banks located outside the US mainly in Europe and in particular, in London. Cash settled