Futures and Options on Foreign Exchange Chapter Seven

Futures and Options on Foreign Exchange Chapter Seven Copyright © 2012 by the Mc. Graw-Hill Companies, Inc. All rights reserved.

Chapter Outline § § § Futures Contracts: Preliminaries Currency Futures Markets Basic Currency Futures Relationships Options Contracts: Preliminaries Currency Options Markets Currency Futures Options Basic Option Pricing Relationships at Expiry American Option Pricing Relationships European Option Pricing Relationships Binomial Option Pricing Model European Option Pricing Model Empirical Tests of Currency Option Models 7 -2

Futures Contracts: Preliminaries § A futures contract is like a forward contract in that it specifies that a certain currency will be exchanged for another at a specified time in the future at prices specified today. § A futures contract is different from a forward contract in that futures are standardized contracts trading on organized exchanges with daily resettlement through a clearinghouse. 7 -3

Futures Contracts: Preliminaries § Standardizing features: – Contract size – Delivery month – Daily resettlement § Initial performance bond (about 2 percent of contract value, cash or T-bills, held in a street name at your brokerage) 7 -4

Daily Resettlement: An Example § Consider a long position in the CME Euro/U. S. Dollar contract. § It is written on € 125, 000 and quoted in $ per €. § The strike price is $1. 30 per € the maturity is 3 months. § At initiation of the contract, the long posts an initial performance bond of $6, 500. § The maintenance performance bond is $4, 000. 7 -5

Daily Resettlement: An Example § With futures contracts, we have daily resettlement of gains and losses rather than one big settlement at maturity. § Every trading day: – If the price goes down, the long pays the short. – If the price goes up, the short pays the long. § After the daily resettlement, each party has a new contract at the new price with oneday-shorter maturity. 7 -6

Performance Bond Money § Each day’s losses are subtracted from the investor’s account. § Each day’s gains are added to the account. § In this example, at initiation the long posts an initial performance bond of $6, 500. § The maintenance level is $4, 000. – If this investor loses more than $2, 500, he has a decision to make; he can maintain his long position only by adding more funds, and if he fails to do so his position will be closed out with an offsetting short position. 7 -7

Daily Resettlement: An Example § Over the first 3 days, the euro strengthens then depreciates in dollar terms: Settle Gain/Loss Account Balance $1. 31 $1, 250 = ($1. 31 – $1. 30)× 125, 000 + $1, 250 $7, 750 = $6, 500 $1. 30 –$1, 250 $6, 500 $1. 27 –$3, 750 $2, 750 + $3, 750 = $6, 500 On day three suppose our investor keeps his long position open by posting an additional $3, 750. 7 -8

Daily Resettlement: An Example § Over the next 2 days, the long keeps losing money and closes out his position at the end of day five. Settle $1. 31 $1. 30 $1. 27 $1. 26 $1. 24 Gain/Loss $1, 250 –$3, 750 –$1, 250 –$2, 500 Account Balance $7, 750 $6, 500 $2, 750 + $3, 750 = $6, 500 $5, 250 = $6, 500 – $1, 250 $2, 750 7 -9

Toting Up §At the end of his adventure, our investor has three ways of computing his gains and losses: 1. Sum of daily gains and losses. – $7, 500 = $1, 250 – $3, 750 – $1, 250 – $2, 500 2. Contract size times the difference between initial contract price and last settlement price. – $7, 500 = ($1. 24/€ – $1. 30/€) × € 125, 000 – Ending balance on the account minus beginning balance on the account, adjusted for deposits or withdrawals. – $7, 500 = $2, 750 – ($6, 500 + $3, 750) 7 -10

Currency Futures Markets § The CME Group (formerly Chicago Mercantile Exchange) is by far the largest currency futures market. § CME hours are 7: 20 a. m. to 2: 00 p. m. CST Monday-Friday. § Extended-hours trading takes place Sunday through Thursday (local) on GLOBEX i. e. from 5: 00 p. m. to 4: 00 p. m. CST the next day. § The Singapore Exchange offers interchangeable contracts. § There are other markets, but none are close to CME and SIMEX trading volume. § Expiry cycle: March, June, September, December. § The delivery date is the third Wednesday of delivery month. § The last trading day is the second business day preceding the 7 -11 delivery day.

Reading Currency Futures Quotes OPEN HIGH LOW SETTLE OPEN CHG INTEREST Euro/US Dollar (CME)—€ 125, 000; $ per € Mar Jun 1. 4748 1. 4737 1. 4830 1. 4818 1. 4700 1. 4693 1. 4777 1. 4763 . 0028. 0025 172, 396 2, 266 Open interest refers to the number of contracts outstanding for a particular delivery month—it’s a good proxy for demand for a contract. Notice that open interest is greatest in the nearby contract. In general, open interest typically decreases with term to maturity of most futures contracts. 7 -12

Options Contracts: Preliminaries § An option gives the holder the right, but not the obligation, to buy or sell a given quantity of an asset in the future at prices agreed upon today. § Calls vs. Puts: – Call options give the holder the right, but not the obligation, to buy a given quantity of some asset at some time in the future at prices agreed upon today. – Put options give the holder the right, but not the obligation, to sell a given quantity of some asset at some time in the future at prices agreed upon today. 7 -13

Options Contracts: Preliminaries § European versus American options: – European options can only be exercised on the expiration date while American options can be exercised at any time up to and including the expiration date. – American options are usually worth more than European options, other things equal. § Moneyness – If immediate exercise is profitable, an option is “in the money. ” – Out of the money options can still have value. 7 -14

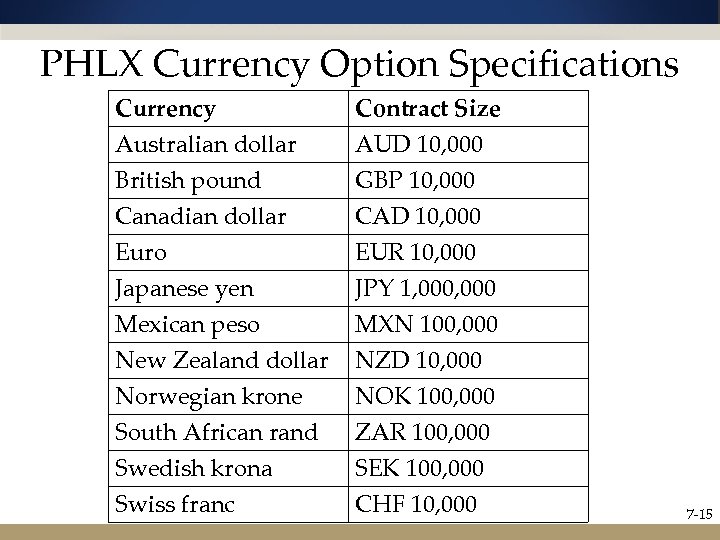PHLX Currency Option Specifications Currency Australian dollar British pound Canadian dollar Contract Size AUD 10, 000 GBP 10, 000 CAD 10, 000 Euro Japanese yen Mexican peso New Zealand dollar Norwegian krone South African rand Swedish krona Swiss franc EUR 10, 000 JPY 1, 000 MXN 100, 000 NZD 10, 000 NOK 100, 000 ZAR 100, 000 SEK 100, 000 CHF 10, 000 7 -15

Basic Option Pricing Relationships at Expiry § At expiry, an American option is worth the same as a European option with the same characteristics. § If the call is in-the-money, it is worth ST – E. § If the call is out-of-the-money, it is worthless. Ca. T = Ce. T = Max[ST – E, 0] § If the put is in-the-money, it is worth E – ST. § If the put is out-of-the-money, it is worthless. Pa. T = Pe. T = Max[E – ST, 0] 7 -16

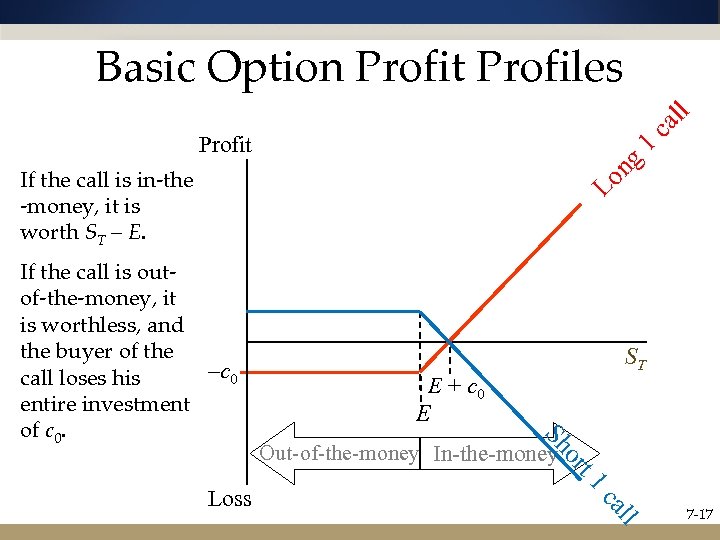ca l l Basic Option Profit Profiles ng 1 Profit Lo If the call is in-the -money, it is worth ST – E. ST E + c 0 E Sh If the call is outof-the-money, it is worthless, and the buyer of the –c 0 call loses his entire investment of c 0. or Out-of-the-money In-the-money t 1 ll ca Loss 7 -17

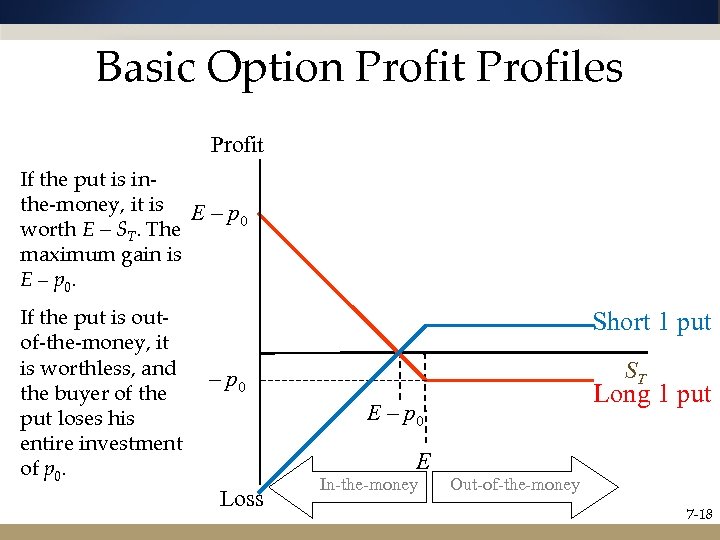Basic Option Profit Profiles Profit If the put is inthe-money, it is E – p 0 worth E – ST. The maximum gain is E – p 0. If the put is outof-the-money, it is worthless, and the buyer of the put loses his entire investment of p 0. Short 1 put ST – p 0 Long 1 put E – p 0 E Loss In-the-money Out-of-the-money 7 -18

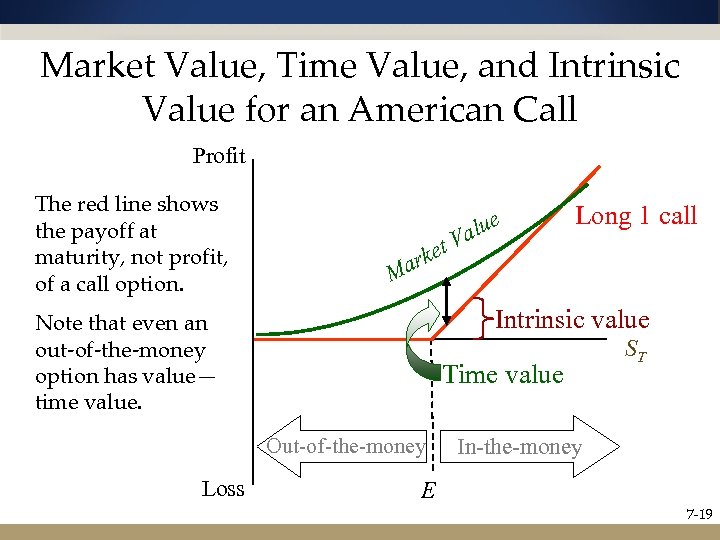Market Value, Time Value, and Intrinsic Value for an American Call Profit The red line shows the payoff at maturity, not profit, of a call option. t rke a V Long 1 call M Intrinsic value Note that even an out-of-the-money option has value— time value. Time value Out-of-the-money Loss e alu ST In-the-money E 7 -19

European Option Pricing Relationships Consider two investments: 1 Buy a European call option on the British pound futures contract. The cash flow today is –Ce. 2 Replicate the upside payoff of the call by: § Borrowing the present value of the dollar, exercise price of the call in the U. S. at i$ , the cash flow today is E (1 + i$) § Lending the present value of ST at i£, the cash flow today is – ST (1 + i£) 7 -20

European Option Pricing Relationships § When the option is in-the-money, both strategies have the same payoff. § When the option is out-of-the-money, it has a higher payoff than the borrowing and lending strategy. ST E § Thus, – , 0 C > Max e (1 + i£) (1 + i$) § Using a similar portfolio to replicate the upside potential of a put, we can show that: ST E Pe > Max (1 + i ) – (1 + i ) , 0 $ £ 7 -21

Binomial Option Pricing Model - Imagine a world where the spot exchange rate is S 0($/€) = $1. 50/€ today and in the next year S 1($/€) is either $1. 80/€ or $1. 20/€. - € 10, 000 will change from $15, 000 to either $18, 000 or $12, 000. - A call option on € 10, 000 with strike price S 0($/€) = $1. 50 will payoff either $3, 000 or zero. - If S 1($/€) = $1. 800/€ the option is in-the-money since you can buy € 10, 000 (worth $18, 000 at S 1($/€) = $1. 80/€ ) for only $15, 000 $18, 000 = € 10, 000 × $1. 80 € 1. 00 up = $3, 000 C 1 $12, 000 = € 10, 000 × $1. 20 € 1. 00 C 1 down = $0 7 -22

Binomial Option Pricing Model We can replicate the payoffs of the call option by taking a long position in a bond with FV = € 5, 000 along with the right amount of dollar-denominated borrowing (in this case borrow the PV of $6, 000). The portfolio payoff in one period matches the option payoffs: $ value of bond FV = € 5, 000 pay debt portfolio C 1($/€) $9, 000 – $6, 000 = $3, 000 $15, 000 $6, 000 – $6, 000 = $0 $0 7 -23

Binomial Option Pricing Model The replicating portfolio’s dollar cost today is the sum of today’s dollar cost of the present value of € 5, 000 less the cash inflow from borrowing the present value of $6, 000: € 5, 000 $1. 50 $6, 000 × – (1 + i€ ) € 1. 00 (1 + i$) When S 0($/€) = $1. 50/€, i$ = 7. 1%, and i€ = 5%, the most a willing buyer should pay for the call option is $1, 540. 62. That’s what it would cost him today to build a portfolio that perfectly replicates the call option payoffs—why pay more to buy a ready-made option? $1, 540. 62 = $7, 142. 86 − $5, 602. 24 7 -24

The Hedge Ratio § We replicated the payoffs of the call option with a levered position in the underlying asset (in this case, borrowing $5, 602. 24 to buy € 4, 761. 90 at the spot). The hedge ratio of a option is the ratio of change in the price of the option to the change in the price of the underlying asset: C up– C down H = up down S 1 – S 1 This ratio gives the number of units of the underlying asset we should hold and the amount of borrowing in order to create a replicating portfolio. 7 -25

Hedge Ratio § This practice of constructing a riskless hedge is sometimes called delta hedging. § The hedge ratio of a call option is positive. – Recall from the example: 1 $3, 000 – $0 C up– C down = H = up down = 2 S 1 – S 1 $18, 000 – $12, 000 The hedge ratio of a put option is negative. These hedge ratios change through time. 7 -26

Currency Futures Options § Currency futures options are options on a currency futures contract. § Exercise of a currency futures option results in a long futures position for the holder of a call or the writer of a put. § Exercise of a currency futures option results in a short futures position for the seller of a call or the buyer of a put. § If the futures position is not offset prior to its expiration, foreign currency will change hands. 7 -27

Binomial Futures Option Pricing A 1 -period at-the-money call option on euro futures has a strike price of F 1($|€) = $1. 5300/€ $1. 80× 1. 071 $1. 8360 = F 1($|€) = € 1. 00× 1. 05 € 1. 00 $1. 50× 1. 071 =$1. 5300 F 1($|€) = € 1. 00× 1. 05 € 1. 00 Option Price = ? Call Option Payoff = $0. 3060 $1. 20× 1. 071 $1. 2240 = F 1($|€) = € 1. 00× 1. 05 € 1. 00 Option Payoff = $0 When a call futures option is exercised the holder acquires: 1. A long position in the futures contract. 2. A cash amount equal to the excess of the futures price over the strike price. 7 -28

Binomial Futures Option Pricing Consider the portfolio: Long H futures contracts Short 1 futures call option $1. 50× 1. 071 = $1. 5300 F 1($|€) = € 1. 00× 1. 05 € 1. 00 $1. 80× 1. 071 $1. 8360 = F 1($|€) = € 1. 00× 1. 05 € 1. 00 Futures Call Payoff = –$0. 3060 Futures Payoff = H × $0. 2700 Portfolio Cash Flow = H × $0. 2700 – $0. 3060 Option Price = $0. 1714 Portfolio is riskless when the portfolio payoffs in the “up” state $1. 20× 1. 071 $1. 2240 equal the payoffs in the “down” = F 1($|€) = state: € 1. 00× 1. 05 € 1. 00 H×$0. 2700 – $0. 3060 = –H×$0. 3300 Futures Payoff = –H × $0. 3300 The “right” amount of futures Option Payoff = $0 contracts is H = 0. 510000. Portfolio Cash Flow = –H × $0. 3300

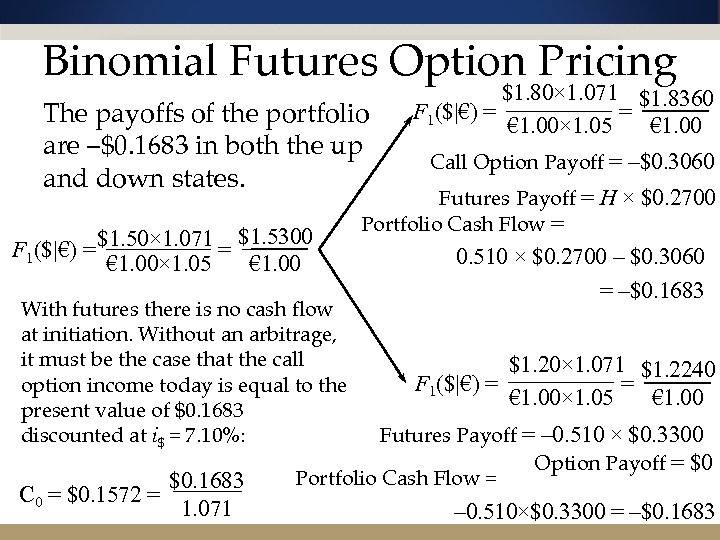Binomial Futures Option Pricing The payoffs of the portfolio are –$0. 1683 in both the up and down states. $1. 50× 1. 071 = $1. 5300 F 1($|€) = € 1. 00× 1. 05 € 1. 00 With futures there is no cash flow at initiation. Without an arbitrage, it must be the case that the call option income today is equal to the present value of $0. 1683 discounted at i$ = 7. 10%: $0. 1683 C 0 = $0. 1572 = 1. 071 $1. 80× 1. 071 $1. 8360 = F 1($|€) = € 1. 00× 1. 05 € 1. 00 Call Option Payoff = –$0. 3060 Futures Payoff = H × $0. 2700 Portfolio Cash Flow = 0. 510 × $0. 2700 – $0. 3060 = –$0. 1683 $1. 20× 1. 071 $1. 2240 = F 1($|€) = € 1. 00× 1. 05 € 1. 00 Futures Payoff = – 0. 510 × $0. 3300 Option Payoff = $0 Portfolio Cash Flow = – 0. 510×$0. 3300 = –$0. 1683

Risk Neutral Valuation of Options § Calculating the hedge ratio is vitally important if you are going to use options. – The seller needs to know the hedge ratio if he wants to protect his profits or eliminate his downside risk. – The buyer needs to know the hedge ratio to decide how many options to buy. § Knowing what the hedge ratio is isn’t especially important if you are only trying to value options. § Risk Neutral Valuation is a very handy shortcut to valuation. 7 -31

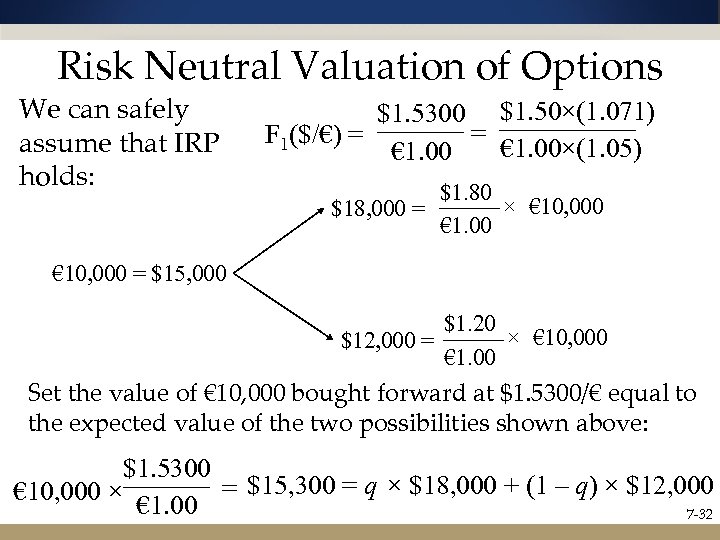Risk Neutral Valuation of Options We can safely assume that IRP holds: $1. 5300 $1. 50×(1. 071) = F 1($/€) = € 1. 00×(1. 05) € 1. 00 $1. 80 × € 10, 000 $18, 000 = € 1. 00 € 10, 000 = $15, 000 $1. 20 × € 10, 000 $12, 000 = € 1. 00 Set the value of € 10, 000 bought forward at $1. 5300/€ equal to the expected value of the two possibilities shown above: $1. 5300 = $15, 300 = q × $18, 000 + (1 – q) × $12, 000 € 10, 000 × € 1. 00 7 -32

Risk Neutral Valuation of Options Solving for q gives the risk-neutral probability of an “up” move in the exchange rate: $15, 300 = q × $18, 000 + (1 – q) × $12, 000 $15, 300 – $12, 000 q= $18, 000 – $12, 000 q = 11/20 = 0. 55000 7 -33

Risk Neutral Valuation of Options 11 /2 0 Now we can value the call option as the present value (discounted at the USD risk-free rate) of the expected value of the option payoffs, calculated using the riskneutral probabilities. C 0 = $1, 540. 62 = 9 / 20 € 10, 000 = $15, 000 $1, 540. 62 $1. 80 × € 10, 000 ←value of € 10, 000 $18, 000 = € 1. 00 $3, 000= payoff of right to buy € 10, 000 for $15, 000 $1. 20 × € 10, 000 ←value of € 10, 000 $12, 000 = € 1. 00 $0 = payoff of right to buy € 10, 000 for $15, 000 (11/20) ×$3, 000 + (9/20)×$0 1. 071 7 -34

Test Your Intuition Use risk neutral valuation to find the value of a put option on $15, 000 with a strike price of € 10, 000. Hint: Given that we just found the value of a call option on € 10, 000 with a strike price of $15, 000 to be $1, 540. 62, this should be easy in the sense that we already know the right answer. $1. 50 As before, i$ = 7. 1%, i€ = 5%, S 0($/€) = € 1. 00 $1. 50× 1. 071 $1. 5300 = F 1($/€) = € 1. 00× 1. 05 € 1. 00 7 -35

Test Your Intuition (continued) $1. 50× 1. 071 $1. 5300 = F 1($/€) = € 1. 00× 1. 05 € 1. 00 € 12, 500 = € 1. 00 × $15, 000 ←€ value of $15, 000 $1. 20 when S = $1. 20/€ 1 € 10, 000 = $15, 000 € 1. 00 ×$15, 000 ←€ value of $15, 000 € 8, 333. 33 = $1. 80 when S 1 = $1. 80/€ € 1. 00 $15, 000 × = € 9, 803. 92 $1. 5300 € 9, 803. 92 = q × € 12, 500 + (1 – q) × € 8, 200 € 9, 803. 92– € 8, 333. 33 q= € 12, 500 – € 8, 333. 33 q = 6/17 7 -36

Test Your Intuition (continued) € 1. 00 × $15, 000 ←value of $15, 000 € 12, 500 = $1. 20 € 0 = payoff of right to sell $15, 000 for € 10, 000 = $15, 000 € 1, 027. 08 €P 0 = € 1, 027. 08 = € 1. 00 × $15, 000 ←value of $15, 000 € 8, 333. 33 = $1. 80 € 1, 666. 67= payoff of right to sell $15, 000 for € 10, 000 6/ × € 0 + (11/17)×€ 1, 666. 67 17 1. 05 $P 0 = $1, 540. 62 = € 1, 027. 08 × $1. 50 € 1. 00 7 -37

Risk Neutral Valuation Practice Use risk neutral valuation to value a PUT option on £ 8, 000 with a strike price of € 10, 000. 9 € 10, 666. 67 90 0 S 0(£/€) = £ 0. 80/€, i£ = 15½% and i€ = 5% up. 4 0 p 1 = € 0 In the next year, there are two possibilities: S 1(£/€) = £ 1. 00/€ or € 10, 000 1 S 1(£/€) = £ 0. 75/€ 0 Step 1: Calculate risk neutral probabilities. . 40 909 € 8, 000 Step 2: Calculate option value as the present value down of the expected value of the option payoffs. p 1 = € 2, 000 € 9, 090. 91 = q × € 10, 666. 67+ (1 – q) × € 8, 000 € 9, 090. 91– € 8, 000 q = € 10, 666. 67– € 8, 000 = 9/22 p 0 = € 1, 125. 54= 13/ 22 x € 2, 000 1. 05 7 -38

Black–Scholes Pricing Formulae The Black-Scholes formulae for the price of a European call and a put written on currency are: N(d) = Probability that a standardized, normally distributed, random variable will be less than or equal to d. 7 -39

Black–Scholes Pricing Formula § Use the European option pricing formula to find the value of a six-month call option on Japanese yen. § The strike price is $1 = ¥ 100. The volatility is 25 percent per annum; r$ = 5. 5% and r¥ = 6%.