737803c0dc9c785f8068961cda2acc0e.ppt
- Количество слайдов: 72
 Future Directions in Computer Science John Hopcroft Cornell University Ithaca, New York
Future Directions in Computer Science John Hopcroft Cornell University Ithaca, New York
 Time of change n There is a fundamental revolution taking place that is changing all aspects of our lives. n Those individuals who recognize this and position themselves for the future will benefit enormously.
Time of change n There is a fundamental revolution taking place that is changing all aspects of our lives. n Those individuals who recognize this and position themselves for the future will benefit enormously.
 Drivers of change in Computer Science Computers are becoming ubiquitous n Speed sufficient for word processing, email, chat and spreadsheets n Merging of computing and communications n Data available in digital form n Devices being networked n
Drivers of change in Computer Science Computers are becoming ubiquitous n Speed sufficient for word processing, email, chat and spreadsheets n Merging of computing and communications n Data available in digital form n Devices being networked n
 Computer Science departments are beginning to develop courses that cover underlying theory for Random graphs n Phase transitions n Giant components n Spectral analysis n Small world phenomena n Grown graphs n
Computer Science departments are beginning to develop courses that cover underlying theory for Random graphs n Phase transitions n Giant components n Spectral analysis n Small world phenomena n Grown graphs n
 What is theory needed to support the future? Search n Networks and sensors n Large amounts of noisy, high dimensional data n Integration of systems and sources of information n
What is theory needed to support the future? Search n Networks and sensors n Large amounts of noisy, high dimensional data n Integration of systems and sources of information n
 Internet queries are changing Today n Autos n Graph Tomorrow n theory n Colleges, universities n Computer science n n n Which car should I buy? Construct an annotated bibliography on graph theory Where should I go to college? How did the field of CS develop?
Internet queries are changing Today n Autos n Graph Tomorrow n theory n Colleges, universities n Computer science n n n Which car should I buy? Construct an annotated bibliography on graph theory Where should I go to college? How did the field of CS develop?
 What car should I buy? n List of makes ¨ Cost ¨ Reliability ¨ Fuel economy ¨ Crash safety n Pertinent articles ¨ Consumer reports ¨ Car and driver
What car should I buy? n List of makes ¨ Cost ¨ Reliability ¨ Fuel economy ¨ Crash safety n Pertinent articles ¨ Consumer reports ¨ Car and driver
 Where should I go to college? n List of factors that might influence choice ¨ Cost ¨ Geographic location ¨ Size ¨ Type n of institution Metrics ¨ Ranking of programs ¨ Student faculty ratios ¨ Graduates from your high school/neighborhood
Where should I go to college? n List of factors that might influence choice ¨ Cost ¨ Geographic location ¨ Size ¨ Type n of institution Metrics ¨ Ranking of programs ¨ Student faculty ratios ¨ Graduates from your high school/neighborhood
 How did field develop? n n From ISI database create set of important papers in field? Extract important authors n author of key paper n author of several important papers n thesis advisor of Ph. D. ’s student(s) who is (are) important author(s) Extract key institutions n institution of important author(s) n Ph. D. granting institution of important authors Output n Directed graph of key papers n Flow of Ph. D. ’s geographically with time n Flow of ideas
How did field develop? n n From ISI database create set of important papers in field? Extract important authors n author of key paper n author of several important papers n thesis advisor of Ph. D. ’s student(s) who is (are) important author(s) Extract key institutions n institution of important author(s) n Ph. D. granting institution of important authors Output n Directed graph of key papers n Flow of Ph. D. ’s geographically with time n Flow of ideas


 Theory to support new directions Large graphs n Spectral analysis n High dimensions and dimension reduction n Clustering n Collaborative filtering n Extracting signal from noise n
Theory to support new directions Large graphs n Spectral analysis n High dimensions and dimension reduction n Clustering n Collaborative filtering n Extracting signal from noise n
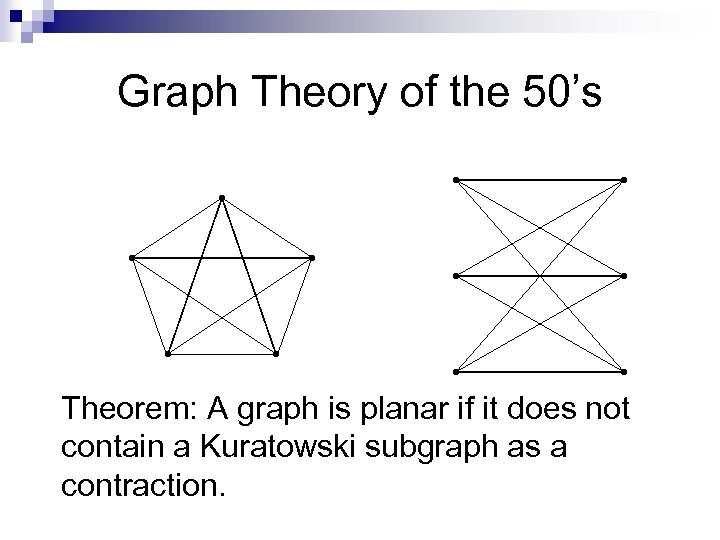 Graph Theory of the 50’s Theorem: A graph is planar if it does not contain a Kuratowski subgraph as a contraction.
Graph Theory of the 50’s Theorem: A graph is planar if it does not contain a Kuratowski subgraph as a contraction.
 Theory of Large Graphs Large graphs n Billion vertices n Exact edges present not critical Theoretical basis for study of large graphs n Maybe theory of graph generation n Invariant to small changes in definition n Must be able to prove basic theorems
Theory of Large Graphs Large graphs n Billion vertices n Exact edges present not critical Theoretical basis for study of large graphs n Maybe theory of graph generation n Invariant to small changes in definition n Must be able to prove basic theorems
 Erdös-Renyi n vertices n each of n 2 potential edges is present with independent probability n N pn (1 -p)N-n n number of vertices vertex degree binomial degree distribution
Erdös-Renyi n vertices n each of n 2 potential edges is present with independent probability n N pn (1 -p)N-n n number of vertices vertex degree binomial degree distribution
 Generative models for graphs Vertices and edges added at each unit of time n Rule to determine where to place edges n ¨ Uniform probability ¨ Preferential attachment - gives rise to power law degree distributions
Generative models for graphs Vertices and edges added at each unit of time n Rule to determine where to place edges n ¨ Uniform probability ¨ Preferential attachment - gives rise to power law degree distributions
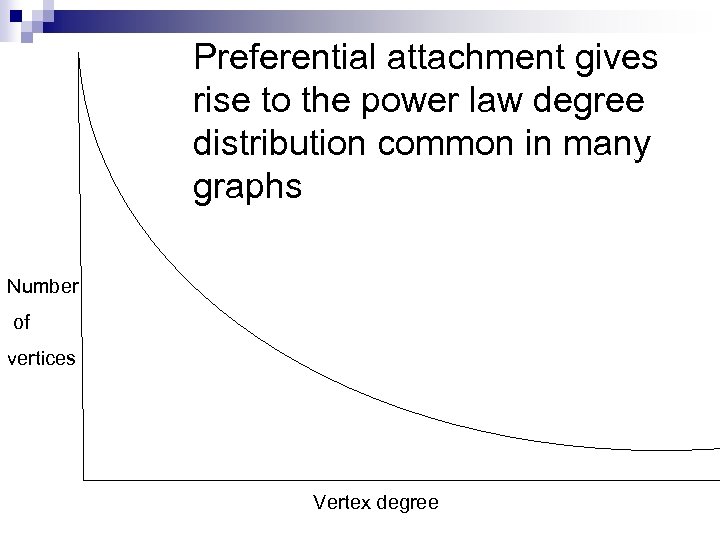 Preferential attachment gives rise to the power law degree distribution common in many graphs Number of vertices Vertex degree
Preferential attachment gives rise to the power law degree distribution common in many graphs Number of vertices Vertex degree
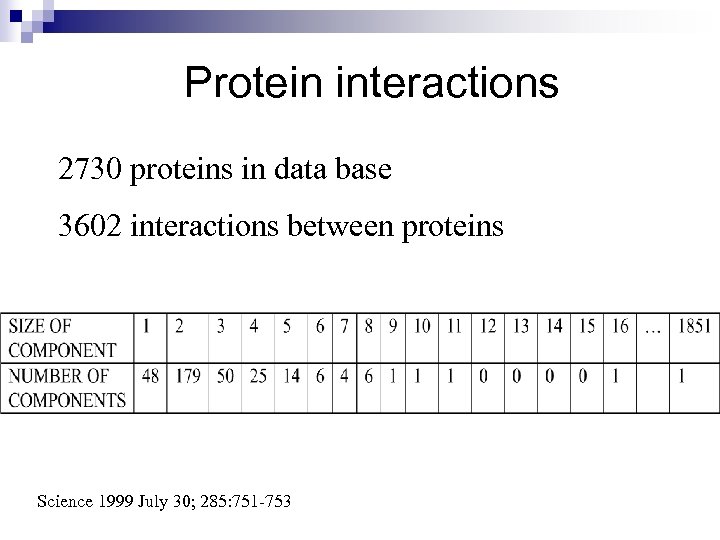 Protein interactions 2730 proteins in data base 3602 interactions between proteins Science 1999 July 30; 285: 751 -753
Protein interactions 2730 proteins in data base 3602 interactions between proteins Science 1999 July 30; 285: 751 -753
 Giant Component 1. Create n isolated vertices 2. Add Edges randomly one by one 3. Compute number of connected components
Giant Component 1. Create n isolated vertices 2. Add Edges randomly one by one 3. Compute number of connected components
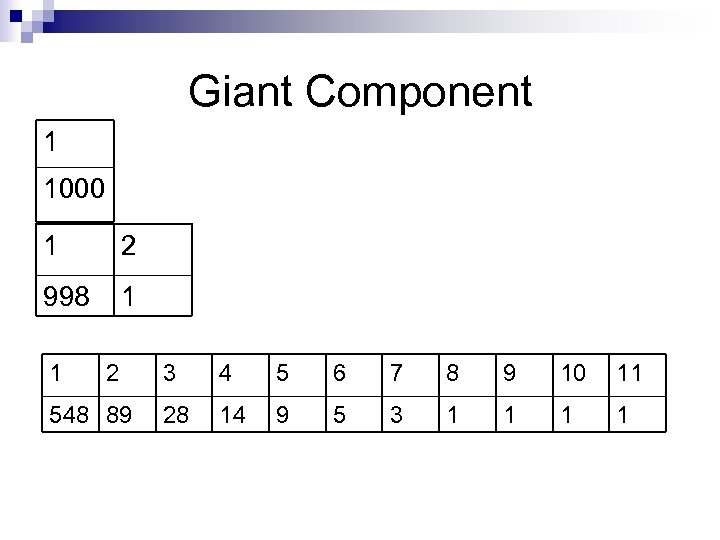 Giant Component 1 1000 1 2 998 1 1 2 548 89 3 4 5 6 7 8 9 10 11 28 14 9 5 3 1 1
Giant Component 1 1000 1 2 998 1 1 2 548 89 3 4 5 6 7 8 9 10 11 28 14 9 5 3 1 1
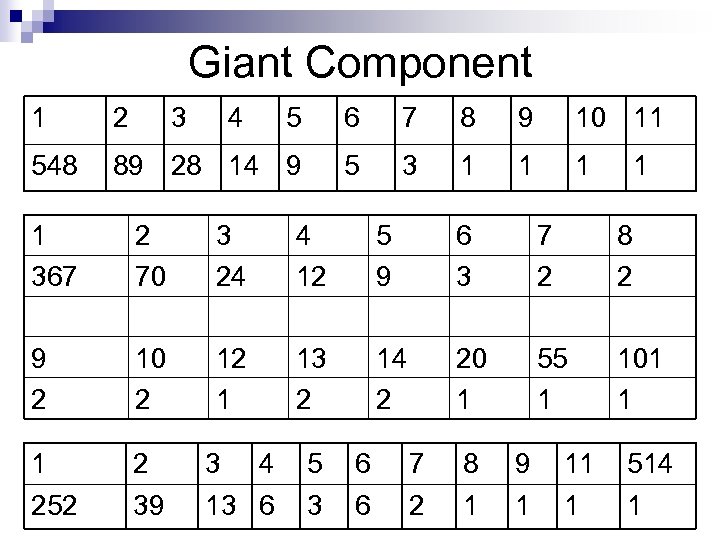 Giant Component 1 2 3 4 5 6 7 8 9 10 11 548 89 28 14 9 5 3 1 1 1 367 2 70 3 24 4 12 5 9 6 3 7 2 8 2 9 2 10 2 12 1 13 2 14 2 20 1 55 1 101 1 1 252 2 39 3 4 13 6 5 3 6 6 7 2 8 1 9 1 11 1 514 1
Giant Component 1 2 3 4 5 6 7 8 9 10 11 548 89 28 14 9 5 3 1 1 1 367 2 70 3 24 4 12 5 9 6 3 7 2 8 2 9 2 10 2 12 1 13 2 14 2 20 1 55 1 101 1 1 252 2 39 3 4 13 6 5 3 6 6 7 2 8 1 9 1 11 1 514 1
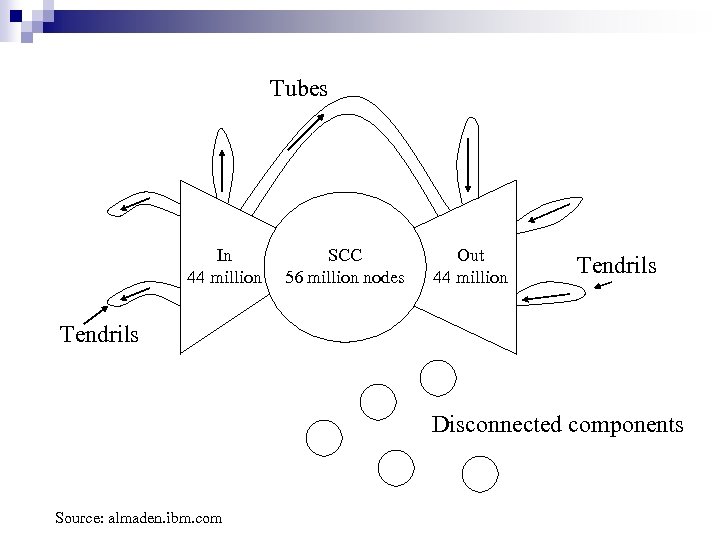 Tubes In 44 million SCC 56 million nodes Out 44 million Tendrils Disconnected components Source: almaden. ibm. com
Tubes In 44 million SCC 56 million nodes Out 44 million Tendrils Disconnected components Source: almaden. ibm. com
 n G(n, p) Phase transitions ¨ Emergence of cycle ¨ Giant component ¨ Connected graph n N(p) ¨ Emergence n of arithmetic sequence CNF satisfiability ¨ Fix number of variables, increase number of clauses
n G(n, p) Phase transitions ¨ Emergence of cycle ¨ Giant component ¨ Connected graph n N(p) ¨ Emergence n of arithmetic sequence CNF satisfiability ¨ Fix number of variables, increase number of clauses
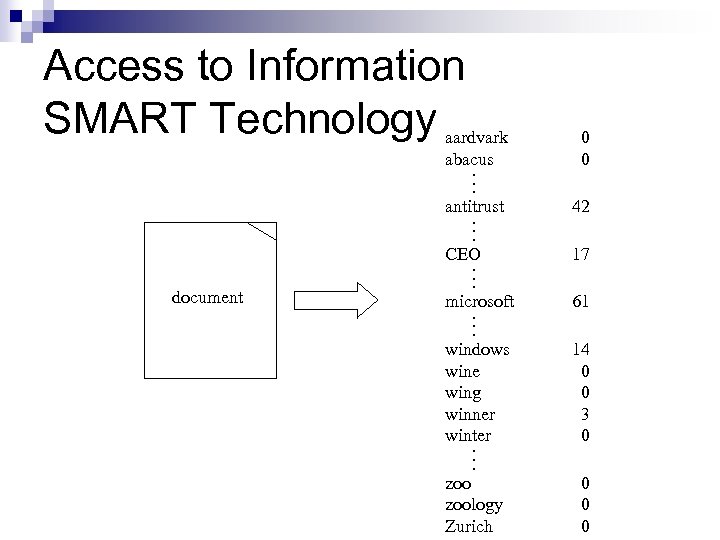 Access to Information SMART Technology aardvark abacus. . . 0 0 antitrust. . . document 42 microsoft. . . 61 CEO. . . 17 windows wine wing winner winter. . . 14 0 0 3 0 zoology Zurich 0 0 0
Access to Information SMART Technology aardvark abacus. . . 0 0 antitrust. . . document 42 microsoft. . . 61 CEO. . . 17 windows wine wing winner winter. . . 14 0 0 3 0 zoology Zurich 0 0 0
 Locating relevant documents Query: Where can I get information on gates? 2, 060, 000 hits Bill Gates 593, 000 Gates county 177, 000 baby gates 170, 000 gates of heaven 169, 000 automatic gates 83, 000 fences and gates 43, 000 Boolean gates 19, 000
Locating relevant documents Query: Where can I get information on gates? 2, 060, 000 hits Bill Gates 593, 000 Gates county 177, 000 baby gates 170, 000 gates of heaven 169, 000 automatic gates 83, 000 fences and gates 43, 000 Boolean gates 19, 000
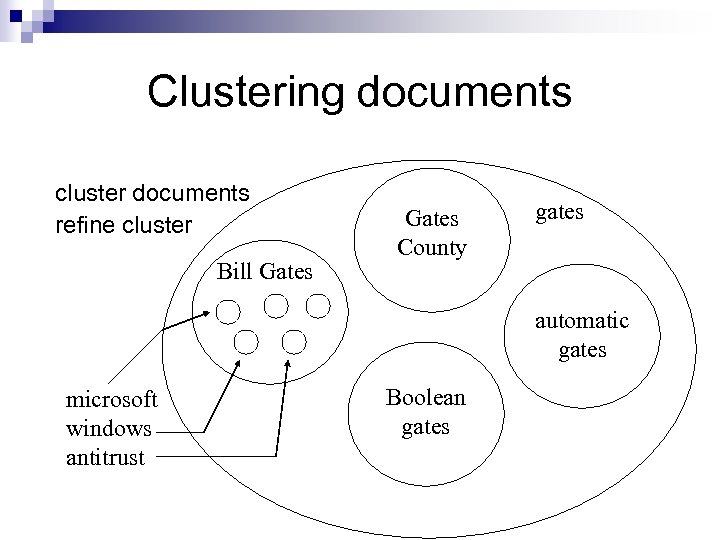 Clustering documents cluster documents refine cluster Bill Gates County gates automatic gates microsoft windows antitrust Boolean gates
Clustering documents cluster documents refine cluster Bill Gates County gates automatic gates microsoft windows antitrust Boolean gates
 Refinement of another type: books s tic a em m ath r ist ics s hy p y m he c children’s books textbooks reference books general population y n om a o str
Refinement of another type: books s tic a em m ath r ist ics s hy p y m he c children’s books textbooks reference books general population y n om a o str
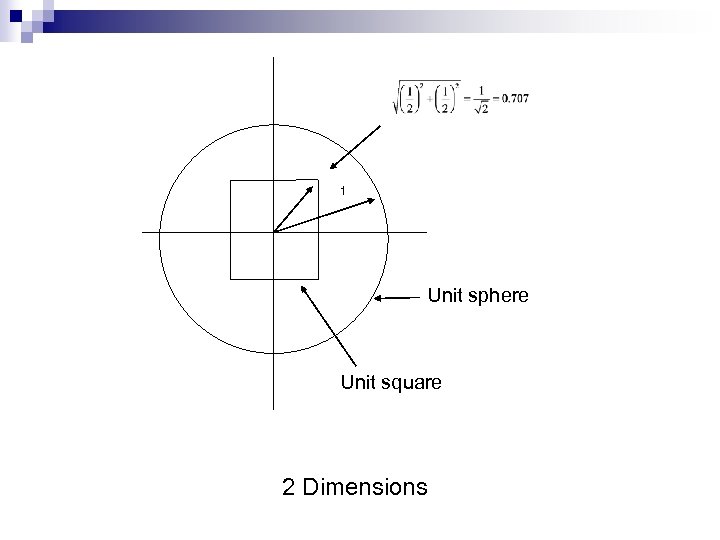
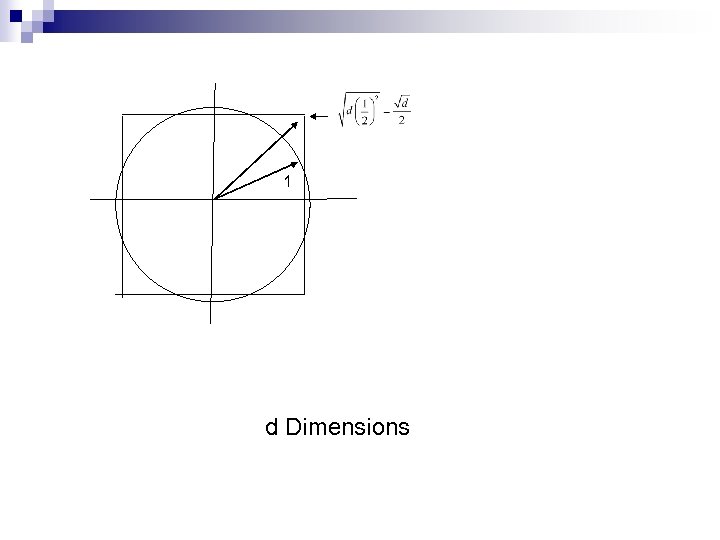
 High Dimensions Intuition from two and three dimensions not valid for high dimension Volume of cube is one in all dimensions Volume of sphere goes to zero
High Dimensions Intuition from two and three dimensions not valid for high dimension Volume of cube is one in all dimensions Volume of sphere goes to zero
 1 Unit sphere Unit square 2 Dimensions
1 Unit sphere Unit square 2 Dimensions
 4 Dimensions
4 Dimensions
 1 d Dimensions
1 d Dimensions
 Almost all area of the unit cube is outside the unit sphere
Almost all area of the unit cube is outside the unit sphere
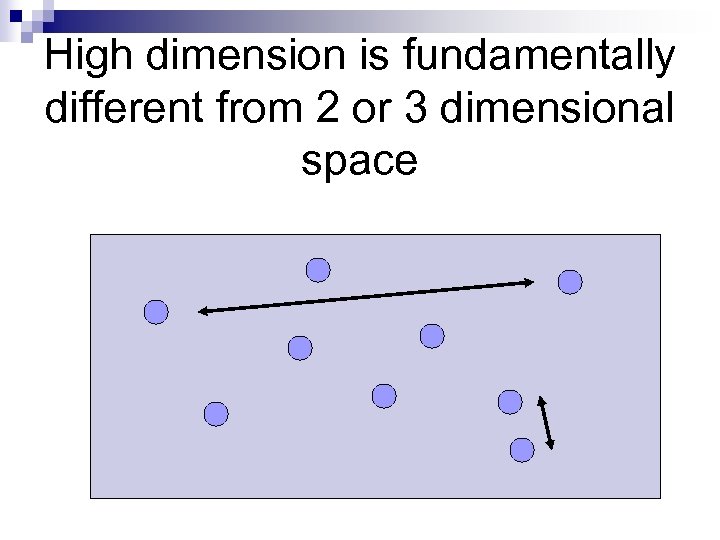 High dimension is fundamentally different from 2 or 3 dimensional space
High dimension is fundamentally different from 2 or 3 dimensional space
 High dimensional data is inherently unstable n n Given n random points in d dimensional space essentially all n 2 distances are equal.
High dimensional data is inherently unstable n n Given n random points in d dimensional space essentially all n 2 distances are equal.
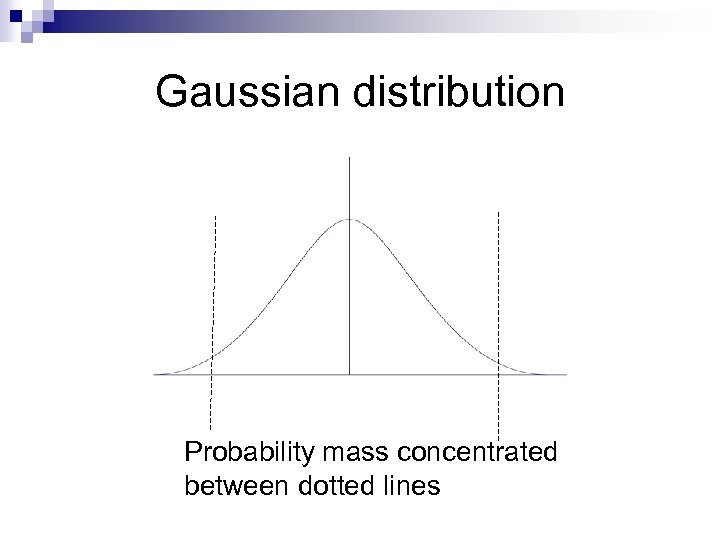 Gaussian distribution Probability mass concentrated between dotted lines
Gaussian distribution Probability mass concentrated between dotted lines
 Gaussian in high dimensions
Gaussian in high dimensions
 Two Gaussians
Two Gaussians
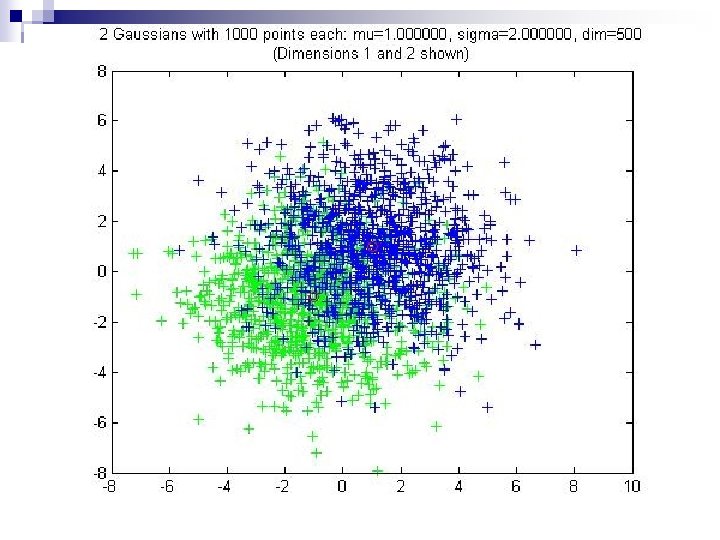
 Distance between two random points from same Gaussian n Points on thin annulus of radius n Approximate by sphere of radius n Average distance between two points is (Place one pt at N. Pole other at random. Almost surely second point near the equator. )
Distance between two random points from same Gaussian n Points on thin annulus of radius n Approximate by sphere of radius n Average distance between two points is (Place one pt at N. Pole other at random. Almost surely second point near the equator. )
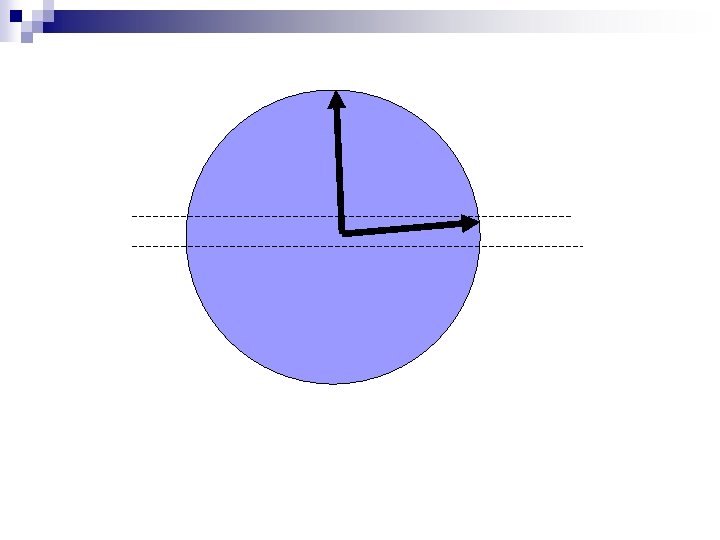
 Expected distance between pts from two Gaussians separated by δ Rotate axis so first point is perpendicular to screen All other points close to plane of screen
Expected distance between pts from two Gaussians separated by δ Rotate axis so first point is perpendicular to screen All other points close to plane of screen
 Expected distance between pts from two Gaussians separated by δ
Expected distance between pts from two Gaussians separated by δ
 Expected distance between pts from two Gaussians separated by δ
Expected distance between pts from two Gaussians separated by δ
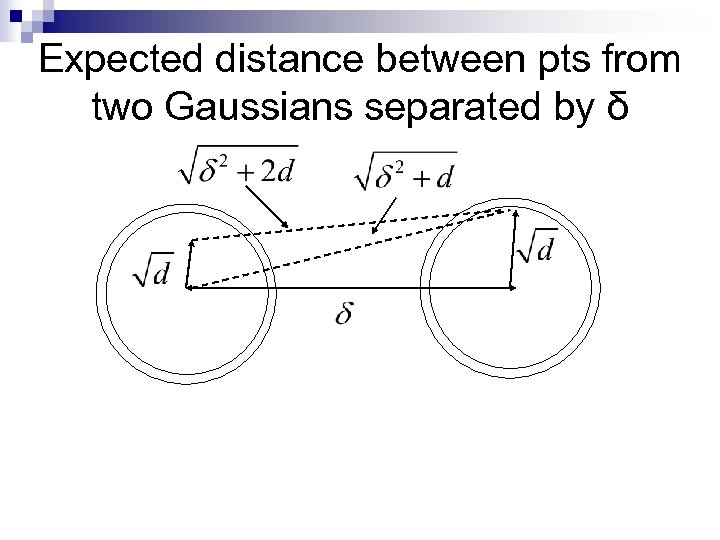 Expected distance between pts from two Gaussians separated by δ
Expected distance between pts from two Gaussians separated by δ
 Can separate points from two Gaussians if
Can separate points from two Gaussians if
 Dimension reduction Project points onto subspace containing centers of Gaussians n Reduce dimension from d to k, the number of Gaussians n
Dimension reduction Project points onto subspace containing centers of Gaussians n Reduce dimension from d to k, the number of Gaussians n
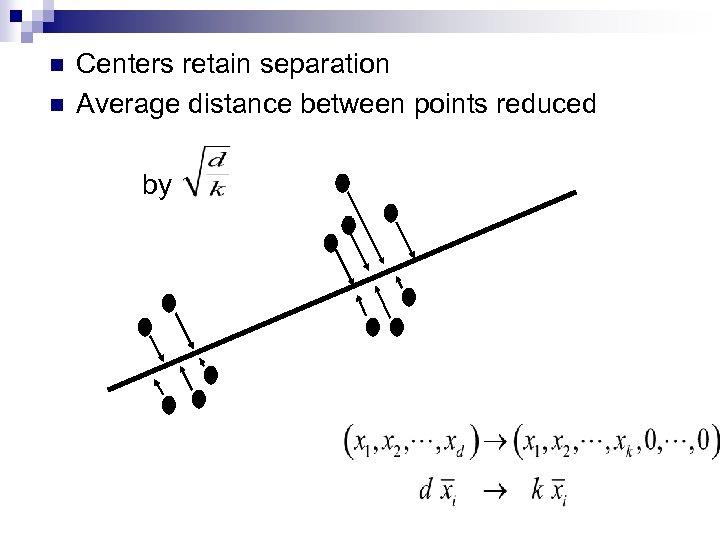 n n Centers retain separation Average distance between points reduced by
n n Centers retain separation Average distance between points reduced by
 Can separate Gaussians provided > some constant involving k and γ independent of the dimension
Can separate Gaussians provided > some constant involving k and γ independent of the dimension
 n Ranking is important ¨ Restaurants ¨ Movies ¨ Web n pages Multi billion dollar industry
n Ranking is important ¨ Restaurants ¨ Movies ¨ Web n pages Multi billion dollar industry
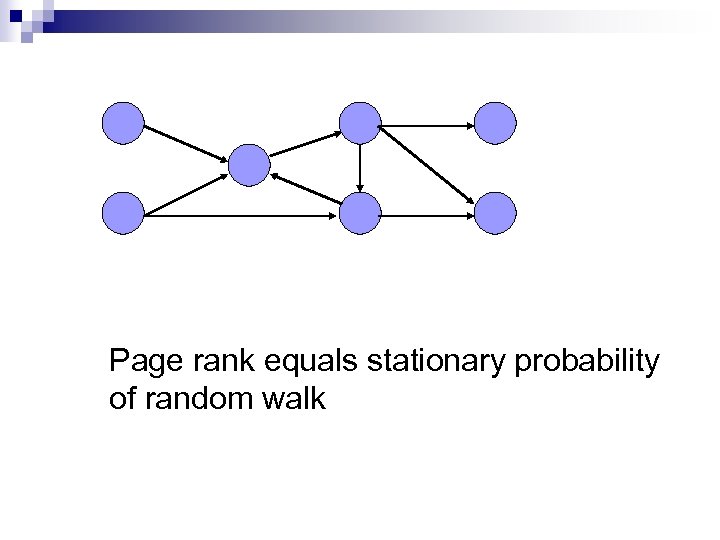 Page rank equals stationary probability of random walk
Page rank equals stationary probability of random walk
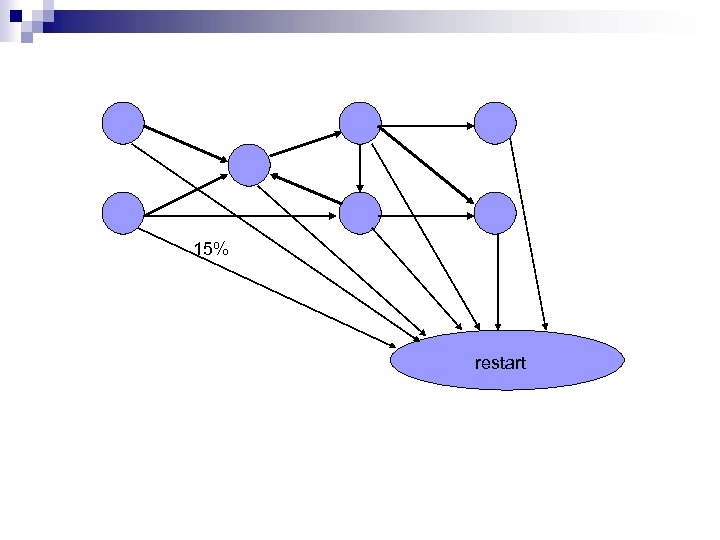 15% restart
15% restart
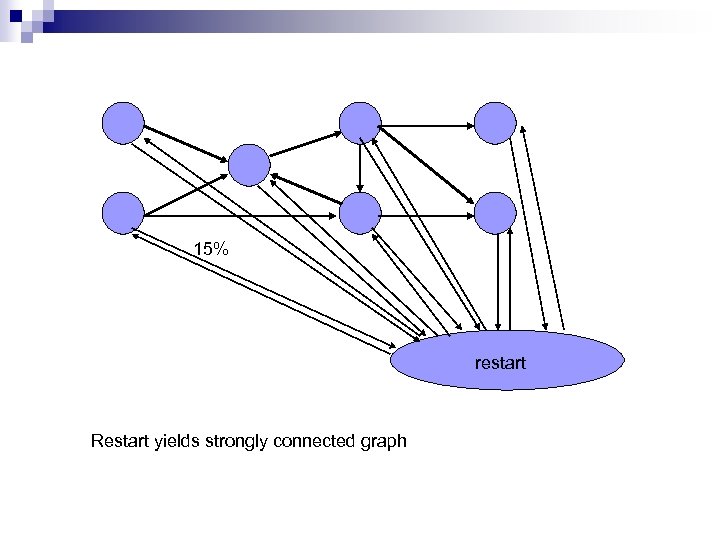 15% restart Restart yields strongly connected graph
15% restart Restart yields strongly connected graph
 Suppose you wish to increase the page rank of vertex v n Capture restart web farm n Capture random walk small cycles
Suppose you wish to increase the page rank of vertex v n Capture restart web farm n Capture random walk small cycles
 Capture restart n Buy 20, 000 url’s and capture restart Can be countered by small restart value n Small restart increases web rank of page that captures random walk by small cycles. n
Capture restart n Buy 20, 000 url’s and capture restart Can be countered by small restart value n Small restart increases web rank of page that captures random walk by small cycles. n
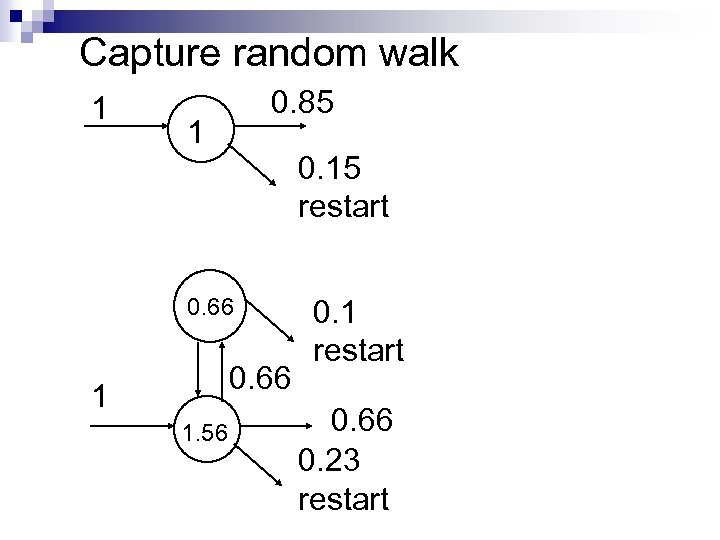 Capture random walk 1 0. 85 1 0. 15 restart 0. 66 1 1. 56 0. 1 restart 0. 66 0. 23 restart
Capture random walk 1 0. 85 1 0. 15 restart 0. 66 1 1. 56 0. 1 restart 0. 66 0. 23 restart
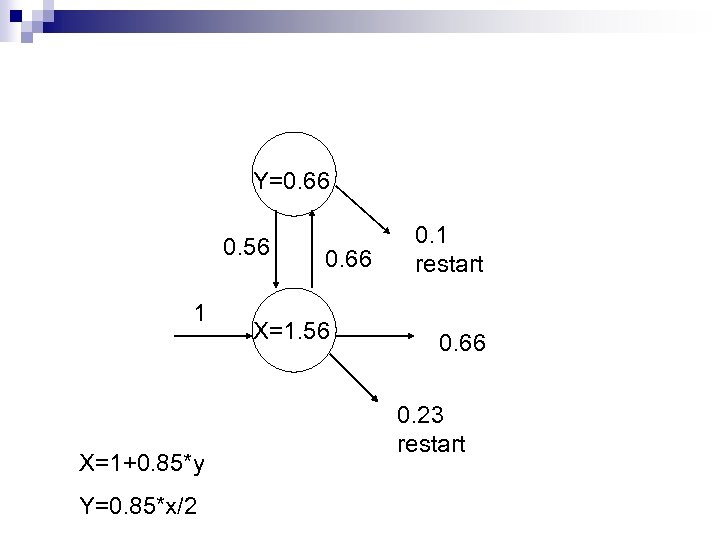 Y=0. 66 0. 56 1 X=1+0. 85*y Y=0. 85*x/2 0. 66 X=1. 56 0. 1 restart 0. 66 0. 23 restart
Y=0. 66 0. 56 1 X=1+0. 85*y Y=0. 85*x/2 0. 66 X=1. 56 0. 1 restart 0. 66 0. 23 restart
 If one loop increases Pagerank from 1 to 1. 56 why not add many self loops? Maximum increase in Pagerank is 6. 67
If one loop increases Pagerank from 1 to 1. 56 why not add many self loops? Maximum increase in Pagerank is 6. 67
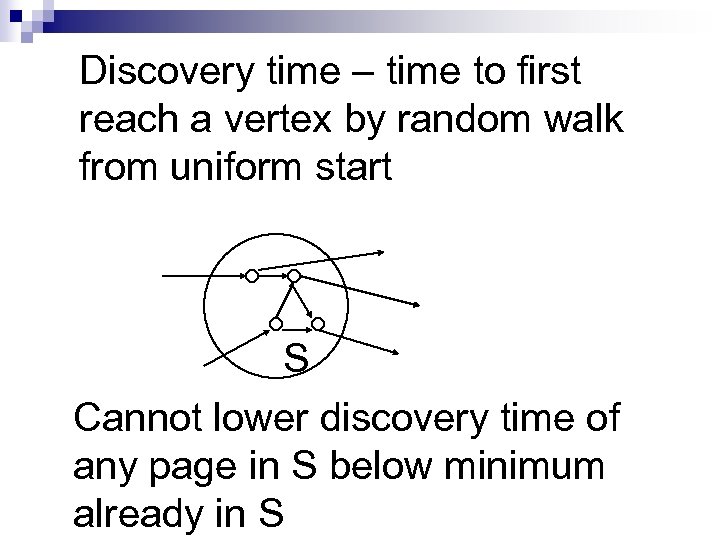 Discovery time – time to first reach a vertex by random walk from uniform start S Cannot lower discovery time of any page in S below minimum already in S
Discovery time – time to first reach a vertex by random walk from uniform start S Cannot lower discovery time of any page in S below minimum already in S
 Why not replace Pagerank by discovery time? No efficient algorithm for discovery time Discovery. Time(v) remove edges out of v calculate Pagerank(v) in modified graph
Why not replace Pagerank by discovery time? No efficient algorithm for discovery time Discovery. Time(v) remove edges out of v calculate Pagerank(v) in modified graph
 n Is there a way for a spammer to raise Pagerank in a way that is not statistically detectable
n Is there a way for a spammer to raise Pagerank in a way that is not statistically detectable
 Information is important n When a customer makes a purchase what else is he likely to buy? n Camera Memory card ¨ Batteries ¨ Carrying case ¨ Etc. ¨ n Knowing what a customer is likely to buy is important information.
Information is important n When a customer makes a purchase what else is he likely to buy? n Camera Memory card ¨ Batteries ¨ Carrying case ¨ Etc. ¨ n Knowing what a customer is likely to buy is important information.
 n How can we extract information from a customer’s visit to a web site? ¨ What web pages were visited? ¨ What order? ¨ How long?
n How can we extract information from a customer’s visit to a web site? ¨ What web pages were visited? ¨ What order? ¨ How long?
 Detecting trends before they become obvious n Is some category of customer changing their buying habits? ¨ Purchases, travel destination, vacations Is there some new trend in the stock market? n How do we detect changes in a large database over time? n
Detecting trends before they become obvious n Is some category of customer changing their buying habits? ¨ Purchases, travel destination, vacations Is there some new trend in the stock market? n How do we detect changes in a large database over time? n
 Identifying Changing Patterns in a Large Data Set How soon can one detect a change in patterns in a large volume of information? n How large must a change be in order to distinguish it from random fluctuations? n
Identifying Changing Patterns in a Large Data Set How soon can one detect a change in patterns in a large volume of information? n How large must a change be in order to distinguish it from random fluctuations? n
 Conclusions We are in an exciting time of change. n Information technology is a big driver of that change. n The computer science theory of the last thirty years needs to be extended to cover the next thirty years. n
Conclusions We are in an exciting time of change. n Information technology is a big driver of that change. n The computer science theory of the last thirty years needs to be extended to cover the next thirty years. n


