Функція y = tg x: графік та властивості.

х у 1 0 Лінія тангенсів Назва «тангенс», походить від латинського tanger

х у Означення функції y = tg x 1 0 α Pα(x;y) y

Графік функції y = tg x Графіком функції y = tg x є

Властивості функції y = tg x х = p /2+ pn, (n Є Z)

2. Область значень: Властивості функції y = tg x

Властивості функції y = tg x Графік функції симетричний відносно початку координат О(0; 0)

У Х Функція y = tg x – періодична з найменшим додатнім періодом T

У Х 5. Точки перетину графіка функції y = tg x з

У Х 6. Проміжки знакосталості: Властивості функції y = tg x

При збільшенні аргументу функції х (x2> x1) ордината відповідної точки лінії тангенсів збільшується,

У Х Властивості функції y = tg x Найбільшого та найменшого значень функція не

Виконання вправ на закріплення властивостей функції у= tg x Вправа 1. Користуючись властивостями функції

Перевір правильність виконання та запис пояснень до вправ: Вправа 1 Розв’язання Оскільки tg 1400=

Виконай самостійно: Вправа 1. Користуючись властивостями функції у= tg x, порівняйте числа:

Побудувати графік функції y = - tg x Для побудови графіка функції y

Побудувати графік функції y = tg x + 1 Для побудови графіка функції

Побудувати графік функції y = tg (x + p/6) Для побудови графіка функції

У Х Побудувати графік функції y = Іtg xІ Для побудови графіка функції

У Х Побудувати графік функції y = tg | x | Для побудови

Перевір себе! Серед наведених графіків зазначте графік функції y=|tg x| А Б В Г

Перевір себе! 1. Функція y=2tg x зростає на проміжку: 2. Графік функція y =

Скачать презентацию Функція y = tg x: графік та властивості.

13220-tg.ppt

Количество слайдов: 25

>Функція y = tg x: графік та властивості. Функція y = tg x: графік та властивості.

>х у 1 0 Лінія тангенсів Назва «тангенс», походить від латинського tanger х у 1 0 Лінія тангенсів Назва «тангенс», походить від латинського tanger (дотикатись). Оскільки пряма ОР проходить через початок координат, то її рівняння у=kx. Але ця пряма проходить через точку Р з координатами (cosa;sina), отже, координати точки Р задовільняють рівняння прямої у=кх, тобто sina=kcosa. Звідси k=sina/cosa=tga. Таким чином, пряма ОР має рівняння y=(tga)x. Отже, тангенс кута(числа) а-це ордината відповідної точки на лінії тангенсів А(1;у) Р

>х у Означення функції y = tg x 1 0 α Pα(x;y) y х у Означення функції y = tg x 1 0 α Pα(x;y) y x Тангенсом кута називають відношення ординати точки Pα(x;y) до її абсциси.

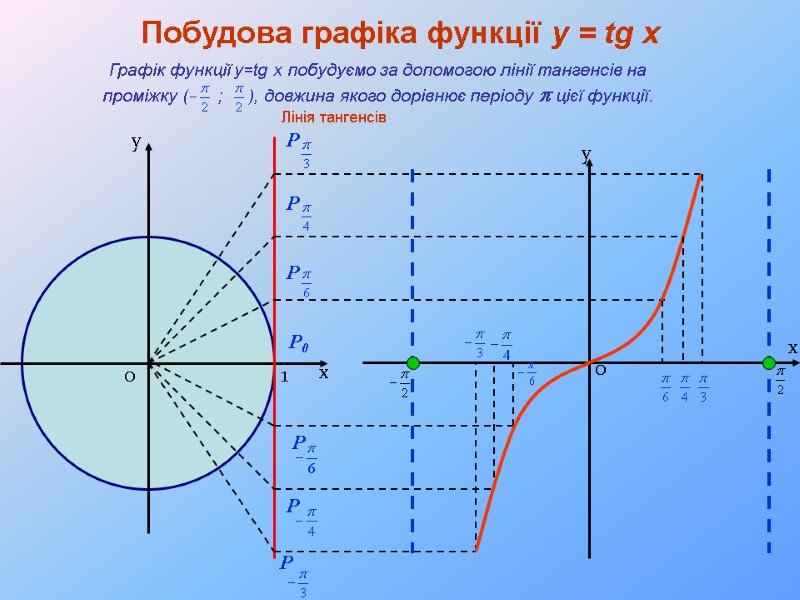
>х у 1 0 Лінія тангенсів х 0 у P0 P P х у 1 0 Лінія тангенсів х 0 у P0 P P P P P P Побудова графіка функції y = tg x Графік функції y=tg x побудуємо за допомогою лінії тангенсів на проміжку ( ; ), довжина якого дорівнює періоду p цієї функції.

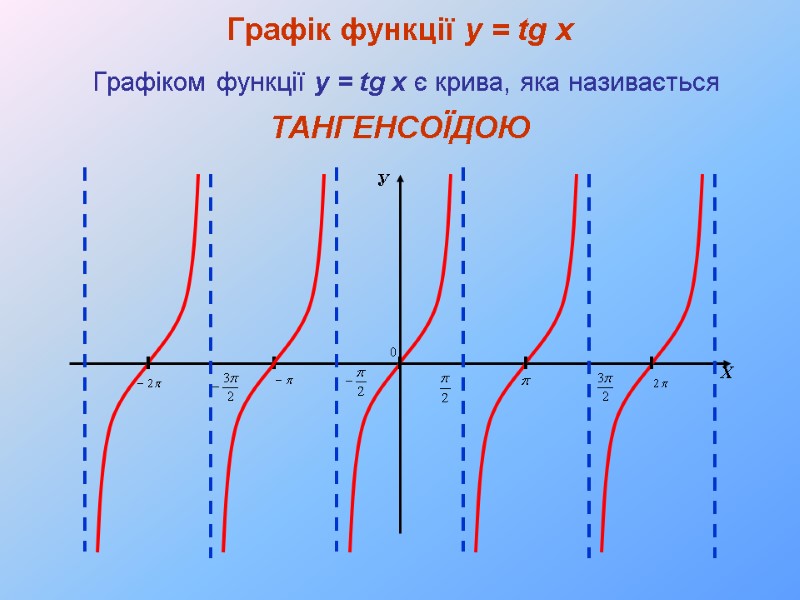
>Графік функції y = tg x Графіком функції y = tg x є Графік функції y = tg x Графіком функції y = tg x є крива, яка називається У Х ТАНГЕНСОЇДОЮ

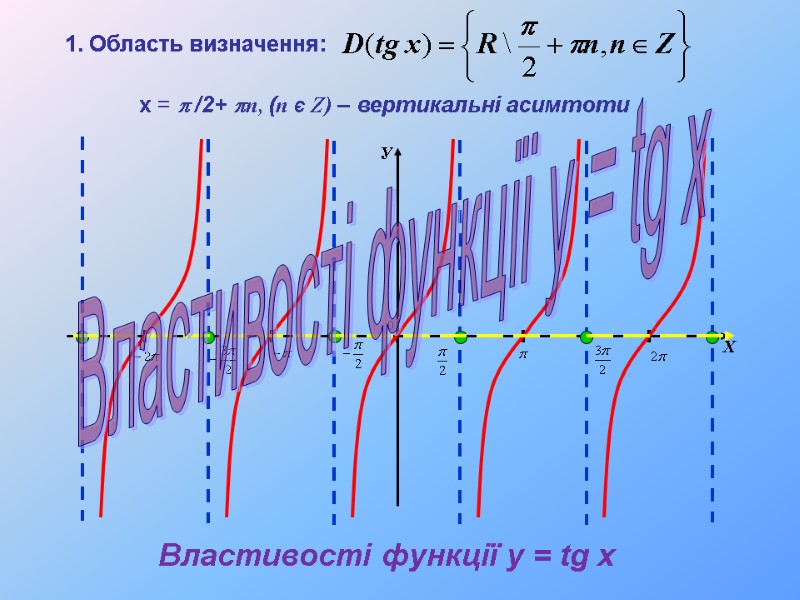
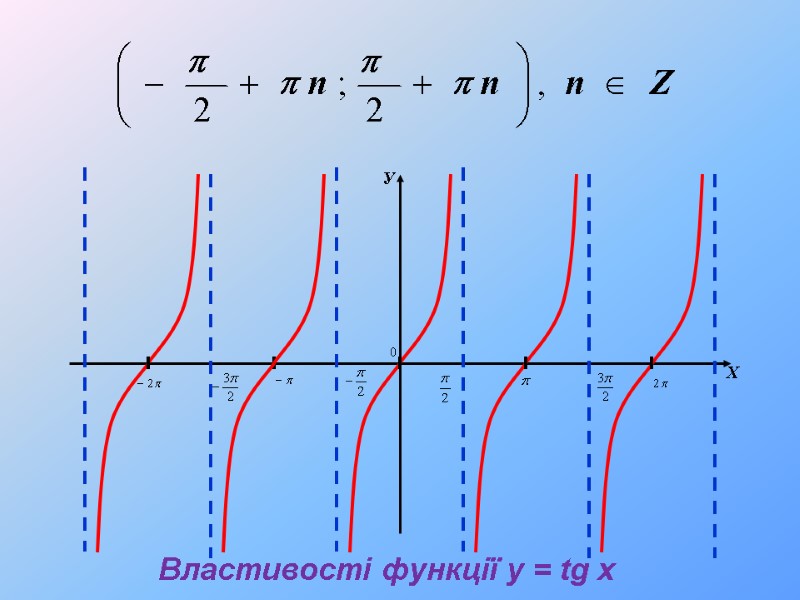
>Властивості функції y = tg x х = p /2+ pn, (n Є Z) Властивості функції y = tg x х = p /2+ pn, (n Є Z) – вертикальні асимтоти 1. Область визначення: Властивості функції y = tg x

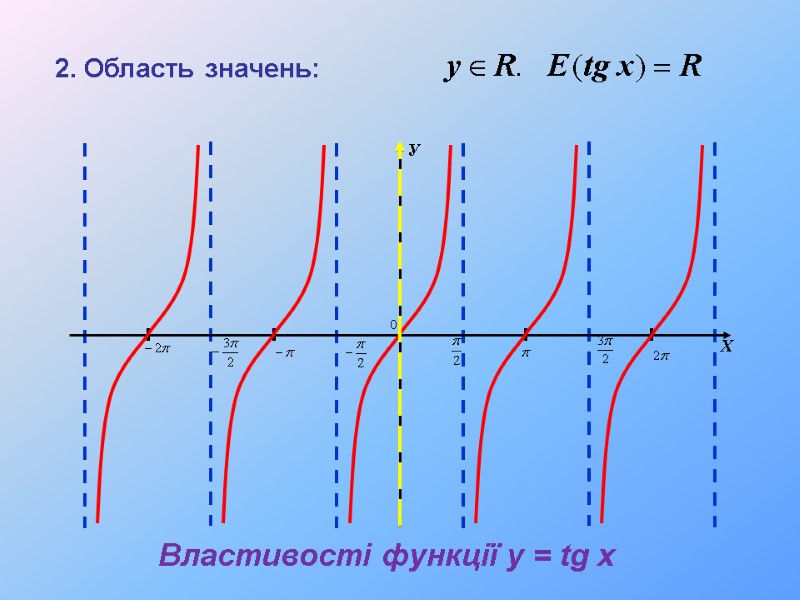
>2. Область значень: Властивості функції y = tg x 2. Область значень: Властивості функції y = tg x

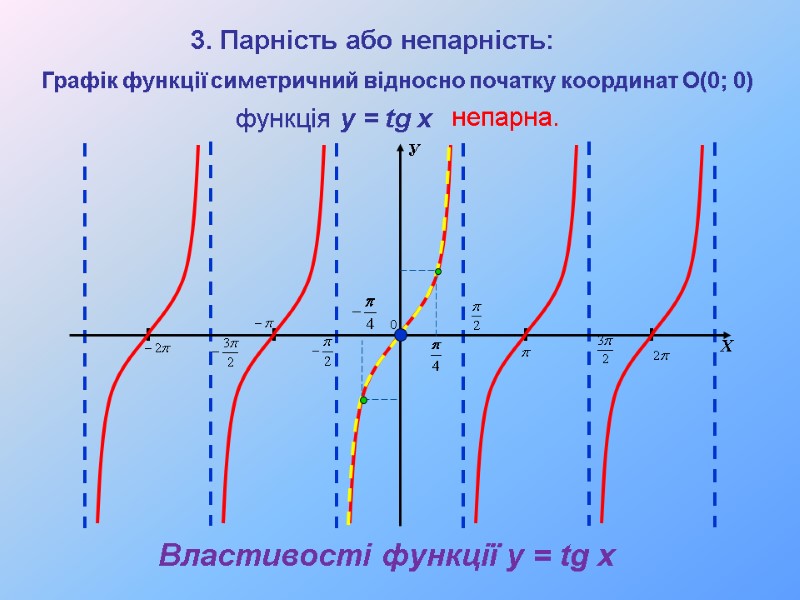
>Властивості функції y = tg x Графік функції симетричний відносно початку координат О(0; 0) Властивості функції y = tg x Графік функції симетричний відносно початку координат О(0; 0) 3. Парність або непарність: функція y = tg x непарна.

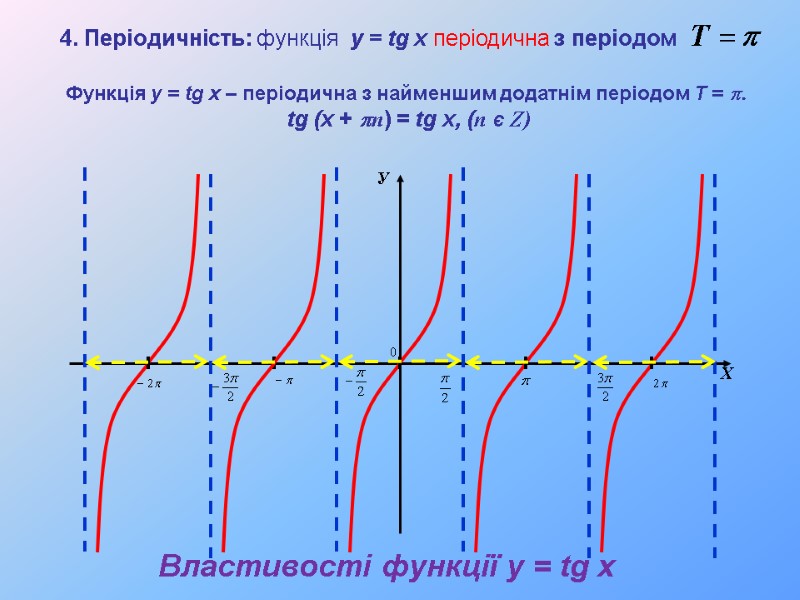
>У Х Функція y = tg x – періодична з найменшим додатнім періодом T У Х Функція y = tg x – періодична з найменшим додатнім періодом T = p. tg (x + pn) = tg x, (n Є Z) 4. Періодичність: функція y = tg x періодична з періодом Властивості функції y = tg x

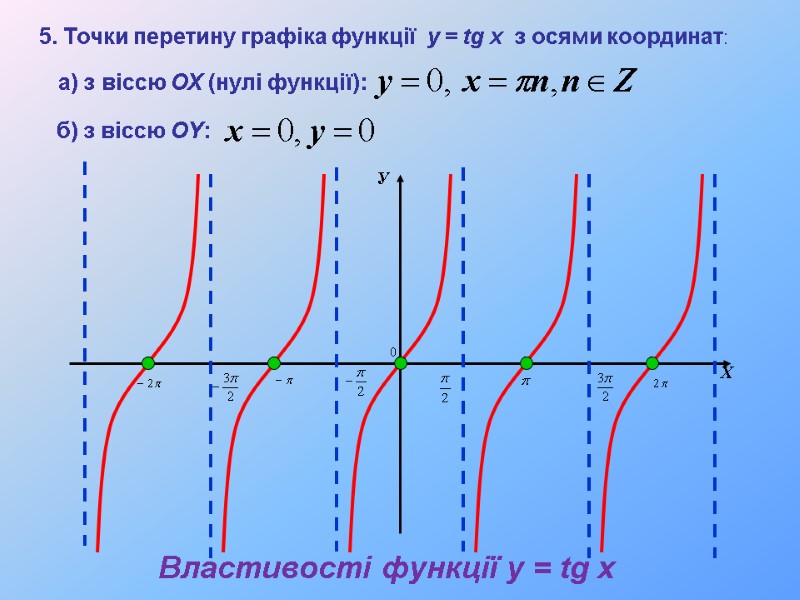
>У Х 5. Точки перетину графіка функції y = tg x з У Х 5. Точки перетину графіка функції y = tg x з осями координат: а) з віссю ОХ (нулі функції): б) з віссю ОY: Властивості функції y = tg x

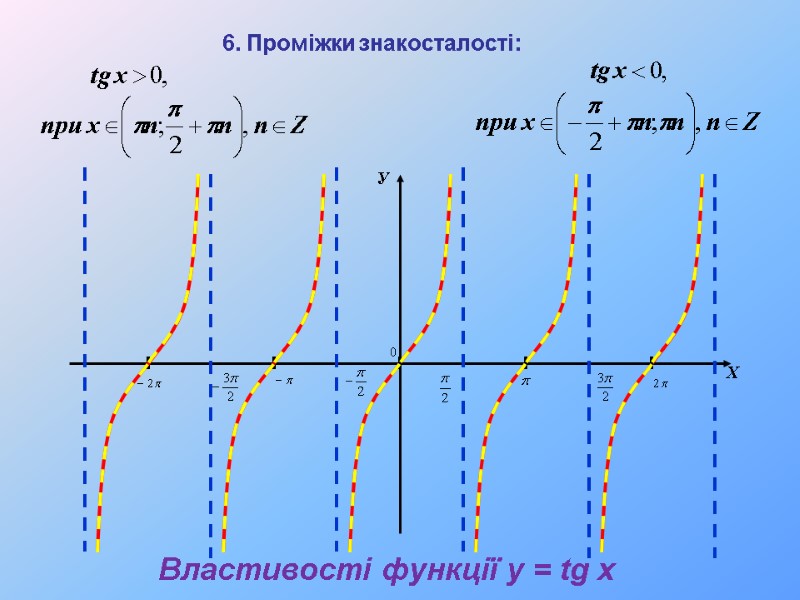
>У Х 6. Проміжки знакосталості: Властивості функції y = tg x У Х 6. Проміжки знакосталості: Властивості функції y = tg x

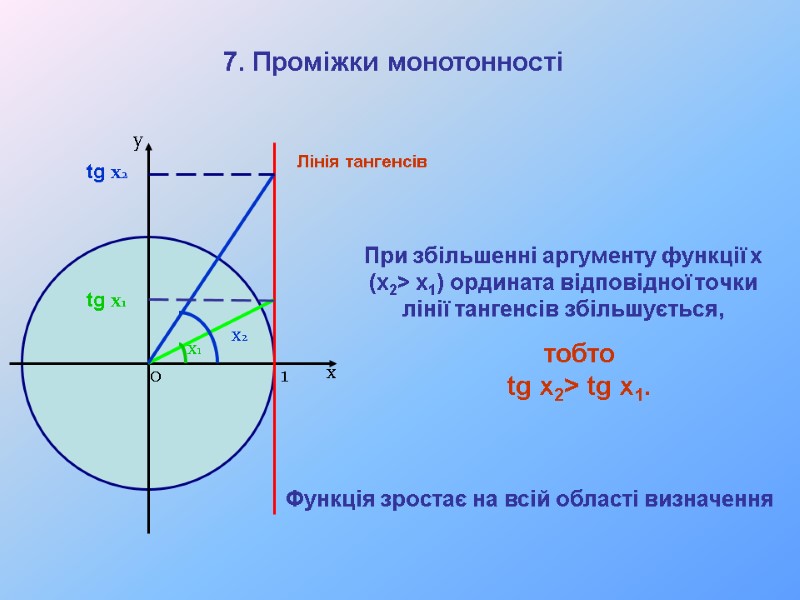
>При збільшенні аргументу функції х (x2> x1) ордината відповідної точки лінії тангенсів збільшується, При збільшенні аргументу функції х (x2> x1) ордината відповідної точки лінії тангенсів збільшується, х у x1 x2 tg x2 tg x1 7. Проміжки монотонності 1 0 Функція зростає на всій області визначення тобто tg x2> tg x1. Лінія тангенсів

>У Х Властивості функції y = tg x У Х Властивості функції y = tg x

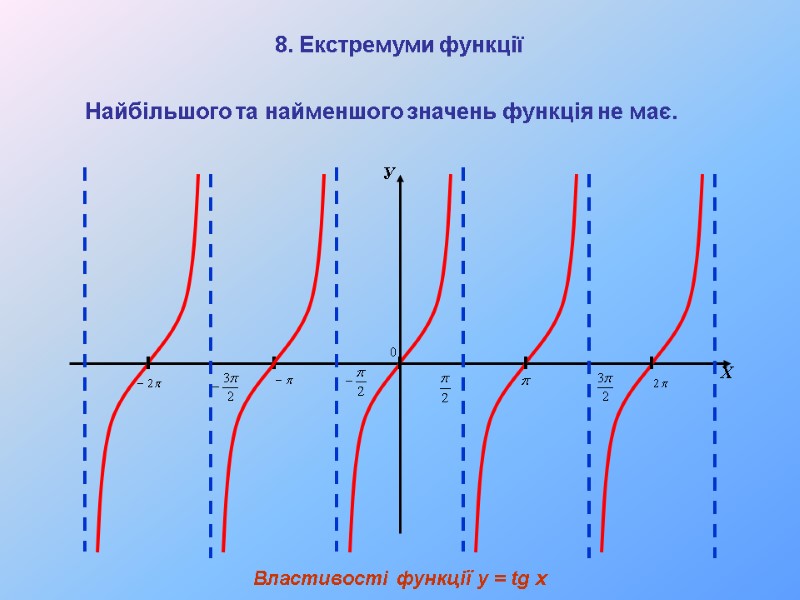
>У Х Властивості функції y = tg x Найбільшого та найменшого значень функція не У Х Властивості функції y = tg x Найбільшого та найменшого значень функція не має. 8. Екстремуми функції

>Виконання вправ на закріплення властивостей функції у= tg x Вправа 1. Користуючись властивостями функції Виконання вправ на закріплення властивостей функції у= tg x Вправа 1. Користуючись властивостями функції у= tg x, порівняйте числа: tg 150 і tg 1400 tg (-1,2 p) і tg (-0,1p) і Вправа 2. Розташуйте числа в порядку їх зростання: tg(-1,3); tg 0,7; tg 1,5. Властивості функції y = tg x

>Перевір правильність виконання та запис пояснень до вправ: Вправа 1 Розв’язання Оскільки tg 1400= Перевір правильність виконання та запис пояснень до вправ: Вправа 1 Розв’язання Оскільки tg 1400= tg (900+500)= tg 500 і функція у= tg x зростає на проміжку (-p/2; p /2) і 150 < 500, то tg 150 < tg 500. Отже, tg 150 < tg 1400. Оскільки tg (-1,2 p)=tg (-p - 0,2p) = tg (- 0,2 p) і функція у= tg x зростає на проміжку (-p /2; p /2) і - 0,2 p < - 0,1 p, то tg (- 0,2 p) < tg (- 0,1 p) . Отже, tg (- 1,2 p) < tg (- 0,1 p). Оскільки tg (10p/9)=tg (p + p/9) = tg (p/9) і функція у= tg x зростає на проміжку (-p /2; p /2) і 2p/9 > p/9 , то tg 2p/9 > tg p/9 . Отже, tg 2p/9 > tg 10p/9 . Вправа 2 Розв’язання Оскільки функція у= tg x зростає на проміжку (p/2; p /2) і -1,3<0,7<1,5 то tg (-1,3) < tg 0,7 < tg 1,5. Отже, tg (-1,3) < tg 0,7 < tg 1,5. Властивості функції y = tg x

>Виконай самостійно: Вправа 1. Користуючись властивостями функції у= tg x, порівняйте числа: Виконай самостійно: Вправа 1. Користуючись властивостями функції у= tg x, порівняйте числа: tg(-2, 6 p) і tg(-2, 6 1p) tg 2 і tg 3 tg 2, 7 і tg 2, 75 tg 1 і tg 1,5 Вправа 2. Розташуйте числа в порядку їх зростання: tg 250; tg 650; tg 150. tg(-1); tg (-3); tg (-2) . tg(-3); tg (-5); tg 3. Перевір Відповіді: Вправа 1. tg(-2, 6 p) > tg(-2, 6 1p) tg 2 < tg 3 tg 2, 7 < tg 2, 75 tg 1 < tg 1,5 Вправа 2. tg 150; tg 250; tg 650. tg(-3); tg (-2); tg (-1); . tg(-5); tg (-3); tg 3. Властивості функції y = tg x

>Перетворення графіків функції y = tg x Перетворення графіків функції y = tg x

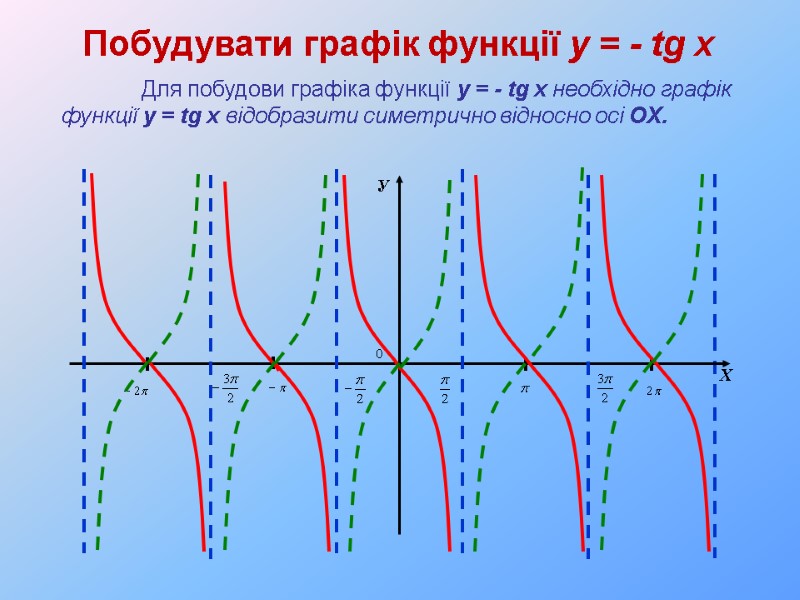
>Побудувати графік функції y = - tg x Для побудови графіка функції y Побудувати графік функції y = - tg x Для побудови графіка функції y = - tg x необхідно графік функції y = tg x відобразити симетрично відносно осі OX.

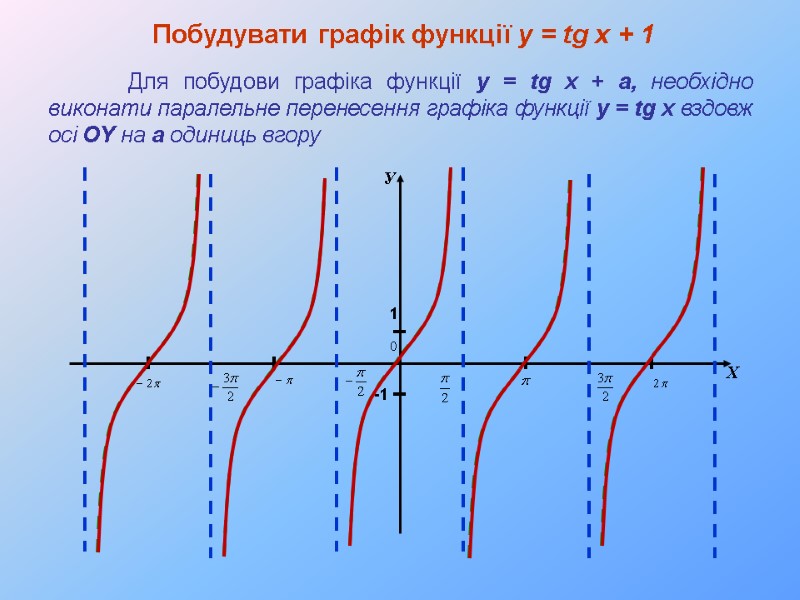
>Побудувати графік функції y = tg x + 1 Для побудови графіка функції Побудувати графік функції y = tg x + 1 Для побудови графіка функції y = tg x + а, необхідно виконати паралельне перенесення графіка функції y = tg x вздовж осі OY на а одиниць вгору

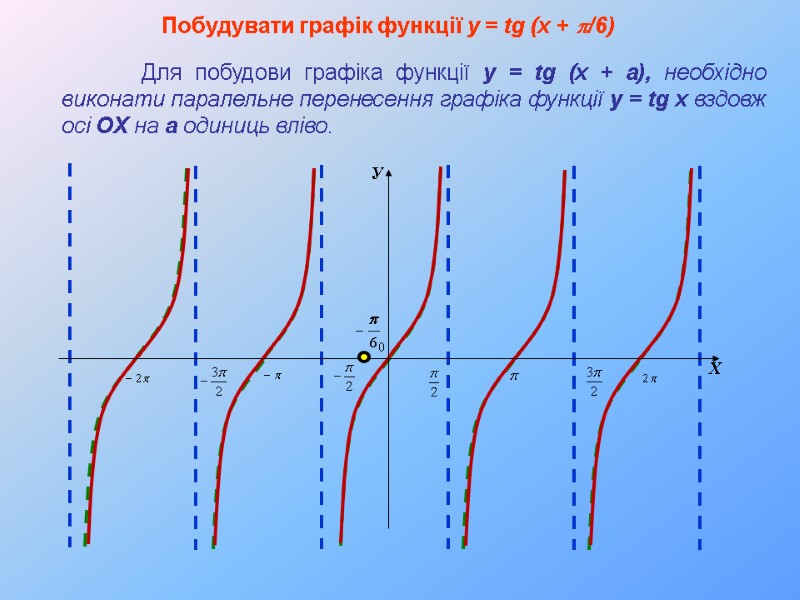
>Побудувати графік функції y = tg (x + p/6) Для побудови графіка функції Побудувати графік функції y = tg (x + p/6) Для побудови графіка функції y = tg (x + а), необхідно виконати паралельне перенесення графіка функції y = tg x вздовж осі OX на а одиниць вліво.

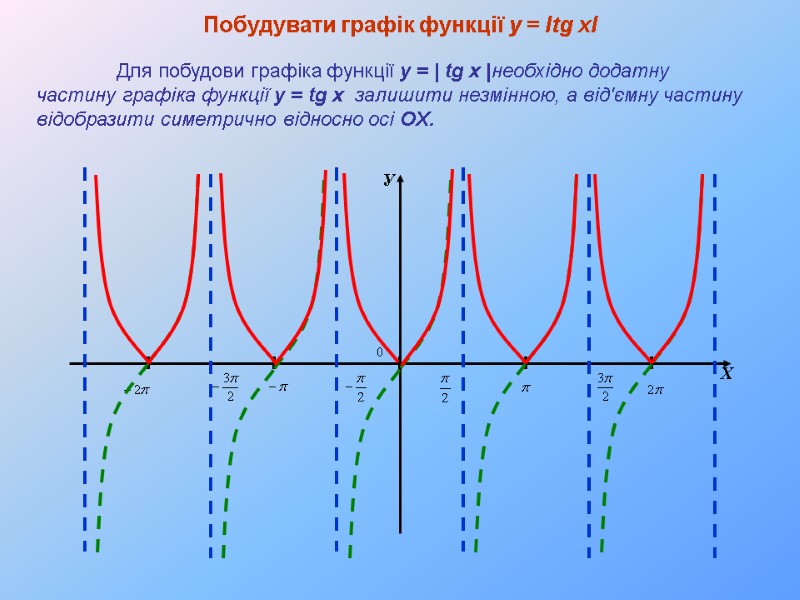
>У Х Побудувати графік функції y = Іtg xІ Для побудови графіка функції У Х Побудувати графік функції y = Іtg xІ Для побудови графіка функції y = | tg x |необхідно додатну частину графіка функції y = tg x залишити незмінною, а від'ємну частину відобразити симетрично відносно осі OX.

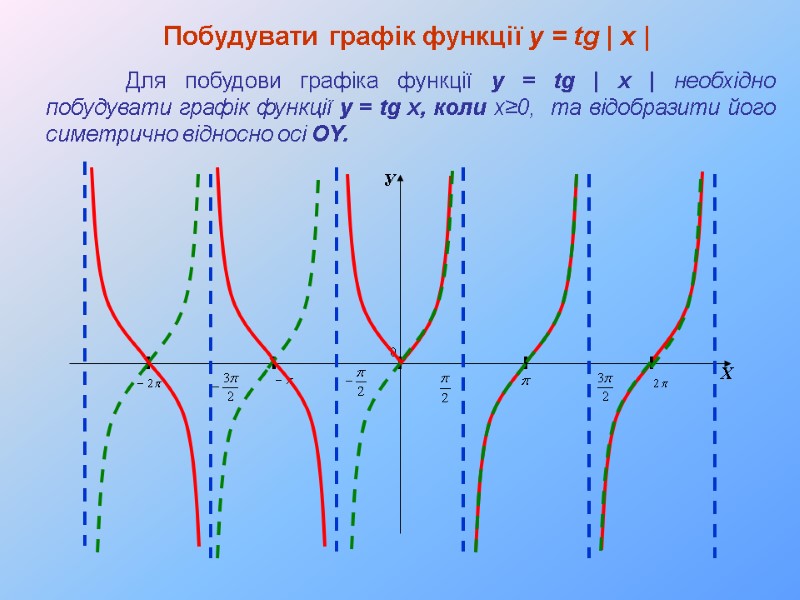
>У Х Побудувати графік функції y = tg | x | Для побудови У Х Побудувати графік функції y = tg | x | Для побудови графіка функції y = tg | x | необхідно побудувати графік функції y = tg x, коли x≥0, та відобразити його симетрично відносно осі OY.

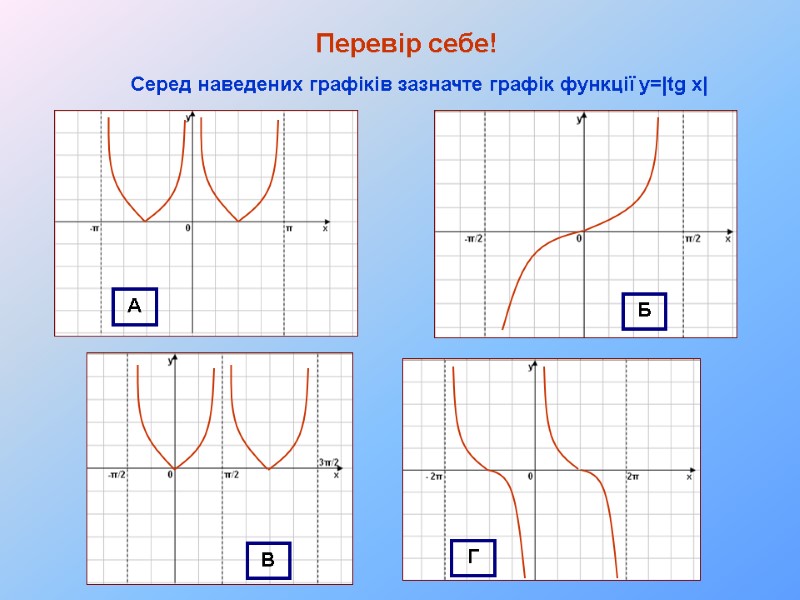
>Перевір себе! Серед наведених графіків зазначте графік функції y=|tg x| А Б В Г Перевір себе! Серед наведених графіків зазначте графік функції y=|tg x| А Б В Г

>Перевір себе! 1. Функція y=2tg x зростає на проміжку: 2. Графік функція y = Перевір себе! 1. Функція y=2tg x зростає на проміжку: 2. Графік функція y = tgx паралельно перенесли на 2 одиниці вниз вздовж осі Oy і на π/4 одиниці вліво вздовж осі Ox. Отримали наступний графік функції: