Функция y f x непрерывная на на промежутке Х называется

Функция y=f(x), непрерывная на на промежутке Х, называется выпуклой вниз (вогнутой) на промежутке Х, если для любых х1, х2 из этого промежутка выполняется неравенство:

Функция y=f(x) называется выпуклой вверх на промежутке Х, если для любых х1, х2 из этого промежутка выполняется неравенство:

Функция выпукла вверх (вниз) на промежутке Х тогда и только тогда, когда ее первая производная на этом промежутке монотонно возрастает (убывает).

Если вторая производная дифференцируемой функции положительна (отрицательна) на некотором промежутке Х, то функция выпукла вниз (вверх) на этом промежутке.

Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, на которых функция выпукла вверх и вниз. Точка перегиба – это точка экстремума первой производной.

Вторая производная дифференцируемой функции в точке перегиба х0 равна нулю:

Если вторая производная дифференцируемой функции в точке х0 меняет свой знак, то х0 - точка перегиба ее графика.

1 Найти вторую производную функции. 2 Найти точки, в которых вторая производная функции равна нулю или не существует.

3 Исследовать знак второй производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и точках перегиба. 4 Найти значения функции в точках перегиба.

Найти интервалы выпуклости и точки перегиба функции

1 2 Находим вторую производную: Находим точки, в которых вторая производная обращается в нуль:

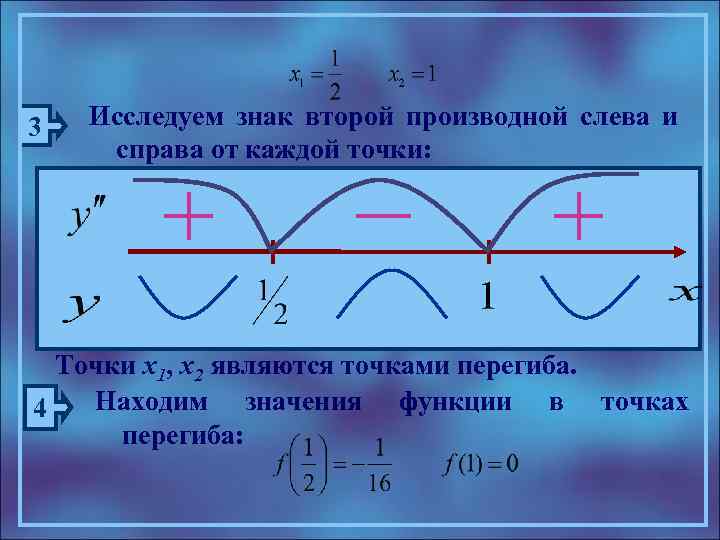3 Исследуем знак второй производной слева и справа от каждой точки: Точки х1, х2 являются точками перегиба. Находим значения функции в точках 4 перегиба:

Свойства выпуклых Функций 1) Если функция f(x) выпуклая вверх(вниз), то функция –f(x) является выпуклой вниз(вверх). 2) Произведение выпуклой вверх(вниз) функции на положительную постоянную также является выпуклой вверх(вниз) функцией.

3) Сумма двух выпуклых вверх(вниз) функций также является выпуклой вверх(вниз) функцией. 4) Пусть функция y=g(u) выпуклая вниз(вверх) и возрастающая, а функция u=f(x) также выпуклая вниз(вверх). Тогда сложная функция y=g(f(x)) будет выпуклой вниз (вверх).

5) Пусть функции f(x) и g(x) являются в соответствующих промежутках взаимно обратными функциями. Тогда: а) Если f(x) выпуклая вверх и возрастает, то функция g(x) выпуклая вниз и возрастает. б) Если f(x) выпуклая вверх и убывает, то функция g(x) выпуклая вверх и убывает. в) Если f(x) выпуклая вниз и убывает, то g(x) выпуклая вниз и убывает. г) Если f(x) выпуклая вниз и возрастает, то g(x) выпуклая вверх и возрастает.

6) Выпуклая вверх(вниз) на отрезке [a; b] функция f(x), отличная от постоянной, не может достигать наименьшего(наибольшего) значения во внутренней точке отрезка [a; b]. 7) Если каждая из функций F 1(x), . . . Fn(x), выпуклая вверх на некотором промежутке и принимает только неотрицательные значения, то функция, равная корню n-ной степени из произведения всех этих функций, также является выпуклой вверх на этом промежутке.

Применение в. ф. при решении уравнений Для строго выпуклой вверх или вниз f(x) уравнение p*f(u) + q*f(v) = p*f(u 1) + q*f(v 1) равносильно совокупности уравнений u(x)=u 1(x), u(x)=v 1(x), если p*u + q*v = p*u 1 + q*v 1