Функция, позволяющая по величине одного признака (x) находить

Функция, позволяющая по величине одного признака (x) находить средние (ожидаемые) значения другого признака (y), связанного с x корреляционно, называется регрессией. Статистический анализ регрессии получил название регрессионного анализа.

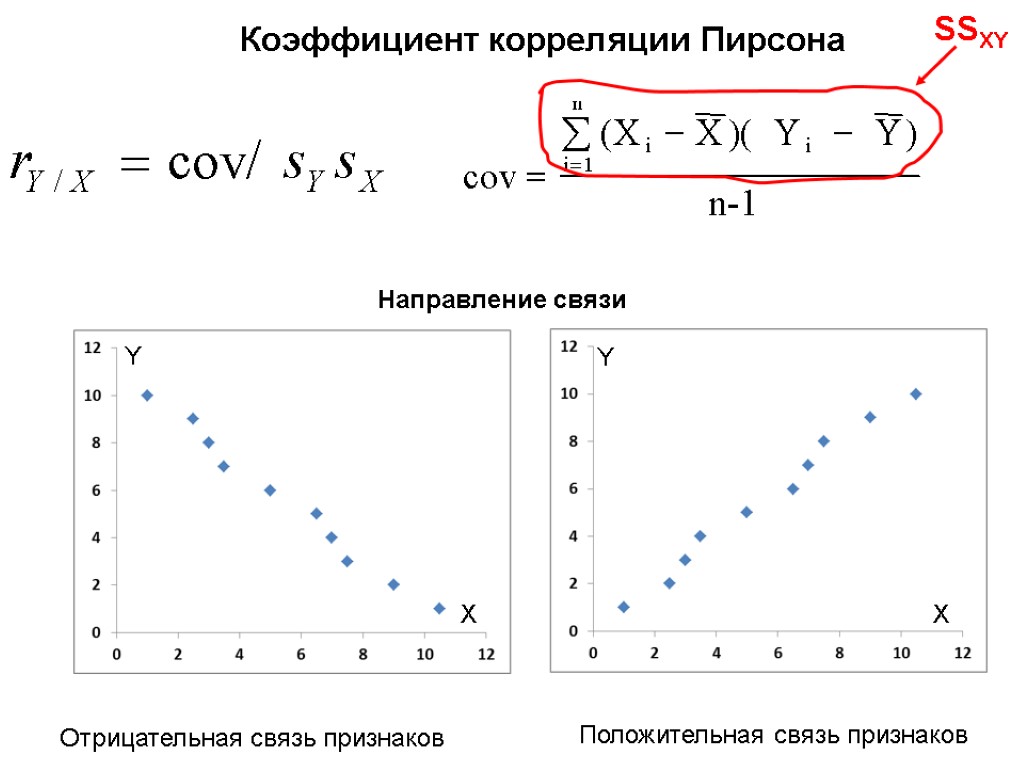
Коэффициент корреляции Пирсона Направление связи Положительная связь признаков Отрицательная связь признаков X Y X Y SSXY

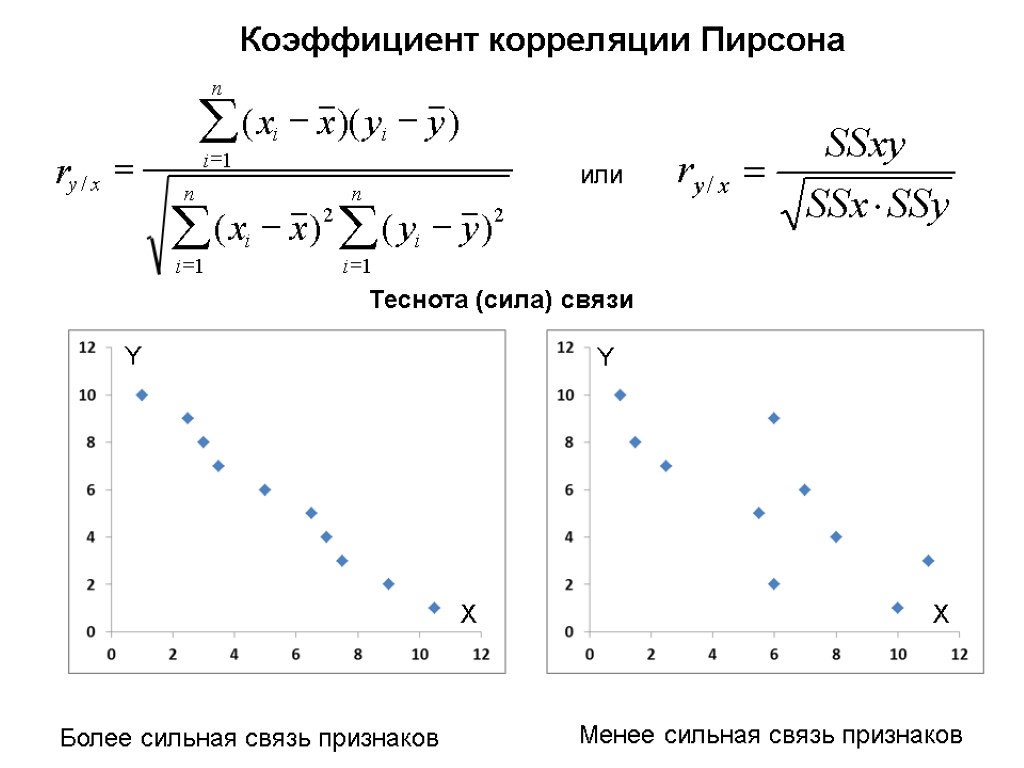
Коэффициент корреляции Пирсона или Теснота (сила) связи Менее сильная связь признаков Более сильная связь признаков X Y X Y

Регрессионные модели: Линейная регрессия Уравнение прямой линии Y = a + b*X, где Y – «Y с крышечкой» - оценка среднего значения признака Y, соответствующего определенному значению признака X; a и b – коэффициенты уравнения. Нелинейная регрессия Все другие уравнения, например: Y = a*Xb – степенное уравнение Y = a*eX – экспоненциальное уравнение Y = a + b*Ln(X) – логарифмическое уравнение Y = a*x2 + b*x + c – полином второго порядка и т.д. … тогда можно предсказать любое Y = a + b*X, Функция, позволяющая по величине одного признака (x) находить средние (ожидаемые) значения другого признака (y), связанного с x корреляционно, называется регрессией…

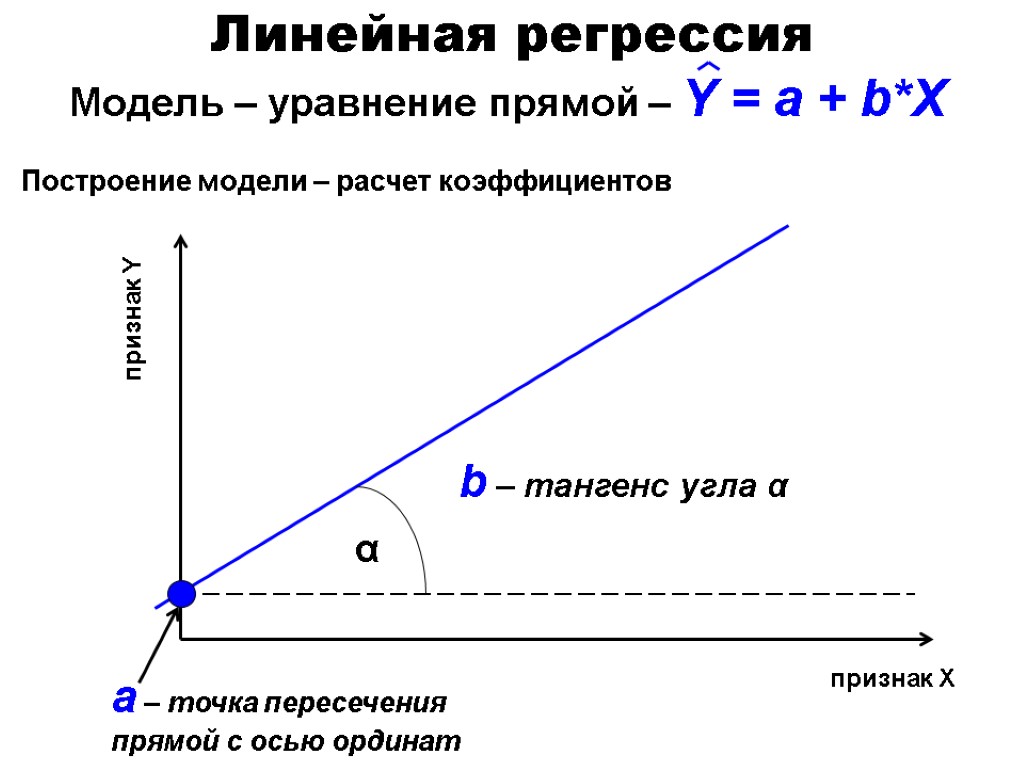
признак X признак Y α b – тангенс угла α a – точка пересечения прямой с осью ординат Линейная регрессия Модель – уравнение прямой – Y = a + b*X Построение модели – расчет коэффициентов

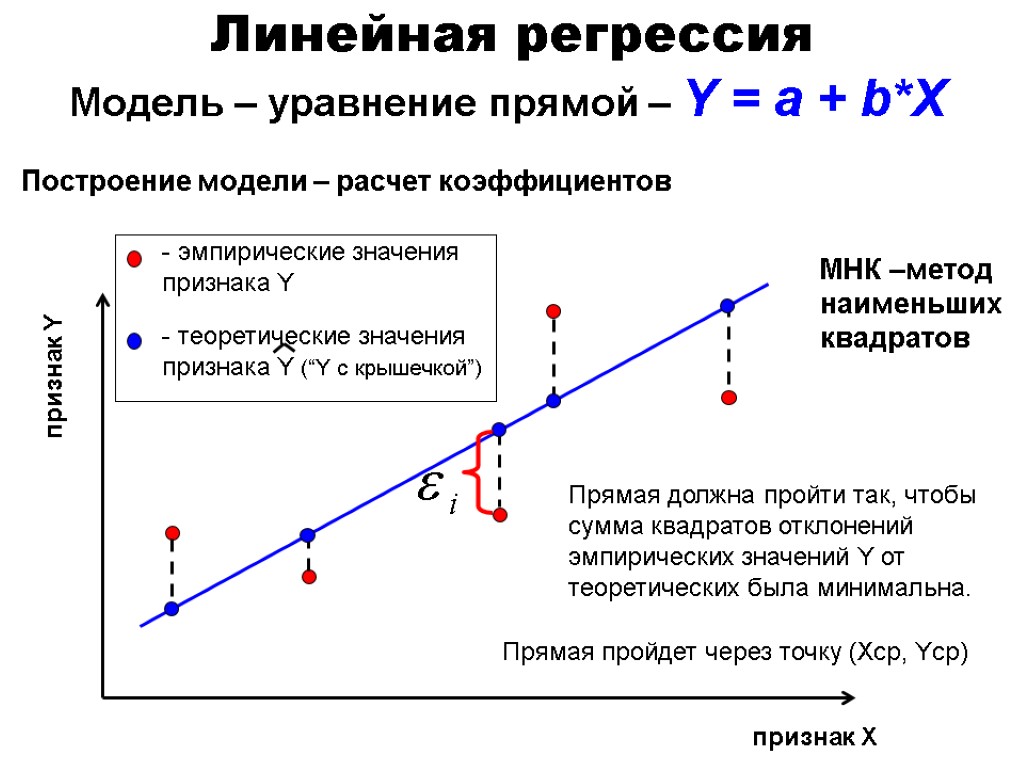
Линейная регрессия Модель – уравнение прямой – Y = a + b*X Построение модели – расчет коэффициентов признак X признак Y Прямая должна пройти так, чтобы сумма квадратов отклонений эмпирических значений Y от теоретических была минимальна. Прямая пройдет через точку (Xср, Yср) МНК –метод наименьших квадратов

Линейная регрессия Модель – уравнение прямой – Y = a + b*X МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК)

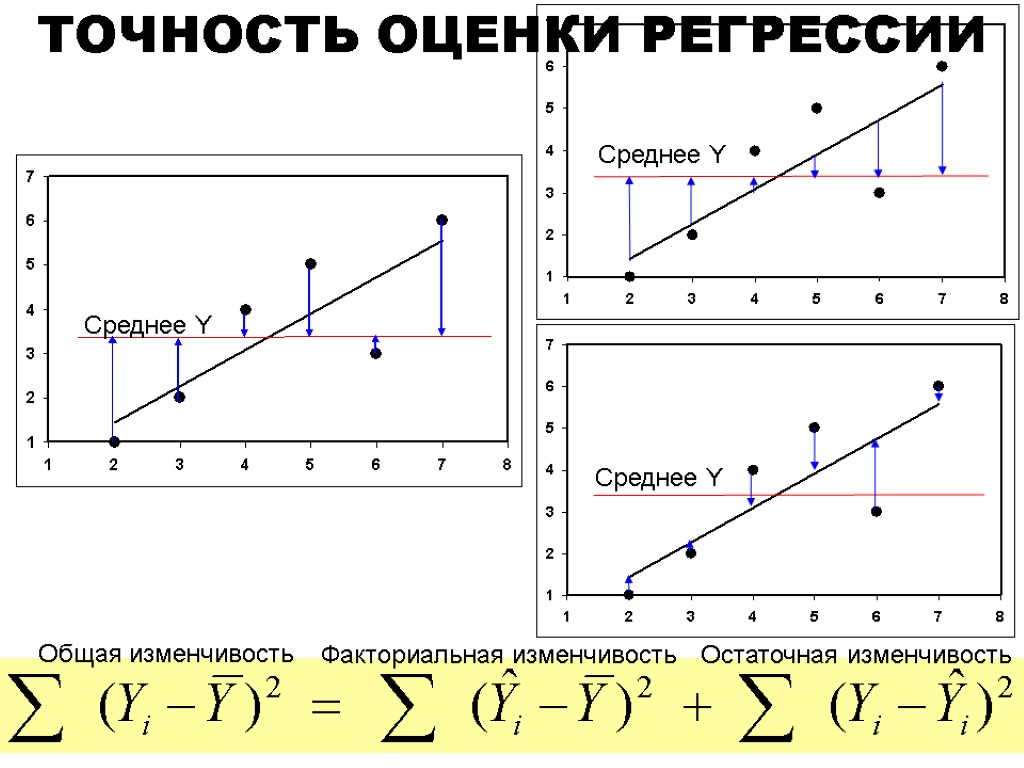
Среднее Y Среднее Y Среднее Y ТОЧНОСТЬ ОЦЕНКИ РЕГРЕССИИ Общая изменчивость Остаточная изменчивость Факториальная изменчивость

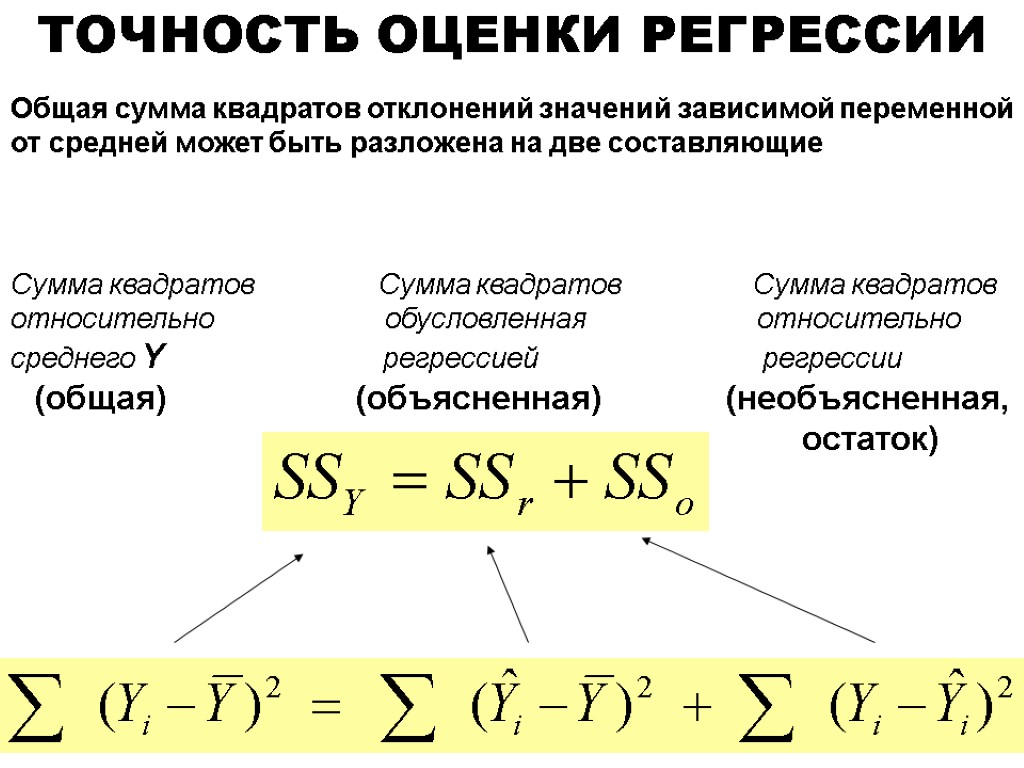
ТОЧНОСТЬ ОЦЕНКИ РЕГРЕССИИ Общая сумма квадратов отклонений значений зависимой переменной от средней может быть разложена на две составляющие Сумма квадратов Сумма квадратов Сумма квадратов относительно обусловленная относительно среднего Y регрессией регрессии (общая) (объясненная) (необъясненная, остаток)

КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ ТОЧНОСТЬ ОЦЕНКИ РЕГРЕССИИ Общая сумма квадратов отклонений значений зависимой переменной от средней может быть разложена на две составляющие: Сумма квадратов Сумма квадратов Сумма квадратов относительно обусловленная относительно среднего Y регрессией регрессии (общая) (объясненная) (необъясненная, остаток)

Коэффициент корреляции Пирсона в квадрате (для случая линейной связи только) КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ Сумма квадратов Сумма квадратов Сумма квадратов относительно обусловленная относительно среднего Y регрессией регрессии (общая) (объясненная) (необъясненная, остаток)

ОШИБКА УРАВНЕНИЯ РЕГРЕССИИ А. Стандартная ошибка углового коэффициента Б. Стандартная ошибка свободного члена уравнения

ОЦЕНКА ДОСТОВЕРНОСТИ УРАВНЕНИЯ РЕГРЕССИИ Нулевая гипотеза сохраняется, если соблюдается равенство: Достоверность наклона линии регрессии НО: В генеральной совокупности нет изменений значений функции по оси аргумента. Следовательно, наблюдаемое отличие углового коэффициента (b) от нуля случайно. H1: угловой коэффициент по модулю больше 0.

НО: В генеральной совокупности регрессионной связи нет и наблюдаемое отличие коэффициента детерминации от нуля случайно. Н1: коэффициент детерминации больше нуля. Нулевая гипотеза отвергается, если: При соблюдении этого условия коэффициент детерминации с вероятностью отличается от нуля на выбранном уровне значимости Достоверность коэффициента детерминации ОЦЕНКА ДОСТОВЕРНОСТИ УРАВНЕНИЯ РЕГРЕССИИ