Функция нескольких переменных Лекция

Функция нескольких переменных Лекция 1/21/2018 1

Функция нескольких переменных Пусть X = {(x 1, x 2 , …, xn) | xi Xi ℝ } , U ℝ. ОПРЕДЕЛЕНИЕ Функция f : X U называется функцией n переменных u = f (x 1, x 2 , …, xn) , где f – закон, задающий соответствие между x 1, x 2 , …, xn и u. Значение u = f(x 1, x 2 , …, xn) при x 1 = x 01, x 2 = x 02, …, xn = x 0 n записывают в виде u = f(x 01, x 02 , …, x 0 n) или 1/21/2018 2

Геометрическое изображение функции двух переменных • Пусть функция • z = f (х, у) (1) • определена в некоторой области D на плоскости хоу. • Множество точек P (х, у, f (х, у)), определяемое уравнением (1), - геометрический образ функции двух переменных – это поверхность, которая проектируется в область D. • Точка М является проекцией точки Р. 1/21/2018 3

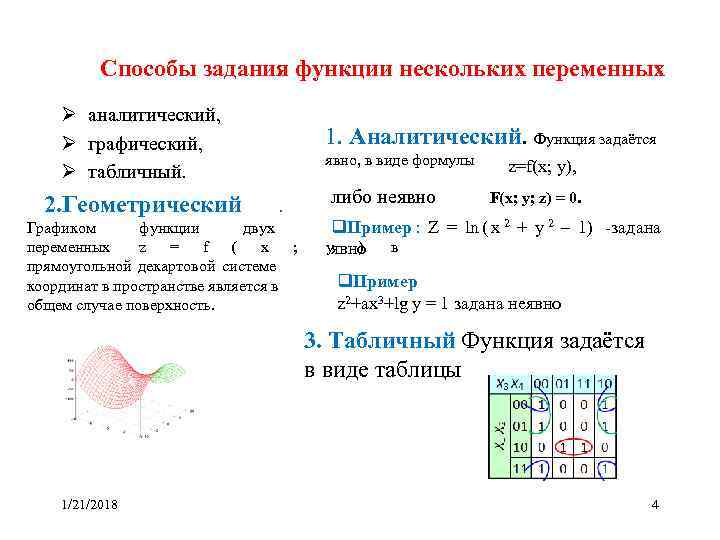
Способы задания функции нескольких переменных Ø аналитический, Ø графический, 1. Аналитический. Функция задаётся явно, в виде формулы z=f(x; y), Ø табличный. 2. Геометрический . либо неявно F(x; y; z) = 0. Графиком функции двух q. Пример : Z = ln ( x 2 + y 2 – 1) -задана переменных z = f ( x ; yявно ) в прямоугольной декартовой системе координат в пространстве является в q. Пример общем случае поверхность. z 2+ax 3+lg y = 1 задана неявно 3. Табличный Функция задаётся в виде таблицы 1/21/2018 4

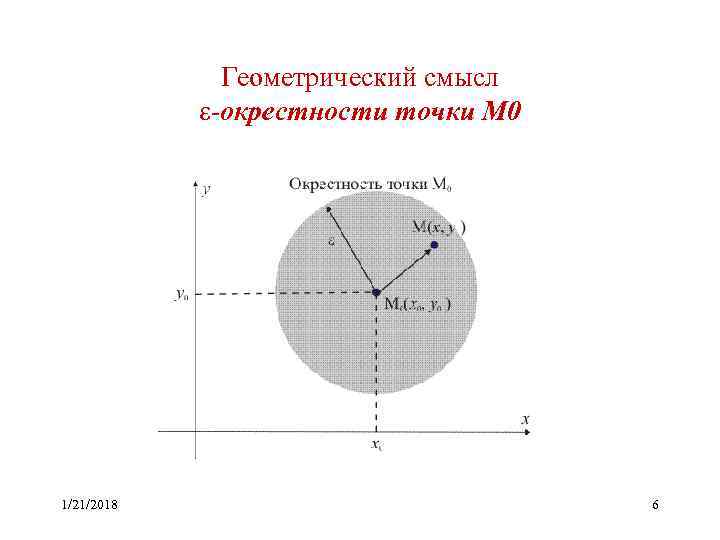
-окрестность точки • Определение Множество точек ℝ n , находящихся от M 0 на расстоянии меньшем , называется -окрестностью точки M 0. Обозначим U(M 0, ). При n = 1 -окрестность точки M 0 U(M 0, ) = {M Ox | |M 0 M| = |x – x 0| < } = (x 0 – , x 0 + ). -окрестность точки M 0 ℝn без точки M 0 будем называть проколотой -окрестностью и обозначать U*(M 0, ) 1/21/2018 5

Геометрический смысл -окрестности точки М 0 1/21/2018 6

• Определение Точка A(х, у) называется граничной для некоторой области G , если в её окрестности есть как точки, принадлежащие области G , так и точки, не содержащиеся в области G. • Определение Множество граничных точек образует границу области G Определение Если граница принадлежит области D , то область называется замкнутой (границу будем обозначать сплошной линией). В противном случае область D – открытая (не замкнутая). В этом случае границу будем обозначать 1/21/2018 пунктирной линией. 7

q Пример Пусть дана функция z = ln(x-y). Логарифмическая функция определена только при положительном значении аргумента. Значит, – это часть плоскости хоу справа от линии (границы области) у = х, сама граница не принадлежит области D • Определение. Точка А называется внутренней точкой множества G , если существует - окрестность точки , целиком принадлежащая множеству (т. е. ) 1/21/2018 8

Предел функции нескольких переменных Ø Определение Число A ℝ называется пределом . функции f(x) при x стремящемся к x 0, если >0 такое, что если x U*(x 0, ) , то f(x) U(A, ). Ø Определение d - окрестностью т. М 0 называется круг с центром в т. М 0 и радиусом : Определение Число А ℝ называется пределом функции z = f(x; y) = f(M), если для любого числа >0 1/21/2018 9

ü Замечания 1) Условие M U*(M 0, ) означает, что выполняется : 2) Условие f(M) U(A, ) означает, что для f(M) выполняется неравенство | f(M) – A | < 3) Определение предела функции n переменных не отличается от определения предела функции одной переменной, 4) Утверждения, которые были получены о пределах функции одной переменной, остаются верными и для предела функции n переменных. 1/21/2018 10

1/21/2018 11

1/21/2018 12

Пример Вычислить пределы функций • получим очень полезные неравенства : 1/21/2018 13

ü Замечание При кажущейся полной аналогии понятий предела функций одной и двух переменных существует глубокое различие между ними. ü В случае функции одной переменной для существования предела в точке необходимо и достаточно равенство лишь двух чисел – пределов по двум направлениям: справа и слева от предельной точки. ü Для функции двух переменных стремление к предельной точке на плоскости может происходить по бесконечному числу направлений (и необязательно по прямой. 1/21/2018 14

Теоремы о пределах • Определение. Число А называют пределом функции при и , • если • такое, что из неравенств и следует неравенство . • Этот факт коротко записывают так: Теорема Если существуют , то: где предельная точка может быть конечной или бесконечной. 1/21/2018 15

Непрерывность функции нескольких переменных Пусть u = f(M) определена в некоторой окрестности M 0 ℝn. ОПРЕДЕЛЕНИЕ Функция f ( M ) называется непрерывной в точке M 0 если справедливо равенство 1) арифметические операции над непрерывными в точке M 0 функциями приводят к непрерывным в этой точке функциям 2) сложная функция, составленная из нескольких непрерывных функций, тоже будет непрерывной. Если функция u = f(M) определена в некоторой окрестности точки M 0 (за исключением, может быть, самой M 0 ), но не является в этой точке непрерывной, то ее называют разрывной в точке M 0, а саму точку M 0 – точкой разрыва. 1/21/2018 16

Теорема Если функция определена в некоторой окрестности точки и непрерывна в этой точке, то она непрерывна в этой точке по каждой из . переменных. • Обратное утверждение неверно. • Пример. Докажем, что функция непрерывна в точке по каждой переменной и , но не является непрерывной в этой точке по совокупности переменных. это означает, что непрерывна в точке 0(0, 0) по переменной Покажем, что предел не существует приближаясь к точке 0(0, 0) по различным прямым, соответствующим разным значениям k получаем разные предельные значения Отсюда следует, что предел данной функции не существует, функция не непрерывна 1/21/2018 17

q Определение Область состоящая только из внутренних точек, называется открытой областью. q Определение Область состоящая из внутренних точек и всех граничных точек, называется замкнутой областью. q Определение Функция называется непрерывной в области D, если она непрерывна в каждой внутренней точке этой области. q Определение Функция называется непрерывной в замкнутой области , если она непрерывна в каждой внутренней точке этой области и на её границе. 1/21/2018 18

Частные производные Пусть z = f(x, y) , D(z) = D x. Oy , D – открытая область. Пусть M 0(x 0, y 0) D. Придадим x 0 приращение x, оставляя значение y 0 неизмененным (так, чтобы точка M(x 0 + x, y 0) D). При этом z = f(x, y) получит приращение x z(M 0) = f(M) – f(M 0) = f(x 0 + x, y 0) – f(x 0, y 0). x z ( M 0 ) называется частное приращение функции z = f ( x , y ) по x в точке M 0(x 0, y 0). 1/21/2018 19

ОПРЕДЕЛЕНИЕ Предел (если он существует и конечен) называется частной производной функции z = f ( x , y ) по переменной x в точк M 0(x 0, y 0). Обозначают: или Операция нахождения для функции z = f(x, y) ее частных производных называется дифференцированием функции z = f(x, y) по переменной x и y соответственно 1/21/2018 20

ü Замечания 1) Обозначения и целые символы. Отдельно взятые выражения z(x 0, y 0) и x смысла не имеют. 2) характеризует скорость изменения функции z = f(x, y) по x в точке M 0(x 0, y 0) (физический смысл частной производной по x). Аналогично определяется частная производная функции z = f(x, y) по переменной y в точке M 0(x 0, y 0): Обозначают: 1/21/2018 21

• Найти частные производные функции • Замечание Таким образом, частная производная функции по какой-либо переменной является производной функции этой одной переменной при фиксированных значениях других переменных. 1/21/2018 22

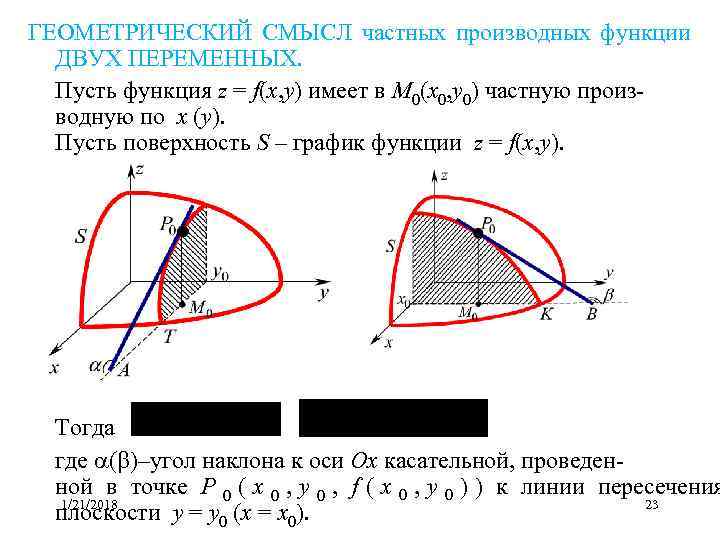
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ частных производных функции ДВУХ ПЕРЕМЕННЫХ. Пусть функция z = f(x, y) имеет в M 0(x 0, y 0) частную произ- водную по x (y). Пусть поверхность S – график функции z = f(x, y). Тогда где ( )–угол наклона к оси Ox касательной, проведен- ной в точке P 0 ( x 0 , y 0 , f ( x 0 , y 0 ) ) к линии пересечения 1/21/2018 23 плоскости y = y 0 (x = x 0).

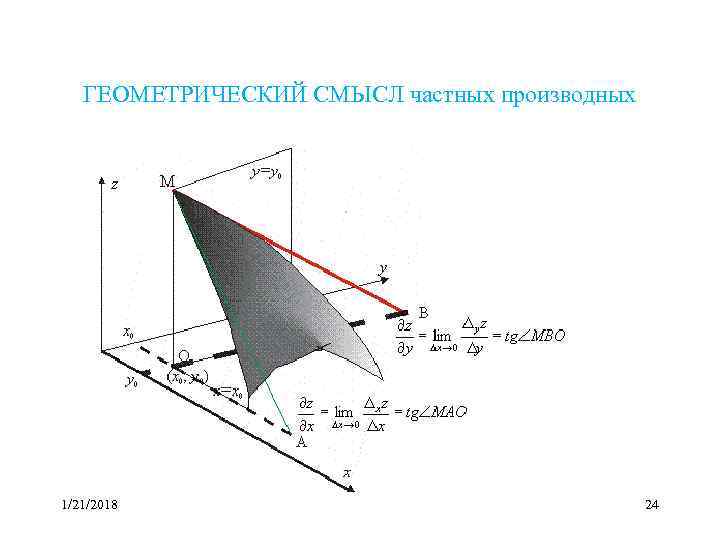
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ частных производных 1/21/2018 24

Частные производные высших порядков Пусть z = f ( x , y ) имеет и , определенные на D x. Oy. Функции и называют также частными производными первого порядка функции f(x, y) (или первыми частными производными функции f(x, y)). и в общем случае функции переменных x и y. Частные производные по x и по y от и , если они существуют, называются частными производ- ными второго порядка (или вторыми частными производ- ными) функции f(x, y). 1/21/2018 25

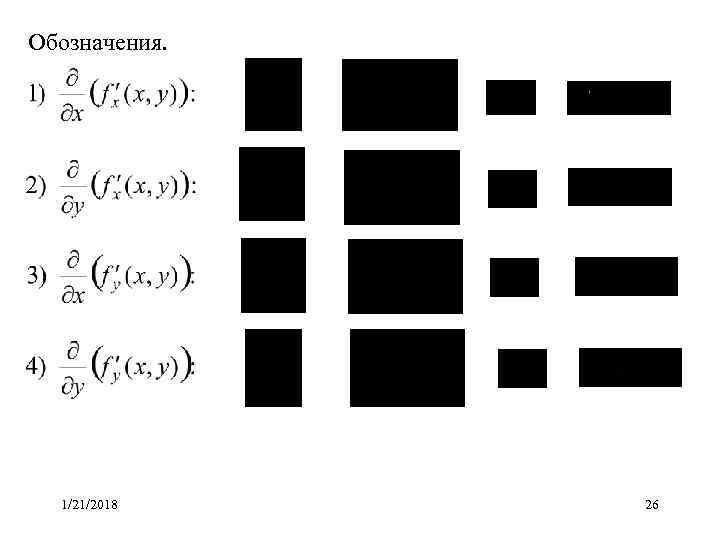
Обозначения. 1/21/2018 26

Частные производные второго порядка в общем случае являют- ся функциями двух переменных. Продолжая этот процесс, назовем частными производными порядка n функции z = f ( x , y ) частные производные от е частных производных (n – 1)-го порядка. Обозначения аналогичны обозначениям для частных производ - ных 2 -го порядка. Например: Частные производные порядка n > 1 называют частными производными высших порядков. Частные производные высших порядков, взятые по разным аргументам, называются смешанными. 1/21/2018 27

ТЕОРЕМА 1 ( условие независимости смешанной производной от последовательности дифференцирований). Пусть z = f(x, y) в некоторой области D x O y имеет все частные производные до n -го порядка включительно и эти производные непрерывны. Тогда смешанные производные порядка m (m n), отличающиеся лишь последовательностью дифференцирований, совпадают между собой. • Замечание Необходимым условием для существования частных производных является непрерывность функции по соответствующим аргументам. 1/21/2018 28

Дифференцируемость функций нескольких переменных Пусть z = f(x, y) , D(z) = D x. Oy , D – область (т. е. открытое связное множество). Пусть M 0(x 0, y 0) D. Придадим x 0 и y 0 приращение x и y соответственно (так, чтобы точка M(x 0 + x, y 0 + y) D). При этом z = f(x, y) получит приращение z(M 0) = f(M) – f(M 0) = f(x 0 + x, y 0 + y) – f(x 0, y 0). z(M 0) называется полным приращением функции z = f(x, y) в точке M 0(x 0, y 0), соответствующим x и y. 1/21/2018 29

ОПРЕДЕЛЕНИЕ. Функция z = f(x, y) называется дифференцируемой в точке M 0 ( x 0 , y 0 ) если ее полное приращение в этой точке может быть записано в виде z(M 0) = A x + B y + 1 x + 2 y , (1) где A, B – некоторые числа, 1, 2 – бесконечно малые при x 0, y 0 ü Замечание. Функции 1 и 2 зависят от x 0, y 0, x, y. Равенство (1) можно записать и в более сжатой форме: z(M 0) = A x + B y + , (2) где – бесконечно малая при 0. Функция z = f ( x , y ), дифференцируемая в каж некоторой области D, называется дифференцируемой в D. 1/21/2018 30

Напомним: для дифференцируемой функции y = f ( x ) справ ливы утверждения: 1) y = f(x) дифференцируема в x 0 f (x 0); 2) y = f(x) дифференцируема в x 0 y = f(x) непрерывна в x 0. ТЕОРЕМА (необходимые условия дифференцируемости ФНП) Пусть функция z = f(x, y) дифференцируема в точке M 0(x 0, y 0). Тогда она непрерывна в этой точке и имеет в ней частные производные по обеим независимым переменным. 1/21/2018 31

ü Замечания 1) С учетом теоремы равенства (1) и (2) можно записать соответственно в виде: (3) (4) где 1, 2 – бесконечно малые при x 0, y 0, – бесконечно малая при 0. 2) Утверждение обратное теореме неверно. Из непрерывности функции двух переменных в точке и существования в этой точке ее частных производных еще не следует дифференцируемость функции. 1/21/2018 32

ПРИМЕР Функция непрерывна в точке (0; 0) и имеет в этой точке частные производные, но не является в этой точке дифференцируемой. ТЕОРЕМА (достаточные условия дифференцируемости ФНП) Пусть функция z = f(x, y) имеет в некоторой окрестности точки M 0(x 0, y 0) частные производные и , причем в самой точке M 0 эти производные непрерывны. Тогда функция z = f(x, y) дифференцируема в этой точке. 1/21/2018 33

Дифференциал ФНП Пусть функция z = f(x, y) дифференцируема в точке M 0(x 0, y 0). Тогда где 1, 2 – бесконечно малые при x 0, y 0. ОПРЕДЕЛЕНИЕ Если z = f ( x , y ) дифференцируема в то M 0 ( x 0 , y 0 ) , то линейная относительно x и y часть ее пол ного приращения в этой точке, т. е. называется полным дифференциалом функции z = f(x, y) в точке M 0(x 0, y 0) и обозначается dz(M 0) или df(x 0, y 0). 1/21/2018 34

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ полного дифференциала функции ДВУХ ПЕРЕМЕННЫХ. Пусть S – поверхность, P 0 – фиксированная точка на поверхности S, P – текущая точка на поверхности S. Проведем секущую прямую PP 0. Плоскость, проходящая через точку P 0, называется касательной плоскостью к поверхности S в точке P 0, если угол между секущей PP и этой плоскостью стремится к 0 нулю когда точка P стремится к P 0 , двигаясь по поверхности S произвольным образом. 1/21/2018 35

Прямая, проходящая через точку P перпендикулярно касатель- 0 ной плоскости к поверхности в этой точке, называется нормалью к поверхности в точке P 0. 1) если функция z = f(x, y) дифференцируема в точке M 0 (x 0 , y 0 ), то поверхность z = f ( x , y ) имеет в точке P 0 ( x касательную плоскость. Уравнение касательной плоскости : уравнение нормали к поверхности z = f(x, y) в P 0(x 0, y 0, f(x 0, y 0)): 1/21/2018 36

2) если поверхность задана уравнением F(x, y, z) = 0 -неявно, F(x, y, z) – дифференцируема в P 0(x 0, y 0, z 0), причем хотя бы одна из ее частных производных не обращается в P 0 в ноль, то касательная плоскость к поверхности в точке P 0(x 0, y 0, z 0) существует и ее уравнение уравнения нормали к поверхности F(x, y, z) = 0 в P 0(x 0, y 0, z 0): ü Замечание Точка P 0(x 0, y 0, z 0) поверхности F(x, y, z) = 0, в которой все частные производные функции F ( x , y , z ) обращаются в ноль, называется особой точкой поверхности. 1/21/2018 37

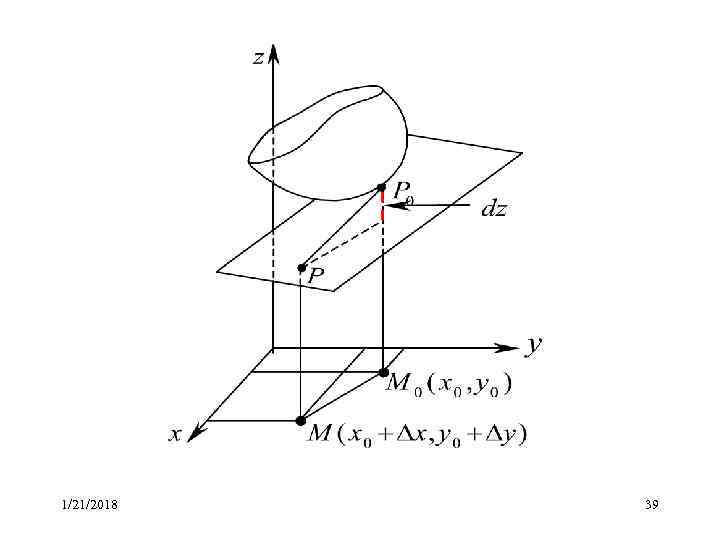
Полный дифференциал функции z = f ( x , y ) в точке M 0 ( x 0 , y равен приращению, которое получает аппликата точки P 0 ( x 0 , y 0 , f ( x 0 , y 0 )) касательной плоскости z = f ( x , y ), когда ее координаты x 0 и y 0 получаю приращения x и y соответственно. 1/21/2018 38

1/21/2018 39

Очевидно, что соответствие ( x 0 , y 0 , x , y ) df ( x 0 , функцией (четырех переменных). Ее называют полным дифференциалом функции z = f(x, y) и обозначают dz или df(x, y). Полный дифференциал функции n переменных обладает теми же свойствами, что и дифференциал функции одной переменной. В частности, для df(x, y) существует вторая, инвариантная форма записи: 1/21/2018 40

Теорема о дифференцируемости функции • Если z = f(x; y) имеет непрерывные частные производные и • то функция z = f ( x ; y ) дифференцируемой в точке (х; у). Главная часть приращения функции линейная относительно приращения аргументов называется полным дифференциалом функции z = f(x; y) и обозначается: 1/21/2018 41

Дифференциалы высших порядков ФНП Пусть z = f(x, y) дифференцируема в области D 1 D(f). Ее дифференциал dz(M) – функция переменных x, y, dx, dy. Далее будем dz(M) называть дифференциалом 1 -го порядка. Зафиксируем значение dx и dy. Тогда dz(M) станет функцией двух переменных x и y. Дифференциал функции dz(M) (если он существует) называется дифференциалом 2 - го порядка функции z = f ( x , y ) (или вто - рым дифференциалом функции z = f(x, y)) и обозначается d 2 z, d 2 f(x, y). Дифференциал функции d 2 z(M) (если он существует) называют дифференциалом третьего порядка функции z = f ( x , y ) обозначается d 3 z, d 3 f(x, y). 1/21/2018 42

Продолжая далее этот процесс, определим дифференциал n -го порядка функции z = f ( x , y ) как дифференциал от ее диффе ренциала порядка n – 1. Обозначают: d nz, d nf(x, y). ü Замечание Значение дифференциала n -го порядка функции f(x, y) в точке (x 0, y 0) обозначают d nz(M 0), d nf (x 0, y 0). Дифференциалы порядка n > 1 называют дифференциалами высших порядков. Если функция z = f ( x , y ) имеет дифференциал порядка n , то е называют n раз дифференцируемой. ТЕОРЕМА (о связи дифференциала n-го порядка и n-х частных производных). Если все производные k-го порядка функции z = f(x, y) в области D непрерывны, то она k раз дифференцируема. При этом имеет место символическая формула 1/21/2018 43

ü Замечание 1) Например, для n = 2 получим: Для n = 3 получим: 44

Частные производные сложных ФНП Пусть z = f(x, y), где x = 1(u, v), y = 2(u, v). Тогда z – сложная функция независимых переменных u и v. ТЕОРЕМА ( о производной сложной функции). Пусть z = f(x, y), где x = 1(u, v), y = 2(u, v). Если f(x, y), 1(u, v), 2(u, v) дифференцируемы, то справедливы формулы 1/21/2018 45

ЧАСТНЫЕ СЛУЧАИ сложной ФНП 1) Пусть z = f(x, y), где x = 1(t), y = 2(t). Тогда z – сложная функцией одной переменной t. Если f(x, y), 1(t), 2(t) дифференцируемы, то справедлива формула 2) Пусть z = f(x, y), где y = (x) Тогда z – сложная функцией одной переменной x. Если f(x, y), (x) дифференцируемы, то справедлива формула Производная в левой части формулы называется полной производной функции z. 1/21/2018 46

Частные производные неявно заданной функции. 1) уравнение F(x, y) = 0 определяет в некоторой окрестности U точки x 0, непрерывную функцию y = f(x). 2) Тогда 1/21/2018 47

Экстремумы ФНП ФНП Пусть z = f(x, y) определена в некоторой области D x. Oy , M 0(x 0, y 0) D. ОПРЕДЕЛЕНИЕ Точка M максимума функции f ( x , y ) , если M выполняется неравенство f(x, y) f(x 0, y 0). Точка M 0(x 0, y 0) называется точкой минимума функции f(x, y), если M(x, y) U(M 0, ) выполняется неравенство f(x, y) f(x 0, y 0). Точки максимума и минимума функции называются ее точками экстремума. 1/21/2018 48

ü Замечания 1) По смыслу точкой максимума (минимума) функции f ( x , y ) могут быть только внутренние точки области D. 2) Понятия экстремумов носят локальный характер. 3) В рассматриваемой области функция может совсем не иметь экстремумов, 4) может иметь несколько (в том числе бесчисленно много) минимумов и максимумов. 5) При этом некоторые минимумы могут оказаться больше некоторых ее максимумов. 1/21/2018 49

ТЕОРЕМА (необходимые условия экстремума). Если функция z = f(x, y) в точке M 0(x 0, y 0) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю, либо хотя бы одна из них не существует. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ теоремы . Если M 0(x 0, y 0) – точка экстремума функции z = f(x, y), то касательная плоскость к графику этой функции в точке P 0 ( x 0 , y 0 , f ( x 0 , y 0 )) либо параллельна плоскости x. Oy , вообще не существует. Точки, удовлетворяющие условиям теоремы, называются критическими точками функции z = f(x, y). 1/21/2018 50

ТЕОРЕМА (достаточные условия экстремума) Пусть M 0(x 0, y 0) – критическая точка функции z = f(x, y) и в некоторой окрестности точки M 0 функция имеет непрерывные частные производные до 2 - го порядка включительно. Обозначим Тогда 1) если A C – B 2 < 0 , то точка M 0(x 0, y 0) не является точкой экстремума; 2) если A C – B 2 > 0 и A > 0 , то в точке M 0(x 0, y 0) функция имеет минимум; 3) если A C – B 2 > 0 и A < 0 , то в точке M 0(x 0, y 0) функция имеет максимум; 4) если A C – B 2 = 0 , то никакого заключения о крити- ческой точке M 0(x 0, y 0) сделать нельзя и требуются дополнительные исследования. 1/21/2018 51

• Замечание Квадратичная форма легко запоминается, если записать её в виде определителя: в точке (x 0, y 0) есть экстремум экстремума нет. 1/21/2018 52

ü Замечание 1) Если исследовать критическую точку M 0 ( x 0 , y 0 ) не удалось, то ответ на вопрос о наличии в M 0 экстремума даст знак f(x 0, y 0) : а) если при всех достаточно малых x и y имеем f(x 0, y 0) < 0, то M 0(x 0, y 0) – точка строгого максимума; б) если при всех достаточно малых x и y имеем f(x 0, y 0) > 0, то M 0(x 0, y 0) – точка строгого минимума. ü Замечание В случае нестрогих экстремумов при некоторых значениях x и y приращение функции будет нулевым 1/21/2018 53

Пример Исследовать на u = x 2 + 2 y 2 +x. экстремум функцию Решение • Находим частные Критической для данной производные первого функции будет точка . порядка и приравниваем их к нулю: Вычисляем значения А, В, и С в этой точке: Значит, в точке имеет экстремум. Так как A = 2 > 0, то в место этой точке функция достигает минимума 1/21/2018 54

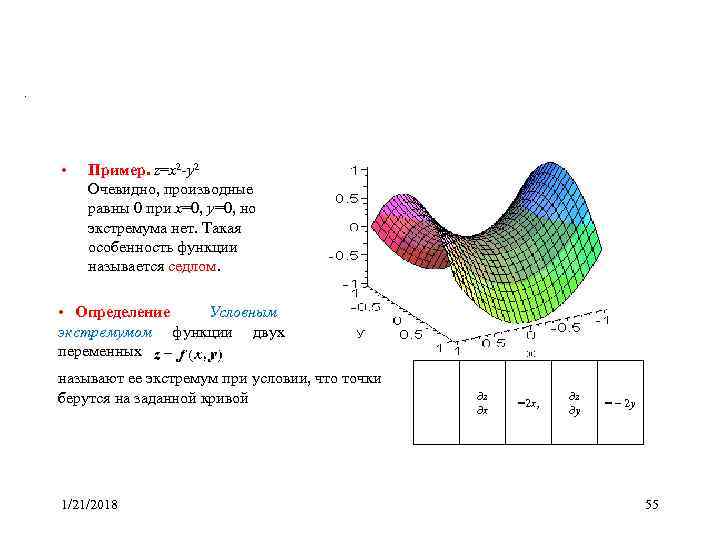
. • Пример. z=x 2 -y 2 Очевидно, производные равны 0 при x=0, y=0, но экстремума нет. Такая особенность функции называется седлом. • Определение Условным экстремумом функции двух переменных называют ее экстремум при условии, что точки берутся на заданной кривой z =2 x, = - 2 y x y 1/21/2018 55

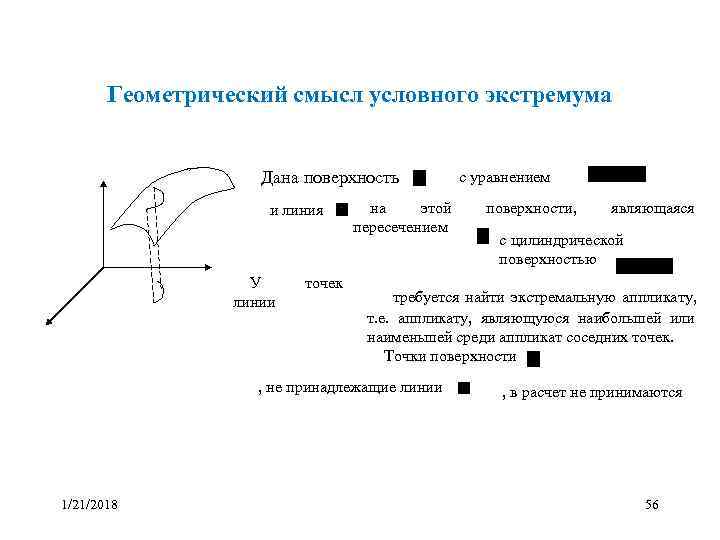
Геометрический смысл условного экстремума Дана поверхность с уравнением и линия на этой поверхности, являющаяся пересечением с цилиндрической поверхностью У точек линии требуется найти экстремальную аппликату, т. е. аппликату, являющуюся наибольшей или наименьшей среди аппликат соседних точек. Точки поверхности , не принадлежащие линии , в расчет не принимаются 1/21/2018 56

. Необходимое условие условного экстремума функции в точке число называется множителем Лагранжа, - критическая точка функции при наложении условия Критическая точка может оказаться точкой условного экстремума, но не обязательно каждая 1/21/2018 (условие не достаточное). 57

Достаточное условие для условного экстремума в критической точке Если то критическая тоска – точка условного минимума, если - точка условного максимума 1/21/2018 58